人教版数学八年级上册12.2.4 直角三角形全等的判定“HL”课件(共17张)
文档属性
| 名称 | 人教版数学八年级上册12.2.4 直角三角形全等的判定“HL”课件(共17张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-23 00:00:00 | ||
图片预览



文档简介
直角三角形全等的判定“HL”
学习任务
据以往所学的判定方法,两个直角三角形需具备怎样的条件才能够全等?
斜边和一条直角边分别相等的两个直角三角形全等吗?
知识精讲
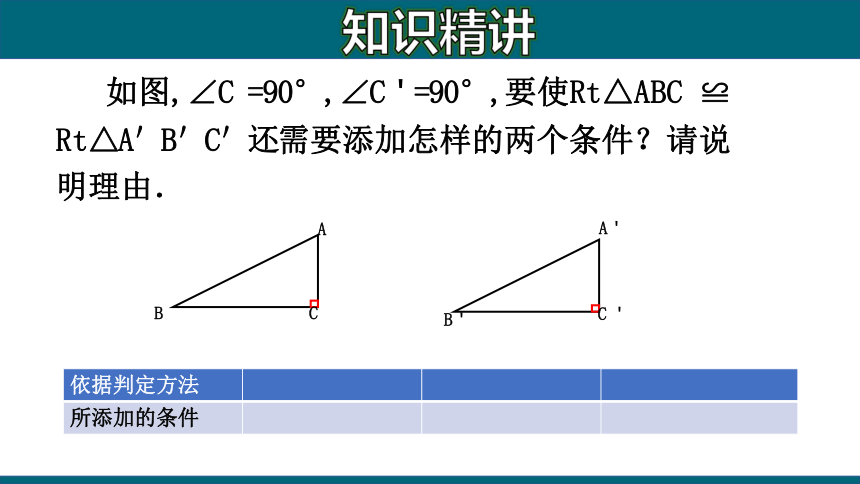
如图,∠C =90°,∠C'=90°,要使Rt△ABC ≌ Rt△A'B'C'还需要添加怎样的两个条件?请说明理由.
C
B
A
A '
B '
C '
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}依据判定方法
所添加的条件
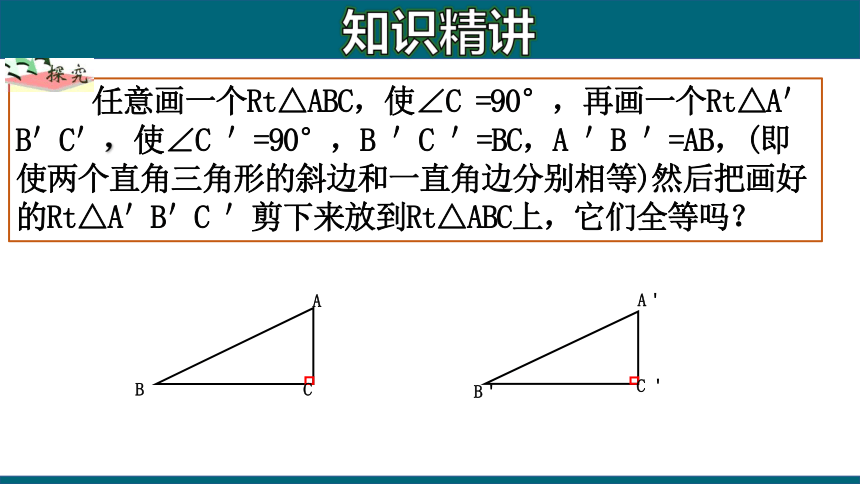
任意画一个Rt△ABC,使∠C =90°,再画一个Rt△A'B'C',使∠C '=90°,B 'C '=BC,A 'B '=AB,(即使两个直角三角形的斜边和一直角边分别相等)然后把画好的Rt△A'B'C '剪下来放到Rt△ABC上,它们全等吗?
知识精讲
C
B
A
A '
B '
C '
知识精讲
C ′
N
M
A
B
C
A ′
B ′
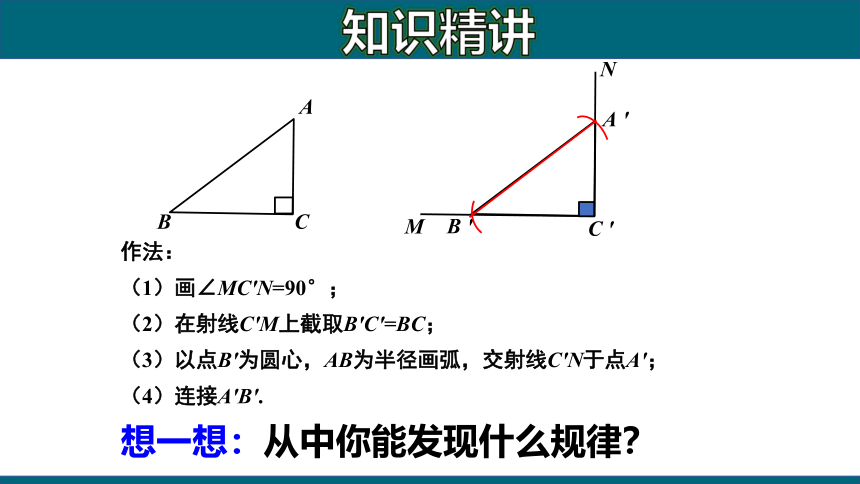
作法:
(1)画∠MC'N=90°;
(2)在射线C'M上截取B'C'=BC;
(3)以点B'为圆心,AB为半径画弧,交射线C'N于点A';
(4)连接A'B'.
想一想:从中你能发现什么规律?
知识精讲
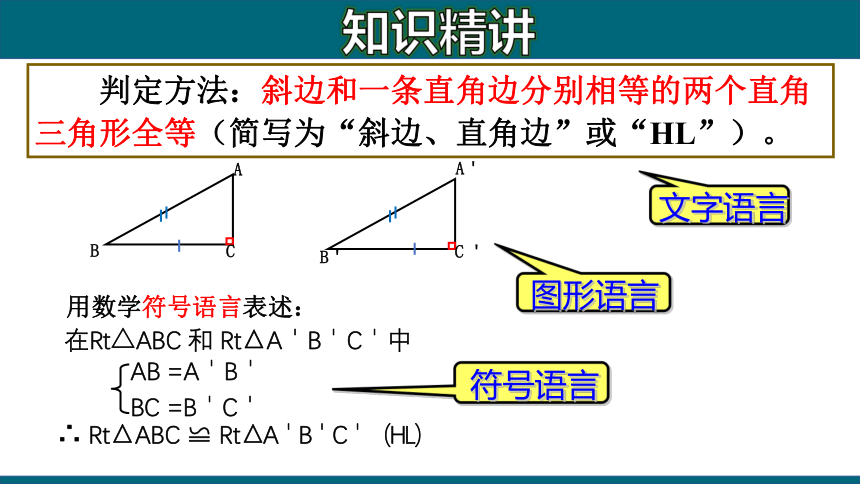
判定方法:斜边和一条直角边分别相等的两个直角三角形全等(简写为“斜边、直角边”或“HL”)。
用数学符号语言表述:
在Rt△ABC 和 Rt△A'B'C'中
∴ Rt△ABC ≌ Rt△A'B'C'(HL)
AB =A'B'
BC =B'C'
文字语言
符号语言
图形语言
C
B
A
A '
B '
C '
如图,∠C =90°,∠C ′=90°,A C=A′ C ′,B C=B ′C ′,
求证:△ABC ≌ △A′B′C′
C
B
A
A'
B'
C'
解:在Rt△ABC 和 Rt△A'B'C'中
∴ Rt△ABC ≌ Rt△A'B'C'(HL)
AC =A′C′
BC =B′C′
解:在△ABC 和△ A′B′ C′中
∴ △ABC ≌△ A′B′ C′(SAS).
AC= A′C′
∠C =∠C′
BC =B′C′
下面两种解法哪个是正确的?
方法一:
方法二:
典例解析
证明: ∵ AC⊥BC, BD⊥AD,
∴∠C与∠D都是直角.
AB=BA,
AC=BD .
在 Rt△ABC 和Rt△BAD 中,
∴ Rt△ABC≌Rt△BAD (HL).
∴ BC﹦AD(全等三角形的对应边相等).
A
B
D
C
应用“HL”的前提条件是在直角三角形中.
这是应用“HL”判定方法的书写格式.
利用全等证明两条线段相等,这是常见的思路.
如图,AC⊥BC, BD⊥AD, AC﹦BD,求证:BC﹦AD。
典例解析
如图,AC、BD相交于点P,AC⊥BC,BD⊥AD,垂足分别为C、D,AD=BC.求证:AC=BD.
变式1
HL
AC=BD
Rt△ABD≌Rt△BAC
典例解析
典例解析
如图:AB⊥AD,CD⊥BC,AB=CD,判断AD和BC
的位置关系.
变式2
HL
∠ADB=∠CBD
Rt△ABD≌Rt△CDB
AD∥BC
2、判断满足下列条件的两个直角三角形是否全等,不全等的画“×”,全等的注明理由:
(1)一个锐角和这个角的对边对应相等;( )
(2)一个锐角和这个角的邻边对应相等;( )
(3)一个锐角和斜边对应相等; ( )
(4)两直角边对应相等; ( )
(5)一条直角边和斜边对应相等 ( )
HL
×
SAS
AAS
AAS
巩固训练
3、如图,C 是路段AB 的中点,两人从C 同时出发,以相同的速度分别沿两条直线行走,并同时到达D,E 两地.DA⊥AB,EB⊥AB. D,E 与路段AB的距离相等吗?为什么?
A
B
C
D
E
巩固训练
C
5、如图,AB =CD,AE⊥BC,DF⊥BC,垂足分别为E ,F,CE=BF.求证:AE =DF.
A
B
C
D
E
F
巩固训练
实际应用
A
小结梳理
1
在直角三角形中我们会区别并正确运用各种判定方法
2
判定方法:斜边和一条直角边分别相等的两个直角三角形全等
学习任务
据以往所学的判定方法,两个直角三角形需具备怎样的条件才能够全等?
斜边和一条直角边分别相等的两个直角三角形全等吗?
知识精讲
如图,∠C =90°,∠C'=90°,要使Rt△ABC ≌ Rt△A'B'C'还需要添加怎样的两个条件?请说明理由.
C
B
A
A '
B '
C '
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}依据判定方法
所添加的条件
任意画一个Rt△ABC,使∠C =90°,再画一个Rt△A'B'C',使∠C '=90°,B 'C '=BC,A 'B '=AB,(即使两个直角三角形的斜边和一直角边分别相等)然后把画好的Rt△A'B'C '剪下来放到Rt△ABC上,它们全等吗?
知识精讲
C
B
A
A '
B '
C '
知识精讲
C ′
N
M
A
B
C
A ′
B ′
作法:
(1)画∠MC'N=90°;
(2)在射线C'M上截取B'C'=BC;
(3)以点B'为圆心,AB为半径画弧,交射线C'N于点A';
(4)连接A'B'.
想一想:从中你能发现什么规律?
知识精讲
判定方法:斜边和一条直角边分别相等的两个直角三角形全等(简写为“斜边、直角边”或“HL”)。
用数学符号语言表述:
在Rt△ABC 和 Rt△A'B'C'中
∴ Rt△ABC ≌ Rt△A'B'C'(HL)
AB =A'B'
BC =B'C'
文字语言
符号语言
图形语言
C
B
A
A '
B '
C '
如图,∠C =90°,∠C ′=90°,A C=A′ C ′,B C=B ′C ′,
求证:△ABC ≌ △A′B′C′
C
B
A
A'
B'
C'
解:在Rt△ABC 和 Rt△A'B'C'中
∴ Rt△ABC ≌ Rt△A'B'C'(HL)
AC =A′C′
BC =B′C′
解:在△ABC 和△ A′B′ C′中
∴ △ABC ≌△ A′B′ C′(SAS).
AC= A′C′
∠C =∠C′
BC =B′C′
下面两种解法哪个是正确的?
方法一:
方法二:
典例解析
证明: ∵ AC⊥BC, BD⊥AD,
∴∠C与∠D都是直角.
AB=BA,
AC=BD .
在 Rt△ABC 和Rt△BAD 中,
∴ Rt△ABC≌Rt△BAD (HL).
∴ BC﹦AD(全等三角形的对应边相等).
A
B
D
C
应用“HL”的前提条件是在直角三角形中.
这是应用“HL”判定方法的书写格式.
利用全等证明两条线段相等,这是常见的思路.
如图,AC⊥BC, BD⊥AD, AC﹦BD,求证:BC﹦AD。
典例解析
如图,AC、BD相交于点P,AC⊥BC,BD⊥AD,垂足分别为C、D,AD=BC.求证:AC=BD.
变式1
HL
AC=BD
Rt△ABD≌Rt△BAC
典例解析
典例解析
如图:AB⊥AD,CD⊥BC,AB=CD,判断AD和BC
的位置关系.
变式2
HL
∠ADB=∠CBD
Rt△ABD≌Rt△CDB
AD∥BC
2、判断满足下列条件的两个直角三角形是否全等,不全等的画“×”,全等的注明理由:
(1)一个锐角和这个角的对边对应相等;( )
(2)一个锐角和这个角的邻边对应相等;( )
(3)一个锐角和斜边对应相等; ( )
(4)两直角边对应相等; ( )
(5)一条直角边和斜边对应相等 ( )
HL
×
SAS
AAS
AAS
巩固训练
3、如图,C 是路段AB 的中点,两人从C 同时出发,以相同的速度分别沿两条直线行走,并同时到达D,E 两地.DA⊥AB,EB⊥AB. D,E 与路段AB的距离相等吗?为什么?
A
B
C
D
E
巩固训练
C
5、如图,AB =CD,AE⊥BC,DF⊥BC,垂足分别为E ,F,CE=BF.求证:AE =DF.
A
B
C
D
E
F
巩固训练
实际应用
A
小结梳理
1
在直角三角形中我们会区别并正确运用各种判定方法
2
判定方法:斜边和一条直角边分别相等的两个直角三角形全等
