人教版数学八年级上册12.2.3 全等三角形的判定㈢“AAS”“ASA课件(共21张PPT)
文档属性
| 名称 | 人教版数学八年级上册12.2.3 全等三角形的判定㈢“AAS”“ASA课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-23 14:31:44 | ||
图片预览


文档简介
全等三角形的判定㈢“AAS”“ASA”
学习目标
已知三角形的两角和一边,有哪几种可能的情况?
已知两个三角形的两角和一边分别相等,能否判断两个三角形全等?
知识精讲
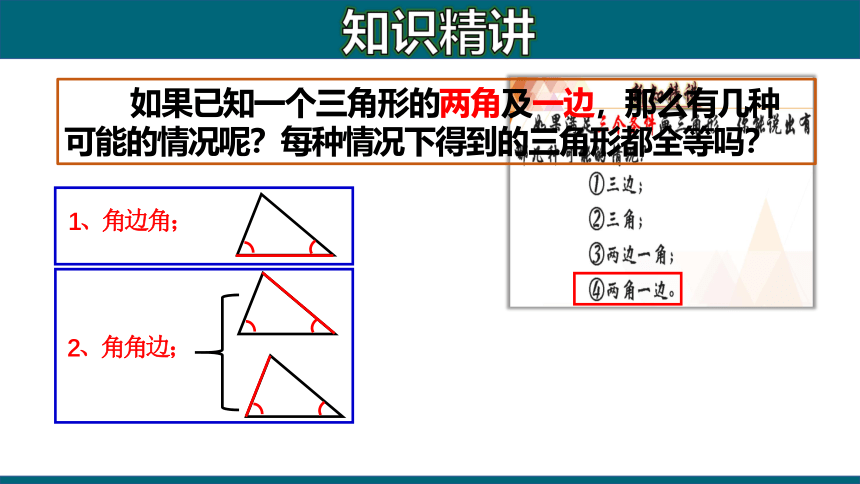
如果已知一个三角形的两角及一边,那么有几种可能的情况呢?每种情况下得到的三角形都全等吗?
1、角边角;
2、角角边;
知识精讲
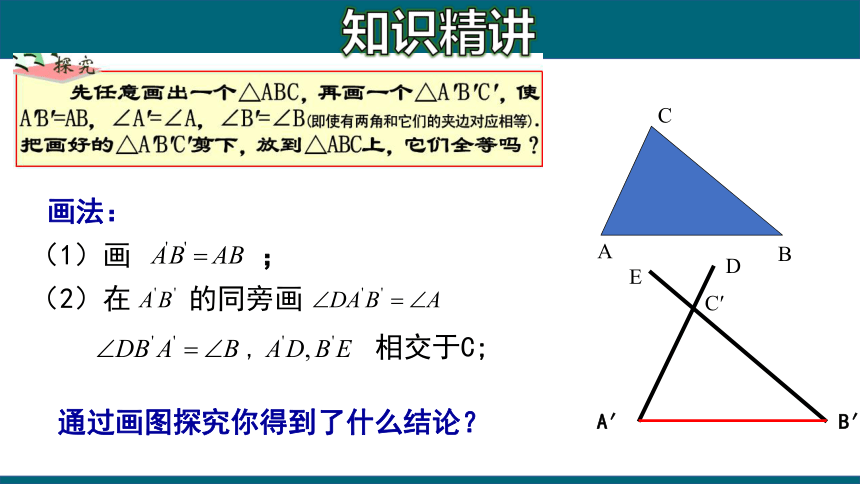
画法:
(1)画 ;
(2)在 的同旁画
, 相交于C;
通过画图探究你得到了什么结论?
C′
C
A
B
B′
A′
E
D
知识精讲
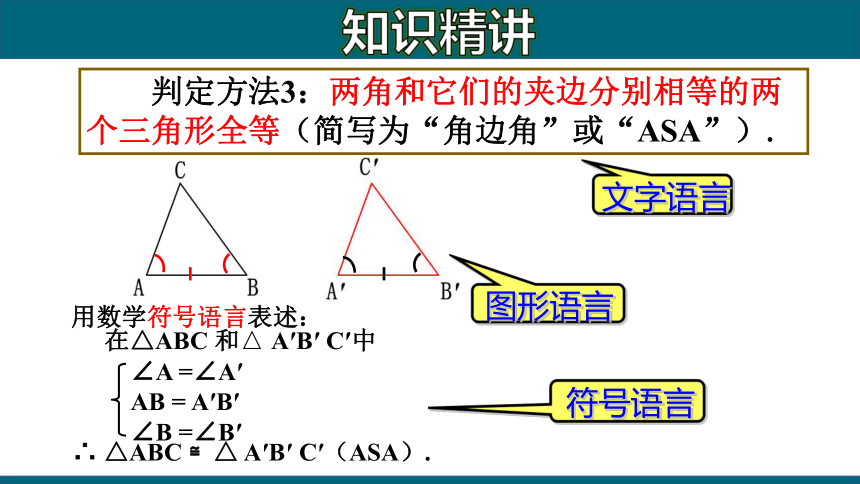
判定方法3:两角和它们的夹边分别相等的两个三角形全等(简写为“角边角”或“ASA”).
用数学符号语言表述:
在△ABC 和△ A′B′ C′中
∴ △ABC ≌△ A′B′ C′(ASA).
∠A =∠A′
AB = A′B′
∠B =∠B′
文字语言
符号语言
图形语言
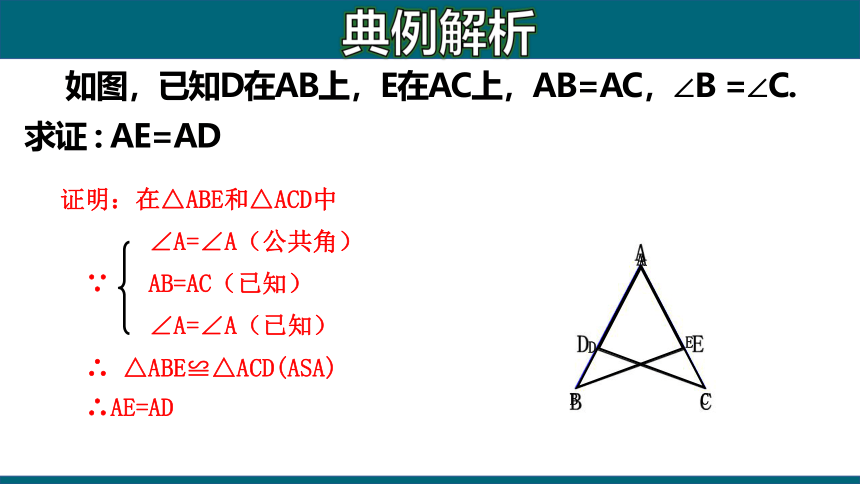
如图,已知D在AB上,E在AC上,AB=AC,∠B =∠C.
求证 : AE=AD
A
E
B
A
D
C
证明:在△ABE和△ACD中
∠A=∠A(公共角)
∵ AB=AC(已知)
∠A=∠A(已知)
∴ △ABE≌△ACD(ASA)
∴AE=AD
典例解析
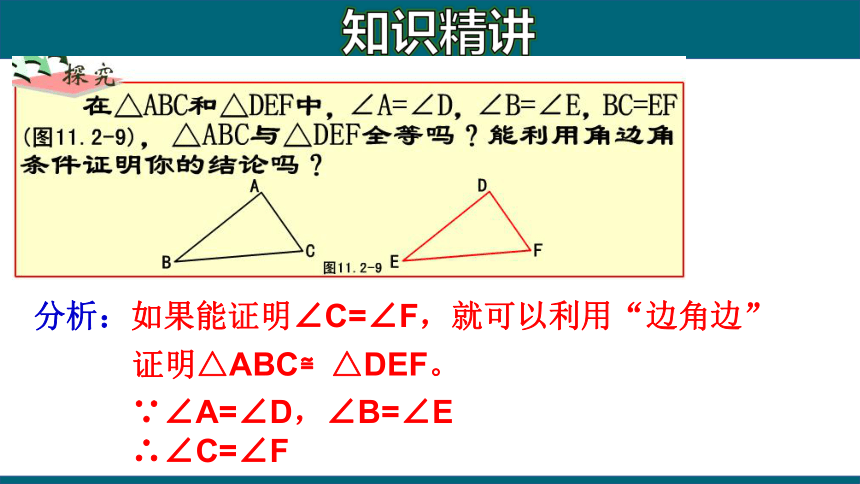
知识精讲
分析:如果能证明∠C=∠F,就可以利用“边角边”
证明△ABC≌△DEF。
∵∠A=∠D,∠B=∠E
∴∠C=∠F
知识精讲
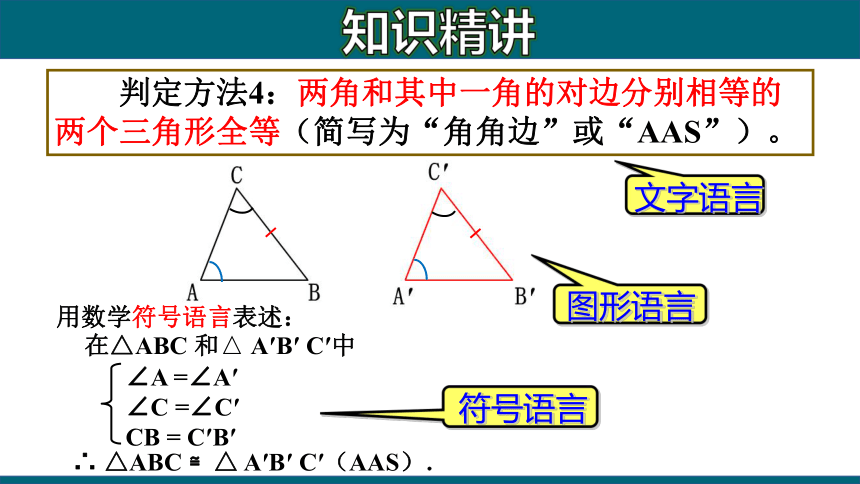
判定方法4:两角和其中一角的对边分别相等的两个三角形全等(简写为“角角边”或“AAS”)。
用数学符号语言表述:
在△ABC 和△ A′B′ C′中
∴ △ABC ≌△ A′B′ C′(AAS).
∠A =∠A′
∠C =∠C′
CB = C′B′
文字语言
符号语言
图形语言
典例解析
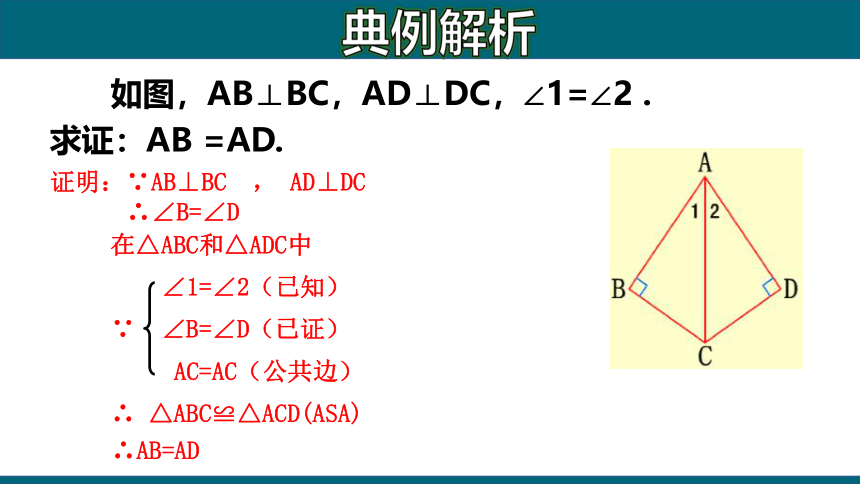
如图,AB⊥BC,AD⊥DC,∠1=∠2 .求证:AB =AD.
在△ABC和△ADC中
∠1=∠2(已知)
∵ ∠B=∠D(已证)
AC=AC(公共边)
∴ △ABC≌△ACD(ASA)
∴AB=AD
证明:∵AB⊥BC , AD⊥DC
∴∠B=∠D
巩固训练
1、如图,已知AB与CD相交于点O,AC=BD,由"AAS"得到△AOC≌△BOD.则需添加的一个条件是:____________ .
A
O
B
C
D
∠A=∠B或∠C=∠D
2、已知: △ABC和△ A′B′C′中,AB=A′B′,
∠A=∠A′,∠B=∠B′, 则△ABC≌△ A′B′C′
的根据是( )
A: SAS B: ASA C: AAS D:都不对
B
巩固训练
3、已知: △ABC和△A′B′C ′中,AB=A′B′,
∠A=∠A′, 若△ABC≌△ A′B′C′,
还需要什么条件( )
A:∠B=∠B′ B: ∠C=∠C′
C: AC=A′C′ D: A、B、C均可
D
巩固训练
4、如图,∠1=∠2,∠3=∠4,求证:AC=AB
1
2
3
4
A
B
D
C
在△ABD和△ACD中
∠1=∠2(已知)
∵ AD=AD(公共边)
∠ADB=∠ADC(已证)
∴ △ABD≌△ACD(ASA)
证明:∵ ∠3=∠4(已知)
∴ ∠ADB=∠ADC(等角的补角相等)
∴AC=AB(全等三角形对应角相等)
巩固训练
5、如图,AE⊥BE,AD⊥DC,CD =BE,∠DAB=∠EAC.
求证:AB =AC.
A
B
C
D
E
巩固训练
A
B
C
D
E
F
6、如图,E,F 在线段AC上,AD∥CB,AE =CF.
若∠B =∠D, 求证:DF =BE .
巩固训练
知识精讲
7、如图,已知E在AB上,∠1=∠2, ∠3=∠4,那么AC等于AD吗?为什么?
4
3
2
1
E
D
C
B
A
解:AC=AD
理由:在△EBC和△EBD中
∠1=∠2
∠3=∠4
EB=EB
∴ △EBC≌△EBD (AAS)
∴ BC=BD
在△ABC和△ABD中
AB=AB
∠1=∠2
BC=BD
∴ △ABC≌△ABD (SAS)
∴ AC=AD
知识精讲
8、
知识精讲
知识精讲
小结梳理
判定方法3:两角和它们的夹边分别相等的两个三角形全等(简写为“角边角”或“ASA”)。
判定方法4:两角和其中一角的对边分别相等的两个三角形全等(简写为“角角边”或“AAS”)。
学习目标
已知三角形的两角和一边,有哪几种可能的情况?
已知两个三角形的两角和一边分别相等,能否判断两个三角形全等?
知识精讲
如果已知一个三角形的两角及一边,那么有几种可能的情况呢?每种情况下得到的三角形都全等吗?
1、角边角;
2、角角边;
知识精讲
画法:
(1)画 ;
(2)在 的同旁画
, 相交于C;
通过画图探究你得到了什么结论?
C′
C
A
B
B′
A′
E
D
知识精讲
判定方法3:两角和它们的夹边分别相等的两个三角形全等(简写为“角边角”或“ASA”).
用数学符号语言表述:
在△ABC 和△ A′B′ C′中
∴ △ABC ≌△ A′B′ C′(ASA).
∠A =∠A′
AB = A′B′
∠B =∠B′
文字语言
符号语言
图形语言
如图,已知D在AB上,E在AC上,AB=AC,∠B =∠C.
求证 : AE=AD
A
E
B
A
D
C
证明:在△ABE和△ACD中
∠A=∠A(公共角)
∵ AB=AC(已知)
∠A=∠A(已知)
∴ △ABE≌△ACD(ASA)
∴AE=AD
典例解析
知识精讲
分析:如果能证明∠C=∠F,就可以利用“边角边”
证明△ABC≌△DEF。
∵∠A=∠D,∠B=∠E
∴∠C=∠F
知识精讲
判定方法4:两角和其中一角的对边分别相等的两个三角形全等(简写为“角角边”或“AAS”)。
用数学符号语言表述:
在△ABC 和△ A′B′ C′中
∴ △ABC ≌△ A′B′ C′(AAS).
∠A =∠A′
∠C =∠C′
CB = C′B′
文字语言
符号语言
图形语言
典例解析
如图,AB⊥BC,AD⊥DC,∠1=∠2 .求证:AB =AD.
在△ABC和△ADC中
∠1=∠2(已知)
∵ ∠B=∠D(已证)
AC=AC(公共边)
∴ △ABC≌△ACD(ASA)
∴AB=AD
证明:∵AB⊥BC , AD⊥DC
∴∠B=∠D
巩固训练
1、如图,已知AB与CD相交于点O,AC=BD,由"AAS"得到△AOC≌△BOD.则需添加的一个条件是:____________ .
A
O
B
C
D
∠A=∠B或∠C=∠D
2、已知: △ABC和△ A′B′C′中,AB=A′B′,
∠A=∠A′,∠B=∠B′, 则△ABC≌△ A′B′C′
的根据是( )
A: SAS B: ASA C: AAS D:都不对
B
巩固训练
3、已知: △ABC和△A′B′C ′中,AB=A′B′,
∠A=∠A′, 若△ABC≌△ A′B′C′,
还需要什么条件( )
A:∠B=∠B′ B: ∠C=∠C′
C: AC=A′C′ D: A、B、C均可
D
巩固训练
4、如图,∠1=∠2,∠3=∠4,求证:AC=AB
1
2
3
4
A
B
D
C
在△ABD和△ACD中
∠1=∠2(已知)
∵ AD=AD(公共边)
∠ADB=∠ADC(已证)
∴ △ABD≌△ACD(ASA)
证明:∵ ∠3=∠4(已知)
∴ ∠ADB=∠ADC(等角的补角相等)
∴AC=AB(全等三角形对应角相等)
巩固训练
5、如图,AE⊥BE,AD⊥DC,CD =BE,∠DAB=∠EAC.
求证:AB =AC.
A
B
C
D
E
巩固训练
A
B
C
D
E
F
6、如图,E,F 在线段AC上,AD∥CB,AE =CF.
若∠B =∠D, 求证:DF =BE .
巩固训练
知识精讲
7、如图,已知E在AB上,∠1=∠2, ∠3=∠4,那么AC等于AD吗?为什么?
4
3
2
1
E
D
C
B
A
解:AC=AD
理由:在△EBC和△EBD中
∠1=∠2
∠3=∠4
EB=EB
∴ △EBC≌△EBD (AAS)
∴ BC=BD
在△ABC和△ABD中
AB=AB
∠1=∠2
BC=BD
∴ △ABC≌△ABD (SAS)
∴ AC=AD
知识精讲
8、
知识精讲
知识精讲
小结梳理
判定方法3:两角和它们的夹边分别相等的两个三角形全等(简写为“角边角”或“ASA”)。
判定方法4:两角和其中一角的对边分别相等的两个三角形全等(简写为“角角边”或“AAS”)。
