人教版数学八年级上册12.2.1 全等三角形的判定㈠“SSS“课件(共19张PPT)
文档属性
| 名称 | 人教版数学八年级上册12.2.1 全等三角形的判定㈠“SSS“课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-23 14:35:08 | ||
图片预览


文档简介
全等三角形的判定㈠“SSS”
学习任务
探索:
两个三角形具备怎样的条件才能全等?
全等三角形判定方法“边边边”的简单应用
知识精讲
∠A =∠A′
AB =A′B′
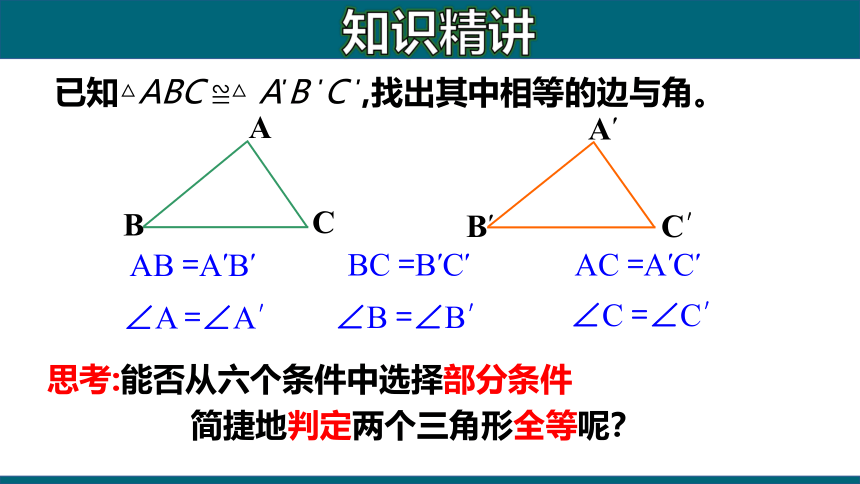
已知△ABC ≌△ A′B ′C ′,找出其中相等的边与角。
思考:能否从六个条件中选择部分条件
简捷地判定两个三角形全等呢?
A
B
C
A′
B′
C′
∠B =∠B′
BC =B′C′
∠C =∠C′
AC =A′C′
知识精讲
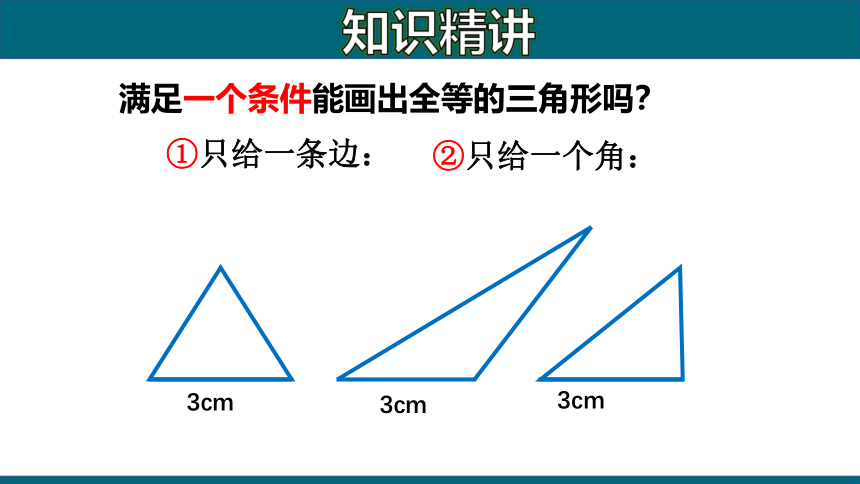
满足一个条件能画出全等的三角形吗?
3cm
3cm
3cm
①只给一条边:
②只给一个角:
知识精讲
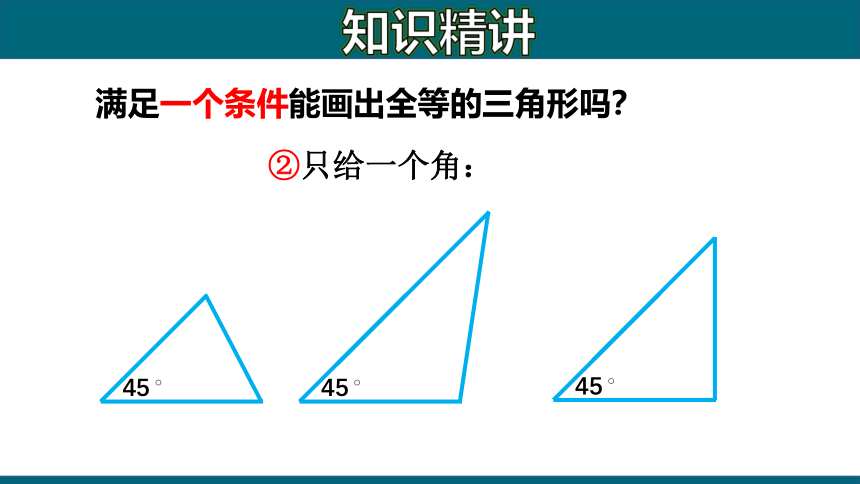
满足一个条件能画出全等的三角形吗?
45?
45?
45?
②只给一个角:
知识精讲
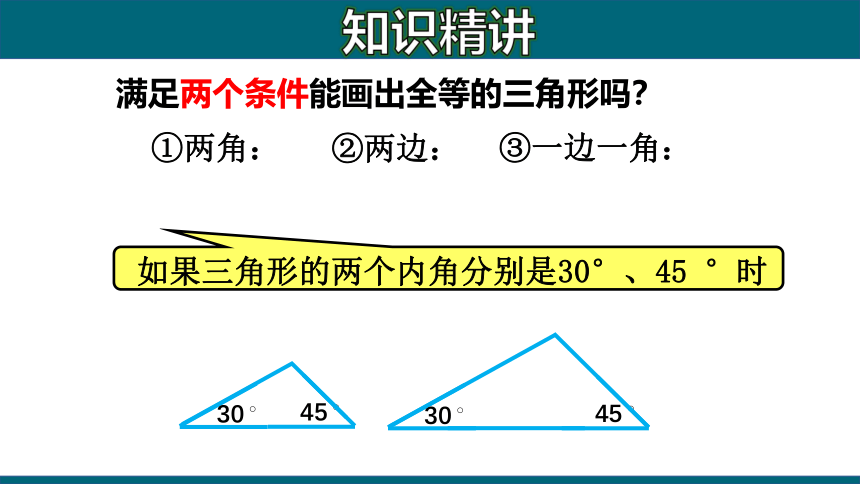
满足两个条件能画出全等的三角形吗?
①两角:
②两边:
30?
45?
30?
45?
③一边一角:
如果三角形的两个内角分别是30°、45 °时
知识精讲
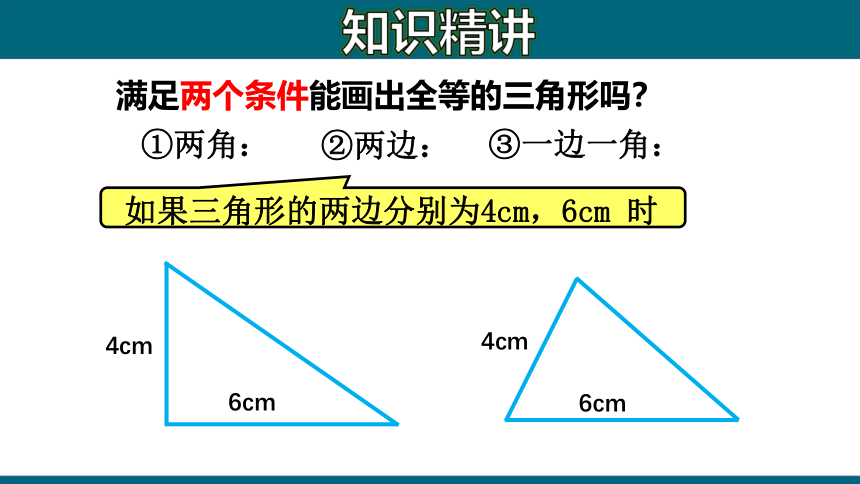
满足两个条件能画出全等的三角形吗?
①两角:
②两边:
③一边一角:
如果三角形的两边分别为4cm,6cm 时
6cm
6cm
4cm
4cm
知识精讲
只给两个条件能画出全等的三角形吗?
①两角:
②两边:
③一边一角:
三角形的一个内角为30°,一条边为4cm时
4cm
4cm
30?
30?
知识精讲
如果满足三个条件画三角形,你能说出有哪几种可能的情况?
①三边;
②三角;
③两边一角;
④两角一边。
①三边;
知识精讲
先任意画出一个△ABC,再画出一个△A′B′C′,使A′B′= AB,B′C′= BC,A′C′= AC.这两个三角形会全等吗?
知识精讲
判定方法1:三边对应相等的两个三角形全等(简写为“边边边”或“SSS”).
用数学符号语言表述:
在△ABC 和△DEF 中
∴ △ABC ≌△ DEF(SSS)
AB=DE
BC=EF
CA=FD
A
B
C
D
E
F
文字语言
符号语言
图形语言
知识精讲
例: 已知:如图,AB=AD,BC=CD,
求证:△ABC≌ △ADC
A
B
C
D
AC=
AB=
≌
∴ △ABC (SSS)
证明:在△ABC和△ADC中
(已知)
( )
(公共边)
BC=
我们把判断两个三角形全等的推理过程,
叫做证明三角形全等
典例解析
如图,已知点B,E,C,F在同一条直线上,AB=DE,AC=DF,BE=CF.
求证:(1)△ABC ≌ △DEF;
如图,已知点B,E,C,F在同一条直线上,AB=DE,AC=DF,BE=CF.
求证:(1)△ABC ≌ △DEF;
典例解析
(2)AB∥DE.
解:由(1)知△ABC≌△DEF,
所以∠B=∠DEF.
所以AB∥DE.
典例解析
巩固训练
1.如图,下列三角形中,与△ABC全等的是( )
C
2.如图,已知AB=AC,AE=AD,点B,D,E,C在同一条直线上,要利用“SSS”推理得出△ABE≌△ACD,还需要添加的一个条件可以是( )
A.BD=DE
B.BD=CE
C.DE=CE
D.以上都不对
巩固训练
小结梳理
判定方法1:三边对应相等的两个三角形全等
(简写为“边边边”或“SSS”)
1
2
全等三角形判定方法“边边边”的简单应用
学习任务
探索:
两个三角形具备怎样的条件才能全等?
全等三角形判定方法“边边边”的简单应用
知识精讲
∠A =∠A′
AB =A′B′
已知△ABC ≌△ A′B ′C ′,找出其中相等的边与角。
思考:能否从六个条件中选择部分条件
简捷地判定两个三角形全等呢?
A
B
C
A′
B′
C′
∠B =∠B′
BC =B′C′
∠C =∠C′
AC =A′C′
知识精讲
满足一个条件能画出全等的三角形吗?
3cm
3cm
3cm
①只给一条边:
②只给一个角:
知识精讲
满足一个条件能画出全等的三角形吗?
45?
45?
45?
②只给一个角:
知识精讲
满足两个条件能画出全等的三角形吗?
①两角:
②两边:
30?
45?
30?
45?
③一边一角:
如果三角形的两个内角分别是30°、45 °时
知识精讲
满足两个条件能画出全等的三角形吗?
①两角:
②两边:
③一边一角:
如果三角形的两边分别为4cm,6cm 时
6cm
6cm
4cm
4cm
知识精讲
只给两个条件能画出全等的三角形吗?
①两角:
②两边:
③一边一角:
三角形的一个内角为30°,一条边为4cm时
4cm
4cm
30?
30?
知识精讲
如果满足三个条件画三角形,你能说出有哪几种可能的情况?
①三边;
②三角;
③两边一角;
④两角一边。
①三边;
知识精讲
先任意画出一个△ABC,再画出一个△A′B′C′,使A′B′= AB,B′C′= BC,A′C′= AC.这两个三角形会全等吗?
知识精讲
判定方法1:三边对应相等的两个三角形全等(简写为“边边边”或“SSS”).
用数学符号语言表述:
在△ABC 和△DEF 中
∴ △ABC ≌△ DEF(SSS)
AB=DE
BC=EF
CA=FD
A
B
C
D
E
F
文字语言
符号语言
图形语言
知识精讲
例: 已知:如图,AB=AD,BC=CD,
求证:△ABC≌ △ADC
A
B
C
D
AC=
AB=
≌
∴ △ABC (SSS)
证明:在△ABC和△ADC中
(已知)
( )
(公共边)
BC=
我们把判断两个三角形全等的推理过程,
叫做证明三角形全等
典例解析
如图,已知点B,E,C,F在同一条直线上,AB=DE,AC=DF,BE=CF.
求证:(1)△ABC ≌ △DEF;
如图,已知点B,E,C,F在同一条直线上,AB=DE,AC=DF,BE=CF.
求证:(1)△ABC ≌ △DEF;
典例解析
(2)AB∥DE.
解:由(1)知△ABC≌△DEF,
所以∠B=∠DEF.
所以AB∥DE.
典例解析
巩固训练
1.如图,下列三角形中,与△ABC全等的是( )
C
2.如图,已知AB=AC,AE=AD,点B,D,E,C在同一条直线上,要利用“SSS”推理得出△ABE≌△ACD,还需要添加的一个条件可以是( )
A.BD=DE
B.BD=CE
C.DE=CE
D.以上都不对
巩固训练
小结梳理
判定方法1:三边对应相等的两个三角形全等
(简写为“边边边”或“SSS”)
1
2
全等三角形判定方法“边边边”的简单应用
