人教版数学八年级上册13.1.2 线段垂直平分线的性质课件(共19张PPT)
文档属性
| 名称 | 人教版数学八年级上册13.1.2 线段垂直平分线的性质课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-23 00:00:00 | ||
图片预览






文档简介
学习目标
理解并掌握线段的垂直平分线的性质.
能够运用线段的垂直平分线的性质解决实际问题.
如果一个图形沿着一条直线 ,两侧的图形能够 ,这个图形就是轴对称图形.
折痕所在的这条直线叫做_________.
对称轴
对折
完全重合
复习回顾
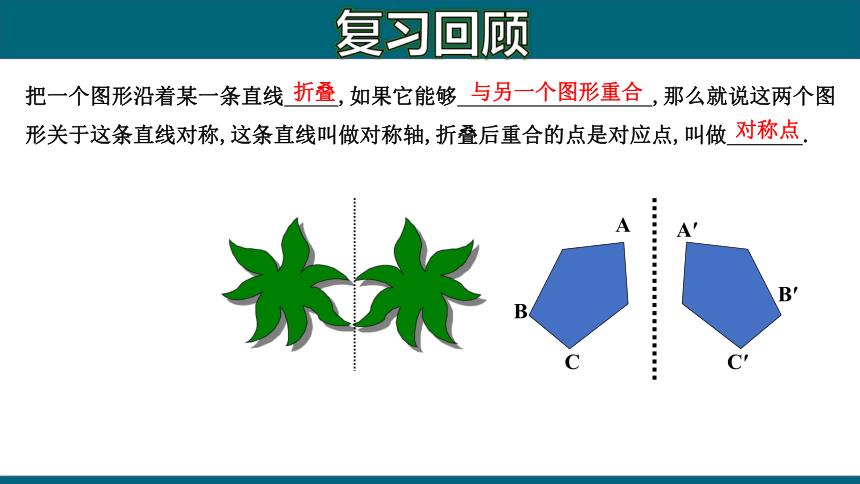
把一个图形沿着某一条直线 ,如果它能够 ,那么就说这两个图形关于这条直线对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做 .
折叠
与另一个图形重合
对称点
A′
A
B
C
B′
C′
复习回顾
D
A的对称点是F,C的对称点是_____,____的对称点是E.
能重合的点叫_________.
对称点
图中的对称点有哪些?
B
线段AF被直线m垂直且平分
直线m叫做线段AF的垂直平分线
定义:经过线段的中点且与之垂直的直线就叫这条直线的垂直平分线,也叫中垂线.
轴对称图形的对称轴,是任何一对对称点所连线段的垂直平分线.
轴对称的性质:
复习回顾
某区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问该购物中心应建于何处,才能使得它到三个小区的距离相等?
A
B
C
问题引入
如图,直线l垂直平分线段AB,P1,P2,P3,…是l 上的点,请你量一量线段P1A,P1B,P2A,P2B,P3A,P3B的长,你能发现什么?请猜想点P1,P2,P3,… 到点A 与点B 的距离之间的数量关系.
探究发现
P1A ____P1B
P2A ____ P2B
P3A ____ P3B
=
=
=
A
B
l
P1
P2
P3
知识精讲
猜想:
点P1,P2,P3,… 到点A 与点B 的距离分别相等.
命题:线段垂直平分线上的点和这条线段两个端点的距离相等.
由此你能得到什么结论?
你能验证这一结论吗?
知识精讲
已知:如图,直线l⊥AB,垂足为C,AC =CB,点P 在l 上.求证:PA =PB.
证明:∵ l⊥AB,
∴ ∠PCA =∠PCB.
又 AC =CB,PC =PC,
∴ △PCA ≌△PCB(SAS).
∴ PA =PB.
P
A
B
l
C
验证结论
知识精讲
P
A
B
l
C
线段垂直平分线上的点和这条线段两个端点的距离相等.
线段垂直平分线的性质
几何语言:
∵直线l是AB的垂直平分线,点P在直线l上,
∴PA =PB.
知识精讲
例1 如图,在△ABC中,AB=AC=20cm,DE垂直平分AB,垂足为E,交AC于D,若△DBC的周长为35cm,则BC的长为( )
A.5cm
B.10cm
C.15cm
D.17.5cm
C
解析:∵△DBC的周长为BC+BD+CD=35cm,又∵DE垂直平分AB,∴AD=BD,故BC+AD+CD=35cm.∵AC=AD+DC=20cm,
∴BC=35-20=15(cm).故选C.
【点睛】利用线段垂直平分线的性质,实现线段之间的相互转化,从而求出未知线段的长.
典例解析
1.如图①所示,直线CD是线段AB的垂直平分线,点P为直线CD上的一点,且PA=5,则线段PB的长为( )
A. 6 B. 5 C. 4 D. 3
2.如图②所示,在△ABC中,BC=8cm,边AB的垂直平分线交AB于点D,交边AC于点E, △BCE的周长等于18cm,则AC的长是 .
B
10cm
P
A
B
C
D
图①
A
B
C
D
E
图②
针对练习
例2 已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P.求证:PA=PB=PC.
B
A
C
M
N
M'
N'
P
PA=PB=PC
PB=PC
点P在线段BC的垂直平分线上
PA=PB
点P在线段AB的垂直平分线上
分析:
典例解析
证明:
∵点P在线段AB的垂直平分线MN上,
∴PA=PB.
同理 PB=PC.
∴PA=PB=PC.
结论: 三角形三边垂直平分线交于一点,这一点到三角形三个顶点的距离相等.
B
A
C
M
N
M'
N'
P
现在你能想到方法确定购物中心的位置,使得它到三个小区的距离相等吗?
典例解析
某区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问该购物中心应建于何处,才能使得它到三个小区的距离相等?
A
B
C
问题解决
例3 如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;(2)AB=BC+AD.
解析:(1)根据AD∥BC可知∠ADC=∠ECF,再根据E是CD的中点可得出△ADE≌△FCE,根据全等三角形的性质即可解答.
(2)先根据线段垂直平分线的性质得出出AB=BF,再结合(1)即可解答.
典例解析
证明:(1)∵AD∥BC,∴∠ADC=∠ECF.
∵E是CD的中点,∴DE=EC.
又∵∠AED=∠CEF,
∴△ADE≌△FCE,
∴FC=AD.
(2)∵△ADE≌△FCE,
∴AE=EF,AD=CF.
∵BE⊥AE,∴BE是线段AF的垂直平分线,
∴AB=BF=BC+CF.
∵AD=CF,
∴AB=BC+AD.
典例解析
小结梳理
P
A
B
l
C
线段垂直平分线上的点和这条线段两个端点的距离相等.
线段垂直平分线的性质
几何语言:
∵直线l是AB的垂直平分线,点P在直线l上,
∴PA =PB.
理解并掌握线段的垂直平分线的性质.
能够运用线段的垂直平分线的性质解决实际问题.
如果一个图形沿着一条直线 ,两侧的图形能够 ,这个图形就是轴对称图形.
折痕所在的这条直线叫做_________.
对称轴
对折
完全重合
复习回顾
把一个图形沿着某一条直线 ,如果它能够 ,那么就说这两个图形关于这条直线对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做 .
折叠
与另一个图形重合
对称点
A′
A
B
C
B′
C′
复习回顾
D
A的对称点是F,C的对称点是_____,____的对称点是E.
能重合的点叫_________.
对称点
图中的对称点有哪些?
B
线段AF被直线m垂直且平分
直线m叫做线段AF的垂直平分线
定义:经过线段的中点且与之垂直的直线就叫这条直线的垂直平分线,也叫中垂线.
轴对称图形的对称轴,是任何一对对称点所连线段的垂直平分线.
轴对称的性质:
复习回顾
某区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问该购物中心应建于何处,才能使得它到三个小区的距离相等?
A
B
C
问题引入
如图,直线l垂直平分线段AB,P1,P2,P3,…是l 上的点,请你量一量线段P1A,P1B,P2A,P2B,P3A,P3B的长,你能发现什么?请猜想点P1,P2,P3,… 到点A 与点B 的距离之间的数量关系.
探究发现
P1A ____P1B
P2A ____ P2B
P3A ____ P3B
=
=
=
A
B
l
P1
P2
P3
知识精讲
猜想:
点P1,P2,P3,… 到点A 与点B 的距离分别相等.
命题:线段垂直平分线上的点和这条线段两个端点的距离相等.
由此你能得到什么结论?
你能验证这一结论吗?
知识精讲
已知:如图,直线l⊥AB,垂足为C,AC =CB,点P 在l 上.求证:PA =PB.
证明:∵ l⊥AB,
∴ ∠PCA =∠PCB.
又 AC =CB,PC =PC,
∴ △PCA ≌△PCB(SAS).
∴ PA =PB.
P
A
B
l
C
验证结论
知识精讲
P
A
B
l
C
线段垂直平分线上的点和这条线段两个端点的距离相等.
线段垂直平分线的性质
几何语言:
∵直线l是AB的垂直平分线,点P在直线l上,
∴PA =PB.
知识精讲
例1 如图,在△ABC中,AB=AC=20cm,DE垂直平分AB,垂足为E,交AC于D,若△DBC的周长为35cm,则BC的长为( )
A.5cm
B.10cm
C.15cm
D.17.5cm
C
解析:∵△DBC的周长为BC+BD+CD=35cm,又∵DE垂直平分AB,∴AD=BD,故BC+AD+CD=35cm.∵AC=AD+DC=20cm,
∴BC=35-20=15(cm).故选C.
【点睛】利用线段垂直平分线的性质,实现线段之间的相互转化,从而求出未知线段的长.
典例解析
1.如图①所示,直线CD是线段AB的垂直平分线,点P为直线CD上的一点,且PA=5,则线段PB的长为( )
A. 6 B. 5 C. 4 D. 3
2.如图②所示,在△ABC中,BC=8cm,边AB的垂直平分线交AB于点D,交边AC于点E, △BCE的周长等于18cm,则AC的长是 .
B
10cm
P
A
B
C
D
图①
A
B
C
D
E
图②
针对练习
例2 已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P.求证:PA=PB=PC.
B
A
C
M
N
M'
N'
P
PA=PB=PC
PB=PC
点P在线段BC的垂直平分线上
PA=PB
点P在线段AB的垂直平分线上
分析:
典例解析
证明:
∵点P在线段AB的垂直平分线MN上,
∴PA=PB.
同理 PB=PC.
∴PA=PB=PC.
结论: 三角形三边垂直平分线交于一点,这一点到三角形三个顶点的距离相等.
B
A
C
M
N
M'
N'
P
现在你能想到方法确定购物中心的位置,使得它到三个小区的距离相等吗?
典例解析
某区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问该购物中心应建于何处,才能使得它到三个小区的距离相等?
A
B
C
问题解决
例3 如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;(2)AB=BC+AD.
解析:(1)根据AD∥BC可知∠ADC=∠ECF,再根据E是CD的中点可得出△ADE≌△FCE,根据全等三角形的性质即可解答.
(2)先根据线段垂直平分线的性质得出出AB=BF,再结合(1)即可解答.
典例解析
证明:(1)∵AD∥BC,∴∠ADC=∠ECF.
∵E是CD的中点,∴DE=EC.
又∵∠AED=∠CEF,
∴△ADE≌△FCE,
∴FC=AD.
(2)∵△ADE≌△FCE,
∴AE=EF,AD=CF.
∵BE⊥AE,∴BE是线段AF的垂直平分线,
∴AB=BF=BC+CF.
∵AD=CF,
∴AB=BC+AD.
典例解析
小结梳理
P
A
B
l
C
线段垂直平分线上的点和这条线段两个端点的距离相等.
线段垂直平分线的性质
几何语言:
∵直线l是AB的垂直平分线,点P在直线l上,
∴PA =PB.
