人教版数学八年级上册14.3.2 公式法因式分解(平方差公式)课件(共17张PPT)
文档属性
| 名称 | 人教版数学八年级上册14.3.2 公式法因式分解(平方差公式)课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1021.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-23 00:00:00 | ||
图片预览





文档简介
公式法因式分解
(平方差公式)
学习目标
会用平方差公式分解因式,能综合运用提公因式法、平方差公式进行因式分解.
通过乘法公式(a+b)(a-b)=a2-b2的逆向变形,进一步増强观察、归纳能力.
温故知新
1、什么叫把多项式分解因式?
把一个多项式化成几个整式的积的形式,叫做多项式的分解因式.
2、已学过哪一种分解因式的方法?
提公因式法
多项式(和)
因式分解
整式乘法
因式(积)
因式分解与整式乘法是互逆过程
提公因式法
温故知新
知识精讲
a
a
b
a-b
b
b
a-b
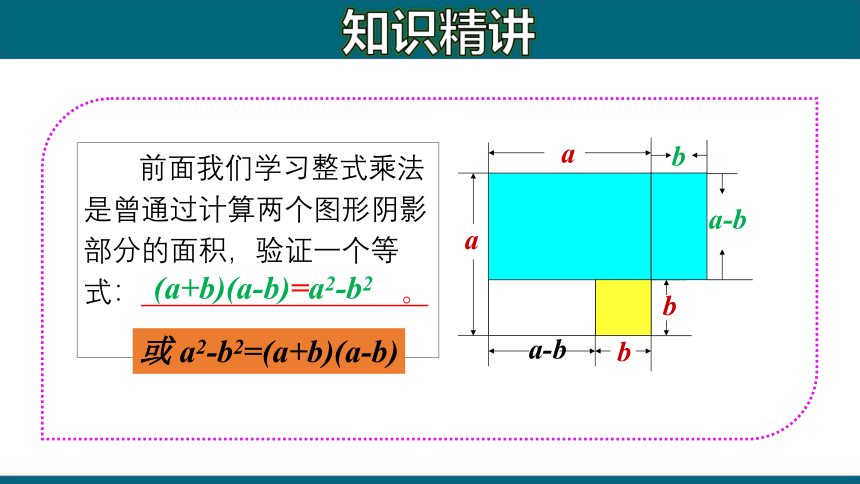
前面我们学习整式乘法是曾通过计算两个图形阴影部分的面积,验证一个等式: 。
(a+b)(a-b)=a2-b2
或 a2-b2=(a+b)(a-b)
知识精讲
整式乘法
因式分解
两个数的和与这两个数的差的积,等于这两个数的平方差。
两个数的平方差,等于这两个数的和与这两个数的差的积。
a2 - b2 = ( a + b ) ( a - b )
( a + b ) ( a - b ) = a2 - b2
平方差公式:
典例解析
例1:分解因式:
(1)4x2 - 9; (2) (x + p)2 -(x + q) 2
=(2x)2-32
a2﹣b2
=(2x+3)(2x-3)
=(a+b)(a -b)
“两个数”指的是a,b,而不是a2,b2,其中a,b可以是单项式,也可以是多项式
例1:分解因式:
(1)4x2 - 9; (2) (x + p)2 -(x + q) 2
=(2x)2-32
a2﹣b2
=(2x+3)(2x-3)
=(a+b)(a -b)
整体思想
方法总结:公式中的a、b无论表示数、单项式、还是多项式,只要被分解的多项式能转化成平方差的形式,就能用平方差公式因式分解.
典例解析
=(2m+4n)(4m+2n)
解:(1)原式=(a+b-2a)(a+b+2a)
=(b-a)(3a+b);
(2)原式=(3m+3n-m+n)(3m+3n+m-n)
=4(m+2n)(2m+n).
若用平方差公式分解后的结果中有公因式,一定要再用提公因式法继续分解.
例2 分解因式:
(1)(a+b)2-4a2; (2)9(m+n)2-(m-n)2
典例解析
例3 分解因式:
解:(1)原式=(x2)2-(y2)2
=(x2+y2)(x2-y2)
分解因式后,一定要检查是否还有能继续分解的因式,若有,则需继续分解.
=(x2+y2)(x+y)(x-y);
(2)原式=ab(a2-1)
分解因式时,一般先用提公因式法进行分解,然后再用公式法.最后进行检查.
=ab(a+1)(a-1)
典例解析
巩固训练
1.下列多项式能否用平方差公式来分解因式,为什么?
?
?
?
?
?
?
符合平方差的形式的多项式才能用平方差公式进行因式分解,即能写成: ( )2-( )2的形式.
① x2+y2
② x2-y2
③ -x2-y2
④ -x2+y2
⑤ x2-25y2
⑥ m2-1
-(x2+y2)
y2-x2
(x+5y)(x-5y)
(m+1)(m-1)
“两项、异号、平方形式”
2.下列能用平方差公式分解因式的是( )
A.a2+b2 B -a2-b2 C.a2 -c2-2ac D.-4a2+b2
3.将x2-16分解因式正确的是( )
A.(x+4)2 B.(x-4)(x+4)
C.(x+8)(x-8) D.(x-4)2+8x
B
D
巩固训练
4.分解因式:
(1)9a2-4b2; (2)x2y-4y; (3) 1-(a-b)2;
巩固训练
1.分解因式:
(4) x4-1; (5)(x+y+z)2-(x-y+z)2.
巩固训练
1.【2013年安徽12题5分】
因式分解:x2y - y= .
2.【2016年安徽12题5分】
因式分解:a3 - a= .
中考链接
小结梳理
(因式分解)
平方差公式
公式:a2 - b2 = ( a + b ) ( a - b )
特点:“两项、异号、平方形式”
一般步骤:一提、二套、三查
(平方差公式)
学习目标
会用平方差公式分解因式,能综合运用提公因式法、平方差公式进行因式分解.
通过乘法公式(a+b)(a-b)=a2-b2的逆向变形,进一步増强观察、归纳能力.
温故知新
1、什么叫把多项式分解因式?
把一个多项式化成几个整式的积的形式,叫做多项式的分解因式.
2、已学过哪一种分解因式的方法?
提公因式法
多项式(和)
因式分解
整式乘法
因式(积)
因式分解与整式乘法是互逆过程
提公因式法
温故知新
知识精讲
a
a
b
a-b
b
b
a-b
前面我们学习整式乘法是曾通过计算两个图形阴影部分的面积,验证一个等式: 。
(a+b)(a-b)=a2-b2
或 a2-b2=(a+b)(a-b)
知识精讲
整式乘法
因式分解
两个数的和与这两个数的差的积,等于这两个数的平方差。
两个数的平方差,等于这两个数的和与这两个数的差的积。
a2 - b2 = ( a + b ) ( a - b )
( a + b ) ( a - b ) = a2 - b2
平方差公式:
典例解析
例1:分解因式:
(1)4x2 - 9; (2) (x + p)2 -(x + q) 2
=(2x)2-32
a2﹣b2
=(2x+3)(2x-3)
=(a+b)(a -b)
“两个数”指的是a,b,而不是a2,b2,其中a,b可以是单项式,也可以是多项式
例1:分解因式:
(1)4x2 - 9; (2) (x + p)2 -(x + q) 2
=(2x)2-32
a2﹣b2
=(2x+3)(2x-3)
=(a+b)(a -b)
整体思想
方法总结:公式中的a、b无论表示数、单项式、还是多项式,只要被分解的多项式能转化成平方差的形式,就能用平方差公式因式分解.
典例解析
=(2m+4n)(4m+2n)
解:(1)原式=(a+b-2a)(a+b+2a)
=(b-a)(3a+b);
(2)原式=(3m+3n-m+n)(3m+3n+m-n)
=4(m+2n)(2m+n).
若用平方差公式分解后的结果中有公因式,一定要再用提公因式法继续分解.
例2 分解因式:
(1)(a+b)2-4a2; (2)9(m+n)2-(m-n)2
典例解析
例3 分解因式:
解:(1)原式=(x2)2-(y2)2
=(x2+y2)(x2-y2)
分解因式后,一定要检查是否还有能继续分解的因式,若有,则需继续分解.
=(x2+y2)(x+y)(x-y);
(2)原式=ab(a2-1)
分解因式时,一般先用提公因式法进行分解,然后再用公式法.最后进行检查.
=ab(a+1)(a-1)
典例解析
巩固训练
1.下列多项式能否用平方差公式来分解因式,为什么?
?
?
?
?
?
?
符合平方差的形式的多项式才能用平方差公式进行因式分解,即能写成: ( )2-( )2的形式.
① x2+y2
② x2-y2
③ -x2-y2
④ -x2+y2
⑤ x2-25y2
⑥ m2-1
-(x2+y2)
y2-x2
(x+5y)(x-5y)
(m+1)(m-1)
“两项、异号、平方形式”
2.下列能用平方差公式分解因式的是( )
A.a2+b2 B -a2-b2 C.a2 -c2-2ac D.-4a2+b2
3.将x2-16分解因式正确的是( )
A.(x+4)2 B.(x-4)(x+4)
C.(x+8)(x-8) D.(x-4)2+8x
B
D
巩固训练
4.分解因式:
(1)9a2-4b2; (2)x2y-4y; (3) 1-(a-b)2;
巩固训练
1.分解因式:
(4) x4-1; (5)(x+y+z)2-(x-y+z)2.
巩固训练
1.【2013年安徽12题5分】
因式分解:x2y - y= .
2.【2016年安徽12题5分】
因式分解:a3 - a= .
中考链接
小结梳理
(因式分解)
平方差公式
公式:a2 - b2 = ( a + b ) ( a - b )
特点:“两项、异号、平方形式”
一般步骤:一提、二套、三查
