人教版九年级上册数学24.1.4圆周角课件(共34张PPT)
文档属性
| 名称 | 人教版九年级上册数学24.1.4圆周角课件(共34张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-23 15:23:35 | ||
图片预览





文档简介
(共34张PPT)
圆心角、弧、弦、弦心距之间的关系
中有一组量相等,
在同圆或等圆中,
如果两个圆心角、
两条弧、
两条弦
中有一组量相等,那么它们所对应的其余各组量都分别相等
.
O
B
C
A
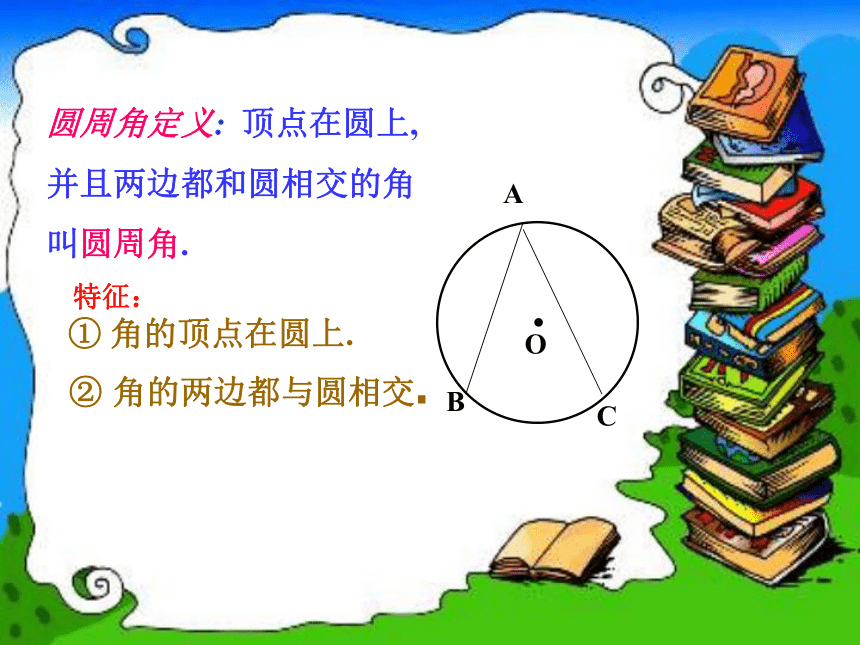
特征:
①
角的顶点在圆上.
②
角的两边都与圆相交.
圆周角定义:
顶点在圆上,
并且两边都和圆相交的角
叫圆周角.
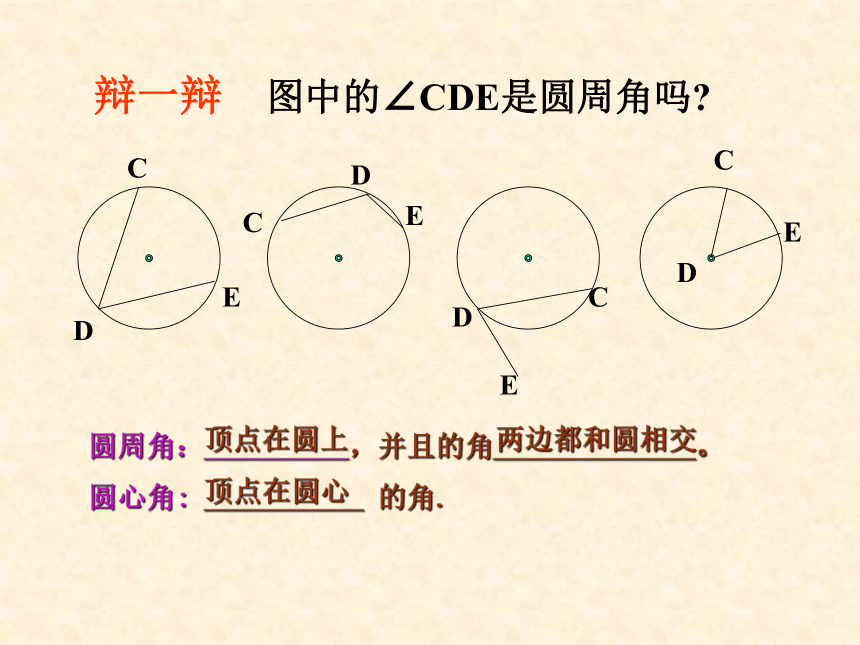
辩一辩
图中的∠CDE是圆周角吗?
C
D
E
C
D
E
C
D
E
C
D
E
圆周角:__________,并且的角______________。
圆心角:
___________
的角.
顶点在圆上
两边都和圆相交
顶点在圆心
探索:判断下列各图中,哪些是圆周角,为什么?
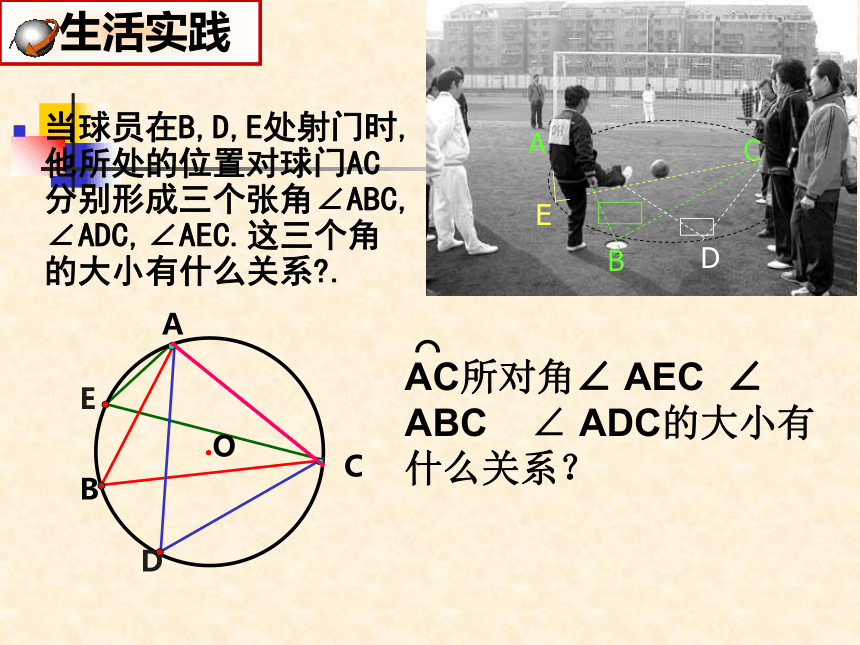
当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC,
∠ADC,∠AEC.这三个角的大小有什么关系?.
B
A
C
D
E
E
●O
B
D
C
A
AC所对角∠
AEC
∠
ABC
∠
ADC的大小有什么关系?
⌒
生活实践
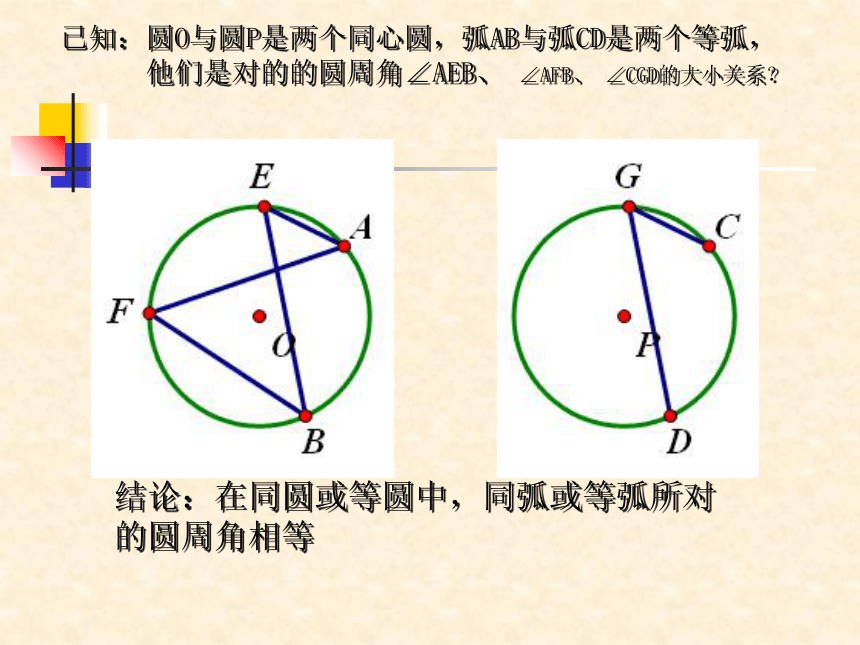
已知:圆O与圆P是两个同心圆,弧AB与弧CD是两个等弧,
他们是对的的圆周角∠AEB、
∠AFB、
∠CGD的大小关系?
结论:在同圆或等圆中,同弧或等弧所对的圆周角相等
有没有圆周角?
有没有圆心角?
它们有什么共同的特点?
它们都对着同一条弧
⌒
⌒
⌒
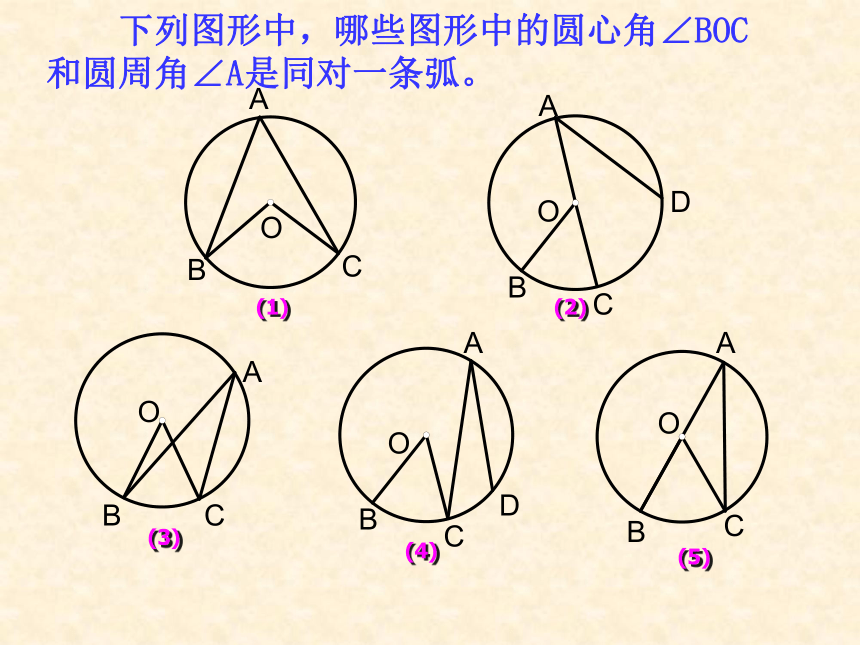
下列图形中,哪些图形中的圆心角∠BOC和圆周角∠A是同对一条弧。
(1)
(2)
(3)
(4)
(5)
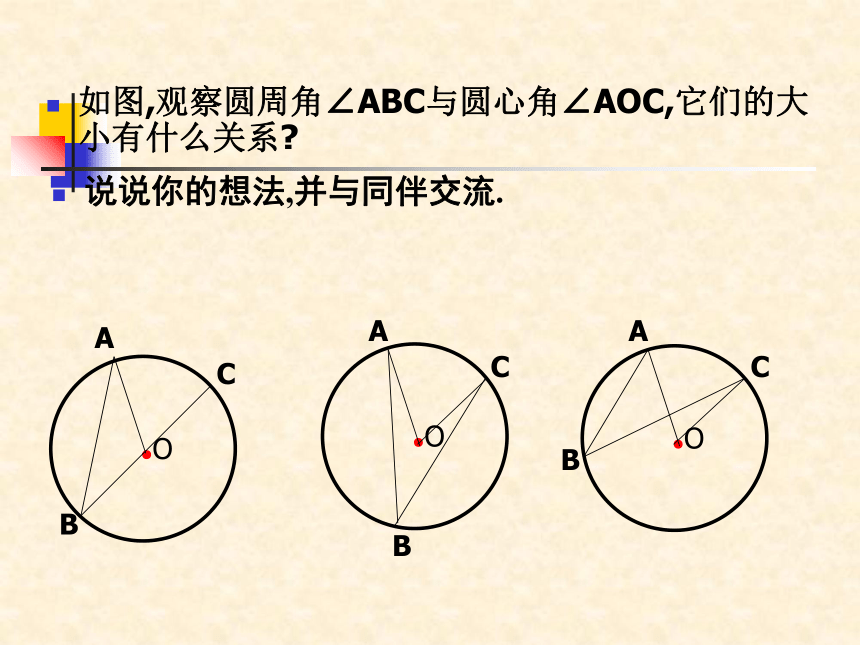
如图,观察圆周角∠ABC与圆心角∠AOC,它们的大小有什么关系?
说说你的想法,并与同伴交流.
●O
A
B
C
●O
A
B
C
●O
A
B
C
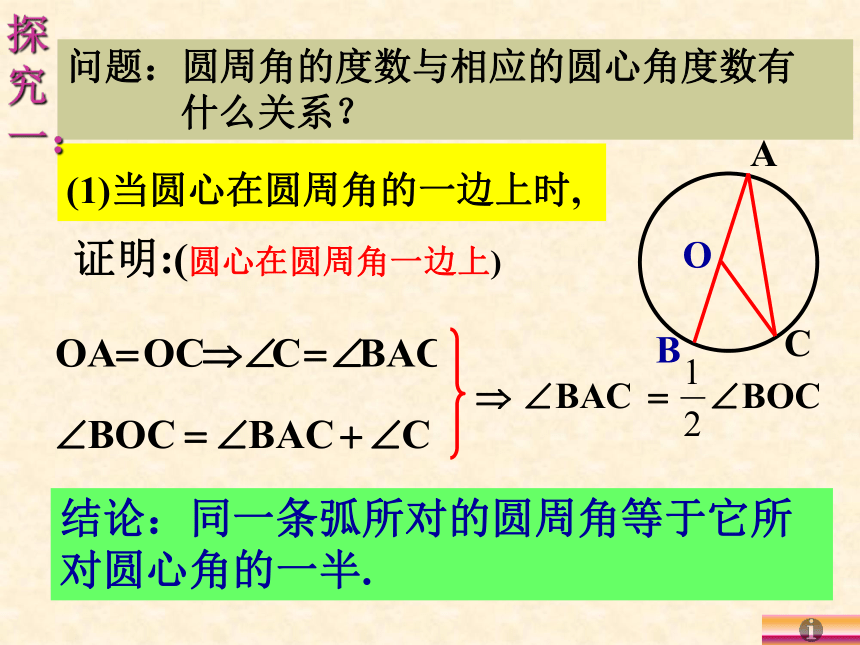
问题:圆周角的度数与相应的圆心角度数有
什么关系?
(1)当圆心在圆周角的一边上时,
探究一:
证明:(圆心在圆周角一边上)
结论:同一条弧所对的圆周角等于它所对圆心角的一半.
C
O
B
A
2.当圆心在圆周角外部时
结论:同一条弧所对的圆周角等于它所对圆心角的一半.
提示:能否转化为1的情况?
过点B作直径BD.由1可得:
∴
∠ABC
=
∠AOC.
∠ABD
=
∠AOD,∠CBD
=
∠COD,
●O
D
A
B
C
3.当圆心在圆周角内部时
提示:能否转化为1的情况?
过点B作直径BD.由1可得:
∴
∠ABC
=
∠AOC.
∠ABD
=
∠AOD,∠CBD
=
∠COD,
●O
A
B
C
D
结论:同一条弧所对的圆周角等于它所对圆心角的一半.
结论:
圆周角的定理:
在同圆或等圆中,同弧或等弧所对的圆周角
相等,都等于这条弧所对的圆心角的一半。
由圆周角定理可知:
在同圆或等圆中,如果两个圆周角相等,它们所得对的弧一定相等。
回顾:圆周角定理及推论?
思考:判断正误:
1.同弧或等弧所对的圆周角相等( )
2.相等的圆周角所对的弧相等( )
3.90°角所对的弦是直径( )
4.直径所对的角等于90°(
)
5.长等于半径的弦所对的圆周角等于30°(
)
1、如图,在⊙O中,ABC=50°,
则∠AOC等于(
)
A、50°;
B、80°;
C、90°;
D、100°
A
C
B
O
D
2、如图,△ABC是等边三角形,动点P在圆周的劣弧AB上,且不与A、B重合,则∠BPC等于(
)
A、30°;
B、60°;
C、90°;
D、45°
C
A
B
P
B
练习:
试找出下图中所有相等的圆周角。
A
B
C
D
A
B
C
O
1、如图,已知在⊙
O
中,
∠BOC
=150°,∠A=_____
2、如图,∠A是圆O的圆周角,
∠A=40°,求∠OBC的度数。
B
A
O
.
70°
x
3.求圆中角X的度数
A
O
.
X
120°
C
C
D
B
4、
如图,在直径为AB的半圆中,O为圆心,C、D为半圆上的两点,∠COD=500,则∠CAD=_________
25?
1.半圆或直径所对的圆周角等于多少度?
半圆或直径所对的圆周角是直角
。
90°的圆周角所对的弦是直径
探究二:
O
A
B
C
2.90°的圆周角所对的弦是
否是直径?
例1:如图,AB为⊙O的直径,
∠A=70°,求∠ABC的度数。
A
B
C
O
解:
∵AB为⊙O的直径
∴∠C=90°
∵
∠A=70°
∴
∠B=20
°
例2
:
如图,⊙O直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC、AD、BD的长.
又在Rt△ABD中,AD2+BD2=AB2,
解:∵AB是直径,
∴
∠ACB=
∠ADB=90°.
在Rt△ABC中,
∵CD平分∠ACB,
∴AD=BD.
1.如图AB是⊙O的直径,
C
,D是圆上的两点,若
∠ABD=40°,则∠BCD=_____.
A
B
O
C
D
40°
提示:连接AD
50°
练习
4.如图,
内接于?O,
,
AB=AC,
BD为?O的直径,
AD=6,
则AB=
.BD=_____
C
O
D
B
A
如图:圆内接四边形ABCD中,
∵
∠A的度数等于弧BCD的一
半,∠BCD的度数等于弧BAD的一半,
又∵弧BCD+弧BAD
度数为360°
∴∠A+∠C=
180°.
同理∠B+∠D=180°.
圆内接四边形的对角互补。
探究三
1、如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,
则∠BAD=
∠BCD=
反馈练习:
2、圆内接四边形ABCD中,∠A:∠B:∠C=
2:3:4,则∠A=
∠B=
∠C=
∠D=
50?
130?
60?
90?
120?
90?
3、如图,四边形ABCD内接于⊙O,
∠DCE=75?,
则∠BOD=
150?
A
B
C
D
O
A
B
C
D
E
o
4.已知⊙O中弦AB的等于半径,求弦AB所对
的圆心角和圆周角的度数.
O
A
B
圆心角为60°
圆周角为30°
或150°.
注意:一条弦所对的圆周
角有两种情况,它们的度
数之和为180度。
6.如图,圆心角∠AOB=100°,则∠ACB=___。
O
A
B
C
5、如图,AB是⊙O的直径,
若∠BCD=25°,则∠AOD=
______
130
思维拓展:
1、圆内接平行四边形一定是
形。
2、圆内接梯形一定是
形。
3、圆内接菱形一定是
形。
矩
等腰梯
正方
1._________在圆上,并且角的两边都_________的角叫做圆周角.
2.在同一圆中,一条弧所对的圆周角等于_________圆心角的_________.
3.在同圆或等圆中,____________所对的圆周角____________.
4._________所对的圆周角是直角.90°的圆周角______
是直径.
5.如图,若五边形ABCDE是⊙O的内接正五边形,则∠BOC=______,
∠ABE=______,∠ADC=______,∠ABC=______.
6.如图,若六边形ABCDEF是⊙O的内接正六边形,则∠AED=______,
∠FAE=______,∠DAB=______,∠EFA=______.
7.如图,ΔABC是⊙O的内接正三角形,若P是上一点,
则∠BPC=______;若M是上一点,则∠BMC=______.
8.在⊙O中,若圆心角∠AOB=100°,C是上一点,则∠ACB等于(
).
A.80°
B.100°
C.130°
D.140°
9.在圆中,弦AB,CD相交于E.若∠ADC=46°,∠BCD=33°,则∠DEB等于(
).
A.13°
B.79°
C.38.5°
D.101°
10.如图,AC是⊙O的直径,弦AB∥CD,若∠BAC=32°,
则∠AOD等于(
).
A.64°
B.48°
C.32°
D.76°
11.如图,弦AB,CD相交于E点,若∠BAC=27°,∠BEC=64°,
则∠AOD等于(
).
A.37°
B.74°
C.54°
D.64°
12.如图,四边形ABCD内接于⊙O,若∠BOD=138°,
则它的一个外角∠DCE等于(
).
A.69°
B.42°
C.48°
D.38°
13.如图,△ABC内接于⊙O,∠A=50°,∠ABC=60°,BD是⊙O的直径,
BD交AC于点E,连结DC,则∠AEB等于(
).
A.70°
B.90°
C.110°
D.120°
14.已知:如图,△ABC内接于⊙O,BC=12cm,∠A=60°.求⊙O的直径.
15.已知:如图,AB是⊙O的直径,弦CD⊥AB于E,∠ACD=30°,AE=2cm.求DB长.
16.已知:如图,⊙O的直径AE=10cm,∠B=∠EAC.求AC的长.
圆心角、弧、弦、弦心距之间的关系
中有一组量相等,
在同圆或等圆中,
如果两个圆心角、
两条弧、
两条弦
中有一组量相等,那么它们所对应的其余各组量都分别相等
.
O
B
C
A
特征:
①
角的顶点在圆上.
②
角的两边都与圆相交.
圆周角定义:
顶点在圆上,
并且两边都和圆相交的角
叫圆周角.
辩一辩
图中的∠CDE是圆周角吗?
C
D
E
C
D
E
C
D
E
C
D
E
圆周角:__________,并且的角______________。
圆心角:
___________
的角.
顶点在圆上
两边都和圆相交
顶点在圆心
探索:判断下列各图中,哪些是圆周角,为什么?
当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC,
∠ADC,∠AEC.这三个角的大小有什么关系?.
B
A
C
D
E
E
●O
B
D
C
A
AC所对角∠
AEC
∠
ABC
∠
ADC的大小有什么关系?
⌒
生活实践
已知:圆O与圆P是两个同心圆,弧AB与弧CD是两个等弧,
他们是对的的圆周角∠AEB、
∠AFB、
∠CGD的大小关系?
结论:在同圆或等圆中,同弧或等弧所对的圆周角相等
有没有圆周角?
有没有圆心角?
它们有什么共同的特点?
它们都对着同一条弧
⌒
⌒
⌒
下列图形中,哪些图形中的圆心角∠BOC和圆周角∠A是同对一条弧。
(1)
(2)
(3)
(4)
(5)
如图,观察圆周角∠ABC与圆心角∠AOC,它们的大小有什么关系?
说说你的想法,并与同伴交流.
●O
A
B
C
●O
A
B
C
●O
A
B
C
问题:圆周角的度数与相应的圆心角度数有
什么关系?
(1)当圆心在圆周角的一边上时,
探究一:
证明:(圆心在圆周角一边上)
结论:同一条弧所对的圆周角等于它所对圆心角的一半.
C
O
B
A
2.当圆心在圆周角外部时
结论:同一条弧所对的圆周角等于它所对圆心角的一半.
提示:能否转化为1的情况?
过点B作直径BD.由1可得:
∴
∠ABC
=
∠AOC.
∠ABD
=
∠AOD,∠CBD
=
∠COD,
●O
D
A
B
C
3.当圆心在圆周角内部时
提示:能否转化为1的情况?
过点B作直径BD.由1可得:
∴
∠ABC
=
∠AOC.
∠ABD
=
∠AOD,∠CBD
=
∠COD,
●O
A
B
C
D
结论:同一条弧所对的圆周角等于它所对圆心角的一半.
结论:
圆周角的定理:
在同圆或等圆中,同弧或等弧所对的圆周角
相等,都等于这条弧所对的圆心角的一半。
由圆周角定理可知:
在同圆或等圆中,如果两个圆周角相等,它们所得对的弧一定相等。
回顾:圆周角定理及推论?
思考:判断正误:
1.同弧或等弧所对的圆周角相等( )
2.相等的圆周角所对的弧相等( )
3.90°角所对的弦是直径( )
4.直径所对的角等于90°(
)
5.长等于半径的弦所对的圆周角等于30°(
)
1、如图,在⊙O中,ABC=50°,
则∠AOC等于(
)
A、50°;
B、80°;
C、90°;
D、100°
A
C
B
O
D
2、如图,△ABC是等边三角形,动点P在圆周的劣弧AB上,且不与A、B重合,则∠BPC等于(
)
A、30°;
B、60°;
C、90°;
D、45°
C
A
B
P
B
练习:
试找出下图中所有相等的圆周角。
A
B
C
D
A
B
C
O
1、如图,已知在⊙
O
中,
∠BOC
=150°,∠A=_____
2、如图,∠A是圆O的圆周角,
∠A=40°,求∠OBC的度数。
B
A
O
.
70°
x
3.求圆中角X的度数
A
O
.
X
120°
C
C
D
B
4、
如图,在直径为AB的半圆中,O为圆心,C、D为半圆上的两点,∠COD=500,则∠CAD=_________
25?
1.半圆或直径所对的圆周角等于多少度?
半圆或直径所对的圆周角是直角
。
90°的圆周角所对的弦是直径
探究二:
O
A
B
C
2.90°的圆周角所对的弦是
否是直径?
例1:如图,AB为⊙O的直径,
∠A=70°,求∠ABC的度数。
A
B
C
O
解:
∵AB为⊙O的直径
∴∠C=90°
∵
∠A=70°
∴
∠B=20
°
例2
:
如图,⊙O直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC、AD、BD的长.
又在Rt△ABD中,AD2+BD2=AB2,
解:∵AB是直径,
∴
∠ACB=
∠ADB=90°.
在Rt△ABC中,
∵CD平分∠ACB,
∴AD=BD.
1.如图AB是⊙O的直径,
C
,D是圆上的两点,若
∠ABD=40°,则∠BCD=_____.
A
B
O
C
D
40°
提示:连接AD
50°
练习
4.如图,
内接于?O,
,
AB=AC,
BD为?O的直径,
AD=6,
则AB=
.BD=_____
C
O
D
B
A
如图:圆内接四边形ABCD中,
∵
∠A的度数等于弧BCD的一
半,∠BCD的度数等于弧BAD的一半,
又∵弧BCD+弧BAD
度数为360°
∴∠A+∠C=
180°.
同理∠B+∠D=180°.
圆内接四边形的对角互补。
探究三
1、如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,
则∠BAD=
∠BCD=
反馈练习:
2、圆内接四边形ABCD中,∠A:∠B:∠C=
2:3:4,则∠A=
∠B=
∠C=
∠D=
50?
130?
60?
90?
120?
90?
3、如图,四边形ABCD内接于⊙O,
∠DCE=75?,
则∠BOD=
150?
A
B
C
D
O
A
B
C
D
E
o
4.已知⊙O中弦AB的等于半径,求弦AB所对
的圆心角和圆周角的度数.
O
A
B
圆心角为60°
圆周角为30°
或150°.
注意:一条弦所对的圆周
角有两种情况,它们的度
数之和为180度。
6.如图,圆心角∠AOB=100°,则∠ACB=___。
O
A
B
C
5、如图,AB是⊙O的直径,
若∠BCD=25°,则∠AOD=
______
130
思维拓展:
1、圆内接平行四边形一定是
形。
2、圆内接梯形一定是
形。
3、圆内接菱形一定是
形。
矩
等腰梯
正方
1._________在圆上,并且角的两边都_________的角叫做圆周角.
2.在同一圆中,一条弧所对的圆周角等于_________圆心角的_________.
3.在同圆或等圆中,____________所对的圆周角____________.
4._________所对的圆周角是直角.90°的圆周角______
是直径.
5.如图,若五边形ABCDE是⊙O的内接正五边形,则∠BOC=______,
∠ABE=______,∠ADC=______,∠ABC=______.
6.如图,若六边形ABCDEF是⊙O的内接正六边形,则∠AED=______,
∠FAE=______,∠DAB=______,∠EFA=______.
7.如图,ΔABC是⊙O的内接正三角形,若P是上一点,
则∠BPC=______;若M是上一点,则∠BMC=______.
8.在⊙O中,若圆心角∠AOB=100°,C是上一点,则∠ACB等于(
).
A.80°
B.100°
C.130°
D.140°
9.在圆中,弦AB,CD相交于E.若∠ADC=46°,∠BCD=33°,则∠DEB等于(
).
A.13°
B.79°
C.38.5°
D.101°
10.如图,AC是⊙O的直径,弦AB∥CD,若∠BAC=32°,
则∠AOD等于(
).
A.64°
B.48°
C.32°
D.76°
11.如图,弦AB,CD相交于E点,若∠BAC=27°,∠BEC=64°,
则∠AOD等于(
).
A.37°
B.74°
C.54°
D.64°
12.如图,四边形ABCD内接于⊙O,若∠BOD=138°,
则它的一个外角∠DCE等于(
).
A.69°
B.42°
C.48°
D.38°
13.如图,△ABC内接于⊙O,∠A=50°,∠ABC=60°,BD是⊙O的直径,
BD交AC于点E,连结DC,则∠AEB等于(
).
A.70°
B.90°
C.110°
D.120°
14.已知:如图,△ABC内接于⊙O,BC=12cm,∠A=60°.求⊙O的直径.
15.已知:如图,AB是⊙O的直径,弦CD⊥AB于E,∠ACD=30°,AE=2cm.求DB长.
16.已知:如图,⊙O的直径AE=10cm,∠B=∠EAC.求AC的长.
同课章节目录
