人教a版 必修二 第一章 1.1 1.1.1 棱柱、棱锥、棱台的结构特征 配套课件
文档属性
| 名称 | 人教a版 必修二 第一章 1.1 1.1.1 棱柱、棱锥、棱台的结构特征 配套课件 |  | |
| 格式 | rar | ||
| 文件大小 | 445.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-08-04 09:03:15 | ||
图片预览








文档简介
(共21张PPT)
第一章
空间几何体
1.1 空间几何体的结构
1.1.1 棱柱、棱锥、棱台的结构特征
1.棱柱至少有___个面,五棱台有___个面.
5
7
4
2.一个棱锥至少有___个面,它既叫___面体,又叫___棱锥.
)
C
3.四棱柱的侧棱及顶点的数目分别为(
A.四条侧棱、四个顶点
B. 八条侧棱、四个顶点
C.四条侧棱、八个顶点
D. 六条侧棱、八个顶点
四
三
)
B
4.过正三棱柱底面一边的截面是(
A.三角形
B.三角形或梯形
C.不是梯形的四边形
D.梯形
1.棱柱的性质:
(1)侧棱都相等,侧面都是平行四边形;
(2)两个底面与平行于底面的截面是全等的多边形;
(3)过不相邻的两条侧棱的截面是平行四边形.
重点 棱柱、正棱锥和正棱台的性质
2.正棱锥的性质:
(1)正棱锥的各侧面都是全等的等腰三角形;
(2)等腰三角形底边上的高(即棱锥的斜高)都相等.
3.正棱台的性质:
(1)各侧棱相等;
(2)正棱台的各侧面都是全等的等腰梯形;
(3)正棱台的斜高相等.
重难点
棱柱的两个本质特征
1.有两个面(底面)相互平行.
2.其余各面(侧面)每相邻两个面的公共边(侧棱)都互相平
行.
因此,棱柱有两个面互相平行,其余各面都是平行四边形.
但是要注意“有两个面互相平行,其余各面都是平行四边形的
几何体”不一定是棱柱.
棱柱、棱锥、棱台的结构特征
例 1:长方体 ABCD-A1B1C1D1 的棱 AB=3,AD=4,AA1
=5,求对角线的长.
长方体 ABCD-A1B1C1D1 的棱 AB=a,AD
=b,AA1=c,对角线 AC1=
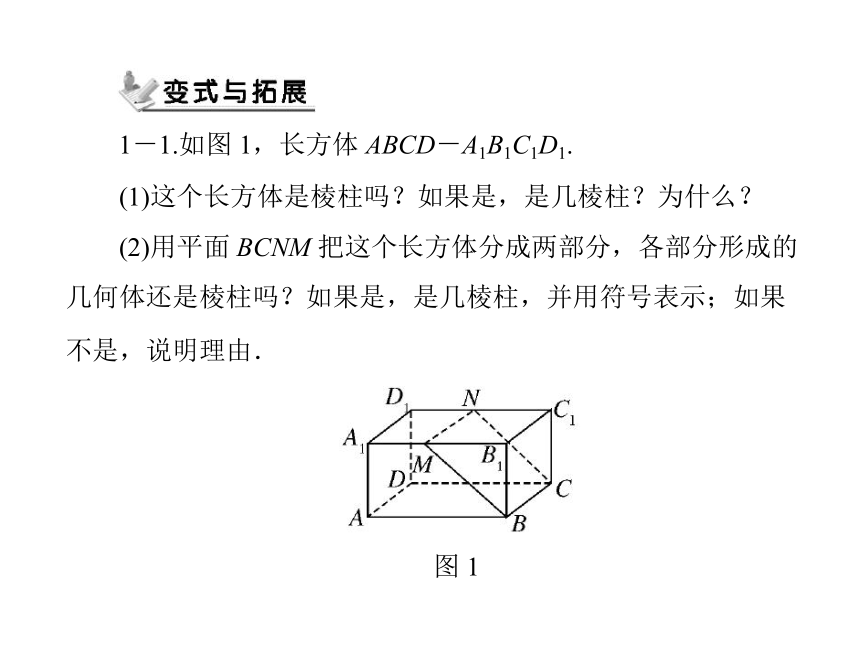
1-1.如图 1,长方体 ABCD-A1B1C1D1.
(1)这个长方体是棱柱吗?如果是,是几棱柱?为什么?
(2)用平面 BCNM 把这个长方体分成两部分,各部分形成的
几何体还是棱柱吗?如果是,是几棱柱,并用符号表示;如果
不是,说明理由.
图 1
解:(1)是棱柱,并且是四棱柱.因为以长方体相对的两个
面作底面都是全等的四边形,其余各面都是矩形,且四条侧棱
互相平行,符合棱柱定义.
(2)截面BCNM 的上方部分是三棱柱BMB1-CNC1,下方部
分是四棱柱 ABMA1-DCND1.
1-2.将 8 个棱长为 1 的正方体按不同的方式摆放成实心长
方体,求所得长方体的对角线的最大值.
解:将 8 个棱长为 1 的正方体排成一排组成长方体,其棱
长分别为 1,1,8,所得长方体的对角线长为
将 8 个棱长为 1 的正方体排成两排组成长方体,其棱长分
别为 1,2,4,所得长方体的对角线长为
将 8 个棱长为 1 的正方体排成正方体,其棱长分别为 2,2,2,
所得长方体的对角线长为
所以长方体的对角线的最大值为
空间想象能力的训练
例 2:下面是一多面体的展开图,如图 2 每个面内都给了字
母,请根据要求回答问题:
图 2
(1) 如 果 A 在 多 面 体 的 底 面 , 那 么 哪 一 面 会 在 上 面
__________;
(2)如果面 F 在前面,从左边看是面 B,那么哪一个面会在
上面__________;
(3)如果从左面看是面 C,面 D 在后面,那么哪一个面会在
上面__________.
答案:(1)F
(2)E
(3)A
2-1.如图 3,纸制的正方体的六个面根据其方位分别标记
为上、下、东、南、西、北.现有沿该正方体的一些棱将正方
体剪开、外面朝上展平,得到右侧的平面图形,则标“△”的面
的方位是(
)
B
图 3
A.南
B.北
C.西
D.下
2-2.如图 4,一个封闭的正方体,它的六个表面各标有 A、
B、C、D、E、F 这六个字母之一,现放置成如图的三种不同的
)
D
位置,则字母 A、B、C 对面的字母分别为(
图 4
A.D、E、F
B.F、D、E
C.E、F、D
D.E、D、F
有关计算问题
例 3:如图 5,正四棱锥 P-ABCD 的底面边长为 a,高为 h,
求它的侧棱 PA 的长和斜高(侧面的高)PE.
图 5
思维突破:把侧棱、斜高分别放到 Rt△PAO、Rt△POE 中,
解三角形即可.
解:∵正四棱锥的底面边长为 a,
空间问题平面化,平面问题三角化.
解:如图 1,设棱台的两底面的中心分别是 O 和 O1,B1C1
和 BC 的中点分别是 E1 和 E,连接 OO1、O1E1、OE、EE1,则
OBB1O1 和 OEE1O1 都是直角梯形.
图 1
3-1.正四棱台 AC1 的高是 17 cm,两底面的边长分别是 4 cm
和 16 cm,求这个棱台的侧棱长和斜高.
∵A1B1=4 cm,AB=16 cm,
∴O1E1=2 cm,OE=8 cm,
例 4:如图 6,长方体 ABCD-A1B1C1D1 中,AB=3,AD=
2,CC1=4,一条绳子从 A 沿着表面拉到 C1,求绳子的最短长
度.
错因剖析:考虑问题不全面以致漏解.
图 6
图 7
则 AC1 的最短长度为
若沿着 AB 剪开如图 8,
图 8
正解:将长方体沿着 AA1 剪开,如图 7,
4-1.长方体三条棱长分别是 AA′=1,AB=2,AD=4,则
从 A 点出发,沿长方体的表面到 C′的最短矩离是(
)
A.5
B.7
A
第一章
空间几何体
1.1 空间几何体的结构
1.1.1 棱柱、棱锥、棱台的结构特征
1.棱柱至少有___个面,五棱台有___个面.
5
7
4
2.一个棱锥至少有___个面,它既叫___面体,又叫___棱锥.
)
C
3.四棱柱的侧棱及顶点的数目分别为(
A.四条侧棱、四个顶点
B. 八条侧棱、四个顶点
C.四条侧棱、八个顶点
D. 六条侧棱、八个顶点
四
三
)
B
4.过正三棱柱底面一边的截面是(
A.三角形
B.三角形或梯形
C.不是梯形的四边形
D.梯形
1.棱柱的性质:
(1)侧棱都相等,侧面都是平行四边形;
(2)两个底面与平行于底面的截面是全等的多边形;
(3)过不相邻的两条侧棱的截面是平行四边形.
重点 棱柱、正棱锥和正棱台的性质
2.正棱锥的性质:
(1)正棱锥的各侧面都是全等的等腰三角形;
(2)等腰三角形底边上的高(即棱锥的斜高)都相等.
3.正棱台的性质:
(1)各侧棱相等;
(2)正棱台的各侧面都是全等的等腰梯形;
(3)正棱台的斜高相等.
重难点
棱柱的两个本质特征
1.有两个面(底面)相互平行.
2.其余各面(侧面)每相邻两个面的公共边(侧棱)都互相平
行.
因此,棱柱有两个面互相平行,其余各面都是平行四边形.
但是要注意“有两个面互相平行,其余各面都是平行四边形的
几何体”不一定是棱柱.
棱柱、棱锥、棱台的结构特征
例 1:长方体 ABCD-A1B1C1D1 的棱 AB=3,AD=4,AA1
=5,求对角线的长.
长方体 ABCD-A1B1C1D1 的棱 AB=a,AD
=b,AA1=c,对角线 AC1=
1-1.如图 1,长方体 ABCD-A1B1C1D1.
(1)这个长方体是棱柱吗?如果是,是几棱柱?为什么?
(2)用平面 BCNM 把这个长方体分成两部分,各部分形成的
几何体还是棱柱吗?如果是,是几棱柱,并用符号表示;如果
不是,说明理由.
图 1
解:(1)是棱柱,并且是四棱柱.因为以长方体相对的两个
面作底面都是全等的四边形,其余各面都是矩形,且四条侧棱
互相平行,符合棱柱定义.
(2)截面BCNM 的上方部分是三棱柱BMB1-CNC1,下方部
分是四棱柱 ABMA1-DCND1.
1-2.将 8 个棱长为 1 的正方体按不同的方式摆放成实心长
方体,求所得长方体的对角线的最大值.
解:将 8 个棱长为 1 的正方体排成一排组成长方体,其棱
长分别为 1,1,8,所得长方体的对角线长为
将 8 个棱长为 1 的正方体排成两排组成长方体,其棱长分
别为 1,2,4,所得长方体的对角线长为
将 8 个棱长为 1 的正方体排成正方体,其棱长分别为 2,2,2,
所得长方体的对角线长为
所以长方体的对角线的最大值为
空间想象能力的训练
例 2:下面是一多面体的展开图,如图 2 每个面内都给了字
母,请根据要求回答问题:
图 2
(1) 如 果 A 在 多 面 体 的 底 面 , 那 么 哪 一 面 会 在 上 面
__________;
(2)如果面 F 在前面,从左边看是面 B,那么哪一个面会在
上面__________;
(3)如果从左面看是面 C,面 D 在后面,那么哪一个面会在
上面__________.
答案:(1)F
(2)E
(3)A
2-1.如图 3,纸制的正方体的六个面根据其方位分别标记
为上、下、东、南、西、北.现有沿该正方体的一些棱将正方
体剪开、外面朝上展平,得到右侧的平面图形,则标“△”的面
的方位是(
)
B
图 3
A.南
B.北
C.西
D.下
2-2.如图 4,一个封闭的正方体,它的六个表面各标有 A、
B、C、D、E、F 这六个字母之一,现放置成如图的三种不同的
)
D
位置,则字母 A、B、C 对面的字母分别为(
图 4
A.D、E、F
B.F、D、E
C.E、F、D
D.E、D、F
有关计算问题
例 3:如图 5,正四棱锥 P-ABCD 的底面边长为 a,高为 h,
求它的侧棱 PA 的长和斜高(侧面的高)PE.
图 5
思维突破:把侧棱、斜高分别放到 Rt△PAO、Rt△POE 中,
解三角形即可.
解:∵正四棱锥的底面边长为 a,
空间问题平面化,平面问题三角化.
解:如图 1,设棱台的两底面的中心分别是 O 和 O1,B1C1
和 BC 的中点分别是 E1 和 E,连接 OO1、O1E1、OE、EE1,则
OBB1O1 和 OEE1O1 都是直角梯形.
图 1
3-1.正四棱台 AC1 的高是 17 cm,两底面的边长分别是 4 cm
和 16 cm,求这个棱台的侧棱长和斜高.
∵A1B1=4 cm,AB=16 cm,
∴O1E1=2 cm,OE=8 cm,
例 4:如图 6,长方体 ABCD-A1B1C1D1 中,AB=3,AD=
2,CC1=4,一条绳子从 A 沿着表面拉到 C1,求绳子的最短长
度.
错因剖析:考虑问题不全面以致漏解.
图 6
图 7
则 AC1 的最短长度为
若沿着 AB 剪开如图 8,
图 8
正解:将长方体沿着 AA1 剪开,如图 7,
4-1.长方体三条棱长分别是 AA′=1,AB=2,AD=4,则
从 A 点出发,沿长方体的表面到 C′的最短矩离是(
)
A.5
B.7
A
