人教a版 必修二 第二章 2.1 2.1.1 平面 配套课件
文档属性
| 名称 | 人教a版 必修二 第二章 2.1 2.1.1 平面 配套课件 |  | |
| 格式 | rar | ||
| 文件大小 | 401.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-08-04 09:03:15 | ||
图片预览





文档简介
(共19张PPT)
第二章
点、直线、平面之间的位置关系
2.1 空间点、直线、平面之间的位置关系
2.1.1 平面
1.下列命题正确的是(
)
C
A.画一个平面,使它的长为 14 cm,宽为 5 cm
B.一个平面的面积可以是 16 m2
C.平面内的一条直线把这个平面分成两部分,一个平面把
空间分成两部分
D.10 个平面重叠起来,要比 2 个平面重叠起来厚
2.下列命题正确的是(
)
C
A.因为直线向两方无限延伸,所以直线不可能在平面内
B.如果线段的中点在平面内,那么线段在平面内
C.如果线段上有一个点不在平面内,那么线段不在平面内
D.当平面经过直线时,直线上可以有不在平面内的点
3.下列说法中正确的是(
)
C
A.两个平面相交有两条交线
B.两个平面可以有且只有一个公共点
C.如果一个点在两个平面内,那么这个点在两个平面的交
线上
D.两个平面一定有公共点
)
B
重点
公理及其推论
1.平面基本性质即三条公理的“文字语言”、“符号语
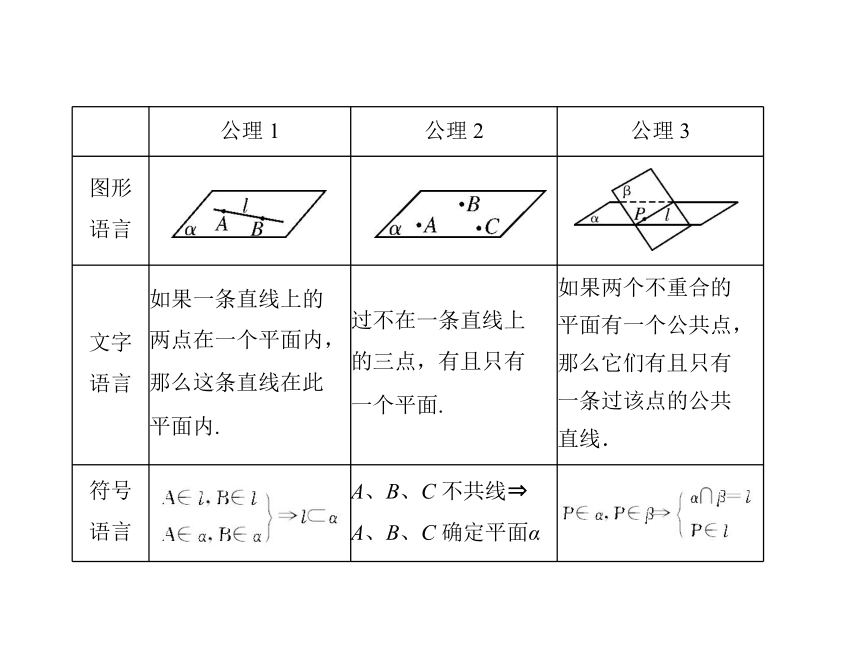
言”、“图形语言”列表如下:
公理 1 公理 2 公理 3
图形
语言
文字
语言 如果一条直线上的
两点在一个平面内,
那么这条直线在此
平面内. 过不在一条直线上
的三点,有且只有
一个平面. 如果两个不重合的
平面有一个公共点,
那么它们有且只有
一条过该点的公共
直线.
符号
语言 A、B、C 不共线
A、B、C 确定平面α
2.公理 2 的三条推论:
推论 1 经过一条直线和这条直线外的一点,有且只有一个
平面;
推论 2 经过两条相交直线,有且只有一个平面;
推论 3 经过两条平行直线,有且只有一个平面.
难点
公理及其推论的应用
1.公理 1 既可以判断直线是否在平面内,点是否在平面内,
又可以利用直线检验平面.
2.公理 2 的作用:
(1)确定平面;
(2)证明点、线共面.
3.公理 3 的作用:
(1)判断两个平面是否相交;
(2)确定两个平面的交线;
(3)证明若干点共线问题.
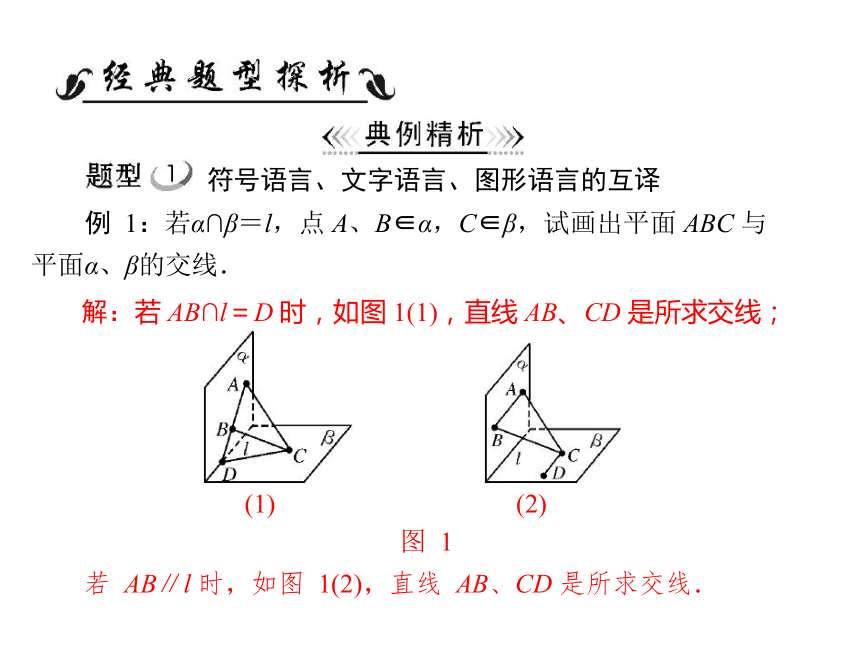
符号语言、文字语言、图形语言的互译
例 1:若α∩β=l,点 A、B∈α,C∈β,试画出平面 ABC 与
平面α、β的交线.
(1)
(2)
图 1
若 AB∥l 时,如图 1(2),直线 AB、CD 是所求交线.
解:若 AB∩l=D 时,如图 1(1),直线 AB、CD 是所求交线;
正确地用图形和符号表示点、直线、平面以
及它们之间的关系.点看成是元素,线、面看成是点的集合,
所以点与线、面的关系用“∈、 ”表示,线与线、线与面及面
与面的关系用“ 、 ”表示.
1-1.试用集合符号表示下列各语句,并画出图形:
(1)点 A 在平面α内,但不在平面β内;
(2)直线 l 经过平面α外一点 P,且与平面α相交于点 M;
(3)平面α与平面β相交于直线 l,且 l 经过点 P.
解:(1)A∈α,A β,此处图形不唯一,符合要求即可,如
图 11(1).
图 11
(2)P∈l,P α,l∩α=M,如图 11(2).
(3)α∩β=l,P∈l,如图 11(3).
点线共面问题
例 2:求证:两两相交且不过同一个点的三条直线必在同一
平面内.
解:已知:直线 AB、BC、CA 两两相交,交点分别为 A、B、
C(如图 2).求证:直线 AB、BC、CA 共面.
图 2
证明:∵AB∩CA=A,
思维突破:根据题目写出已知、求证后,再进行证明.
证明线共面一般先用公理 2 及其推论证两
条直线确定一个平面,再用公理 1 证明余下的直线也在它们确
定的平面内.
∴直线 AB 和 AC 确定一个平面α(推论 2).
因此,直线 AB、BC、CA 都在平面α内,即它们共面.
图 3
证明:∵PQ∥a,
∴PQ 与 a 确定一个平面β,
∴直线 a β,点 P∈β.
∵P∈b,b α,∴P∈α.
又∵a α,
∴α与β重合,∴PQ α.
2-1.如图 3,已知:a α,b α,a∩b=A,P∈b,PQ∥a,
求证:PQ α.
多点共线问题
例 3:已知:EF∩GH=P,E∈AB,F∈AD,G∈BC,H∈
CD,求证:B、D、P 三点共线.
思维突破:应用公理 3,选择恰当的平面,只要证明此三点
都是某两个平面的公共点,即可证三点在这两个平面的交线上.
∵AB∩BD=B,
∴AB 和 BD 确定平面 ABD.
∵A∈AB,D∈BD,
∴AD 平面 ABD(公理 1).
∵E∈AB,F∈AD,∴EF 平面 ABD.
又∵EF∩GH=P,∴P∈平面 ABD.
同理,P∈平面 BCD.
∵BD 平面 ABD,BD 平面 BCD,
∴平面 ABD∩平面 BCD=BD.
∴P∈BD,即 B、D、P 三点共线.
证明:如图 4.
图 4
证明若干点共线问题的基本方法:
①首先找出两个平面的交线,然后证明这若干点都是这两
个平面的公共点,根据公理 3 可推知这些点都在交线上,即证
若干点共线;
②选择其中两点确定一条直线,然后证明另一些点都在这
条直线上.
3-1.△ABC 在平面α外,AB∩α=P,BC∩α=Q,AC∩α
=R,求证:P、Q、R 三点共线.
∴P、Q、R∈α
①,P∈AB,Q∈BC,R∈AC ②,
由②可得 P、Q、R∈ABC,
∴P、Q、R 是平面 ABC 与平面α的公共点,
∵两平面相交有且只有一条交线,
∴P、Q、R 三点在平面 ABC 与平面α的交线上,
即 P、Q、R 三点共线.
证明:AB∩α=P,BC∩α=Q,AC∩α=R,
例 4:如图 5,在正方体 ABCD-A′B′C′D′中,E、F
分别是 AA′、AB 上一点,且 EF∥CD′,求证:平面 EFCD′、
平面 AC 与平面 AD′两两相交的交线 ED′、FC、AD 交于一点.
图 5
错因剖析:遇到此类证明多线共点问题,找不到解决问题
的突破口.
证明:∵E、F 分别是 AA′与 AB 上一点,∴EF≠CD′.
又∵EF∥CD′,
∴四边形 EFCD′是梯形,直线 ED′和 FC 相交于一点,
设此点为 P,
∵P∈ED′ 平面 AA′D′D,P∈FC 平面 ABCD,
∴P 是平面 AA′D′D 与平面 ABCD 的公共点.
∵平面 AA′D′D∩平面 ABCD=AD,∴P∈AD.
∴ED′、FC、AD 交于一点 P.
先证两条直线交于一点,再证第三条直线
经过这点,把问题化归到证明点在直线上的问题.
4-1.三个平面两两相交得到三条交线,如果其中有两条相
交于一点,那么第三条也经过这个点.
解:已知:平面α 、β、γ满足α∩β=a,β∩γ=b,γ∩α=c,
a∩b=A,如图12.求证:A∈c.
图 12
证明:∵a∩b=A,∴A∈a,A∈b.
又∵α∩β=a,β∩γ=b,∴a α,b γ.
∴A∈α,A∈γ.
即 A 在平面α与平面γ的交线上,
又α∩γ=c,∴A∈c.
第二章
点、直线、平面之间的位置关系
2.1 空间点、直线、平面之间的位置关系
2.1.1 平面
1.下列命题正确的是(
)
C
A.画一个平面,使它的长为 14 cm,宽为 5 cm
B.一个平面的面积可以是 16 m2
C.平面内的一条直线把这个平面分成两部分,一个平面把
空间分成两部分
D.10 个平面重叠起来,要比 2 个平面重叠起来厚
2.下列命题正确的是(
)
C
A.因为直线向两方无限延伸,所以直线不可能在平面内
B.如果线段的中点在平面内,那么线段在平面内
C.如果线段上有一个点不在平面内,那么线段不在平面内
D.当平面经过直线时,直线上可以有不在平面内的点
3.下列说法中正确的是(
)
C
A.两个平面相交有两条交线
B.两个平面可以有且只有一个公共点
C.如果一个点在两个平面内,那么这个点在两个平面的交
线上
D.两个平面一定有公共点
)
B
重点
公理及其推论
1.平面基本性质即三条公理的“文字语言”、“符号语
言”、“图形语言”列表如下:
公理 1 公理 2 公理 3
图形
语言
文字
语言 如果一条直线上的
两点在一个平面内,
那么这条直线在此
平面内. 过不在一条直线上
的三点,有且只有
一个平面. 如果两个不重合的
平面有一个公共点,
那么它们有且只有
一条过该点的公共
直线.
符号
语言 A、B、C 不共线
A、B、C 确定平面α
2.公理 2 的三条推论:
推论 1 经过一条直线和这条直线外的一点,有且只有一个
平面;
推论 2 经过两条相交直线,有且只有一个平面;
推论 3 经过两条平行直线,有且只有一个平面.
难点
公理及其推论的应用
1.公理 1 既可以判断直线是否在平面内,点是否在平面内,
又可以利用直线检验平面.
2.公理 2 的作用:
(1)确定平面;
(2)证明点、线共面.
3.公理 3 的作用:
(1)判断两个平面是否相交;
(2)确定两个平面的交线;
(3)证明若干点共线问题.
符号语言、文字语言、图形语言的互译
例 1:若α∩β=l,点 A、B∈α,C∈β,试画出平面 ABC 与
平面α、β的交线.
(1)
(2)
图 1
若 AB∥l 时,如图 1(2),直线 AB、CD 是所求交线.
解:若 AB∩l=D 时,如图 1(1),直线 AB、CD 是所求交线;
正确地用图形和符号表示点、直线、平面以
及它们之间的关系.点看成是元素,线、面看成是点的集合,
所以点与线、面的关系用“∈、 ”表示,线与线、线与面及面
与面的关系用“ 、 ”表示.
1-1.试用集合符号表示下列各语句,并画出图形:
(1)点 A 在平面α内,但不在平面β内;
(2)直线 l 经过平面α外一点 P,且与平面α相交于点 M;
(3)平面α与平面β相交于直线 l,且 l 经过点 P.
解:(1)A∈α,A β,此处图形不唯一,符合要求即可,如
图 11(1).
图 11
(2)P∈l,P α,l∩α=M,如图 11(2).
(3)α∩β=l,P∈l,如图 11(3).
点线共面问题
例 2:求证:两两相交且不过同一个点的三条直线必在同一
平面内.
解:已知:直线 AB、BC、CA 两两相交,交点分别为 A、B、
C(如图 2).求证:直线 AB、BC、CA 共面.
图 2
证明:∵AB∩CA=A,
思维突破:根据题目写出已知、求证后,再进行证明.
证明线共面一般先用公理 2 及其推论证两
条直线确定一个平面,再用公理 1 证明余下的直线也在它们确
定的平面内.
∴直线 AB 和 AC 确定一个平面α(推论 2).
因此,直线 AB、BC、CA 都在平面α内,即它们共面.
图 3
证明:∵PQ∥a,
∴PQ 与 a 确定一个平面β,
∴直线 a β,点 P∈β.
∵P∈b,b α,∴P∈α.
又∵a α,
∴α与β重合,∴PQ α.
2-1.如图 3,已知:a α,b α,a∩b=A,P∈b,PQ∥a,
求证:PQ α.
多点共线问题
例 3:已知:EF∩GH=P,E∈AB,F∈AD,G∈BC,H∈
CD,求证:B、D、P 三点共线.
思维突破:应用公理 3,选择恰当的平面,只要证明此三点
都是某两个平面的公共点,即可证三点在这两个平面的交线上.
∵AB∩BD=B,
∴AB 和 BD 确定平面 ABD.
∵A∈AB,D∈BD,
∴AD 平面 ABD(公理 1).
∵E∈AB,F∈AD,∴EF 平面 ABD.
又∵EF∩GH=P,∴P∈平面 ABD.
同理,P∈平面 BCD.
∵BD 平面 ABD,BD 平面 BCD,
∴平面 ABD∩平面 BCD=BD.
∴P∈BD,即 B、D、P 三点共线.
证明:如图 4.
图 4
证明若干点共线问题的基本方法:
①首先找出两个平面的交线,然后证明这若干点都是这两
个平面的公共点,根据公理 3 可推知这些点都在交线上,即证
若干点共线;
②选择其中两点确定一条直线,然后证明另一些点都在这
条直线上.
3-1.△ABC 在平面α外,AB∩α=P,BC∩α=Q,AC∩α
=R,求证:P、Q、R 三点共线.
∴P、Q、R∈α
①,P∈AB,Q∈BC,R∈AC ②,
由②可得 P、Q、R∈ABC,
∴P、Q、R 是平面 ABC 与平面α的公共点,
∵两平面相交有且只有一条交线,
∴P、Q、R 三点在平面 ABC 与平面α的交线上,
即 P、Q、R 三点共线.
证明:AB∩α=P,BC∩α=Q,AC∩α=R,
例 4:如图 5,在正方体 ABCD-A′B′C′D′中,E、F
分别是 AA′、AB 上一点,且 EF∥CD′,求证:平面 EFCD′、
平面 AC 与平面 AD′两两相交的交线 ED′、FC、AD 交于一点.
图 5
错因剖析:遇到此类证明多线共点问题,找不到解决问题
的突破口.
证明:∵E、F 分别是 AA′与 AB 上一点,∴EF≠CD′.
又∵EF∥CD′,
∴四边形 EFCD′是梯形,直线 ED′和 FC 相交于一点,
设此点为 P,
∵P∈ED′ 平面 AA′D′D,P∈FC 平面 ABCD,
∴P 是平面 AA′D′D 与平面 ABCD 的公共点.
∵平面 AA′D′D∩平面 ABCD=AD,∴P∈AD.
∴ED′、FC、AD 交于一点 P.
先证两条直线交于一点,再证第三条直线
经过这点,把问题化归到证明点在直线上的问题.
4-1.三个平面两两相交得到三条交线,如果其中有两条相
交于一点,那么第三条也经过这个点.
解:已知:平面α 、β、γ满足α∩β=a,β∩γ=b,γ∩α=c,
a∩b=A,如图12.求证:A∈c.
图 12
证明:∵a∩b=A,∴A∈a,A∈b.
又∵α∩β=a,β∩γ=b,∴a α,b γ.
∴A∈α,A∈γ.
即 A 在平面α与平面γ的交线上,
又α∩γ=c,∴A∈c.
