人教a版 必修二 第三章 3.3 3.3.1 两条直线的交点坐标 配套课件
文档属性
| 名称 | 人教a版 必修二 第三章 3.3 3.3.1 两条直线的交点坐标 配套课件 |  | |
| 格式 | rar | ||
| 文件大小 | 316.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-08-04 09:03:15 | ||
图片预览






文档简介
(共17张PPT)
3.3 直线的交点坐标与距离公式
3.3.1 两条直线的交点坐标
1.直线 3x+5y-1=0 与直线 4x+3y-5=0 的交点是(
)
C
A.(-2,1)
C.(2,-1)
B.(-3,2)
D.(2,-2)
2.两条直线 2x+3y-k=0 与直线 x-ky+12=0 的交点在
)
y 轴上,那么 k 的值是(
A.-24
C.±6
B.6
D.以上都不对
C
3.如果直线 ax+2y+2=0 与直线 3x-y-2=0 平行,那么
)
B
系数 a 为(
A.-3
B.-6
C.-
3
2
D.
2
3
4.过点(-1,3)且垂直于直线 x-2y+3=0 的直线方程为
(
)
A
A.2x+y-1=0
C.x+2y-5=0
B.2x+y-5=0
D.x-2y+7=0
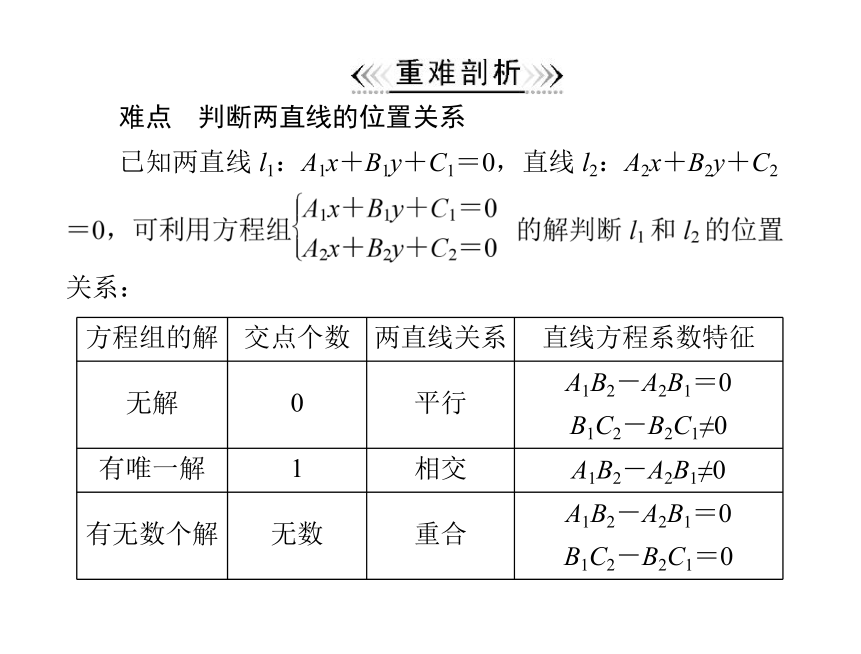
方程组的解 交点个数 两直线关系 直线方程系数特征
无解 0 平行 A1B2-A2B1=0
B1C2-B2C1≠0
有唯一解 1 相交 A1B2-A2B1≠0
有无数个解 无数 重合 A1B2-A2B1=0
B1C2-B2C1=0
难点
判断两直线的位置关系
已知两直线 l1:A1x+B1y+C1=0,直线 l2:A2x+B2y+C2
关系:
判断两直线的位置关系
例 1: 分别判断下列直线是否相交,若相交,求出它们的交
点.
(1)l1:2x-y=7 和 l2:3x+2y-7=0;
(2)l1:2x-6y+4=0 和 l2:4x-12y+8=0;
(3)l1:4x+2y+4=0 和 l2:y=-2x+3.
思维突破:可依据方程组解的情况来判断两直线的位置关
系.
因此直线 l1 和 l2 相交,交点坐标为(3,-1).
这表明直线 l1 和 l2 重合.
这表明直线 l1 和 l2 没有公共点,故 l1∥l2.
1-1.求直线 l1:3x+4y-5=0 与直线 l2:2x-3y+8=0 的
交点 M 的坐标.
解:由 l1 与 l2 的方程联立方程组
∴点 M 的坐标为(-1,2).
证明:应用过两直线交点的直线系方程,将方程整理为 a(3x
-y)+(-x+2y-1)=0.
直线恒过定点问题
例 2:已知直线(a-2)y=(3a-1)x-1.求证:无论 a 为何值
直线总经过一定点.
(1)曲线过定点,即与参数无关,则参数的同
次幂的系数为0,从而可求出定点.(2)分别令参数为两个特殊值,
得方程组,求出点的坐标代入原方程,若满足,则此点为定点.
2-1.已知直线方程为(2+λ)x+(1-2λ)y+4-3λ=0.
求证:不论λ取何实数值,此直线必过定点.
即点(-1,-2)适合方程 2x+y+4+λ(x-2y-3)=0,也就
是适合方程(2+λ)x+(1-2λ)y+4-3λ=0.所以,不论λ取何实数
值,直线(2+λ)x+(1-2λ)y+4-3λ=0 必过定点(-1,-2).
证明:把直线方程整理为 2x+y+4+λ(x-2y-3)=0.解方
讨论两直线的位置关系
例 3:已知两直线 l1:mx+y-(m+1)=0 和 l2:x+my-2m
=0,问实数 m 取何值时,l1 与 l2 分别是下列位置关系:
(1)相交;(2)平行;(3)重合;
(4)垂直;(5)交点在第一象限.
思维突破:可由方程中的未知数的系数取值决定直线的位
置关系.
①×m-②得(m2-1)x=m2-m
③.
代入方程组得 y=
2m+1
m+1
,方程组有唯一的解.
因此,当且仅当 m≠±1 时,l1 与 l2 相交.
(2)由(1)中的方程③知,m=-1 时得 0=2 方程无解,即方
程组无解,两直线平行.
因此,当且仅当 m=-1 时,l1 与 l2 平行.
(3)由(1)中的方程③知,m=1 时得 0=0,方程有无数多解,
即方程组有无数多解,两直线重合.
因此,当且仅当 m=1 时,l1 与 l2 重合.
(4)因为 m≠±1 时,l1 与 l2 相交;
当 m=0 时,l1 的斜率为 0,l2 的斜率不存在,l1⊥l2;
因此,当且仅当 m=0 时,l1⊥l2.
(1)用方程组思想解决两直线平行、垂直问
题时,应分有斜率和没有斜率两种情况来解决,不要漏解.(2)
讨论交点位置时要注意方程组有唯一解的条件,如(5)中,易漏
掉m≠±1这一条件.本题也可把方程向斜截式转化再进行讨论.
因此,m<-1 或 m>0 且 m≠1 时,交点在第一象限.
3-1.已知直线 l1:x+my+6=0,l2:(m-2)x+3y+2m=0,
求 m 的值,使得:
(1)l1 和 l2 相交;(2)l1⊥l2;(3)l1∥l2;(4)l1 和 l2 重合.
解:(1)l1 和 l2 相交 1×3-(m-2)m≠0,
∴m2-2m-3≠0 m≠-1,或 m≠3,
∴当 m≠-1 且 m≠3 时,l1 和 l2 相交.
(3)∵m=0 时,l1 不平行 l2,
(4)∵m=0 时,l1 与 l2 不重合,
正解:由题意可得两直线平行,当 a=0 时,直线 x+6=0
和-2x=0 平行,没有公共点;
当 a=-1 时,直线 x+y+6=0 和-3x-3y-2=0 平行,
没有公共点,
当 a=3 时,直线 x+9y+6=0 和 x+9y+6=0 重合,有无
数个公共点,不满足题意,应舍去.
综上,a 的值为 0 或-1.
例 4:若直线 x+a2y+6=0 和直线(a-2)x+3ay+2a=0 没
有公共点,则 a 的值是__________.
错因剖析:忽略 a=0 的情形.
4-1.若三条直线 l1:x-y=0;l2:x+y-2=0;l3:5x-ky
-15=0 围成一个三角形,则 k 的取值范围是(
)
B
A.k∈R 且 k≠±5 且 k≠1
B.k∈R 且 k≠±5 且 k≠-10
C.k∈R 且 k≠±1 且 k≠0
D.k∈R 且 k≠±5
解析:三条直线如果有两条平行或三条直线交于一点时就
不能围成三角形.
3.3 直线的交点坐标与距离公式
3.3.1 两条直线的交点坐标
1.直线 3x+5y-1=0 与直线 4x+3y-5=0 的交点是(
)
C
A.(-2,1)
C.(2,-1)
B.(-3,2)
D.(2,-2)
2.两条直线 2x+3y-k=0 与直线 x-ky+12=0 的交点在
)
y 轴上,那么 k 的值是(
A.-24
C.±6
B.6
D.以上都不对
C
3.如果直线 ax+2y+2=0 与直线 3x-y-2=0 平行,那么
)
B
系数 a 为(
A.-3
B.-6
C.-
3
2
D.
2
3
4.过点(-1,3)且垂直于直线 x-2y+3=0 的直线方程为
(
)
A
A.2x+y-1=0
C.x+2y-5=0
B.2x+y-5=0
D.x-2y+7=0
方程组的解 交点个数 两直线关系 直线方程系数特征
无解 0 平行 A1B2-A2B1=0
B1C2-B2C1≠0
有唯一解 1 相交 A1B2-A2B1≠0
有无数个解 无数 重合 A1B2-A2B1=0
B1C2-B2C1=0
难点
判断两直线的位置关系
已知两直线 l1:A1x+B1y+C1=0,直线 l2:A2x+B2y+C2
关系:
判断两直线的位置关系
例 1: 分别判断下列直线是否相交,若相交,求出它们的交
点.
(1)l1:2x-y=7 和 l2:3x+2y-7=0;
(2)l1:2x-6y+4=0 和 l2:4x-12y+8=0;
(3)l1:4x+2y+4=0 和 l2:y=-2x+3.
思维突破:可依据方程组解的情况来判断两直线的位置关
系.
因此直线 l1 和 l2 相交,交点坐标为(3,-1).
这表明直线 l1 和 l2 重合.
这表明直线 l1 和 l2 没有公共点,故 l1∥l2.
1-1.求直线 l1:3x+4y-5=0 与直线 l2:2x-3y+8=0 的
交点 M 的坐标.
解:由 l1 与 l2 的方程联立方程组
∴点 M 的坐标为(-1,2).
证明:应用过两直线交点的直线系方程,将方程整理为 a(3x
-y)+(-x+2y-1)=0.
直线恒过定点问题
例 2:已知直线(a-2)y=(3a-1)x-1.求证:无论 a 为何值
直线总经过一定点.
(1)曲线过定点,即与参数无关,则参数的同
次幂的系数为0,从而可求出定点.(2)分别令参数为两个特殊值,
得方程组,求出点的坐标代入原方程,若满足,则此点为定点.
2-1.已知直线方程为(2+λ)x+(1-2λ)y+4-3λ=0.
求证:不论λ取何实数值,此直线必过定点.
即点(-1,-2)适合方程 2x+y+4+λ(x-2y-3)=0,也就
是适合方程(2+λ)x+(1-2λ)y+4-3λ=0.所以,不论λ取何实数
值,直线(2+λ)x+(1-2λ)y+4-3λ=0 必过定点(-1,-2).
证明:把直线方程整理为 2x+y+4+λ(x-2y-3)=0.解方
讨论两直线的位置关系
例 3:已知两直线 l1:mx+y-(m+1)=0 和 l2:x+my-2m
=0,问实数 m 取何值时,l1 与 l2 分别是下列位置关系:
(1)相交;(2)平行;(3)重合;
(4)垂直;(5)交点在第一象限.
思维突破:可由方程中的未知数的系数取值决定直线的位
置关系.
①×m-②得(m2-1)x=m2-m
③.
代入方程组得 y=
2m+1
m+1
,方程组有唯一的解.
因此,当且仅当 m≠±1 时,l1 与 l2 相交.
(2)由(1)中的方程③知,m=-1 时得 0=2 方程无解,即方
程组无解,两直线平行.
因此,当且仅当 m=-1 时,l1 与 l2 平行.
(3)由(1)中的方程③知,m=1 时得 0=0,方程有无数多解,
即方程组有无数多解,两直线重合.
因此,当且仅当 m=1 时,l1 与 l2 重合.
(4)因为 m≠±1 时,l1 与 l2 相交;
当 m=0 时,l1 的斜率为 0,l2 的斜率不存在,l1⊥l2;
因此,当且仅当 m=0 时,l1⊥l2.
(1)用方程组思想解决两直线平行、垂直问
题时,应分有斜率和没有斜率两种情况来解决,不要漏解.(2)
讨论交点位置时要注意方程组有唯一解的条件,如(5)中,易漏
掉m≠±1这一条件.本题也可把方程向斜截式转化再进行讨论.
因此,m<-1 或 m>0 且 m≠1 时,交点在第一象限.
3-1.已知直线 l1:x+my+6=0,l2:(m-2)x+3y+2m=0,
求 m 的值,使得:
(1)l1 和 l2 相交;(2)l1⊥l2;(3)l1∥l2;(4)l1 和 l2 重合.
解:(1)l1 和 l2 相交 1×3-(m-2)m≠0,
∴m2-2m-3≠0 m≠-1,或 m≠3,
∴当 m≠-1 且 m≠3 时,l1 和 l2 相交.
(3)∵m=0 时,l1 不平行 l2,
(4)∵m=0 时,l1 与 l2 不重合,
正解:由题意可得两直线平行,当 a=0 时,直线 x+6=0
和-2x=0 平行,没有公共点;
当 a=-1 时,直线 x+y+6=0 和-3x-3y-2=0 平行,
没有公共点,
当 a=3 时,直线 x+9y+6=0 和 x+9y+6=0 重合,有无
数个公共点,不满足题意,应舍去.
综上,a 的值为 0 或-1.
例 4:若直线 x+a2y+6=0 和直线(a-2)x+3ay+2a=0 没
有公共点,则 a 的值是__________.
错因剖析:忽略 a=0 的情形.
4-1.若三条直线 l1:x-y=0;l2:x+y-2=0;l3:5x-ky
-15=0 围成一个三角形,则 k 的取值范围是(
)
B
A.k∈R 且 k≠±5 且 k≠1
B.k∈R 且 k≠±5 且 k≠-10
C.k∈R 且 k≠±1 且 k≠0
D.k∈R 且 k≠±5
解析:三条直线如果有两条平行或三条直线交于一点时就
不能围成三角形.
