25.3.1 用频率估计概率课件(26张PPT)
文档属性
| 名称 | 25.3.1 用频率估计概率课件(26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-24 13:40:27 | ||
图片预览






文档简介
第 二十五章 概率初步
25.3 用频率估计概率
第1课时
2020年秋人教版数学九年级上册精品课件
学 习 目 标
知道通过大量重复试验,可以用频率估计概率(重点).
了解用频率估计概率的合理性和必要性,培养随机观念.
1
2
新 课 导 入
知识回顾
一般地,如果在一次试验中,有n种可能的结果,并且它们 ,事件A包含其中的 种结果,那么事件A发生的概率P(A)= .则:P(A)的 取值范围是 .
发生的可能性相等
m
0≤ ≤1
问题引入
抛掷一枚质地均匀的硬币,“正面向上”的概率为0.5.
这是否意味着:
“抛掷 2 次,1 次正面向上”?
“抛掷 50 次,25 次正面向上”?
.
新课导入
我们不妨用试验进行检验.
探究频率与概率的关系
问题1 抛掷一枚硬币,正面(有数字的一面)向上的概率是二分之一,这个概率能否利用试验的方法──通过统计很多掷硬币的结果来得到呢?
新 课 讲 解
掷硬币试验
新课讲解
【试验要求】
1.全班同学分组,每组六名同学分为三小组,分别做投掷试验。
2.统计试验结果,按要求计算频率(频率结果保留两位小数),
向组长汇报,并由组长填写好表格.投掷试验的总次数不少于100次.
3.组长将表格交给老师.
探究1:
试验投掷时要细心、认真哟!
新课讲解
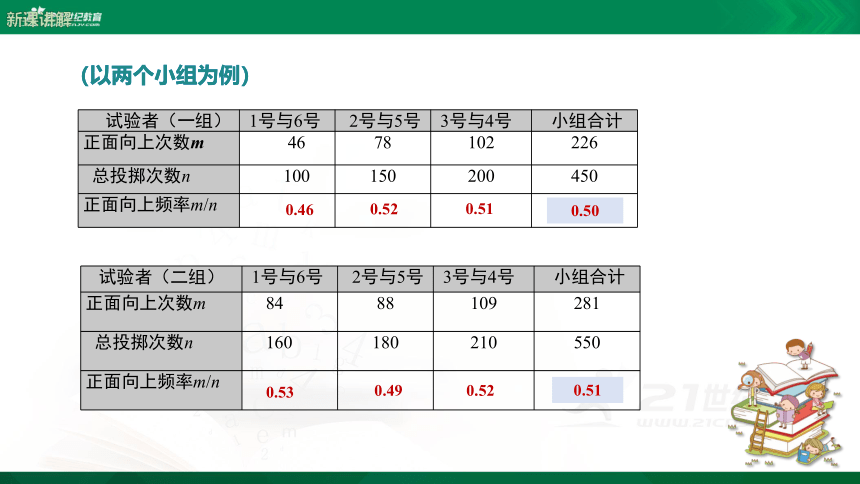
(以两个小组为例)
试验者(一组)
1号与6号
2号与5号
3号与4号
小组合计
正面向上次数m
46
78
102
226
总投掷次数n
100
150
200
450
正面向上频率m/n
试验者(二组)
1号与6号
2号与5号
3号与4号
小组合计
正面向上次数m
84
88
109
281
总投掷次数n
160
180
210
550
正面向上频率m/n
(以两个小组为例)
0.46
0.52
0.51
0.502
0.53
0.49
0.52
0.510
0.50
0.51
新课讲解
试验者
一组
二组
三组
四组
五组
六组
全班
合计
正面向
上次数m
226
281
260
238
246
259
总投掷
次数n
450
550
503
487
510
495
正面向上频率m/n
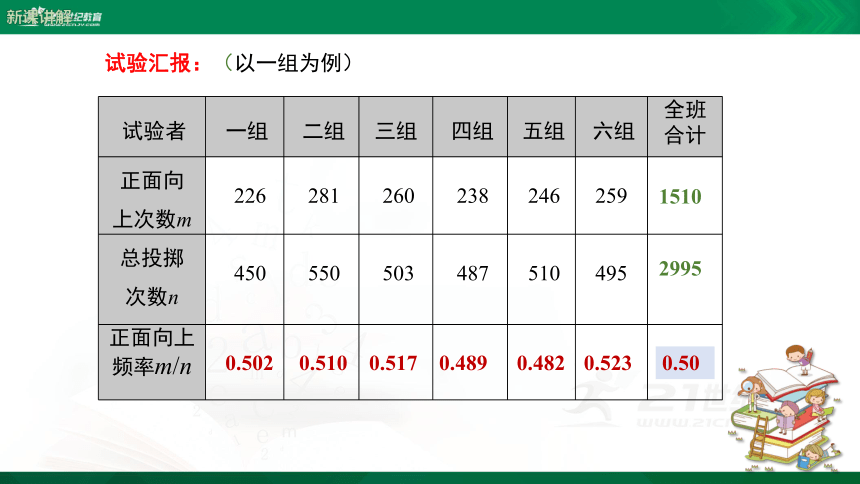
试验汇报:(以一组为例)
0.502
0.510
0.517
0.489
0.482
1510
2995
0.523
0.504
0.50
新课讲解
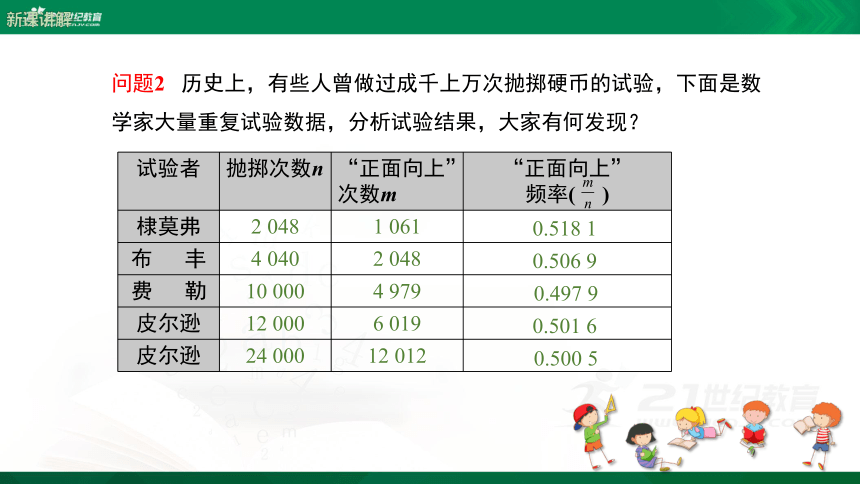
问题2 历史上,有些人曾做过成千上万次抛掷硬币的试验,下面是数学家大量重复试验数据,分析试验结果,大家有何发现?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}试验者
抛掷次数n
“正面向上”次数m
“正面向上”
频率( )
棣莫弗
2 048
1 061
布 丰
4 040
2 048
费 勒
10 000
4 979
皮尔逊
12 000
6 019
皮尔逊
24 000
12 012
0.518 1
0.506 9
0.497 9
0.501 6
0.500 5
新课讲解
问题3 把上面表格中数学家大量重复试验数据,绘制在直角坐标系中,观察各点,
大家有何发现?
试验次数越多频率越接近0. 5,即频率稳定于概率.
抛掷次数n
0.5
2048
4040
10000
12000
24000
“正面向上”
频率( )
0
新课讲解
问题4 为什么可以用频率估计概率?
一般地,在大量重复试验中,如果事件A发生的概率 会
稳定在某个常数p附近,那么事件A发生的概率P(A)=p.
概率是针对大量重复试验而言,并非在每一次试验中都发生
新课讲解
问题5 频率与概率有什么区别与联系?
所谓频率,是在相同条件下进行重复试验时事件发生的次数与试验总次数的比值,其本身是随机的,在试验前不能够确定,且随着试验的不同而发生改变. 而一个随机事件发生的概率是确定的常数,是客观存在的,与试验次数无关. 从以上角度上讲,频率与概率是有区别的,但在大量的重复试验中,随机事件发生的频率会呈现出明显的规律性:随着试验次数的增加,频率将会越来越集中在一个常数附近,具有稳定性,即试验频率稳定于其理论概率.
新课讲解
对一般的随机事件,在做大量重复试验时,随着试验次数的增加,一个事件出现的频率,总是在一个固定数的附近摆动,显示出一定的稳定性.
总结:
因此,我们可以通过大量的重复试验,用一个随机事件发生的频率去估计它的概率.
频率稳定性
雅各布·伯努利
(1654-1705)
新课讲解
频率稳定性说明随机事件发生的可能性大小是随机事件本身固有的规律,频率的稳定性不仅被实践不断证明,而且瑞士数学家雅各布·伯努利以定理的形式给予了严格的证明.因而他被公认为是概率论的先驱之一.
数学史料
新课讲解
活动:抛掷一枚图钉 50 次,统计“钉尖朝上”出现的频数,用 Excel 逐步累加全班数据,观察频率变化 折线图,估计“钉尖朝上”的概率.
注意:水平拿图钉,如图,从视线高度松手,让图钉下落,尽可能保证每次试验条件相同,确保试验的随机性.
抛掷一枚图钉,估计“钉尖朝上”的概率.
探究2:
新课讲解
某篮球队教练记录该队一名主力前锋练习罚篮的结果如下:
(1)填表(精确到0.001);
(2)比赛中该前锋队员上篮得分并造成对手犯规,罚篮一次,你能估计这次他能罚中的概率是多少吗?
练习罚篮次数
30
60
90
150
200
300
400
500
罚中次数
27
45
78
118
161
239
322
401
罚中频率
0.900
0.750
0.867
0.787
0.805
0.797
0.805
0.802
解:从表中的数据可以发现,随着练习次数的增加,该前锋罚篮命中的频率稳定在0.8左右,所以估计他这次能罚中的概率约为0.8.
例题
在一个不透明的盒子里装有除颜色不同其余均相同的黑、白两种球,其中白球24个,黑球若干.小兵将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是试验中的一组统计数据:
摸球的次数n
100
200
300
500
800
1000
3000
摸到白球次数m
65
124
178
302
481
599
1803
摸到白球概率
0.65
0.62
0.593
0.604
0.601
0.599
0.601
(1)请估计:当n很大时,摸到白球的频率将会接近 (精确到0.1);
(2)假如你摸一次,估计你摸到白球的概率P(白球)= .
0.6
0.6
新课讲解
练一练
????????
?
1.在一个不透明的布袋中,红色、黑色、白色的玻璃球共有60个,除颜色外,形状、大小、质地等完全相同.小刚通过多次摸球试验后发现其中摸到红色、黑色球的频率稳定在0.15和0.45,则口袋中白色球的个数很可能是( )
A.12 B.24
C.36 D.48
随 堂 训 练
B
2.下表记录了一名球员在罚球线上投篮的结果:
(1)计算投中频率(结果保留小数点后两位);
随堂训练
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}投蓝次数n
50
100
150
200
250
300
500
投中次数m
28
60
78
104
123
152
251
投中频率
0.60
0.56
0.52
0.52
0.50
0.50
0.49
(2)这名球员投篮一次,投中的概率约是多少(结果保留小数点后一位)?
解:(1)由题意得,这名球员投篮的次数为1400次,投中的次数为720,故这名球员投篮一次,投中的频率约为7961550=0.51.
?
分析:计算出所有投篮的次数,在计算出总的命中数,可以求出投中频率,继而可估计出这名球员投篮一次,投中的概率.
随堂训练
(2)这名球员投篮一次,投中的概率约是0.5.
频率估计概率
大量重复试验
求非等可能性事件概率
列举法
不能适应
频率稳定
常数附近
统计思想
用样本(频率)估计总体(概率)
一种关系
频率与概率的关系
频率稳定时可看作是概率
但概率与频率无关
随 堂 小 结
随堂小结
所谓频率,是在相同条件下进行重复试验时事件发生的次数与试验总次数的比值,其本身是随机的,在试验前不能够确定,且随着试验的不同而发生改变. 而一个随机事件发生的概率是确定的常数,是客观存在的,与试验次数无关. 从以上角度上讲,频率与概率是有区别的,但在大量的重复试验中,随机事件发生的频率会呈现出明显的规律性:随着试验次数的增加,频率将会越来越集中在一个常数附近,具有稳定性,即试验频率稳定于其理论概率.
教科书第144页 练习题 第1,2 题, 第147页 习题25.3 第3题.
布 置 作 业
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
25.3 用频率估计概率
第1课时
2020年秋人教版数学九年级上册精品课件
学 习 目 标
知道通过大量重复试验,可以用频率估计概率(重点).
了解用频率估计概率的合理性和必要性,培养随机观念.
1
2
新 课 导 入
知识回顾
一般地,如果在一次试验中,有n种可能的结果,并且它们 ,事件A包含其中的 种结果,那么事件A发生的概率P(A)= .则:P(A)的 取值范围是 .
发生的可能性相等
m
0≤ ≤1
问题引入
抛掷一枚质地均匀的硬币,“正面向上”的概率为0.5.
这是否意味着:
“抛掷 2 次,1 次正面向上”?
“抛掷 50 次,25 次正面向上”?
.
新课导入
我们不妨用试验进行检验.
探究频率与概率的关系
问题1 抛掷一枚硬币,正面(有数字的一面)向上的概率是二分之一,这个概率能否利用试验的方法──通过统计很多掷硬币的结果来得到呢?
新 课 讲 解
掷硬币试验
新课讲解
【试验要求】
1.全班同学分组,每组六名同学分为三小组,分别做投掷试验。
2.统计试验结果,按要求计算频率(频率结果保留两位小数),
向组长汇报,并由组长填写好表格.投掷试验的总次数不少于100次.
3.组长将表格交给老师.
探究1:
试验投掷时要细心、认真哟!
新课讲解
(以两个小组为例)
试验者(一组)
1号与6号
2号与5号
3号与4号
小组合计
正面向上次数m
46
78
102
226
总投掷次数n
100
150
200
450
正面向上频率m/n
试验者(二组)
1号与6号
2号与5号
3号与4号
小组合计
正面向上次数m
84
88
109
281
总投掷次数n
160
180
210
550
正面向上频率m/n
(以两个小组为例)
0.46
0.52
0.51
0.502
0.53
0.49
0.52
0.510
0.50
0.51
新课讲解
试验者
一组
二组
三组
四组
五组
六组
全班
合计
正面向
上次数m
226
281
260
238
246
259
总投掷
次数n
450
550
503
487
510
495
正面向上频率m/n
试验汇报:(以一组为例)
0.502
0.510
0.517
0.489
0.482
1510
2995
0.523
0.504
0.50
新课讲解
问题2 历史上,有些人曾做过成千上万次抛掷硬币的试验,下面是数学家大量重复试验数据,分析试验结果,大家有何发现?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}试验者
抛掷次数n
“正面向上”次数m
“正面向上”
频率( )
棣莫弗
2 048
1 061
布 丰
4 040
2 048
费 勒
10 000
4 979
皮尔逊
12 000
6 019
皮尔逊
24 000
12 012
0.518 1
0.506 9
0.497 9
0.501 6
0.500 5
新课讲解
问题3 把上面表格中数学家大量重复试验数据,绘制在直角坐标系中,观察各点,
大家有何发现?
试验次数越多频率越接近0. 5,即频率稳定于概率.
抛掷次数n
0.5
2048
4040
10000
12000
24000
“正面向上”
频率( )
0
新课讲解
问题4 为什么可以用频率估计概率?
一般地,在大量重复试验中,如果事件A发生的概率 会
稳定在某个常数p附近,那么事件A发生的概率P(A)=p.
概率是针对大量重复试验而言,并非在每一次试验中都发生
新课讲解
问题5 频率与概率有什么区别与联系?
所谓频率,是在相同条件下进行重复试验时事件发生的次数与试验总次数的比值,其本身是随机的,在试验前不能够确定,且随着试验的不同而发生改变. 而一个随机事件发生的概率是确定的常数,是客观存在的,与试验次数无关. 从以上角度上讲,频率与概率是有区别的,但在大量的重复试验中,随机事件发生的频率会呈现出明显的规律性:随着试验次数的增加,频率将会越来越集中在一个常数附近,具有稳定性,即试验频率稳定于其理论概率.
新课讲解
对一般的随机事件,在做大量重复试验时,随着试验次数的增加,一个事件出现的频率,总是在一个固定数的附近摆动,显示出一定的稳定性.
总结:
因此,我们可以通过大量的重复试验,用一个随机事件发生的频率去估计它的概率.
频率稳定性
雅各布·伯努利
(1654-1705)
新课讲解
频率稳定性说明随机事件发生的可能性大小是随机事件本身固有的规律,频率的稳定性不仅被实践不断证明,而且瑞士数学家雅各布·伯努利以定理的形式给予了严格的证明.因而他被公认为是概率论的先驱之一.
数学史料
新课讲解
活动:抛掷一枚图钉 50 次,统计“钉尖朝上”出现的频数,用 Excel 逐步累加全班数据,观察频率变化 折线图,估计“钉尖朝上”的概率.
注意:水平拿图钉,如图,从视线高度松手,让图钉下落,尽可能保证每次试验条件相同,确保试验的随机性.
抛掷一枚图钉,估计“钉尖朝上”的概率.
探究2:
新课讲解
某篮球队教练记录该队一名主力前锋练习罚篮的结果如下:
(1)填表(精确到0.001);
(2)比赛中该前锋队员上篮得分并造成对手犯规,罚篮一次,你能估计这次他能罚中的概率是多少吗?
练习罚篮次数
30
60
90
150
200
300
400
500
罚中次数
27
45
78
118
161
239
322
401
罚中频率
0.900
0.750
0.867
0.787
0.805
0.797
0.805
0.802
解:从表中的数据可以发现,随着练习次数的增加,该前锋罚篮命中的频率稳定在0.8左右,所以估计他这次能罚中的概率约为0.8.
例题
在一个不透明的盒子里装有除颜色不同其余均相同的黑、白两种球,其中白球24个,黑球若干.小兵将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是试验中的一组统计数据:
摸球的次数n
100
200
300
500
800
1000
3000
摸到白球次数m
65
124
178
302
481
599
1803
摸到白球概率
0.65
0.62
0.593
0.604
0.601
0.599
0.601
(1)请估计:当n很大时,摸到白球的频率将会接近 (精确到0.1);
(2)假如你摸一次,估计你摸到白球的概率P(白球)= .
0.6
0.6
新课讲解
练一练
????????
?
1.在一个不透明的布袋中,红色、黑色、白色的玻璃球共有60个,除颜色外,形状、大小、质地等完全相同.小刚通过多次摸球试验后发现其中摸到红色、黑色球的频率稳定在0.15和0.45,则口袋中白色球的个数很可能是( )
A.12 B.24
C.36 D.48
随 堂 训 练
B
2.下表记录了一名球员在罚球线上投篮的结果:
(1)计算投中频率(结果保留小数点后两位);
随堂训练
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}投蓝次数n
50
100
150
200
250
300
500
投中次数m
28
60
78
104
123
152
251
投中频率
0.60
0.56
0.52
0.52
0.50
0.50
0.49
(2)这名球员投篮一次,投中的概率约是多少(结果保留小数点后一位)?
解:(1)由题意得,这名球员投篮的次数为1400次,投中的次数为720,故这名球员投篮一次,投中的频率约为7961550=0.51.
?
分析:计算出所有投篮的次数,在计算出总的命中数,可以求出投中频率,继而可估计出这名球员投篮一次,投中的概率.
随堂训练
(2)这名球员投篮一次,投中的概率约是0.5.
频率估计概率
大量重复试验
求非等可能性事件概率
列举法
不能适应
频率稳定
常数附近
统计思想
用样本(频率)估计总体(概率)
一种关系
频率与概率的关系
频率稳定时可看作是概率
但概率与频率无关
随 堂 小 结
随堂小结
所谓频率,是在相同条件下进行重复试验时事件发生的次数与试验总次数的比值,其本身是随机的,在试验前不能够确定,且随着试验的不同而发生改变. 而一个随机事件发生的概率是确定的常数,是客观存在的,与试验次数无关. 从以上角度上讲,频率与概率是有区别的,但在大量的重复试验中,随机事件发生的频率会呈现出明显的规律性:随着试验次数的增加,频率将会越来越集中在一个常数附近,具有稳定性,即试验频率稳定于其理论概率.
教科书第144页 练习题 第1,2 题, 第147页 习题25.3 第3题.
布 置 作 业
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
