25.3.2 用频率估计概率课件(22张PPT)
文档属性
| 名称 | 25.3.2 用频率估计概率课件(22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-24 13:41:53 | ||
图片预览







文档简介
第 二十五章 概率初步
25.3 用频率估计概率
第2课时
2020年秋人教版数学九年级上册精品课件
学 习 目 标
用频率估计概率并解决实际问题(重点).
新 课 导 入
知识回顾
对一般的随机事件,在做大量的重复试验时,随着试验次数的增加,一个事件出现的频率,总在一个固定数的附近摆动,显示出一定的稳定性.
因此,在以通过大量的重复试验,用一个随机事件发生的频率估计它的概率.
问题引入
问题 在生活中你还遇到过哪些用频率估计概率的
实际问题?
.
新课导入
问题1 某林业部门要考察某种幼树在一定条件的移植成活率,就采用什么具体做法?
新 课 讲 解
探究新知
分析:幼树移植成活率是实际问题中的一种 ,成活率要由 去估计.
频率
概率
概率的综合应用
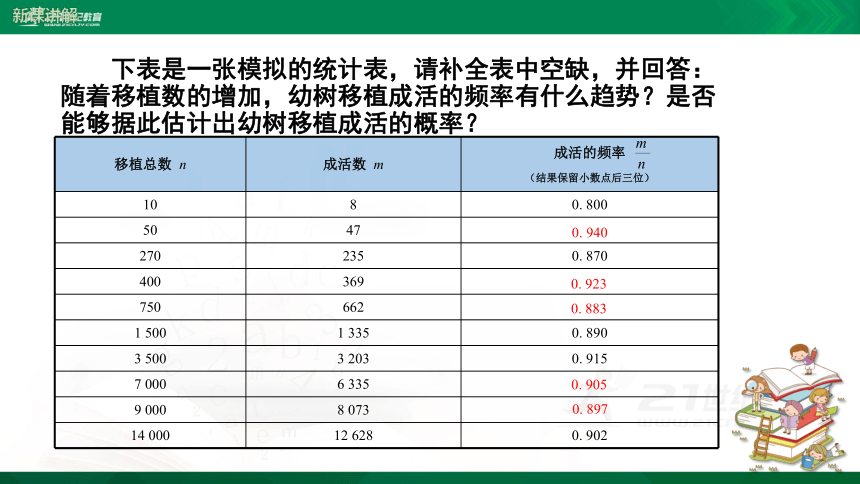
下表是一张模拟的统计表,请补全表中空缺,并回答:随着移植数的增加,幼树移植成活的频率有什么趋势?是否能够据此估计出幼树移植成活的概率?
移植总数 n
成活数 m
成活的频率
(结果保留小数点后三位)
10
8
0. 800
50
47
270
235
0. 870
400
369
750
662
1 500
1 335
0. 890
3 500
3 203
0. 915
7 000
6 335
9 000
8 073
14 000
12 628
0. 902
0. 940
0. 923
0. 883
0. 905
0. 897
新课讲解
新课讲解
从上表可以发现,随着移植数的增加,幼树移植成活的频率越来越稳定,当移植总数 为14 000时,成活的频率为0.902,于是可以估计幼树移植成活的概率为0.9.
解:
在同样的条件下,对这种幼树进行大量移植随着移植数n会越来越大,频率 会越来越 .于是就可以把频率作为 的估计值.
成活率
稳定
某水果公司以 2 元/ kg 的成本价新进 10 000 kg
柑橘.如果公司希望这些柑橘能够获得利润 5 000 元,
那么在出售柑橘(去掉损坏的柑橘)时,每千克大约定
价为多少元比较合适?
新课讲解
问题2
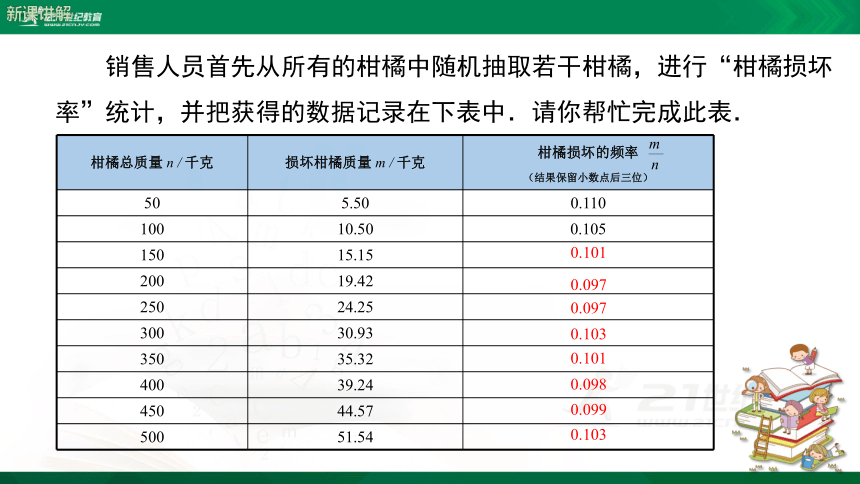
销售人员首先从所有的柑橘中随机抽取若干柑橘,进行“柑橘损坏率”统计,并把获得的数据记录在下表中.请你帮忙完成此表.
柑橘总质量 n / 千克
损坏柑橘质量 m / 千克
柑橘损坏的频率
(结果保留小数点后三位)
50
5.50
0.110
100
10.50
0.105
150
15.15
200
19.42
250
24.25
300
30.93
350
35.32
400
39.24
450
44.57
500
51.54
新课讲解
0.101
0.097
0.097
0.103
0.101
0.098
0.099
0.103
若柑橘没有损坏,要获得 5 000 元利润应如何定价?
柑橘损坏后,柑橘的重量减少了,为了确保获得5 000 元利润,定价应如何变化?
如何知道柑橘的重量将减少多少?
新课讲解
思考
分析:用什么办法估计柑橘的损坏率?
随着统计的频率越来越稳定,柑橘的损坏率为 0.1,
则柑橘的完好概率为 0.9.
设每千克柑橘的售价为x 元,
根据“利润=(售价-实际成本) × 完好的质量”列方程求解.
?
新课讲解
销售人员已经对柑橘损坏率进行了抽样统计,填完表格后可以看出,随着柑橘质量的增加,柑橘损坏的频率越来越稳定.柑橘总质量为 500 kg 时的损坏频率为 0.103,于是可以估计柑橘损坏的概率约为 0.1(结果保留小数点后一位).由此可知,柑橘完好的概率为0.9.
新课讲解
解:
根据估计的概率可以知道,在 10 000 kg 柑橘中完
好柑橘的质量为
10 000×0.9=9 000(kg).
设每千克柑橘售价为 x 元,则
(??????2×10?0009?000)×9?000=5?000.
解得 x ≈ 2.8(元).
答:出售柑橘时,每千克大约定价 2.8 元可获利
润 5 000元.
?
新课讲解
1. 某农科所在相同条件下做某作物种子发芽率的试验,结果如下表所示:
一般地,1 000 kg 种子中大约有多少是不能发芽的?
种子个数
发芽种子个数
发芽种子频
(结果保留小数点后三位)
100
94
200
187
300
282
400
338
500
435
600
530
700
624
800
718
900
814
1 000
901
随堂训练
种子个数
发芽种子个数
发芽种子频率
100
94
200
187
300
282
400
338
500
435
600
530
700
624
800
718
900
814
1000
901
0.940
0.935
0.940
0.898
0.845
0.870
0.883
0.891
0.904
0.901
发芽概率估计为0.9,1000kg种子中大约有100kg不能发芽.
随堂训练
解:填表如下
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A} 试验种子n(粒)
1
5
50
100
200
500
1000
2000
3000
发芽频数m
1
4
45
92
188
476
951
1900
2850
发芽频率
1
0.80
0.90
0.92
0.94
0.952
0.951
a
b
(1)计算表中a、b的值;
(2)估计该麦种的发芽概率;
(3)如果该麦种发芽后,只有87%的麦芽可以成活,现有100 kg麦种,则有多少千克的麦种可以成活为秧苗?
2.在同样条件下对某种小麦种子进行发芽试验,统计发芽种子数,获得如下频数表.
随堂训练
随堂训练
解:(1)a=1900÷2000=0.95,b=2850÷3000=0.95.
(2)观察发现,随着大量重复试验,发芽频率逐渐稳定到常数0.95附近,所以该麦种的发芽概率约为0.95.
(3)100×0.95×87%=82.65(千克),故有82.65千克的麦种可以成活为秧苗.
总结:
在大量重复试验中,如果某个事件发生的频率呈现稳定性,此时可以用频率的稳定值估计事件发生的概率.
随 堂 小 结
(1)你能列举一些生活中用频率估计概率的例子吗?
(2)通过本节课的学习你有哪些收获?
教科书第148页 习题25.3第5,6题.
布 置 作 业
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
25.3 用频率估计概率
第2课时
2020年秋人教版数学九年级上册精品课件
学 习 目 标
用频率估计概率并解决实际问题(重点).
新 课 导 入
知识回顾
对一般的随机事件,在做大量的重复试验时,随着试验次数的增加,一个事件出现的频率,总在一个固定数的附近摆动,显示出一定的稳定性.
因此,在以通过大量的重复试验,用一个随机事件发生的频率估计它的概率.
问题引入
问题 在生活中你还遇到过哪些用频率估计概率的
实际问题?
.
新课导入
问题1 某林业部门要考察某种幼树在一定条件的移植成活率,就采用什么具体做法?
新 课 讲 解
探究新知
分析:幼树移植成活率是实际问题中的一种 ,成活率要由 去估计.
频率
概率
概率的综合应用
下表是一张模拟的统计表,请补全表中空缺,并回答:随着移植数的增加,幼树移植成活的频率有什么趋势?是否能够据此估计出幼树移植成活的概率?
移植总数 n
成活数 m
成活的频率
(结果保留小数点后三位)
10
8
0. 800
50
47
270
235
0. 870
400
369
750
662
1 500
1 335
0. 890
3 500
3 203
0. 915
7 000
6 335
9 000
8 073
14 000
12 628
0. 902
0. 940
0. 923
0. 883
0. 905
0. 897
新课讲解
新课讲解
从上表可以发现,随着移植数的增加,幼树移植成活的频率越来越稳定,当移植总数 为14 000时,成活的频率为0.902,于是可以估计幼树移植成活的概率为0.9.
解:
在同样的条件下,对这种幼树进行大量移植随着移植数n会越来越大,频率 会越来越 .于是就可以把频率作为 的估计值.
成活率
稳定
某水果公司以 2 元/ kg 的成本价新进 10 000 kg
柑橘.如果公司希望这些柑橘能够获得利润 5 000 元,
那么在出售柑橘(去掉损坏的柑橘)时,每千克大约定
价为多少元比较合适?
新课讲解
问题2
销售人员首先从所有的柑橘中随机抽取若干柑橘,进行“柑橘损坏率”统计,并把获得的数据记录在下表中.请你帮忙完成此表.
柑橘总质量 n / 千克
损坏柑橘质量 m / 千克
柑橘损坏的频率
(结果保留小数点后三位)
50
5.50
0.110
100
10.50
0.105
150
15.15
200
19.42
250
24.25
300
30.93
350
35.32
400
39.24
450
44.57
500
51.54
新课讲解
0.101
0.097
0.097
0.103
0.101
0.098
0.099
0.103
若柑橘没有损坏,要获得 5 000 元利润应如何定价?
柑橘损坏后,柑橘的重量减少了,为了确保获得5 000 元利润,定价应如何变化?
如何知道柑橘的重量将减少多少?
新课讲解
思考
分析:用什么办法估计柑橘的损坏率?
随着统计的频率越来越稳定,柑橘的损坏率为 0.1,
则柑橘的完好概率为 0.9.
设每千克柑橘的售价为x 元,
根据“利润=(售价-实际成本) × 完好的质量”列方程求解.
?
新课讲解
销售人员已经对柑橘损坏率进行了抽样统计,填完表格后可以看出,随着柑橘质量的增加,柑橘损坏的频率越来越稳定.柑橘总质量为 500 kg 时的损坏频率为 0.103,于是可以估计柑橘损坏的概率约为 0.1(结果保留小数点后一位).由此可知,柑橘完好的概率为0.9.
新课讲解
解:
根据估计的概率可以知道,在 10 000 kg 柑橘中完
好柑橘的质量为
10 000×0.9=9 000(kg).
设每千克柑橘售价为 x 元,则
(??????2×10?0009?000)×9?000=5?000.
解得 x ≈ 2.8(元).
答:出售柑橘时,每千克大约定价 2.8 元可获利
润 5 000元.
?
新课讲解
1. 某农科所在相同条件下做某作物种子发芽率的试验,结果如下表所示:
一般地,1 000 kg 种子中大约有多少是不能发芽的?
种子个数
发芽种子个数
发芽种子频
(结果保留小数点后三位)
100
94
200
187
300
282
400
338
500
435
600
530
700
624
800
718
900
814
1 000
901
随堂训练
种子个数
发芽种子个数
发芽种子频率
100
94
200
187
300
282
400
338
500
435
600
530
700
624
800
718
900
814
1000
901
0.940
0.935
0.940
0.898
0.845
0.870
0.883
0.891
0.904
0.901
发芽概率估计为0.9,1000kg种子中大约有100kg不能发芽.
随堂训练
解:填表如下
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A} 试验种子n(粒)
1
5
50
100
200
500
1000
2000
3000
发芽频数m
1
4
45
92
188
476
951
1900
2850
发芽频率
1
0.80
0.90
0.92
0.94
0.952
0.951
a
b
(1)计算表中a、b的值;
(2)估计该麦种的发芽概率;
(3)如果该麦种发芽后,只有87%的麦芽可以成活,现有100 kg麦种,则有多少千克的麦种可以成活为秧苗?
2.在同样条件下对某种小麦种子进行发芽试验,统计发芽种子数,获得如下频数表.
随堂训练
随堂训练
解:(1)a=1900÷2000=0.95,b=2850÷3000=0.95.
(2)观察发现,随着大量重复试验,发芽频率逐渐稳定到常数0.95附近,所以该麦种的发芽概率约为0.95.
(3)100×0.95×87%=82.65(千克),故有82.65千克的麦种可以成活为秧苗.
总结:
在大量重复试验中,如果某个事件发生的频率呈现稳定性,此时可以用频率的稳定值估计事件发生的概率.
随 堂 小 结
(1)你能列举一些生活中用频率估计概率的例子吗?
(2)通过本节课的学习你有哪些收获?
教科书第148页 习题25.3第5,6题.
布 置 作 业
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
