北师大版数学八年级上册 1. 1 探索勾股定理练习课件(共23张PPT)
文档属性
| 名称 | 北师大版数学八年级上册 1. 1 探索勾股定理练习课件(共23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 701.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-23 16:02:45 | ||
图片预览



文档简介
第一章 勾股定理
1 探索勾股定理
名师导学
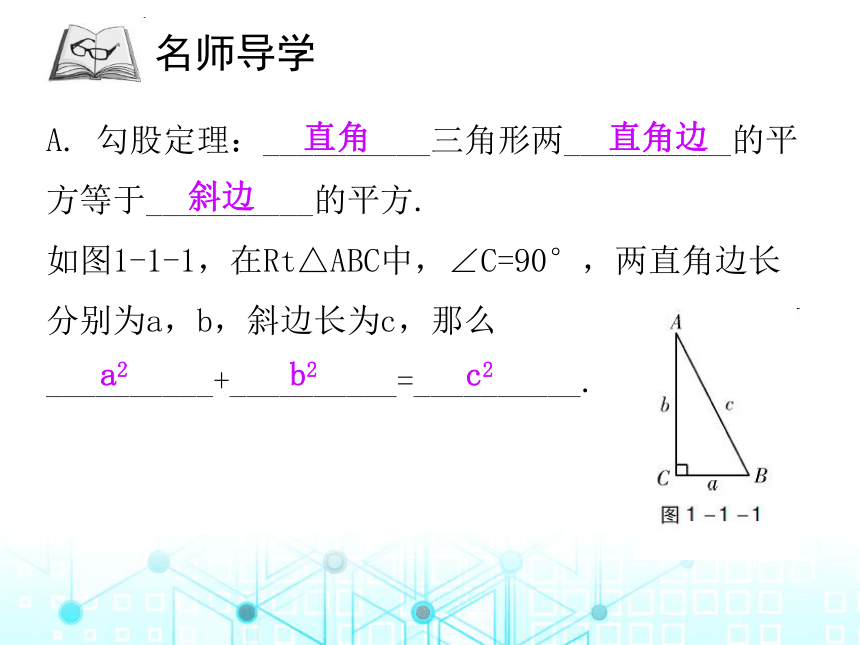
A. 勾股定理:__________三角形两__________的平方等于__________的平方.
如图1-1-1,在Rt△ABC中,∠C=90°,两直角边长分别为a,b,斜边长为c,那么__________+__________=__________.
直角
直角边
斜边
a2
b2
c2
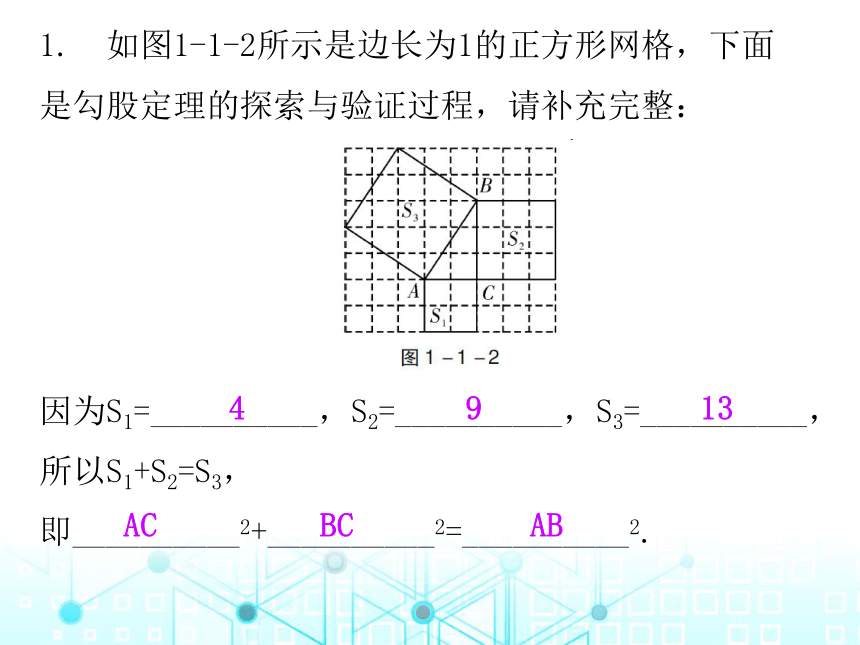
1. 如图1-1-2所示是边长为1的正方形网格,下面是勾股定理的探索与验证过程,请补充完整:
因为S1=__________,S2=__________,S3=__________,
所以S1+S2=S3,
即__________2+__________2=__________2.
4
9
13
AC
BC
AB
课堂讲练
新知1:勾股定理的定义
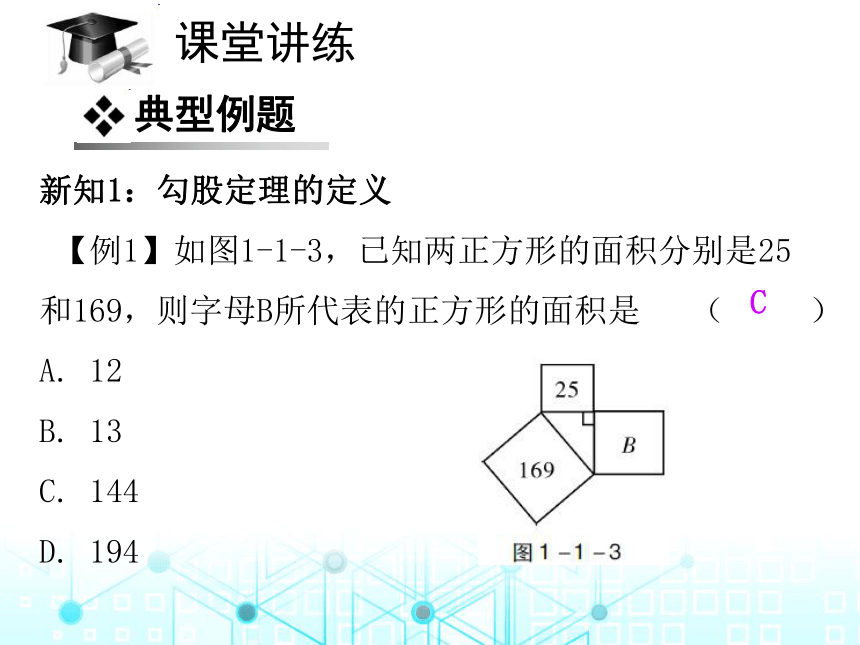
【例1】如图1-1-3,已知两正方形的面积分别是25和169,则字母B所代表的正方形的面积是 ( )
A. 12
B. 13
C. 144
D. 194
C
典型例题
模拟演练
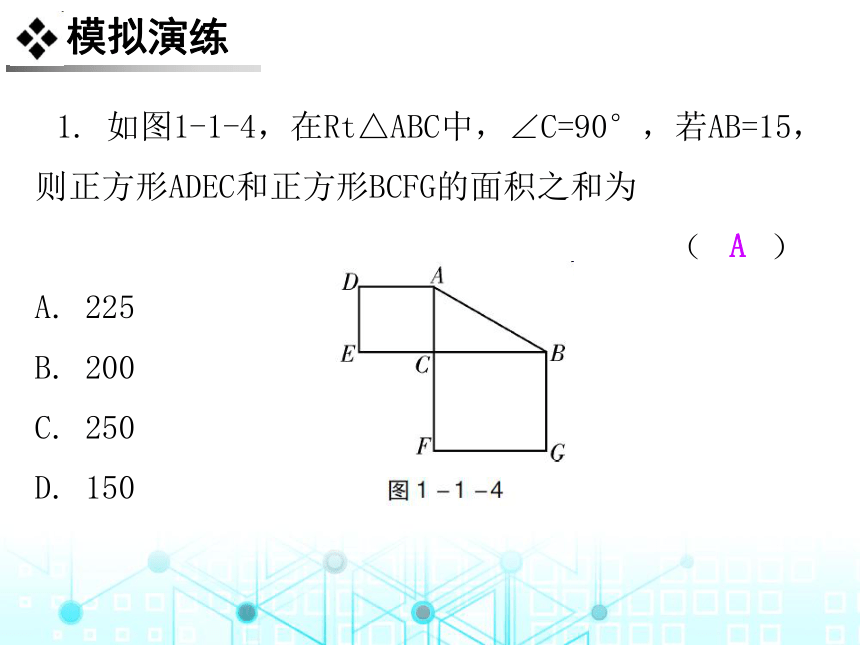
1. 如图1-1-4,在Rt△ABC中,∠C=90°,若AB=15,则正方形ADEC和正方形BCFG的面积之和为
( )
A. 225
B. 200
C. 250
D. 150
A
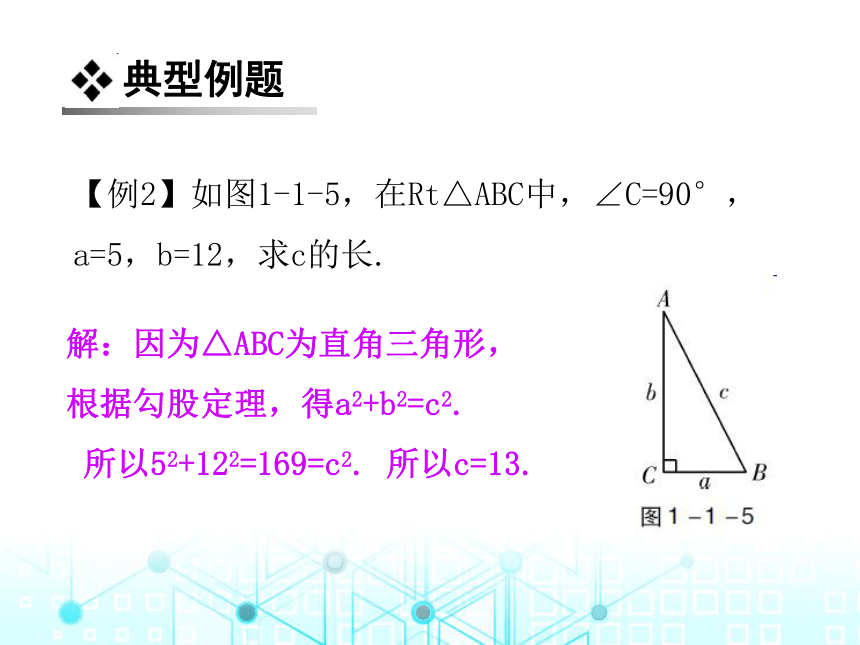
【例2】如图1-1-5,在Rt△ABC中,∠C=90°,a=5,b=12,求c的长.
解:因为△ABC为直角三角形,根据勾股定理,得a2+b2=c2.
所以52+122=169=c2. 所以c=13.
典型例题
模拟演练
2. 如图1-1-6,在Rt△ABC中,∠C=90°,BC=15,AB=25,求AC的长.
解:因为△ABC为直角三角形,
根据勾股定理,得AC2+BC2=AB2.
所以AC2=AB2-BC2=252-152=400.
所以AC=20.
新知2:勾股定理的验证
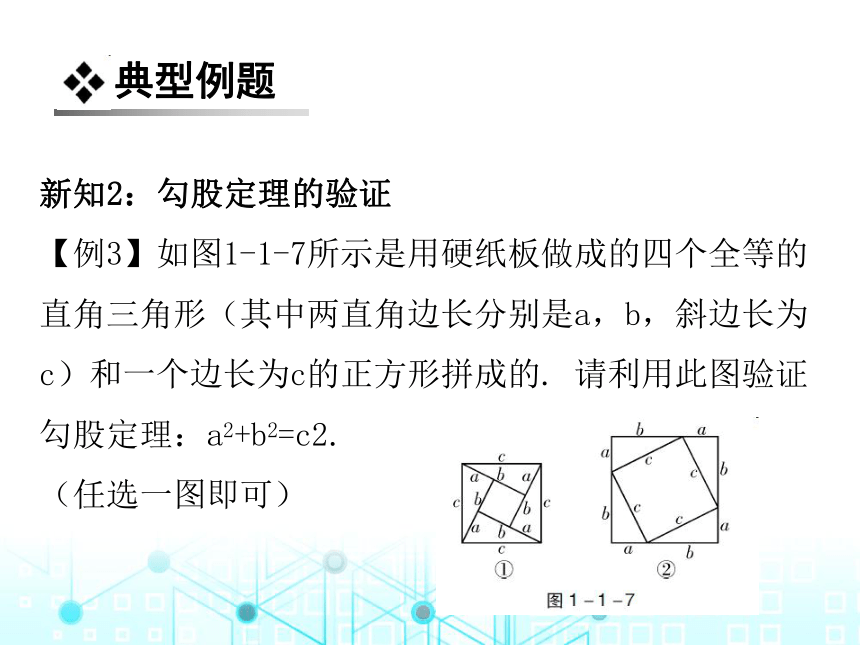
【例3】如图1-1-7所示是用硬纸板做成的四个全等的直角三角形(其中两直角边长分别是a,b,斜边长为c)和一个边长为c的正方形拼成的. 请利用此图验证勾股定理:a2+b2=c2.
(任选一图即可)
典型例题
解:选用图1-1-7①. 因为S大正方形=c2,
又S大正方形=4S△+S小正方形=4× ab+(b-a)2,
所以c2=4× ab+(b-a)2=a2+b2.
选用图1-1-7②.
因为S大正方形=(a+b)2,又S大正方形=4S△+S小正方形
=4× ab+c2,所以(a+b)2=4× ab+c2,
即a2+b2+2ab=c2+2ab.所以a2+b2=c2.
模拟演练
3. 做8个全等的直角三角形,设它们的两条直角边长分别为a,b,斜边长为c,再做3个边长分别为a,b,c的正方形,把它们按图1-1-8①和②所示的方式拼成两个正方形. 利用两个正方形的面积相等来验证勾股定理:a2+b2=c2.
解:由图1-1-8①可知大正方形的边长为a+b,则面积为(a+b)2;
图1-1-8②中把大正方形的面积分成了四部分,分别是:边长为a的正方形,边长为b的正方形,还有两个长为b,宽为a的长方形,则面积为a2+b2+2ab.
根据面积相等,得(a+b)2=a2+b2+2ab.
由图1-1-8①可得(a+b)2=c2+4× ab=c2+2ab.
所以a2+b2=c2.
新知3:勾股定理的简单应用
【例4】如图1-1-9,已知一根长8 m的竹竿在离地面3 m处断裂,竹竿顶部抵着地面,则此时竹竿的顶部与底部的距离为__________m.
4
典型例题
模拟演练
4. 如图1-1-10,有一羽毛球场地是长方形,已知AB=8 m,AD=6 m,若你要从A走到C,则至少走( )
A. 14 m
B. 12 m
C. 10 m
D. 9 m
C
分层训练
【A组】
1. 直角三角形两条直角边的长分别为3和4,则斜边长为 ( )
A. 4 B. 5 C. 6 D. 10
B
2. 如图1-1-11所示是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若最大正方形G的边长是6 cm,则正方形A,B,C,D,E,F,G的面积之和是 ( )
A. 18 cm2
B. 36 cm2
C. 72 cm2
D. 108 cm2
D
3. 下列选项中,不能用来证明勾股定理的是( )
D
4. 如果梯子的底端离建筑物5 m,那么13 m长的梯子可以到达建筑物的高度是 ( )
A. 12 m B. 13 m
C. 14 m D. 15 m
A
5. 一个直角三角形的三边长的平方和为200,则斜边长为__________.
10
【B组】
6. 用四个边长均为a,b,c的直角三角板,拼成如图1-1-12所示的图形,则下列结论正确的是 ( )
A. c2=a2+b2
B. c2=a2+2ab+b2
C. c2=a2-2ab+b2
D. c2=(a+b)2
A
7. 历史上对勾股定理的一种验证法采用了如图
1-1-13所示图形,其中两个全等的直角三角形的边AE,EB在一条直线上. 验证中用到的面积相等关系是 ( )
A. S△EDA=S△CEB
B. S△EDA+S△CEB=S△CDE
C. S四边形CDAE=S四边形CDEB
D. S△EDA+S△CDE+S△CEB=S四边形ABCD
D
8. 你听说过亡羊补牢的故事吗?如图1-1-14,为了防止羊的再次丢失,小明的爸爸要在高0.9 m,宽
1.2 m的栅栏门的相对角顶点间加一块加固木板,这块木板的长度为__________.
1.5 m
【C组】
9. 如图1-1-15,为修通铁路凿通隧道AC,量出∠ACB=90°,AB=5 km,BC=4 km,若每天凿隧道0.15 km,则几天才能把隧道AC凿通?
解:因为∠ACB=90°,AB=5 km,
BC=4 km,
由AC2+BC2=AB2,
得AC=3(km).
3÷0.15=20(天).
答:20天才能把隧道AC凿通.
10. 如图1-1-16,在四边形ABCD中,∠BAD=90°,∠CBD=90°,AD=4,AB=3,BC=12,求以DC为边的正方形的面积.
解:因为∠BAD=90°,所以AD2+AB2=DB2.
所以32+42=DB2.所以DB=5.
因为∠CBD=90°,所以BD2+BC2=DC2.
所以52+122=DC2.
所以DC=13.
所以S正方形DCEF=DC2=132=169.
1 探索勾股定理
名师导学
A. 勾股定理:__________三角形两__________的平方等于__________的平方.
如图1-1-1,在Rt△ABC中,∠C=90°,两直角边长分别为a,b,斜边长为c,那么__________+__________=__________.
直角
直角边
斜边
a2
b2
c2
1. 如图1-1-2所示是边长为1的正方形网格,下面是勾股定理的探索与验证过程,请补充完整:
因为S1=__________,S2=__________,S3=__________,
所以S1+S2=S3,
即__________2+__________2=__________2.
4
9
13
AC
BC
AB
课堂讲练
新知1:勾股定理的定义
【例1】如图1-1-3,已知两正方形的面积分别是25和169,则字母B所代表的正方形的面积是 ( )
A. 12
B. 13
C. 144
D. 194
C
典型例题
模拟演练
1. 如图1-1-4,在Rt△ABC中,∠C=90°,若AB=15,则正方形ADEC和正方形BCFG的面积之和为
( )
A. 225
B. 200
C. 250
D. 150
A
【例2】如图1-1-5,在Rt△ABC中,∠C=90°,a=5,b=12,求c的长.
解:因为△ABC为直角三角形,根据勾股定理,得a2+b2=c2.
所以52+122=169=c2. 所以c=13.
典型例题
模拟演练
2. 如图1-1-6,在Rt△ABC中,∠C=90°,BC=15,AB=25,求AC的长.
解:因为△ABC为直角三角形,
根据勾股定理,得AC2+BC2=AB2.
所以AC2=AB2-BC2=252-152=400.
所以AC=20.
新知2:勾股定理的验证
【例3】如图1-1-7所示是用硬纸板做成的四个全等的直角三角形(其中两直角边长分别是a,b,斜边长为c)和一个边长为c的正方形拼成的. 请利用此图验证勾股定理:a2+b2=c2.
(任选一图即可)
典型例题
解:选用图1-1-7①. 因为S大正方形=c2,
又S大正方形=4S△+S小正方形=4× ab+(b-a)2,
所以c2=4× ab+(b-a)2=a2+b2.
选用图1-1-7②.
因为S大正方形=(a+b)2,又S大正方形=4S△+S小正方形
=4× ab+c2,所以(a+b)2=4× ab+c2,
即a2+b2+2ab=c2+2ab.所以a2+b2=c2.
模拟演练
3. 做8个全等的直角三角形,设它们的两条直角边长分别为a,b,斜边长为c,再做3个边长分别为a,b,c的正方形,把它们按图1-1-8①和②所示的方式拼成两个正方形. 利用两个正方形的面积相等来验证勾股定理:a2+b2=c2.
解:由图1-1-8①可知大正方形的边长为a+b,则面积为(a+b)2;
图1-1-8②中把大正方形的面积分成了四部分,分别是:边长为a的正方形,边长为b的正方形,还有两个长为b,宽为a的长方形,则面积为a2+b2+2ab.
根据面积相等,得(a+b)2=a2+b2+2ab.
由图1-1-8①可得(a+b)2=c2+4× ab=c2+2ab.
所以a2+b2=c2.
新知3:勾股定理的简单应用
【例4】如图1-1-9,已知一根长8 m的竹竿在离地面3 m处断裂,竹竿顶部抵着地面,则此时竹竿的顶部与底部的距离为__________m.
4
典型例题
模拟演练
4. 如图1-1-10,有一羽毛球场地是长方形,已知AB=8 m,AD=6 m,若你要从A走到C,则至少走( )
A. 14 m
B. 12 m
C. 10 m
D. 9 m
C
分层训练
【A组】
1. 直角三角形两条直角边的长分别为3和4,则斜边长为 ( )
A. 4 B. 5 C. 6 D. 10
B
2. 如图1-1-11所示是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若最大正方形G的边长是6 cm,则正方形A,B,C,D,E,F,G的面积之和是 ( )
A. 18 cm2
B. 36 cm2
C. 72 cm2
D. 108 cm2
D
3. 下列选项中,不能用来证明勾股定理的是( )
D
4. 如果梯子的底端离建筑物5 m,那么13 m长的梯子可以到达建筑物的高度是 ( )
A. 12 m B. 13 m
C. 14 m D. 15 m
A
5. 一个直角三角形的三边长的平方和为200,则斜边长为__________.
10
【B组】
6. 用四个边长均为a,b,c的直角三角板,拼成如图1-1-12所示的图形,则下列结论正确的是 ( )
A. c2=a2+b2
B. c2=a2+2ab+b2
C. c2=a2-2ab+b2
D. c2=(a+b)2
A
7. 历史上对勾股定理的一种验证法采用了如图
1-1-13所示图形,其中两个全等的直角三角形的边AE,EB在一条直线上. 验证中用到的面积相等关系是 ( )
A. S△EDA=S△CEB
B. S△EDA+S△CEB=S△CDE
C. S四边形CDAE=S四边形CDEB
D. S△EDA+S△CDE+S△CEB=S四边形ABCD
D
8. 你听说过亡羊补牢的故事吗?如图1-1-14,为了防止羊的再次丢失,小明的爸爸要在高0.9 m,宽
1.2 m的栅栏门的相对角顶点间加一块加固木板,这块木板的长度为__________.
1.5 m
【C组】
9. 如图1-1-15,为修通铁路凿通隧道AC,量出∠ACB=90°,AB=5 km,BC=4 km,若每天凿隧道0.15 km,则几天才能把隧道AC凿通?
解:因为∠ACB=90°,AB=5 km,
BC=4 km,
由AC2+BC2=AB2,
得AC=3(km).
3÷0.15=20(天).
答:20天才能把隧道AC凿通.
10. 如图1-1-16,在四边形ABCD中,∠BAD=90°,∠CBD=90°,AD=4,AB=3,BC=12,求以DC为边的正方形的面积.
解:因为∠BAD=90°,所以AD2+AB2=DB2.
所以32+42=DB2.所以DB=5.
因为∠CBD=90°,所以BD2+BC2=DC2.
所以52+122=DC2.
所以DC=13.
所以S正方形DCEF=DC2=132=169.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
