人教版高一物理必修一课件4.7用牛顿运动定律解决问题(二)(共25张PPT)
文档属性
| 名称 | 人教版高一物理必修一课件4.7用牛顿运动定律解决问题(二)(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-08-23 20:36:25 | ||
图片预览







文档简介
(共25张PPT)
第四章
牛顿运动定律
牛顿第一定律
惯性定律,惯性
反映物体在不受力时的运动规律
牛顿第二定律
F=ma
反映了物体受力时力和运动的关系
牛顿第三定律
F=-F’
(作用力和反作用力定律)
反映了物体之间的相互作用规律
牛顿运动定律
复习
两类基本问题
受力情况
运动情况
a
牛顿第二定律F=ma
运动学公式
本节导航
1、共点力的平衡条件
2、超重和失重
3、从动力学看自由落体运动
1、共点力的平衡条件
物体所受各力共同作用在同一点上,或虽然不作用在同一点上,但它们的延长线(力的作用线)相交于一点,这几个力叫做共点力。
C
A
B
O
F1
F2
F3
G
F1
F2
θ
能简化成质点的物体受到的各个力可视为共点力
共点力?
静止状态或匀速直线运动状态,叫做平衡状态。
平衡状态?
共点力的平衡条件?
由牛顿第一定律和牛顿第二定律知:物体不受力或合力为零时将保持静止状态或匀速直线运动状态——平衡状态。共点力下平衡的条件是合力等于零即:F合=0。
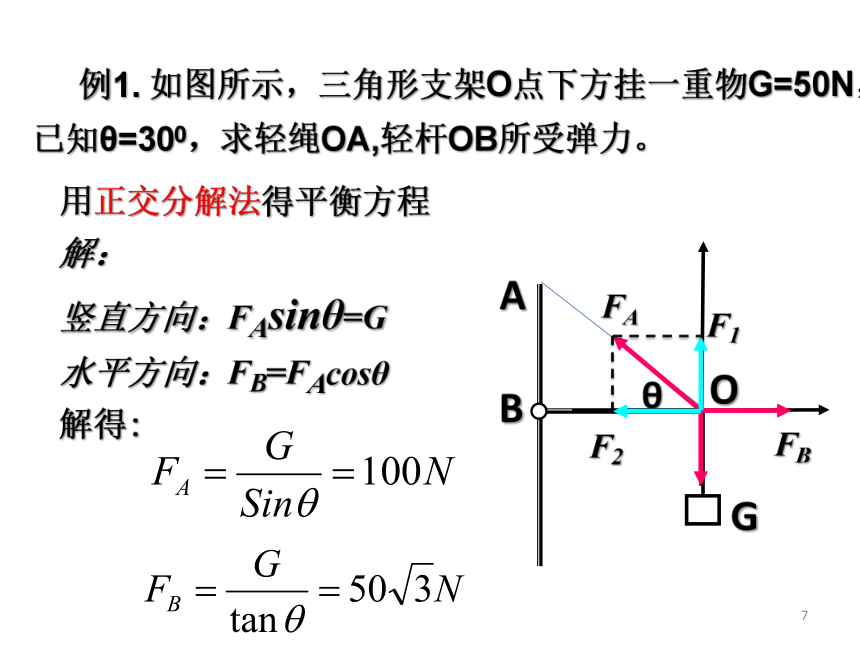
用正交分解法得平衡方程
解:
竖直方向:FAsinθ=G
水平方向:FB=FAcosθ
解得:
O
G
θ
B
A
FA
F1
F2
例1.
如图所示,三角形支架O点下方挂一重物G=50N,已知θ=300,求轻绳OA,轻杆OB所受弹力。
FB
O
G
θ
B
A
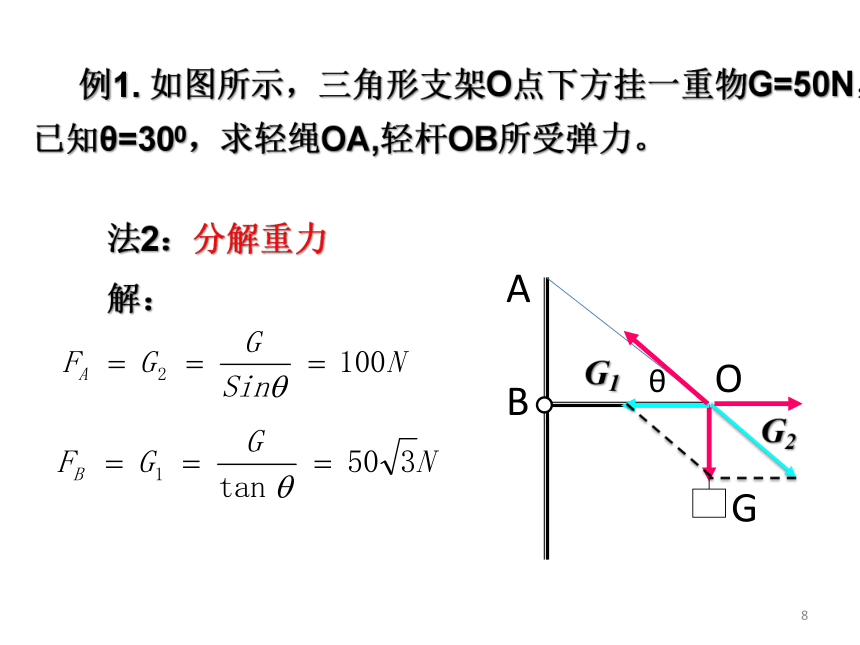
法2:分解重力
解:
G1
G2
例1.
如图所示,三角形支架O点下方挂一重物G=50N,已知θ=300,求轻绳OA,轻杆OB所受弹力。
2、超重和失重
生活实例——电梯情景
向上做加速运动
G
v
a
超重:物体对支持物的压力(物体对悬挂物的拉力)大于物体所受重力的现象。
现象:秤的读数大于物体所受重力
向上做减速运动
G
v
a
失重:物体对支持物的压力(物体对悬挂物的拉力)小于物体所受重力的现象。
现象:秤的读数小于物体所受重力
拓展:
实重:地球作用于物体的重力,通常始终存在且不变.
视重:物体对水平支持物的压力或悬挂物的拉力。
超重和失重产生的条件
二
加速度(a
↓)向下
失重
超重和失重与哪个运动量有关呢?速度还是加速度呢?
思考?
一
加速度(a
↑)向上
超重
现象:加速上升或减速下降
现象:加速下降或减速上升
只与a的方向有关,与V的方向无关。
加速上升过程
N
G
v
a
例:在升降机(电梯)中测人的体重,已知人质量为40kg,当升降机以2.5m/s2的加速度匀加速上升,体重计的示数是多少?(g取10
m/s2)
超重
电梯上升情景:
有向上的加速度
N=G+ma
F合=N-G=ma
N=mg+ma
=(40×10+40×2.5)N
=500N
体重计的示数:
50kg
v
N
G
失重
减速上升过程
a
例:在升降机(电梯)中测人的体重,已知人质量为40kg,当升降机以2.5m/s2的加速度匀减速上升,测力计的示数是多少?(g取10
m/s2)
有向下的加速度
N=G-ma
F合=G-N=ma
N
=mg-ma
=(40×10-40×2.5)N
=300N
体重计的示数:
30kg
如果升降机在静止时,悬挂升降机的钢索突然断裂,升降机自由下落,体重计的示数又是多少?
(g取10
m/s2)
G
v
g
思考?
结论:竖直向下的加速度a=g,物体对支持物、悬挂物完全没有作用力,这种现象叫完全失重。
g
v
G
向下具有重力加速度
N=0
G-N=ma
a=g
G=mg
N
小
结
特例:完全失重:(a=g)
超重与失重
重力始终不变
现象:F压(F拉)>
G
条件:a
超重
现象:
F压(F拉)<
G
条件:
a
失重
课堂练习
1.关于超重与失重,下列说法中正确的是
(
)
A.超重就是物体的重力增加了
B.完全失重就是物体的重力一点都没有了
C.
体操运动员双手握住单杠吊在空中不动时
处于失重状态
D.
蹦床运动员在空中上升和下落过程中
都处于失重状态
D
3、从动力学看落体运动
(1)自由落体运动定义:物体只在重力作用下从静止开始下落的运动。
(2)自由落体加速度:
F合=G=mg
a方向竖直向下
自由落体运动
G
v0=0
两个条件:初速度为0;只受重力的作用。
(1)竖直上抛运动定义:物体以一定的初速度竖直向上抛出后只在重力作用下的运动。
(2)竖直上抛运动加速度F合
=G=mg
a方向竖直向下
G
V0
竖直上抛运动
自由落体运动
两个条件:初速度竖直向上;只受重力的作用。
P90例题3.以10m/s的速度从地面竖直向上抛出一个物体,空气的阻力可以忽略,分别计算0.6s、1.6s后物体的位置(g取10m/s2)。
解:根据匀变速直线运动位移与时间的关系:
初速度的方向与加速度的方向相反所以求得抛出0.6s后物体位于地面以上4.2m的位置,1.6s后位于地面以上3.2m的位置。
练习:从塔上以20m/s的初速度竖直向上抛一个石子,不考虑空气阻力,求5s末石子速度和5s内石子位移。(g=10m/s2)。
解:以向上方向为正方向。
v0
x正
x
vt
第四章
牛顿运动定律
牛顿第一定律
惯性定律,惯性
反映物体在不受力时的运动规律
牛顿第二定律
F=ma
反映了物体受力时力和运动的关系
牛顿第三定律
F=-F’
(作用力和反作用力定律)
反映了物体之间的相互作用规律
牛顿运动定律
复习
两类基本问题
受力情况
运动情况
a
牛顿第二定律F=ma
运动学公式
本节导航
1、共点力的平衡条件
2、超重和失重
3、从动力学看自由落体运动
1、共点力的平衡条件
物体所受各力共同作用在同一点上,或虽然不作用在同一点上,但它们的延长线(力的作用线)相交于一点,这几个力叫做共点力。
C
A
B
O
F1
F2
F3
G
F1
F2
θ
能简化成质点的物体受到的各个力可视为共点力
共点力?
静止状态或匀速直线运动状态,叫做平衡状态。
平衡状态?
共点力的平衡条件?
由牛顿第一定律和牛顿第二定律知:物体不受力或合力为零时将保持静止状态或匀速直线运动状态——平衡状态。共点力下平衡的条件是合力等于零即:F合=0。
用正交分解法得平衡方程
解:
竖直方向:FAsinθ=G
水平方向:FB=FAcosθ
解得:
O
G
θ
B
A
FA
F1
F2
例1.
如图所示,三角形支架O点下方挂一重物G=50N,已知θ=300,求轻绳OA,轻杆OB所受弹力。
FB
O
G
θ
B
A
法2:分解重力
解:
G1
G2
例1.
如图所示,三角形支架O点下方挂一重物G=50N,已知θ=300,求轻绳OA,轻杆OB所受弹力。
2、超重和失重
生活实例——电梯情景
向上做加速运动
G
v
a
超重:物体对支持物的压力(物体对悬挂物的拉力)大于物体所受重力的现象。
现象:秤的读数大于物体所受重力
向上做减速运动
G
v
a
失重:物体对支持物的压力(物体对悬挂物的拉力)小于物体所受重力的现象。
现象:秤的读数小于物体所受重力
拓展:
实重:地球作用于物体的重力,通常始终存在且不变.
视重:物体对水平支持物的压力或悬挂物的拉力。
超重和失重产生的条件
二
加速度(a
↓)向下
失重
超重和失重与哪个运动量有关呢?速度还是加速度呢?
思考?
一
加速度(a
↑)向上
超重
现象:加速上升或减速下降
现象:加速下降或减速上升
只与a的方向有关,与V的方向无关。
加速上升过程
N
G
v
a
例:在升降机(电梯)中测人的体重,已知人质量为40kg,当升降机以2.5m/s2的加速度匀加速上升,体重计的示数是多少?(g取10
m/s2)
超重
电梯上升情景:
有向上的加速度
N=G+ma
F合=N-G=ma
N=mg+ma
=(40×10+40×2.5)N
=500N
体重计的示数:
50kg
v
N
G
失重
减速上升过程
a
例:在升降机(电梯)中测人的体重,已知人质量为40kg,当升降机以2.5m/s2的加速度匀减速上升,测力计的示数是多少?(g取10
m/s2)
有向下的加速度
N=G-ma
F合=G-N=ma
N
=mg-ma
=(40×10-40×2.5)N
=300N
体重计的示数:
30kg
如果升降机在静止时,悬挂升降机的钢索突然断裂,升降机自由下落,体重计的示数又是多少?
(g取10
m/s2)
G
v
g
思考?
结论:竖直向下的加速度a=g,物体对支持物、悬挂物完全没有作用力,这种现象叫完全失重。
g
v
G
向下具有重力加速度
N=0
G-N=ma
a=g
G=mg
N
小
结
特例:完全失重:(a=g)
超重与失重
重力始终不变
现象:F压(F拉)>
G
条件:a
超重
现象:
F压(F拉)<
G
条件:
a
失重
课堂练习
1.关于超重与失重,下列说法中正确的是
(
)
A.超重就是物体的重力增加了
B.完全失重就是物体的重力一点都没有了
C.
体操运动员双手握住单杠吊在空中不动时
处于失重状态
D.
蹦床运动员在空中上升和下落过程中
都处于失重状态
D
3、从动力学看落体运动
(1)自由落体运动定义:物体只在重力作用下从静止开始下落的运动。
(2)自由落体加速度:
F合=G=mg
a方向竖直向下
自由落体运动
G
v0=0
两个条件:初速度为0;只受重力的作用。
(1)竖直上抛运动定义:物体以一定的初速度竖直向上抛出后只在重力作用下的运动。
(2)竖直上抛运动加速度F合
=G=mg
a方向竖直向下
G
V0
竖直上抛运动
自由落体运动
两个条件:初速度竖直向上;只受重力的作用。
P90例题3.以10m/s的速度从地面竖直向上抛出一个物体,空气的阻力可以忽略,分别计算0.6s、1.6s后物体的位置(g取10m/s2)。
解:根据匀变速直线运动位移与时间的关系:
初速度的方向与加速度的方向相反所以求得抛出0.6s后物体位于地面以上4.2m的位置,1.6s后位于地面以上3.2m的位置。
练习:从塔上以20m/s的初速度竖直向上抛一个石子,不考虑空气阻力,求5s末石子速度和5s内石子位移。(g=10m/s2)。
解:以向上方向为正方向。
v0
x正
x
vt
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
