人教版八年级数学上册14.2.1平方差公式课件(共22张PPT)
文档属性
| 名称 | 人教版八年级数学上册14.2.1平方差公式课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 997.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-23 20:47:57 | ||
图片预览








文档简介
(共22张PPT)
14.2.1平方差公式
(a+b)(a-b)=?
计算下列多项式的积,你能发现什么规律?
(1)
(x+1)(x-1)=
(2)
(m+2)(m-2)=
(3)
(2x+1)(2x-1)=
x2
-x
+x
-1
m2
-2m
+2m
-4
(2x)2
-2x
+2x
-1
x2
=
=
-1
m2
-4
=
4x2
-1
我们再来计算
(a+b)(a?b),有
(a+b)(a?b)=
ab
a2
?
+
ab
b2
=
a2
?
b2
即:
(a+b)(a?b)=
a2
b2
?
?
(a+b)(a?b)=
a2?b2
两数和与这两数差的积,
等于
这两数的平方差.
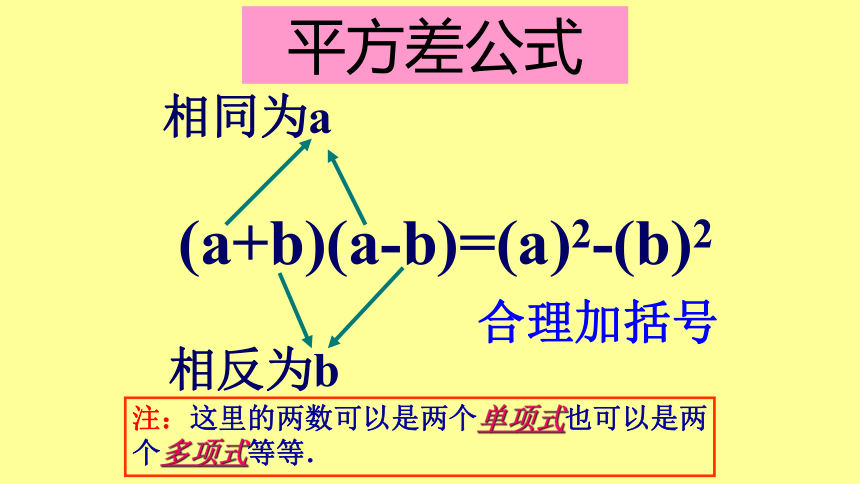
平方差公式
(a+b)(a-b)=(a)2-(b)2
相同为a
相反为b
合理加括号
平方差公式
注:这里的两数可以是两个单项式也可以是两个多项式等等.
运用公式的窍门:
1.先找出相同的项和相反的项,
相同的项看作公式中的a,
相反的项看作公式中的b
;
2.
再写成两项和乘以两项差的形式;
3.然后可以运用公式写出,即用
相同项的平方减去相反项的平方。
判断下列式子是否可用平方差公式。
(1)(-a+b)(a+b)
(2)
(-a+b)(a-b)
(3)(a+b)(a-c)
(4)(2+a)(a-2)
(5)
(1-x)(-x-1)
(6)(-4k3+3y2)(-4k3-3y2)
是
否
是
是
是
否
例1
运用平方差公式计算:
(1)
(3x+2)(3x
?
2)
(2)
(b+2a)(2a
?
b)
(3)
(?
x+2y)(?
x
?
2y)
分析:在(1)中,可以把3x看成a,2看成b,即
(1)
(3x+2)(3x
?
2)=
(
a+b)
(
a
?
b)
=
a2
b2
?
(3x)2
?
22
解:
(1)
(3x+2)(3x
?
2)=
?
22
(3x)2
?
9x2
=
4
例1
运用平方差公式计算:
(1)
(3x+2)(3x
?
2)
(2)
(b+2a)(2a
?
b)
(3)
(?
x+2y)(?
x
?
2y)
分析:在(2)中,可以把(
)看成a,
( )看成b
解:
(2)
(b+2a)(2a
?
b)=
?
b2
(2a)2
?
4a2
=
(2a+b)(2a
?
b)
=
b2
2a
b
例1
运用平方差公式计算:
(1)
(3x+2)(3x
?
2)
(2)
(b+2a)(2a
?
b)
(3)
(?
x+2y)(?
x
?
2y)
分析:在(3)中,可以把(
)看成a,
( )看成b
解:
(3)
(?
x+2y)(?
x
?
2y)=
?
(2y)2
(?
x)2
?
x2
=
4y2
?
x
2y
你还有其它的计算方法吗?
⑴
(a+1)(a-1)=
⑵
(3+x)(3-x)=
⑶
(a+2b)(a-2b)=
⑷
(3x+5y)(3x-5y)=
⑸
(10s-3t)(10s+3t)=
a2-1
9-x2
a2-(2b)2
=a2-4b2
(3x)2-(5y)2
=9x2-25y2
(10s)2-(3t)2
=100s2-9t2
(6)(?3x+2)(?3x?2)
=9x2-4
(8)(?3x+y)(3x+y)
(7)(?4a+3)(?4a?3)
(9)(y?x)(?x?y)
=16a2-9
=9x2-y2
=x2-y2
(10)(-m+n)(-m-n)=
(-m)2-n2
=m2-n2
(6)(?3x+2)(?3x?2)
(7)(?4a+3)(?4a?3)
例2:计算
(1)102×98
(2)
(y+2)(y-2)-(y-1)(y+5)
(1)解:原式=(100+2)(100-2)
=1002-22
=10000-4
=9996
例2:计算
(1)102×98
(2)
(y+2)(y-2)-(y-1)(y+5)
(2)解:原式=y2-4-(y2+4y-5)
=y2-4-y2-4y+5
=-4y+1
运用平方差公式计算:P108
(1)
(a+3b)(a-3b)
(2)
(3+2a)(-3+2a)
(3)
(3x+4)
(3x-4)
–
(2x+3)
(3x-2)
解:
(1)
(a+3b)(a-3b)=
?
(3b)2
a2
?
a2
=
9b2
(2)
(3+2a)(-3+2a)=
?
32
(2a)2
?
4a2
=
(2a+3)(2a-3)
=
9
(3)
(3x+4)(3x-4)-
(2x+3)(3x-2)
=
9x2-
42
-(6x2+5x-6)
=
9x2-16-6x2-5x+6
=
3x2-5x-10
明确哪个是
a
,
哪个是
b.再动笔
(4)1992×2008
(1)1992×2008
=(2000
?8)
×(2000+8
)
=20002
?82
=4000
000?64
=3
999
936
解:
(5)996×1004
(2)996×1004
=(1000
?4)
×(1000+4
)
=10002
?42
=1000
000?16
=999
984
(1)
(x+3)(
)=x2-9
(2)
(-1-2x)(
2x-1)=
(3)
(m+n)(
)=n2-m2
(4)
(
)(-y-1)=1-y2
(5)
(-3a2+2b2)(
)=9a4-4b4
X-3
1-4x2
n-m
-1+y
-3a2-2b2
(1)(x+y)(x-y)(x2+y2)
解:原式
=(x2-y2)(x2+y2)
=x4-y4
(2)
(x-y)(x+y)(x2+y2)(x4+y4)(x8+y8)
解:原式=
(x2-y2)(x2+y2)(x4+y4)(x8+y8)
=(x4-y4)
(x4+y4)(x8+y8)
=(x8-y8
)(x8+y8)
=x16-y16
(3)
(3a+b+c)(3a+b-c)
解:原式=[(3a+b)
+c][(3a+b)
-c]
=(3a+b)2-c2
=9a2+6ab+b2-c2
我学会了平方差公式,知道了平方差公式的特点
我学会了用几何方法验证平方差公式,让我体会到了数形结合的数学思想
我还找到了一些运用平方公式的小窍门
这节课你有哪些收获?
如左下图,边长为a的大正方形中有一个边长为b的小正方形.
(1)图中阴影部分的面积为________.
(2)将阴影部分拼成右图的一个长方形,这个长
方形的长是____,宽是____,面积是_________.
(3)比较(1)(2)的结果即可得到______________.
(a+b)(a-b)=a2-b2
有趣的数学
14.2.1平方差公式
(a+b)(a-b)=?
计算下列多项式的积,你能发现什么规律?
(1)
(x+1)(x-1)=
(2)
(m+2)(m-2)=
(3)
(2x+1)(2x-1)=
x2
-x
+x
-1
m2
-2m
+2m
-4
(2x)2
-2x
+2x
-1
x2
=
=
-1
m2
-4
=
4x2
-1
我们再来计算
(a+b)(a?b),有
(a+b)(a?b)=
ab
a2
?
+
ab
b2
=
a2
?
b2
即:
(a+b)(a?b)=
a2
b2
?
?
(a+b)(a?b)=
a2?b2
两数和与这两数差的积,
等于
这两数的平方差.
平方差公式
(a+b)(a-b)=(a)2-(b)2
相同为a
相反为b
合理加括号
平方差公式
注:这里的两数可以是两个单项式也可以是两个多项式等等.
运用公式的窍门:
1.先找出相同的项和相反的项,
相同的项看作公式中的a,
相反的项看作公式中的b
;
2.
再写成两项和乘以两项差的形式;
3.然后可以运用公式写出,即用
相同项的平方减去相反项的平方。
判断下列式子是否可用平方差公式。
(1)(-a+b)(a+b)
(2)
(-a+b)(a-b)
(3)(a+b)(a-c)
(4)(2+a)(a-2)
(5)
(1-x)(-x-1)
(6)(-4k3+3y2)(-4k3-3y2)
是
否
是
是
是
否
例1
运用平方差公式计算:
(1)
(3x+2)(3x
?
2)
(2)
(b+2a)(2a
?
b)
(3)
(?
x+2y)(?
x
?
2y)
分析:在(1)中,可以把3x看成a,2看成b,即
(1)
(3x+2)(3x
?
2)=
(
a+b)
(
a
?
b)
=
a2
b2
?
(3x)2
?
22
解:
(1)
(3x+2)(3x
?
2)=
?
22
(3x)2
?
9x2
=
4
例1
运用平方差公式计算:
(1)
(3x+2)(3x
?
2)
(2)
(b+2a)(2a
?
b)
(3)
(?
x+2y)(?
x
?
2y)
分析:在(2)中,可以把(
)看成a,
( )看成b
解:
(2)
(b+2a)(2a
?
b)=
?
b2
(2a)2
?
4a2
=
(2a+b)(2a
?
b)
=
b2
2a
b
例1
运用平方差公式计算:
(1)
(3x+2)(3x
?
2)
(2)
(b+2a)(2a
?
b)
(3)
(?
x+2y)(?
x
?
2y)
分析:在(3)中,可以把(
)看成a,
( )看成b
解:
(3)
(?
x+2y)(?
x
?
2y)=
?
(2y)2
(?
x)2
?
x2
=
4y2
?
x
2y
你还有其它的计算方法吗?
⑴
(a+1)(a-1)=
⑵
(3+x)(3-x)=
⑶
(a+2b)(a-2b)=
⑷
(3x+5y)(3x-5y)=
⑸
(10s-3t)(10s+3t)=
a2-1
9-x2
a2-(2b)2
=a2-4b2
(3x)2-(5y)2
=9x2-25y2
(10s)2-(3t)2
=100s2-9t2
(6)(?3x+2)(?3x?2)
=9x2-4
(8)(?3x+y)(3x+y)
(7)(?4a+3)(?4a?3)
(9)(y?x)(?x?y)
=16a2-9
=9x2-y2
=x2-y2
(10)(-m+n)(-m-n)=
(-m)2-n2
=m2-n2
(6)(?3x+2)(?3x?2)
(7)(?4a+3)(?4a?3)
例2:计算
(1)102×98
(2)
(y+2)(y-2)-(y-1)(y+5)
(1)解:原式=(100+2)(100-2)
=1002-22
=10000-4
=9996
例2:计算
(1)102×98
(2)
(y+2)(y-2)-(y-1)(y+5)
(2)解:原式=y2-4-(y2+4y-5)
=y2-4-y2-4y+5
=-4y+1
运用平方差公式计算:P108
(1)
(a+3b)(a-3b)
(2)
(3+2a)(-3+2a)
(3)
(3x+4)
(3x-4)
–
(2x+3)
(3x-2)
解:
(1)
(a+3b)(a-3b)=
?
(3b)2
a2
?
a2
=
9b2
(2)
(3+2a)(-3+2a)=
?
32
(2a)2
?
4a2
=
(2a+3)(2a-3)
=
9
(3)
(3x+4)(3x-4)-
(2x+3)(3x-2)
=
9x2-
42
-(6x2+5x-6)
=
9x2-16-6x2-5x+6
=
3x2-5x-10
明确哪个是
a
,
哪个是
b.再动笔
(4)1992×2008
(1)1992×2008
=(2000
?8)
×(2000+8
)
=20002
?82
=4000
000?64
=3
999
936
解:
(5)996×1004
(2)996×1004
=(1000
?4)
×(1000+4
)
=10002
?42
=1000
000?16
=999
984
(1)
(x+3)(
)=x2-9
(2)
(-1-2x)(
2x-1)=
(3)
(m+n)(
)=n2-m2
(4)
(
)(-y-1)=1-y2
(5)
(-3a2+2b2)(
)=9a4-4b4
X-3
1-4x2
n-m
-1+y
-3a2-2b2
(1)(x+y)(x-y)(x2+y2)
解:原式
=(x2-y2)(x2+y2)
=x4-y4
(2)
(x-y)(x+y)(x2+y2)(x4+y4)(x8+y8)
解:原式=
(x2-y2)(x2+y2)(x4+y4)(x8+y8)
=(x4-y4)
(x4+y4)(x8+y8)
=(x8-y8
)(x8+y8)
=x16-y16
(3)
(3a+b+c)(3a+b-c)
解:原式=[(3a+b)
+c][(3a+b)
-c]
=(3a+b)2-c2
=9a2+6ab+b2-c2
我学会了平方差公式,知道了平方差公式的特点
我学会了用几何方法验证平方差公式,让我体会到了数形结合的数学思想
我还找到了一些运用平方公式的小窍门
这节课你有哪些收获?
如左下图,边长为a的大正方形中有一个边长为b的小正方形.
(1)图中阴影部分的面积为________.
(2)将阴影部分拼成右图的一个长方形,这个长
方形的长是____,宽是____,面积是_________.
(3)比较(1)(2)的结果即可得到______________.
(a+b)(a-b)=a2-b2
有趣的数学
