人教版八年级数学上册14.2.2 完全平方公式 课件(共28张PPT)
文档属性
| 名称 | 人教版八年级数学上册14.2.2 完全平方公式 课件(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-23 00:00:00 | ||
图片预览







文档简介
(共28张PPT)
用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加.
(a+b)(m+n)
=
am
+an
+bm
+bn
多项式的乘法
(a+b)2
(a-b)2
=
a2
+2ab+b2
=
a2
-
2ab+b2
=
a2
+ab
+ab
+b2
=
a2
-
ab
-
ab
+b2
=(a+b)
(a+b)
=(a-b)
(a-b)
整式的乘法
情景
&
导入
?
?
乘法公式
计算下列各题:
观察以上多项式的乘法,有什么特点?
完全平方公式的数学表达式:
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍。
(a+b)2=
a2
+b2
+2ab
(a-b)2=
a2
+b2
-
2ab
(a+b)2=
a2
+2ab+b2
(a-b)2=
a2
-
2ab+b2
整式的乘法
完全平方公式
请你尝试用文字概括这个结论。
运算形式
运算方法
(和或差、平方)
(平方和、加或减2倍积)
b
b
a
a
(a+b)?
a?
b?
ab
ab
+
+
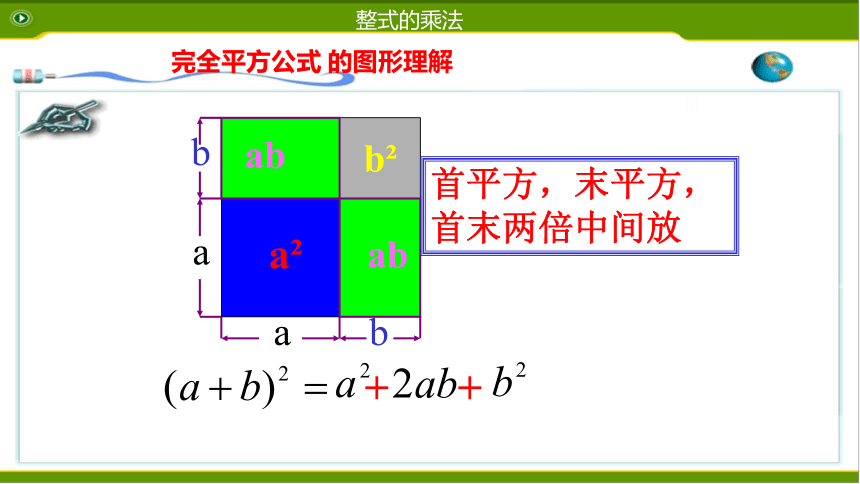
完全平方公式
的图形理解
整式的乘法
首平方,末平方,首末两倍中间放
a
a
b
b
(a-b)?
a?
ab
ab
b?
b
b
完全平方公式
的图形理解
整式的乘法
首平方,末平方,首末两倍中间放
公式特点:
4、公式中的字母a,b可以表示数,单项式和多项式。
(a+b)2=
a2
+2ab+b2
(a-b)2=
a2
-
2ab+b2
1、积为二次三项式;
2、积中两项为两数的平方和;
3、另一项是两数积的2倍,且与乘式中间的符号相同。
首平方,末平方,首末两倍中间放
整式的乘法
完全平方公式
做一做:用两数和的完全平方公式计算(填空):
(a+1)2=(
)2+2(
)(
)+(
)2
=
_____________
(2)(2a+3b)2=(
)2+2(
)(
)+(
)2
=__________________
整式的乘法
完全平方公式
感受新知----试一试
a
1
a
1
a2+2a+1
2a
2a
3b
3b
4a2+12ab+9b2
下面各式的计算是否正确?如果不正确,应当怎样改正?
(x+y)2=x2
+y2
(2)(x
-y)2
=x2
-y2
(3)
(x
-y)2
=x2+2xy
+y2
(4)
(x+y)2
=x2
+xy
+y2
错
错
错
错
(x
+y)2
=x2+2xy
+y2
(x
-y)2
=x2
-2xy
+y2
(x
-y)2
=x2
-2xy
+y2
(x
+y)2
=x2+2xy
+y2
整式的乘法
完全平方公式
感受新知----试一试
例1
运用完全平方公式计算:
解:
(x+2y)2=
=x2
(1)(x+2y)2
(a
+b)2=
a2
+
2
ab
+
b2
x2
+2?x
?2y
+(2y)2
+4xy
+4y2
第十五章
整式的乘法
完全平方公式
感受新知----看一看
(2)(x-2y)2
解:
(x-2y)2=
x2
-2?x
?2y
+(2y)2
=x2
(a
-
b)2=
a2
-
2
ab
+
b2
-4xy
+4y2
例2、运用完全平方公式计算:
(1)
(
4a2
-
b2
)2
解:
(
4a2
-
b2)2
=(
)2-2(
)·(
)+(
)2
=16a4-8a2b2+b4
记清公式、代准数式、准确计算。
解题过程分3步:
4a2
4a2
b2
b2
第十五章
整式的乘法
完全平方公式
感受新知----看一看
=
x2
–
2xy2+4y4
+(2y2)2
(a
-
b)2
=
a2
-
2ab
+
b2
(2)
(
x
–
2y2)2
–
2
?(
x)
?(2y2)
(
x)2
解:(
x
–
2y2)2
=
整式的乘法
完全平方公式
感受新知----看一看
(3)
(3x-7y)2
=
(4)(2a2+3b)2=
整式的乘法
完全平方公式
感受新知----算一算
(1)
(2x+1)2
=
(5)(-2a2+b)2=
=4x2
+4x
+1
(2x)2
+2
×
2x
×1
+12
(2)
(3m?2n)2
=
(3m)2
-2×3m×2n
+(2n)2
=9m2
-12mn
+4n2
=4a4
+12a2b
+9b2
(3x)2
-2×3x×7y
+(7y)2
=9x2
-42xy
+49y2
(2a2)2
+2×2a2×3b
+(3b)2
(b-2a2)2=
b2
-2×b×(2a2)
+(2a)2
=b2
-4a2b
+4a2
运用完全平方公式计算:
(1)
1042
解:
1042
=
(100+4)2
=10000+800+16
=10816
(2)
99.992
解:
99.992
=
(100
–0.01)2
=10000
-2+0.0001
=9998.0001
整式的乘法
完全平方公式
感受新知---试一试
整式的乘法
完全平方公式
继续探索----试一试
如何运用完全平方公式使计算更简便
(1)
(-a+b)2
(2)
(-2m-1)2
(3)
(2x+5)(-2x-5)
(4)
(x+y-1)2
=
(b-a)2
=
-(2m+1)
2
=
(2m+1)2
=
-(2x+5)(2x+5)
=
-(2x+5)2
=
(x+y)-1
2
(1)
(6a+5b)2
=36a2+60ab+25b2
(2)
(4x-3y)2
=16x2-24xy+9y2
(3)
(2m-1)2
=4m2-4m+1
(4)
(-2m-1)2
=4m2+4m+1
整式的乘法
完全平方公式
熟练运用----算一算
2、(______)2
=9a2―(_______)+16b2
;
整式的乘法
完全平方公式
理解新知----算一算
1.(____-y4)2=_____-xy4
+_______
3.4a2-____+49=
(_______)2。
4.(a+b+c)2=[a+_________]2
=a2+___________+(
_____
)2
=a2+____________________
。
y8
3a-4b
24ab
28a
2a-7
(b+c)
2a(b+c)
b+c
b2+c2+2ab+2ac+2bc
1、代数式2xy-x2-y2=
(
)
A.(x-y)2
B.(-x-y)2
C.(y-x)2
D.-(x-y)2
D
2、如果x2-6xy+N是一个完全平方式,那么N为________
整式的乘法
完全平方公式
深入探索----算一算
3、如果4x2+mxy+9y2是一个完全平方式,那么m的值是____________
9y2
±12
整式的乘法
完全平方公式
深入探索----算一算
(a+b)2
_a2_b2
=______
(a-b)2+2ab=
______
公式变形
(a-b)2+4ab=
______
(a+b)2-4ab=_______
(a+b)2_2ab=
_____
2ab
a2
+b2
(a+b)2-(a-b)2=______
a2
+b2
4ab
(a-b)2
(a+b)2
整式的乘法
完全平方公式
深入探索----算一算
1、已知(a+b)2=11,ab=1,求(a-b)2的值.
2、若(x+y)2=9,(x-y)2=5,则xy=______
3、多项式
加上一个单项式后,使它成为一个整式的完全平方式,那么加上的单项式可以是__________
4、已知
(a+b)2=25
ab=3
则
a2+b2=___
5、已知:a+b=5,ab=-6,求下列各式的值
(1)(a+b)2
(2)a2+b2
6.
计算:4x(x-1)2+x(2x+5)·(5-2x)
7.
当x=2,y=-1时。求代数式
(x+y)(x-y)+(x-y)2-(x2-3xy)的值。
8.用简便的方法计算:
1.23452+0.76552+2.469×0.7655
整式的乘法
完全平方公式
深入探索----算一算
9.(1)(x+3)2-x2
(2)
(a+b+3)(a-b-3)
(3)(x+5)2-(x-2)(x-3)
10.运用乘法公式计算:
(1)
(x+2y-
)(x-2y+
)
11.已知
求下列式子的值:
整式的乘法
完全平方公式
深入探索----算一算
12.已知:a-b=5,ab=-6,求a2+b2的值
13.计算(a-b-3)(a-b+3)
14.二次三项式
是一个完全平方式,求m的值?
15.已知n为正整数,且
是一个完全平方数,你知道n的值吗?
整式的乘法
完全平方公式
熟练运用----算一算
整式的乘法
完全平方公式
感受新知----看一看
运用乘法公式计算
(1)(x+2y-3)(x+2y+3)
(2)(x+2y-3)(x-2y+3)
(3)(a+b+c)2
(1)
(2a+3)2
(2)
(b-3)2
(3)
(-2x-3y)2
(4)
(5)
(6)
(1-3x)(3x-1)
(7)
(a?b?3)(a?b+3)。
整式的乘法
完全平方公式
熟练运用----算一算
(a+b)2=
a2
+2ab+b2
(a-b)2=
a2
-
2ab+b2
1、完全平方公式:
2、注意:项数、符号、字母及其指数;
3、公式的逆向使用;
4、解题时常用结论:
(-a-b)2
=(a+b)2
(a-b)2
=(b-a)2
a2
+2ab+b2
=
(a+b)2
a2
-
2ab+b2=
(a-b)2
整式的乘法
完全平方公式
(1)
(
x
?
2y)2
;
(2)
(2xy+
x
)2
;
1、利用完全平方公式计算:
(n
+1)2
?
n2;
(-x-y)2.
整式的乘法
完全平方公式
熟练运用----算一算
通过这节课的学习你学到了什么
用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加.
(a+b)(m+n)
=
am
+an
+bm
+bn
多项式的乘法
(a+b)2
(a-b)2
=
a2
+2ab+b2
=
a2
-
2ab+b2
=
a2
+ab
+ab
+b2
=
a2
-
ab
-
ab
+b2
=(a+b)
(a+b)
=(a-b)
(a-b)
整式的乘法
情景
&
导入
?
?
乘法公式
计算下列各题:
观察以上多项式的乘法,有什么特点?
完全平方公式的数学表达式:
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍。
(a+b)2=
a2
+b2
+2ab
(a-b)2=
a2
+b2
-
2ab
(a+b)2=
a2
+2ab+b2
(a-b)2=
a2
-
2ab+b2
整式的乘法
完全平方公式
请你尝试用文字概括这个结论。
运算形式
运算方法
(和或差、平方)
(平方和、加或减2倍积)
b
b
a
a
(a+b)?
a?
b?
ab
ab
+
+
完全平方公式
的图形理解
整式的乘法
首平方,末平方,首末两倍中间放
a
a
b
b
(a-b)?
a?
ab
ab
b?
b
b
完全平方公式
的图形理解
整式的乘法
首平方,末平方,首末两倍中间放
公式特点:
4、公式中的字母a,b可以表示数,单项式和多项式。
(a+b)2=
a2
+2ab+b2
(a-b)2=
a2
-
2ab+b2
1、积为二次三项式;
2、积中两项为两数的平方和;
3、另一项是两数积的2倍,且与乘式中间的符号相同。
首平方,末平方,首末两倍中间放
整式的乘法
完全平方公式
做一做:用两数和的完全平方公式计算(填空):
(a+1)2=(
)2+2(
)(
)+(
)2
=
_____________
(2)(2a+3b)2=(
)2+2(
)(
)+(
)2
=__________________
整式的乘法
完全平方公式
感受新知----试一试
a
1
a
1
a2+2a+1
2a
2a
3b
3b
4a2+12ab+9b2
下面各式的计算是否正确?如果不正确,应当怎样改正?
(x+y)2=x2
+y2
(2)(x
-y)2
=x2
-y2
(3)
(x
-y)2
=x2+2xy
+y2
(4)
(x+y)2
=x2
+xy
+y2
错
错
错
错
(x
+y)2
=x2+2xy
+y2
(x
-y)2
=x2
-2xy
+y2
(x
-y)2
=x2
-2xy
+y2
(x
+y)2
=x2+2xy
+y2
整式的乘法
完全平方公式
感受新知----试一试
例1
运用完全平方公式计算:
解:
(x+2y)2=
=x2
(1)(x+2y)2
(a
+b)2=
a2
+
2
ab
+
b2
x2
+2?x
?2y
+(2y)2
+4xy
+4y2
第十五章
整式的乘法
完全平方公式
感受新知----看一看
(2)(x-2y)2
解:
(x-2y)2=
x2
-2?x
?2y
+(2y)2
=x2
(a
-
b)2=
a2
-
2
ab
+
b2
-4xy
+4y2
例2、运用完全平方公式计算:
(1)
(
4a2
-
b2
)2
解:
(
4a2
-
b2)2
=(
)2-2(
)·(
)+(
)2
=16a4-8a2b2+b4
记清公式、代准数式、准确计算。
解题过程分3步:
4a2
4a2
b2
b2
第十五章
整式的乘法
完全平方公式
感受新知----看一看
=
x2
–
2xy2+4y4
+(2y2)2
(a
-
b)2
=
a2
-
2ab
+
b2
(2)
(
x
–
2y2)2
–
2
?(
x)
?(2y2)
(
x)2
解:(
x
–
2y2)2
=
整式的乘法
完全平方公式
感受新知----看一看
(3)
(3x-7y)2
=
(4)(2a2+3b)2=
整式的乘法
完全平方公式
感受新知----算一算
(1)
(2x+1)2
=
(5)(-2a2+b)2=
=4x2
+4x
+1
(2x)2
+2
×
2x
×1
+12
(2)
(3m?2n)2
=
(3m)2
-2×3m×2n
+(2n)2
=9m2
-12mn
+4n2
=4a4
+12a2b
+9b2
(3x)2
-2×3x×7y
+(7y)2
=9x2
-42xy
+49y2
(2a2)2
+2×2a2×3b
+(3b)2
(b-2a2)2=
b2
-2×b×(2a2)
+(2a)2
=b2
-4a2b
+4a2
运用完全平方公式计算:
(1)
1042
解:
1042
=
(100+4)2
=10000+800+16
=10816
(2)
99.992
解:
99.992
=
(100
–0.01)2
=10000
-2+0.0001
=9998.0001
整式的乘法
完全平方公式
感受新知---试一试
整式的乘法
完全平方公式
继续探索----试一试
如何运用完全平方公式使计算更简便
(1)
(-a+b)2
(2)
(-2m-1)2
(3)
(2x+5)(-2x-5)
(4)
(x+y-1)2
=
(b-a)2
=
-(2m+1)
2
=
(2m+1)2
=
-(2x+5)(2x+5)
=
-(2x+5)2
=
(x+y)-1
2
(1)
(6a+5b)2
=36a2+60ab+25b2
(2)
(4x-3y)2
=16x2-24xy+9y2
(3)
(2m-1)2
=4m2-4m+1
(4)
(-2m-1)2
=4m2+4m+1
整式的乘法
完全平方公式
熟练运用----算一算
2、(______)2
=9a2―(_______)+16b2
;
整式的乘法
完全平方公式
理解新知----算一算
1.(____-y4)2=_____-xy4
+_______
3.4a2-____+49=
(_______)2。
4.(a+b+c)2=[a+_________]2
=a2+___________+(
_____
)2
=a2+____________________
。
y8
3a-4b
24ab
28a
2a-7
(b+c)
2a(b+c)
b+c
b2+c2+2ab+2ac+2bc
1、代数式2xy-x2-y2=
(
)
A.(x-y)2
B.(-x-y)2
C.(y-x)2
D.-(x-y)2
D
2、如果x2-6xy+N是一个完全平方式,那么N为________
整式的乘法
完全平方公式
深入探索----算一算
3、如果4x2+mxy+9y2是一个完全平方式,那么m的值是____________
9y2
±12
整式的乘法
完全平方公式
深入探索----算一算
(a+b)2
_a2_b2
=______
(a-b)2+2ab=
______
公式变形
(a-b)2+4ab=
______
(a+b)2-4ab=_______
(a+b)2_2ab=
_____
2ab
a2
+b2
(a+b)2-(a-b)2=______
a2
+b2
4ab
(a-b)2
(a+b)2
整式的乘法
完全平方公式
深入探索----算一算
1、已知(a+b)2=11,ab=1,求(a-b)2的值.
2、若(x+y)2=9,(x-y)2=5,则xy=______
3、多项式
加上一个单项式后,使它成为一个整式的完全平方式,那么加上的单项式可以是__________
4、已知
(a+b)2=25
ab=3
则
a2+b2=___
5、已知:a+b=5,ab=-6,求下列各式的值
(1)(a+b)2
(2)a2+b2
6.
计算:4x(x-1)2+x(2x+5)·(5-2x)
7.
当x=2,y=-1时。求代数式
(x+y)(x-y)+(x-y)2-(x2-3xy)的值。
8.用简便的方法计算:
1.23452+0.76552+2.469×0.7655
整式的乘法
完全平方公式
深入探索----算一算
9.(1)(x+3)2-x2
(2)
(a+b+3)(a-b-3)
(3)(x+5)2-(x-2)(x-3)
10.运用乘法公式计算:
(1)
(x+2y-
)(x-2y+
)
11.已知
求下列式子的值:
整式的乘法
完全平方公式
深入探索----算一算
12.已知:a-b=5,ab=-6,求a2+b2的值
13.计算(a-b-3)(a-b+3)
14.二次三项式
是一个完全平方式,求m的值?
15.已知n为正整数,且
是一个完全平方数,你知道n的值吗?
整式的乘法
完全平方公式
熟练运用----算一算
整式的乘法
完全平方公式
感受新知----看一看
运用乘法公式计算
(1)(x+2y-3)(x+2y+3)
(2)(x+2y-3)(x-2y+3)
(3)(a+b+c)2
(1)
(2a+3)2
(2)
(b-3)2
(3)
(-2x-3y)2
(4)
(5)
(6)
(1-3x)(3x-1)
(7)
(a?b?3)(a?b+3)。
整式的乘法
完全平方公式
熟练运用----算一算
(a+b)2=
a2
+2ab+b2
(a-b)2=
a2
-
2ab+b2
1、完全平方公式:
2、注意:项数、符号、字母及其指数;
3、公式的逆向使用;
4、解题时常用结论:
(-a-b)2
=(a+b)2
(a-b)2
=(b-a)2
a2
+2ab+b2
=
(a+b)2
a2
-
2ab+b2=
(a-b)2
整式的乘法
完全平方公式
(1)
(
x
?
2y)2
;
(2)
(2xy+
x
)2
;
1、利用完全平方公式计算:
(n
+1)2
?
n2;
(-x-y)2.
整式的乘法
完全平方公式
熟练运用----算一算
通过这节课的学习你学到了什么
