沪教版(上海)数学六年级上册 第一章 数的整除 (培优) 课件(15张PPT)
文档属性
| 名称 | 沪教版(上海)数学六年级上册 第一章 数的整除 (培优) 课件(15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 299.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-25 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
数的整除
知识要点
1.能被2整除的数的特征:
个位数字是0、2、4、6、8的整数.
2.能被5整除的数的特征:
个位数字是0或5的整数.
3.能被3(或9)整除的数的特征:
各个数字之和能被3(或9)整除.
4.能被4(或25)整除的数的特征:
末两位数能被4(或25)整除.
能被8(或125)整除的数的特征:
末三位数能被8(或125)整除.
知识要点
5.被11整除的数的特征是:
一个整数的奇数位上的数字之和与偶数位上的数字之和的差(大减小)是11的倍数.
6.能被7,11,
13整除的数的特征:
一个数的末三位与末三位以前的数字所组成的数的差能被7,11,
13整除。
典例精析
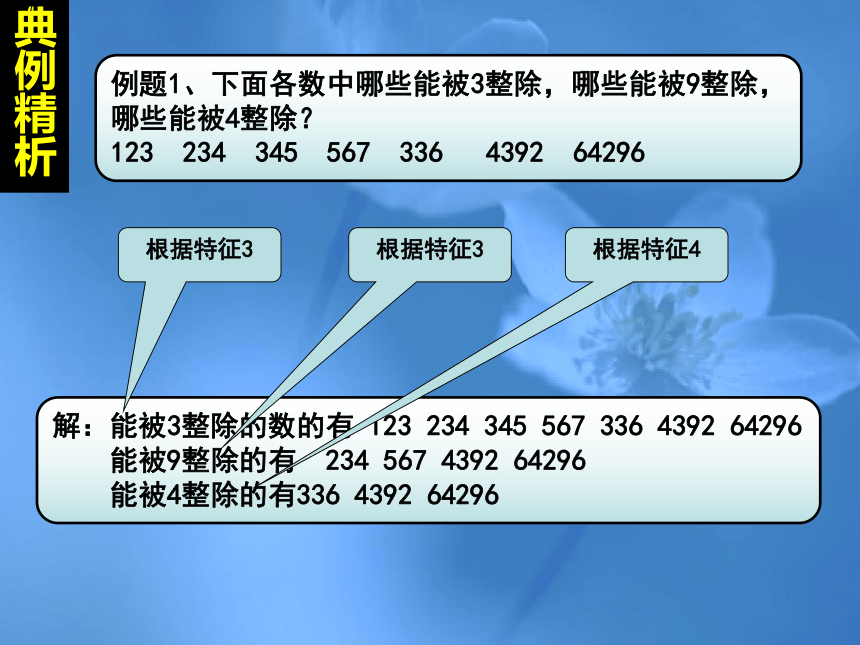
解:能被3整除的数的有
123
234
345
567
336
4392
64296
能被9整除的有
234
567
4392
64296
能被4整除的有336
4392
64296
例题1、下面各数中哪些能被3整除,哪些能被9整除,哪些能被4整除?
123
234
345
567
336
4392
64296
根据特征3
根据特征4
根据特征3
典例精析
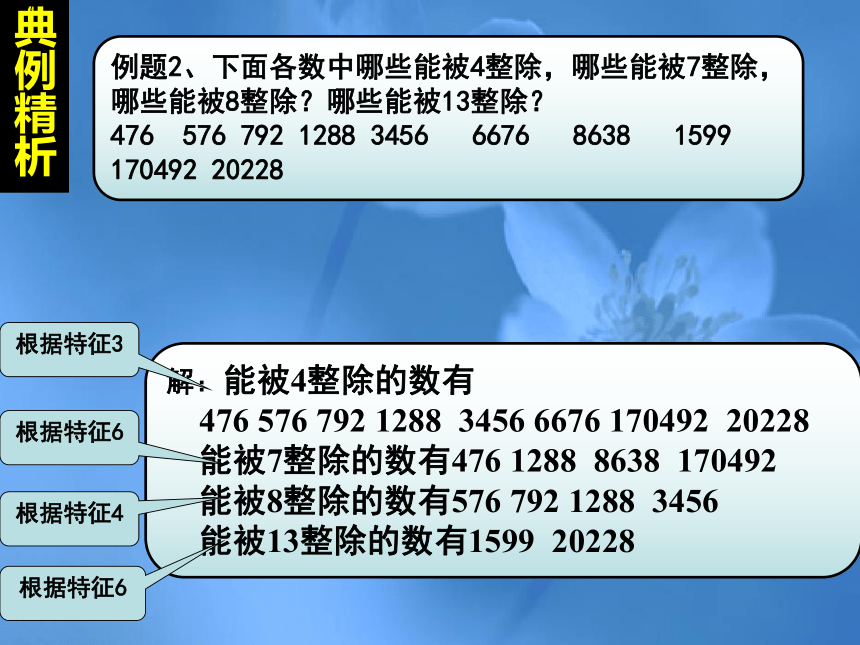
解:能被4整除的数有
476
576
792
1288
3456
6676
170492
20228
能被7整除的数有476
1288
8638
170492
能被8整除的数有576
792
1288
3456
能被13整除的数有1599
20228
例题2、下面各数中哪些能被4整除,哪些能被7整除,哪些能被8整除?哪些能被13整除?
476
576
792
1288
3456
6676
8638
1599
170492
20228
根据特征3
根据特征6
根据特征4
根据特征6
典例精析
解:∵
173a能被9整除,
∴
1+7+3+a=11+a能被9整除,∴
a=7;
∵
173a能被11整除,
∴(7+a)-(3+1)=3+a能被11整除,∴a=8;
∵
173a能被6整除,
∴a是偶数且1+7+3+a=11+a能被3整除,
∴
a=4;
∴综上所述:数学老师先后所取的三个数字的和是
7+8+4=19.
例题3、
173a是一个四位数,数学老师说:“我们把a取三个不同的数,所得的三个四位数,依次可以被9、11、6整除”。
问:这先后所取的三个数字的和是多少?
典例精析
解:
∵27ab能被2、5整除,
∴可以判定b=0。
又∵27ab又能被4整除,
∴可能是00,20,40,60,80.
∵又27ab能被9和3整除,可以判定a=0.
∴
27ab=2700.
例题4、一个四位数27ab能同时被2,3,4,5,9整除,则这个四位数是多少?
典例精析
解:∵
1x2x3x4x5能被11整除,
∴(1+2+3+4+5)-4x=15-4x能被11整除或者4x-15
能被11整除;
又∵x是大于等于0,小于等于9的整数,
∴只有
x=1满足条件。
∴这个整数为112131415。
例题5、已知1x2x3x4x5整数能被11整除,求所有满足这个条件的整数。
典例精析
解:因为65=5×13,又因为5和13互素,
所以
既能被5整除又能被13整除。
能被5整除,可以得出y=0
或5;当
y=0时,x=7
;当y=5
时,x=9;所以满足条件的六位数是917930
和919935.
例题6、已知
能被65整除,求满足条件的六位数
特征2
特征6
特征6
典例精析
解法一:设这个三位数是
,根据题意可知这个六位数
.因为
=0,所以
能被7,11,13整除。即任意三位数连写一次得到的一个六位数能被7,11,13整除.
例题7、任意三位数连写一次得到的一个六位数是否能被7,11,13整除?
特征6
例题8:
某数被2除余1,被3除余2,被4除余3,被5除余4,满足以上条件的数有多少个?最小的一个数是几?
解:这个数,加上1,就能同时被
2,3,4,5整除
2,3,4,5的最小公倍数为60
满足要求的最小的数为:60-1=59
这样的数有无数多个
59再加上60的整数倍,都满足要求
例如:59+60=119
59+60
2=179
典例精析
典例精析
解:
∵(
1625,1170)=5×13
(方法一)∵AB:1625÷65=25,BC:1170÷65=18
∴25+18+1=44
∴这条街道最少要安装44盏路灯.
(方法二)∵AB:1625÷65=25,
BC:1170÷65=18
∴(25+1)+(18+1)-1=44
∴这条街道最少要安装44盏路灯.
(方法三)∵AB+BC:
(1625+1170)÷65=43
∴43+1=44
∴这条街道最少要安装44盏路灯.
例题9.如图,街道ABC在B处拐弯,在街道的一侧要等距离安装路灯,并要求在A、B、C处各安装一盏路灯,问这条街道最少要安装多少盏路灯?
小试牛刀
练习:
动物园的饲养员给三群猴子分花生,如果只分给第一群猴子,则每只猴子可得12粒;如果只分给第二群猴子,则每只猴子可得15粒;如果只分给第三群猴子,则每只猴子可得20粒.那么花生同时分给三群猴子,平均每只猴子可得多少粒?
小试牛刀
练习:
一行小树苗,从第一棵到最后一棵的距离是90米,原来每隔2米一棵,由于小树长大了,要改为每隔5米一棵,如果两端不算,中间有几棵不必移动?
谢谢!
数的整除
知识要点
1.能被2整除的数的特征:
个位数字是0、2、4、6、8的整数.
2.能被5整除的数的特征:
个位数字是0或5的整数.
3.能被3(或9)整除的数的特征:
各个数字之和能被3(或9)整除.
4.能被4(或25)整除的数的特征:
末两位数能被4(或25)整除.
能被8(或125)整除的数的特征:
末三位数能被8(或125)整除.
知识要点
5.被11整除的数的特征是:
一个整数的奇数位上的数字之和与偶数位上的数字之和的差(大减小)是11的倍数.
6.能被7,11,
13整除的数的特征:
一个数的末三位与末三位以前的数字所组成的数的差能被7,11,
13整除。
典例精析
解:能被3整除的数的有
123
234
345
567
336
4392
64296
能被9整除的有
234
567
4392
64296
能被4整除的有336
4392
64296
例题1、下面各数中哪些能被3整除,哪些能被9整除,哪些能被4整除?
123
234
345
567
336
4392
64296
根据特征3
根据特征4
根据特征3
典例精析
解:能被4整除的数有
476
576
792
1288
3456
6676
170492
20228
能被7整除的数有476
1288
8638
170492
能被8整除的数有576
792
1288
3456
能被13整除的数有1599
20228
例题2、下面各数中哪些能被4整除,哪些能被7整除,哪些能被8整除?哪些能被13整除?
476
576
792
1288
3456
6676
8638
1599
170492
20228
根据特征3
根据特征6
根据特征4
根据特征6
典例精析
解:∵
173a能被9整除,
∴
1+7+3+a=11+a能被9整除,∴
a=7;
∵
173a能被11整除,
∴(7+a)-(3+1)=3+a能被11整除,∴a=8;
∵
173a能被6整除,
∴a是偶数且1+7+3+a=11+a能被3整除,
∴
a=4;
∴综上所述:数学老师先后所取的三个数字的和是
7+8+4=19.
例题3、
173a是一个四位数,数学老师说:“我们把a取三个不同的数,所得的三个四位数,依次可以被9、11、6整除”。
问:这先后所取的三个数字的和是多少?
典例精析
解:
∵27ab能被2、5整除,
∴可以判定b=0。
又∵27ab又能被4整除,
∴可能是00,20,40,60,80.
∵又27ab能被9和3整除,可以判定a=0.
∴
27ab=2700.
例题4、一个四位数27ab能同时被2,3,4,5,9整除,则这个四位数是多少?
典例精析
解:∵
1x2x3x4x5能被11整除,
∴(1+2+3+4+5)-4x=15-4x能被11整除或者4x-15
能被11整除;
又∵x是大于等于0,小于等于9的整数,
∴只有
x=1满足条件。
∴这个整数为112131415。
例题5、已知1x2x3x4x5整数能被11整除,求所有满足这个条件的整数。
典例精析
解:因为65=5×13,又因为5和13互素,
所以
既能被5整除又能被13整除。
能被5整除,可以得出y=0
或5;当
y=0时,x=7
;当y=5
时,x=9;所以满足条件的六位数是917930
和919935.
例题6、已知
能被65整除,求满足条件的六位数
特征2
特征6
特征6
典例精析
解法一:设这个三位数是
,根据题意可知这个六位数
.因为
=0,所以
能被7,11,13整除。即任意三位数连写一次得到的一个六位数能被7,11,13整除.
例题7、任意三位数连写一次得到的一个六位数是否能被7,11,13整除?
特征6
例题8:
某数被2除余1,被3除余2,被4除余3,被5除余4,满足以上条件的数有多少个?最小的一个数是几?
解:这个数,加上1,就能同时被
2,3,4,5整除
2,3,4,5的最小公倍数为60
满足要求的最小的数为:60-1=59
这样的数有无数多个
59再加上60的整数倍,都满足要求
例如:59+60=119
59+60
2=179
典例精析
典例精析
解:
∵(
1625,1170)=5×13
(方法一)∵AB:1625÷65=25,BC:1170÷65=18
∴25+18+1=44
∴这条街道最少要安装44盏路灯.
(方法二)∵AB:1625÷65=25,
BC:1170÷65=18
∴(25+1)+(18+1)-1=44
∴这条街道最少要安装44盏路灯.
(方法三)∵AB+BC:
(1625+1170)÷65=43
∴43+1=44
∴这条街道最少要安装44盏路灯.
例题9.如图,街道ABC在B处拐弯,在街道的一侧要等距离安装路灯,并要求在A、B、C处各安装一盏路灯,问这条街道最少要安装多少盏路灯?
小试牛刀
练习:
动物园的饲养员给三群猴子分花生,如果只分给第一群猴子,则每只猴子可得12粒;如果只分给第二群猴子,则每只猴子可得15粒;如果只分给第三群猴子,则每只猴子可得20粒.那么花生同时分给三群猴子,平均每只猴子可得多少粒?
小试牛刀
练习:
一行小树苗,从第一棵到最后一棵的距离是90米,原来每隔2米一棵,由于小树长大了,要改为每隔5米一棵,如果两端不算,中间有几棵不必移动?
谢谢!
