北师大版数学八年级上册2.3 立方根习题课件(24张)
文档属性
| 名称 | 北师大版数学八年级上册2.3 立方根习题课件(24张) |  | |
| 格式 | ppt | ||
| 文件大小 | 754.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-23 23:49:11 | ||
图片预览








文档简介
第二章 实数
3 立方根
名师导学
A. 一般地,如果一个数x的__________等于a,即__________=a,那么这个数x就叫做a的立方根.
求一个数a的立方根的运算,叫做__________.
立方
x3
开立方
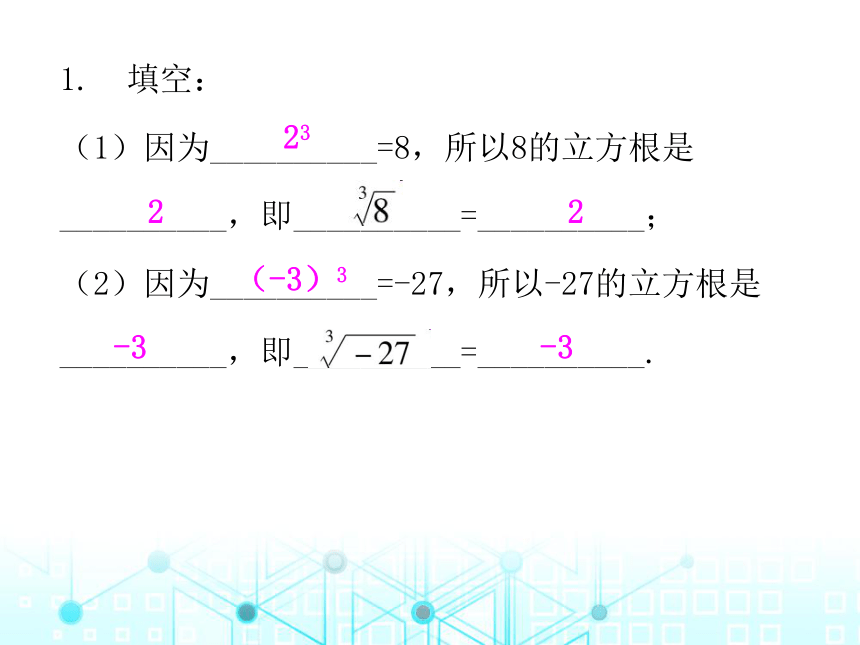
1. 填空:
(1)因为__________=8,所以8的立方根是__________,即__________=__________;
(2)因为__________=-27,所以-27的立方根是__________,即__________=__________.
23
2
2
(-3)3
-3
-3
B. 正数的立方根是__________,0的立方根是__________;负数的立方根是__________.
正数
0
负数
2. 125的立方根是__________,0的立方根是__________,-125的立方根是__________.
5
0
-5
课堂讲练
典型例题
新知1:立方根的概念
【例1】下列说法正确的是 ( )
A. 的立方根是2
B. -3是27的立方根
C. 的立方根是±
D. (-1)2的立方根是-1
A
模拟演练
1. 下列语句正确的是 ( )
A. 如果一个数的立方根是这个数本身,那么这个数一定是0
B. 一个数的立方根不是正数就是负数
C. 负数没有立方根
D. 一个不为零的数的立方根和这个数同号,0的立方根是0
D
新知2:开立方
【例2】求下列各数的立方根:
(1)27;
解:(1)因为33=27,所以27的立方根是3.
典型例题
(3)0.001.
(2)-64;
(2)因为(-4)3=-64,所以-64的立方根是-4.
(3)因为0.13=0.001,所以0.001的立方根
是0.1.
模拟演练
2. 求下列各数的立方根:
(1)343; (2)0.729; (3)
解:(1)因为73=343,所以343的立方根是7.
(2)因为0.93=0.729,所以0.729的立方根是0.9.
(3)因为
所以 的立方根是- .
【例3】求下列各式的值:
(1) ; (2) ;
解: =-2.
解: =0.4.
典型例题
解:( )3=9.
解:
模拟演练
3. 求下列各式的值:
(1) ;
解: =-1.
解:
解: =20.
解:
分层训练
【A组】
1. 关于立方根,下列说法正确的是 ( )
A. 正数有两个立方根
B. 立方根等于它本身的数只有0
C. 负数的立方根是负数
D. 负数没有立方根
C
2. 下列计算错误的是 ( )
A. =6 B. =-4
C. =-3 D. - =-0.1
C
3. 下列说法正确的有 ( )
①±2都是8的立方根;② =x;③ 的立方根是3;④- =2.
A. 1个 B. 2个 C. 3个 D. 4个
B
4. 的平方根是 ( )
A. 5
B.
C. ±
D. ±5
C
【B组】
5. 求下列各数的立方根:
(1)8; (2)-0.512; (3)±2 ; (4)
解:(1)因为23=8,所以8的立方根为2.
(2)因为(-0.8)3=-0.512,所以-0.512的立方根为-0.8.
(3)因为
所以±2 的立方根为± .
(4) =4,4的立方根为 ,所以 的立方根为 .
6. 求下列各式中x的值:
(1) x3=- ;(2) (x+1)3=27;
解:(1)x=- .
(2)因为(x+1)3=27,所以x+1=3. 所以x=2.
(3) x3-3= ; (4) =250.
解:(3)因为x3-3= ,所以x3= . 所以x= .
(4)因为 =250,所以 =125.
所以 x+1=5. 解得x=12.
【C组】
7. 已知某正数的两个平方根分别是2m-3和5-m,n-1的算术平方根为2,求3+m+n-7的立方根.
解:因为某正数的两个平方根分别是2m-3和5-m,
所以2m-3+5-m=0. 解得m=-2.
因为n-1的算术平方根为2,
所以n-1=4. 解得n=5.
所以3+m+n-7=-1.
所以3+m+n-7的立方根为-1.
8. 已知一个正方体的体积是1 000 cm3,现在要在它的8个角上分别截去8个大小相同的小正方体,使截去后余下的体积是488 cm3,问截得的每个小正方体的棱长是多少?
解:设截得的每个小正方体的棱长为x cm.
依题意,得1 000-8x3=488.
所以8x3=512.
解得x=4.
答:截得的每个小正方体的棱长是4 cm.
3 立方根
名师导学
A. 一般地,如果一个数x的__________等于a,即__________=a,那么这个数x就叫做a的立方根.
求一个数a的立方根的运算,叫做__________.
立方
x3
开立方
1. 填空:
(1)因为__________=8,所以8的立方根是__________,即__________=__________;
(2)因为__________=-27,所以-27的立方根是__________,即__________=__________.
23
2
2
(-3)3
-3
-3
B. 正数的立方根是__________,0的立方根是__________;负数的立方根是__________.
正数
0
负数
2. 125的立方根是__________,0的立方根是__________,-125的立方根是__________.
5
0
-5
课堂讲练
典型例题
新知1:立方根的概念
【例1】下列说法正确的是 ( )
A. 的立方根是2
B. -3是27的立方根
C. 的立方根是±
D. (-1)2的立方根是-1
A
模拟演练
1. 下列语句正确的是 ( )
A. 如果一个数的立方根是这个数本身,那么这个数一定是0
B. 一个数的立方根不是正数就是负数
C. 负数没有立方根
D. 一个不为零的数的立方根和这个数同号,0的立方根是0
D
新知2:开立方
【例2】求下列各数的立方根:
(1)27;
解:(1)因为33=27,所以27的立方根是3.
典型例题
(3)0.001.
(2)-64;
(2)因为(-4)3=-64,所以-64的立方根是-4.
(3)因为0.13=0.001,所以0.001的立方根
是0.1.
模拟演练
2. 求下列各数的立方根:
(1)343; (2)0.729; (3)
解:(1)因为73=343,所以343的立方根是7.
(2)因为0.93=0.729,所以0.729的立方根是0.9.
(3)因为
所以 的立方根是- .
【例3】求下列各式的值:
(1) ; (2) ;
解: =-2.
解: =0.4.
典型例题
解:( )3=9.
解:
模拟演练
3. 求下列各式的值:
(1) ;
解: =-1.
解:
解: =20.
解:
分层训练
【A组】
1. 关于立方根,下列说法正确的是 ( )
A. 正数有两个立方根
B. 立方根等于它本身的数只有0
C. 负数的立方根是负数
D. 负数没有立方根
C
2. 下列计算错误的是 ( )
A. =6 B. =-4
C. =-3 D. - =-0.1
C
3. 下列说法正确的有 ( )
①±2都是8的立方根;② =x;③ 的立方根是3;④- =2.
A. 1个 B. 2个 C. 3个 D. 4个
B
4. 的平方根是 ( )
A. 5
B.
C. ±
D. ±5
C
【B组】
5. 求下列各数的立方根:
(1)8; (2)-0.512; (3)±2 ; (4)
解:(1)因为23=8,所以8的立方根为2.
(2)因为(-0.8)3=-0.512,所以-0.512的立方根为-0.8.
(3)因为
所以±2 的立方根为± .
(4) =4,4的立方根为 ,所以 的立方根为 .
6. 求下列各式中x的值:
(1) x3=- ;(2) (x+1)3=27;
解:(1)x=- .
(2)因为(x+1)3=27,所以x+1=3. 所以x=2.
(3) x3-3= ; (4) =250.
解:(3)因为x3-3= ,所以x3= . 所以x= .
(4)因为 =250,所以 =125.
所以 x+1=5. 解得x=12.
【C组】
7. 已知某正数的两个平方根分别是2m-3和5-m,n-1的算术平方根为2,求3+m+n-7的立方根.
解:因为某正数的两个平方根分别是2m-3和5-m,
所以2m-3+5-m=0. 解得m=-2.
因为n-1的算术平方根为2,
所以n-1=4. 解得n=5.
所以3+m+n-7=-1.
所以3+m+n-7的立方根为-1.
8. 已知一个正方体的体积是1 000 cm3,现在要在它的8个角上分别截去8个大小相同的小正方体,使截去后余下的体积是488 cm3,问截得的每个小正方体的棱长是多少?
解:设截得的每个小正方体的棱长为x cm.
依题意,得1 000-8x3=488.
所以8x3=512.
解得x=4.
答:截得的每个小正方体的棱长是4 cm.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
