北师大版数学八年级上册2.4 估算习题课件(21张ppt)
文档属性
| 名称 | 北师大版数学八年级上册2.4 估算习题课件(21张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 785.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-24 00:00:00 | ||
图片预览








文档简介
第二章 实数
4 估 算
名师导学
A. 通过估算,可以求出无理数的近似值.
1. 估计7的值在( )
A. 0和1之间
B. 1和2之间
C. 2和3之间
D. 3和4之间
C
B. 通过估算,可以比较数的大小.
2. 比较大小:
__________2;
-5 _______-6 .
<
>
课堂讲练
典型例题
新知1:用估算的方法求无理数的近似值
【例1】下列实数中,在4和5之间的是 ( )A. π
B.
C.
D. 2π
B
模拟演练
1. 若m= -3,则m的范围是 ( )
A. 1<m<2 B. 2<m<3
C. 3<m<4 D. 4<m<5
B
【例2】估算 的大小.(误差小于0.1)
解:因为36<43<49,所以6< <7.
所以 的整数部分是6.
因为6.52=42.25,6.62=43.56,
所以6.5< <6.6.
所以 ≈6.5或 ≈6.6.
典型例题
模拟演练
2. 估算 的大小.(结果精确到1)
解:因为93=729,103=1 000,
9.13=753.571,9.23=778.688,9.33=804.357,9.43=830.584,9.53=857.375,9.63=884.736,9.73=912.673,
所以 ≈9.6≈10.
新知2:用估算的方法比较数的大小
【例3】比较 与0.5的大小.
解:因为
所以
所以
所以
典型例题
模拟演练
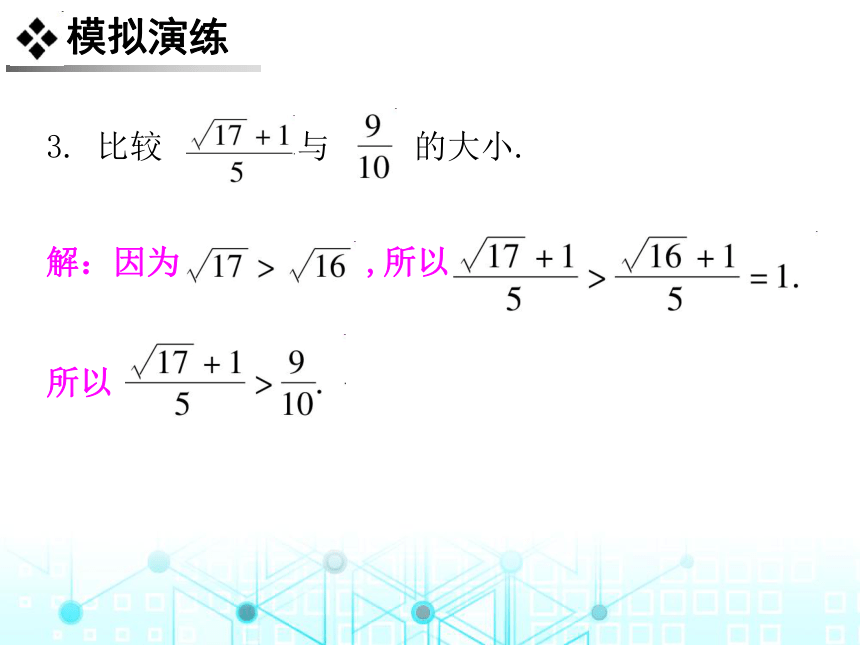
3. 比较 与 的大小.
解:因为 ,所以
所以
分层训练
【A组】
1. 下列整数中,与 最接近的是 ( )
A. 4 B. 5 C. 6 D. 7
2. 估计 的值约为 ( )
A. 2.73 B. 1.73 C. -1.73 D. -2.73
C
B
3. 通过估算,下列不等式不成立的是 ( )
A. >3.85 B. <4.02
C. <3.8 D. >2
B
4. 通过估算,估计 的大小应在 ( )
A. 7~8之间
B. 8.0~8.5之间
C. 8.5~9.0之间
D. 9~10之间
C
5. 比较2, 的大小,正确的是( )
A
6. 估算 的值是在 ( )
A. 2与3之间
B. 3与4之间
C. 4与5之间
D. 5与6之间
C
【B组】
7. 已知a=2- ,b= -2,c=5-2 ,那么a,b,c的大小顺序是 ( )
A. a<b<c
B. a<c<b
C. b<a<c
D. c<a<b
A
8. 根据下表回答下列问题:
x
28.1
28.1
28.2
28.3
28.4
28.5
28.6
28.7
x2
784.00
789.61
795.24
800.89
806.56
812.25
817.96
823.69
(1)795.24的平方根是__________,
≈__________;
(2)表中与 最接近的数是__________;
(3) 在数__________与__________之间.
±28.2
28.7
28.3
28.4
28.5
9. 通过估算,比较下列各组数的大小:
解:
解:
【C组】
10. 阅读理解:求 的近似值.
解:设 =10+x,其中0<x<1,
则103=(10+x)2,即103=100+20x+x2.
因为0<x<1,所以0<x2<1.
所以103≈100+20x.
解得x≈0.15,即 的近似值为10.15.
理解应用:利用上面的方法求 的近似值.(结果精确到0.01)
解:设 =10-x,其中0<x<1,
则95=(10-x)2,即95=100-20x+x2.
因为0<x<1,所以0<x2<1,
所以95≈100-20x.
解得x≈0.25,
即 的近似值为9.75.
11. 阅读下面的文字,然后解答问题.
因为22<7<32,所以2< <3.
所以 的整数部分为2,小数部分为 -2.
请解答:
(1) 的整数部分是__________,小数部分是__________;
(2)如果 的小数部分为a, 的整数部分为b,求a+b- 的值.
3
-3
解:(2)因为22<5<32,所以2< <3.
所以 的小数部分为a= -2.
因为62<37<72,所以6< <7.
所以 的整数部分为b=6.
所以a+b- = -2+6- =4.
4 估 算
名师导学
A. 通过估算,可以求出无理数的近似值.
1. 估计7的值在( )
A. 0和1之间
B. 1和2之间
C. 2和3之间
D. 3和4之间
C
B. 通过估算,可以比较数的大小.
2. 比较大小:
__________2;
-5 _______-6 .
<
>
课堂讲练
典型例题
新知1:用估算的方法求无理数的近似值
【例1】下列实数中,在4和5之间的是 ( )A. π
B.
C.
D. 2π
B
模拟演练
1. 若m= -3,则m的范围是 ( )
A. 1<m<2 B. 2<m<3
C. 3<m<4 D. 4<m<5
B
【例2】估算 的大小.(误差小于0.1)
解:因为36<43<49,所以6< <7.
所以 的整数部分是6.
因为6.52=42.25,6.62=43.56,
所以6.5< <6.6.
所以 ≈6.5或 ≈6.6.
典型例题
模拟演练
2. 估算 的大小.(结果精确到1)
解:因为93=729,103=1 000,
9.13=753.571,9.23=778.688,9.33=804.357,9.43=830.584,9.53=857.375,9.63=884.736,9.73=912.673,
所以 ≈9.6≈10.
新知2:用估算的方法比较数的大小
【例3】比较 与0.5的大小.
解:因为
所以
所以
所以
典型例题
模拟演练
3. 比较 与 的大小.
解:因为 ,所以
所以
分层训练
【A组】
1. 下列整数中,与 最接近的是 ( )
A. 4 B. 5 C. 6 D. 7
2. 估计 的值约为 ( )
A. 2.73 B. 1.73 C. -1.73 D. -2.73
C
B
3. 通过估算,下列不等式不成立的是 ( )
A. >3.85 B. <4.02
C. <3.8 D. >2
B
4. 通过估算,估计 的大小应在 ( )
A. 7~8之间
B. 8.0~8.5之间
C. 8.5~9.0之间
D. 9~10之间
C
5. 比较2, 的大小,正确的是( )
A
6. 估算 的值是在 ( )
A. 2与3之间
B. 3与4之间
C. 4与5之间
D. 5与6之间
C
【B组】
7. 已知a=2- ,b= -2,c=5-2 ,那么a,b,c的大小顺序是 ( )
A. a<b<c
B. a<c<b
C. b<a<c
D. c<a<b
A
8. 根据下表回答下列问题:
x
28.1
28.1
28.2
28.3
28.4
28.5
28.6
28.7
x2
784.00
789.61
795.24
800.89
806.56
812.25
817.96
823.69
(1)795.24的平方根是__________,
≈__________;
(2)表中与 最接近的数是__________;
(3) 在数__________与__________之间.
±28.2
28.7
28.3
28.4
28.5
9. 通过估算,比较下列各组数的大小:
解:
解:
【C组】
10. 阅读理解:求 的近似值.
解:设 =10+x,其中0<x<1,
则103=(10+x)2,即103=100+20x+x2.
因为0<x<1,所以0<x2<1.
所以103≈100+20x.
解得x≈0.15,即 的近似值为10.15.
理解应用:利用上面的方法求 的近似值.(结果精确到0.01)
解:设 =10-x,其中0<x<1,
则95=(10-x)2,即95=100-20x+x2.
因为0<x<1,所以0<x2<1,
所以95≈100-20x.
解得x≈0.25,
即 的近似值为9.75.
11. 阅读下面的文字,然后解答问题.
因为22<7<32,所以2< <3.
所以 的整数部分为2,小数部分为 -2.
请解答:
(1) 的整数部分是__________,小数部分是__________;
(2)如果 的小数部分为a, 的整数部分为b,求a+b- 的值.
3
-3
解:(2)因为22<5<32,所以2< <3.
所以 的小数部分为a= -2.
因为62<37<72,所以6< <7.
所以 的整数部分为b=6.
所以a+b- = -2+6- =4.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
