2019-2020学年山东省烟台市莱州市七年级下学期期末数学试卷(五四学制) (word版,含解析)
文档属性
| 名称 | 2019-2020学年山东省烟台市莱州市七年级下学期期末数学试卷(五四学制) (word版,含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 758.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-24 06:16:31 | ||
图片预览




文档简介
2019-2020学年山东省烟台市莱州市七年级第二学期期末数学试卷(五四学制)
一、选择题(共10小题).
1.下列语句中,不是命题的是( )
A.过一点作已知直线的垂线
B.两点确定一条直线
C.钝角大于90°
D.平角都相等
2.对于“莱州市明天的降雨概率是80%”这种说法,下列解释中正确的是( )
A.莱州市明天将有80%的地区降雨
B.莱州市明天将有80%的时间降雨
C.莱州市明天降雨的可能性比较大
D.莱州市明天肯定下雨
3.如图,在△ABC中,点D,E在边上,DE∥BC,若△ADE是等边三角形,AD=2,BD=3,则△ABC的周长为( )
A.6 B.9 C.15 D.18
4.关于x的不等式2x+a≤1只有2个正整数解,则a的取值范围为( )
A.﹣5<a<﹣3 B.﹣5≤a<﹣3 C.﹣5<a≤﹣3 D.﹣5≤a≤﹣3
5.如图,两条平行线a,b被直线c所截,若∠2=2∠1,则∠2等于( )
A.60° B.110° C.120° D.150°
6.若直线y=2x﹣3与直线y=5x+2的交点坐标为(a,b),则解为的方程组是( )
A. B.
C. D.
7.已知方程组,那么代数式8x﹣y﹣z的值是( )
A.6 B.7 C.8 D.9
8.以下列长度的三条线段为边,不能构成直角三角形的是( )
A.12cm,13cm,5cm B.6cm,8cm,10cm
C.4cm,5cm,6cm D.8cm,15cm,17cm
9.在如图所示的圆形图案中,黑白两色的直角三角形都全等.甲、乙两人将它作为一个游戏盘,游戏规则如下:按一定距离向盘中投镖一次(扎不中游戏盘重新投镖),扎在黑色区域为甲胜,扎在白色区域为乙胜,则这个游戏( )
A.对双方公平 B.对甲有利
C.对乙有利 D.无法确定公平性
10.如图,直线y=kx+3经过点(2,0),则关于x的不等式kx+3>0的解集是( )
A.x>2 B.x<2 C.x≥2 D.x≤2
二、填空题(本题共10个小题)
11.《论语十则》中有句话是“知之为知之,不知为不知.”在这句话中,“知”字出现的频率为 .
12.“四边形是多边形”的逆命题是 .
13.若<m<3,则点P(5m﹣2,m﹣3)在第 象限.
14.如图,△ABC为直角三角形,∠ACB=90°,CD⊥AB于点D,与∠1相等的角是 .
15.已知直线a∥b,将一个含有45°角的直角三角板(∠C=90°)按如图所示的位置摆放,若∠1=60°,则∠2的度数是 .
16.如图,在Rt△ABC中,∠C=90°,∠B=15°,DE垂直平分AB交BC于点E,BE=6,则AC= .
17.在△ABC中,AB=AC=13,BC=10,则BC边上的高为 .
18.已知:a、b是等腰三角形ABC的两边长,且满足(a﹣5)2+|b﹣6|=0,则△ABC的周长为 .
19.用反证法证明:在一个三角形中,如果两个角不相等,那么这两个角所对的边也不相等.证明时,可以先假设 .
20.若△ABC≌△DEF,△DEF的周长为12,AB=3,BC=4,则△ABC的面积为 .
三、解答题(本大题共9个小题)
21.(1)用加减消元法解方程组:;
(2)求不等式组的正整数解.
22.如图,直线l1,l2,l3表示三条相互交叉的公路,现在要建设一个货物中转站,要求它到三条公路的距离相等,请确定中转站P的位置.要求:用尺规作图,保留作图痕迹,标注字母P,不写作法.
23.一个不透明的袋中装有红、黄、白三种颜色球共100个,它们除颜色外都相同,其中黄球个数是白球个数的2倍少5个.已知从袋中摸出一个球是红球的概率是.
(1)求袋中红球的个数;
(2)求从袋中摸出一个球是白球的概率;
(3)取走10个球(其中没有红球)后,求从剩余的球中摸出一个球是红球的概率.
24.已知是方程组的解,求(m+2n)(m﹣2n)的值.
25.已知关于x的方程5x+2m=3x﹣1的根是非负数,求实数m的取值范围.
26.如图,在△ABC中,AB=AC,D为BC的中点,DE⊥AB,DF⊥AC,垂足分别为E、F,求证:DE=DF.
27.如图,△ABC≌△DBE,∠CBE=60°,∠DCB=30°.求证:DC2+BE2=AC2.
28.有甲、乙两种客车,2辆甲种客车与3辆乙种客车的总载客量为180人,1辆甲种客车与2辆乙种客车的总载客量为105人.
(1)请问1辆甲种客车与1辆乙种客车的载客量分别为多少人?
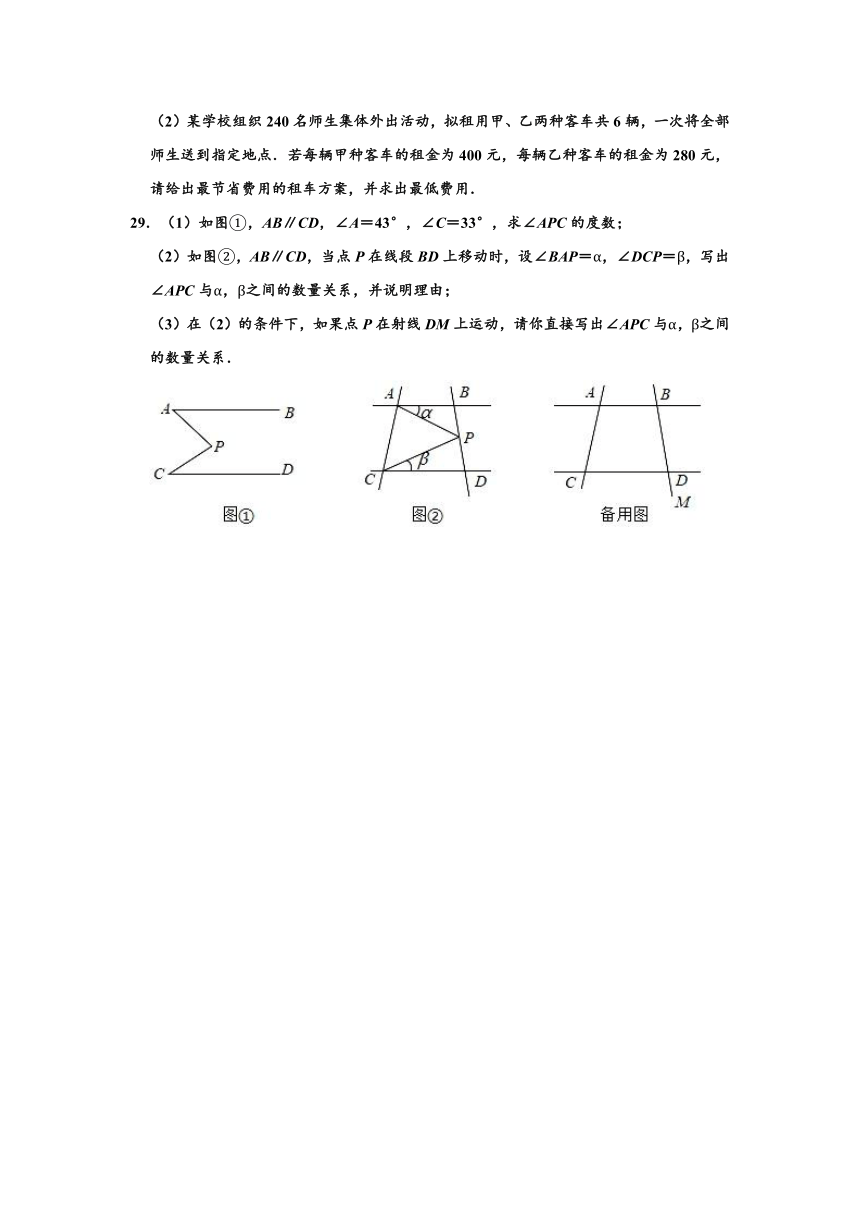
(2)某学校组织240名师生集体外出活动,拟租用甲、乙两种客车共6辆,一次将全部师生送到指定地点.若每辆甲种客车的租金为400元,每辆乙种客车的租金为280元,请给出最节省费用的租车方案,并求出最低费用.
29.(1)如图①,AB∥CD,∠A=43°,∠C=33°,求∠APC的度数;
(2)如图②,AB∥CD,当点P在线段BD上移动时,设∠BAP=α,∠DCP=β,写出∠APC与α,β之间的数量关系,并说明理由;
(3)在(2)的条件下,如果点P在射线DM上运动,请你直接写出∠APC与α,β之间的数量关系.
参考答案
一、选择题(共10小题).
1.下列语句中,不是命题的是( )
A.过一点作已知直线的垂线
B.两点确定一条直线
C.钝角大于90°
D.平角都相等
【分析】根据命题的定义:判断一件事情的语句叫命题,进行选择.
解:A、没判断一件事情,只是叙述一件事情,故不是命题;
B、两点确定一条直线,判断一件事情,故是命题;
C、钝角大于90°,判断一件事情,故是命题;
D、平角都相等,判断一件事情,故是命题;
故选:A.
2.对于“莱州市明天的降雨概率是80%”这种说法,下列解释中正确的是( )
A.莱州市明天将有80%的地区降雨
B.莱州市明天将有80%的时间降雨
C.莱州市明天降雨的可能性比较大
D.莱州市明天肯定下雨
【分析】概率值只是反映了事件发生的机会的大小,不是会一定发生.不确定事件就是随机事件,即可能发生也可能不发生的事件,发生的概率大于0并且小于1.
解:对于“莱州市明天的降雨概率是80%”,
可以解释为:莱州市明天降雨的可能性比较大.
故选:C.
3.如图,在△ABC中,点D,E在边上,DE∥BC,若△ADE是等边三角形,AD=2,BD=3,则△ABC的周长为( )
A.6 B.9 C.15 D.18
【分析】根据△ADE是等边三角形,可得∠ADE=∠AED=∠A=60°,根据DE∥BC,可得∠B=∠ADE=60°,∠C=∠AED=60°,所以△ABC是等边三角形,进而可求△ABC的周长.
解:∵△ADE是等边三角形,
∴∠ADE=∠AED=∠A=60°,
∵DE∥BC,
∴∠B=∠ADE=60°,∠C=∠AED=60°,
∴△ABC是等边三角形,
∴△ABC的周长为3AB=3×(2+3)=15.
故选:C.
4.关于x的不等式2x+a≤1只有2个正整数解,则a的取值范围为( )
A.﹣5<a<﹣3 B.﹣5≤a<﹣3 C.﹣5<a≤﹣3 D.﹣5≤a≤﹣3
【分析】首先解不等式求得不等式的解集,然后根据不等式只有两个正整数解即可得到一个关于a的不等式,求得a的值.
解:解不等式2x+a≤1得:x≤,
不等式有两个正整数解,一定是1和2,
根据题意得:2≤<3,
解得:﹣5<a≤﹣3.
故选:C.
5.如图,两条平行线a,b被直线c所截,若∠2=2∠1,则∠2等于( )
A.60° B.110° C.120° D.150°
【分析】根据两直线平行,同位角相等以及邻补角性质即可解答.
解:∵直线a∥b,
∴∠1=∠3,
∵∠2+∠3=180°,∠2=2∠1,
∴2∠1+∠1=180°,
∴∠1=60°,
即∠2=2∠1=120°.
故选:C.
6.若直线y=2x﹣3与直线y=5x+2的交点坐标为(a,b),则解为的方程组是( )
A. B.
C. D.
【分析】两条直线的交点坐标即为这两条直线的解析式组成的方程组的解.
解:∵直线y=2x﹣3与直线y=5x+2的交点坐标为(a,b),
∴解为的方程组是,即.
故选:C.
7.已知方程组,那么代数式8x﹣y﹣z的值是( )
A.6 B.7 C.8 D.9
【分析】根据“3x﹣y﹣2z=1”,得到﹣y﹣z=1+z﹣3x,代入8x﹣y﹣z得:5x+z+1,,①+②得:5x+z=6,代入5x+z+1,即可得到答案.
解:∵3x﹣y﹣2z=1,
∴﹣y﹣z=1+z﹣3x,
8x﹣y﹣z=1+z﹣3x+8x=5x+z+1,
,
①+②得:
5x+z=6,
即8x﹣y﹣z=6+1=7,
故选:B.
8.以下列长度的三条线段为边,不能构成直角三角形的是( )
A.12cm,13cm,5cm B.6cm,8cm,10cm
C.4cm,5cm,6cm D.8cm,15cm,17cm
【分析】先求出两小边的平方和,再求出最长边的平方,看看是否相等即可.
解:A、∵52+122=132,
∴以12cm、13cm、5cm为边组成的三角形是直角三角形,故本选项不符合题意;
B、∵62+82=102,
∴以6cm、8cm、10cm为边组成的三角形是直角三角形,故本选项不符合题意;
C、∵42+52≠62,
∴以4cm、5cm、6cm为边组成的三角形不是直角三角形,故本选项符合题意;
D、∵82+152=172,
∴以8cm、15cm、17cm为边组成的三角形是直角三角形,故本选项不符合题意;
故选:C.
9.在如图所示的圆形图案中,黑白两色的直角三角形都全等.甲、乙两人将它作为一个游戏盘,游戏规则如下:按一定距离向盘中投镖一次(扎不中游戏盘重新投镖),扎在黑色区域为甲胜,扎在白色区域为乙胜,则这个游戏( )
A.对双方公平 B.对甲有利
C.对乙有利 D.无法确定公平性
【分析】首先由图可得S黑色区域=S白色区域=S圆,然后由几何概率的知识,即可求得甲胜与乙胜的概率,比较概率的大小,即可求得答案.
解:由图知黑色区域的直角三角形有6个,弓形有3个,
白色区域的直角三角形有6个,弓形有3个,
所以甲获胜的概率等于乙获胜的概率,
所以这个游戏对双方公平,
故选:A.
10.如图,直线y=kx+3经过点(2,0),则关于x的不等式kx+3>0的解集是( )
A.x>2 B.x<2 C.x≥2 D.x≤2
【分析】先根据一次函数图象上点的坐标特征得到2k+3=0,解得k=﹣1.5,然后解不等式﹣1.5x+3>0即可.
解:∵直线y=kx+3经过点P(2,0)
∴2k+3=0,解得k=﹣1.5,
∴直线解析式为y=﹣1.5x+3,
解不等式﹣1.5x+3>0,得x<2,
即关于x的不等式kx+3>0的解集为x<2,
故选:B.
二、填空题(本题共10个小题)
11.《论语十则》中有句话是“知之为知之,不知为不知.”在这句话中,“知”字出现的频率为 .
【分析】用“知”字出现的次数除以字的总个数即可得.
解:∵这句话共有10个字,其中“知”字出现4次,
∴在这句话中,“知”字出现的频率为=,
故答案为:.
12.“四边形是多边形”的逆命题是 多边形是四边形 .
【分析】逆命题的概念就是把原来的题设和结论互换,因此可得到命题“四边形是多边形”的逆命题.
解:命题“四边形是多边形”的逆命题是“多边形是四边形”.
故答案为:多边形是四边形.
13.若<m<3,则点P(5m﹣2,m﹣3)在第 四 象限.
【分析】求出5m﹣2、m﹣3的正负情况,然后根据各象限内点的坐标特征解答.
解:∵<m<3,
∴5m﹣2>0,m﹣3<0,
∴点P在第四象限.
故答案为:四.
14.如图,△ABC为直角三角形,∠ACB=90°,CD⊥AB于点D,与∠1相等的角是 ∠B .
【分析】根据直角三角形的两锐角互余得到∠A+∠B=90°,∠A+∠1=90°,根据同角的余角相等解答.
解:∵∠ACB=90°,
∴∠A+∠B=90°,
∵CD⊥AB,
∴∠ADC=90°,
∴∠A+∠1=90°,
∴∠B=∠1,
故答案为:∠B.
15.已知直线a∥b,将一个含有45°角的直角三角板(∠C=90°)按如图所示的位置摆放,若∠1=60°,则∠2的度数是 75° .
【分析】由三角形外角的性质及对顶角相等可求出∠5的度数,由∠5的度数结合邻补角互补可求出∠3的度数,由直线a∥b得出∠2=∠3=75°,此题得解.
解:如图所示.
∵∠5=∠4+∠B,∠4=∠1=60°,∠B=45°,
∴∠5=45°+60°=105°.
∵∠3+∠5=180°,
∴∠3=75°.
∵直线a∥b,
∴∠2=∠3=75°,
故答案为:75°.
16.如图,在Rt△ABC中,∠C=90°,∠B=15°,DE垂直平分AB交BC于点E,BE=6,则AC= 3 .
【分析】①AE=BE=6;②∠AEC=2∠B=30°;③AE=2AC.
解:∵DE垂直平分AB,∴AE=BE=6,
∵∠B=15°,
∴∠AEC=∠B+∠BAE=30°.
∴AE=2AC.
故AC=3.
17.在△ABC中,AB=AC=13,BC=10,则BC边上的高为 12 .
【分析】过A作AD⊥BC于D,由等腰三角形的性质求出BD的长,根据勾股定理求出AD的长即可.
解:如图,等腰△ABC中,AB=AC=13,BC=10,
过A作AD⊥BC于D,则BD=5,
在Rt△ABD中,AB=13,BD=5,
则AD==12.
故BC边上高的长的高为12.
故答案是:12.
18.已知:a、b是等腰三角形ABC的两边长,且满足(a﹣5)2+|b﹣6|=0,则△ABC的周长为 16或17 .
【分析】根据非负数的意义列出关于a、b的方程并求出a、b的值,再根据a是腰长和底边长两种情况讨论求解.
解:∵(a﹣5)2+|b﹣6|=0,
∴a﹣5=0,b﹣6=0,
∴a=5,b=6,
(1)若5是腰长,则三角形的三边长为:5、5、6,
能组成三角形,周长为5+5+6=16;
(2)若5是底边长,则三角形的三边长为:5、6、6,
能组成三角形,
周长为5+6+6=17.
故答案为:16或17.
19.用反证法证明:在一个三角形中,如果两个角不相等,那么这两个角所对的边也不相等.证明时,可以先假设 这两个角所对的边相等 .
【分析】反证法的步骤中,第一步是假设结论不成立,反面成立,可据此进行判断.
解:反证法证明:在一个三角形中,如果两个角不相等,那么这两个角所对的边也不相等.
证明时,可以先假设这两个角所对的边相等,
故答案为:这两个角所对的边相等.
20.若△ABC≌△DEF,△DEF的周长为12,AB=3,BC=4,则△ABC的面积为 6 .
【分析】根据全等三角形的性质得到△ABC的周长为12,求出AC,根据勾股定理的逆定理得到△ABC为直角三角形,根据三角形的面积公式计算,得到答案.
解:∵△ABC≌△DEF,△DEF的周长为12,
∴△ABC的周长为12,
∴AC=12﹣AB﹣BC=12﹣3﹣4=5,
AC2=52=25,AB2+BC2=32+42=25,
∴AC2=AB2+BC2,
∴△ABC为直角三角形,
∴△ABC的面积=×AB×BC=×3×4=6,
故答案为:6.
三、解答题(本大题共9个小题)
21.(1)用加减消元法解方程组:;
(2)求不等式组的正整数解.
【分析】(1)方程组利用加减消元法求出解即可;
(2)分别求出不等式组中两不等式的解集,找出两解集的公共部分确定出不等式组的解集,进而求出正整数解即可.
解:(1),
①×2﹣②得:15x=30,
解得:x=2,
把x=2代入①得:y=1,
则方程组的解为;
(2),
由①得:x≥2,
由②得:x≤4,
∴原不等式组的解集为2≤x≤4,
则不等式组的正整数解为2,3,4.
22.如图,直线l1,l2,l3表示三条相互交叉的公路,现在要建设一个货物中转站,要求它到三条公路的距离相等,请确定中转站P的位置.要求:用尺规作图,保留作图痕迹,标注字母P,不写作法.
【分析】利用角平分线的性质定理解决问题即可,注意到三条公路的距离相等的点有四个.
解:如图,满足条件的点P有四个,如图所示:
23.一个不透明的袋中装有红、黄、白三种颜色球共100个,它们除颜色外都相同,其中黄球个数是白球个数的2倍少5个.已知从袋中摸出一个球是红球的概率是.
(1)求袋中红球的个数;
(2)求从袋中摸出一个球是白球的概率;
(3)取走10个球(其中没有红球)后,求从剩余的球中摸出一个球是红球的概率.
【分析】(1)根据红、黄、白三种颜色球共有的个数乘以红球的概率即可;
(2)设白球有x个,得出黄球有(2x﹣5)个,根据题意列出方程,求出白球的个数,再除以总的球数即可;
(3)先求出取走10个球后,还剩的球数,再根据红球的个数,除以还剩的球数即可.
解:(1)根据题意得:
100×,
答:红球有30个.
(2)设白球有x个,则黄球有(2x﹣5)个,
根据题意得x+2x﹣5=100﹣30
解得x=25.
所以摸出一个球是白球的概率P==;
(3)因为取走10个球后,还剩90个球,其中红球的个数没有变化,
所以从剩余的球中摸出一个球是红球的概率=;
24.已知是方程组的解,求(m+2n)(m﹣2n)的值.
【分析】将x=﹣1、y=2代入方程得到关于m、n的方程组,解之求出m、n的值,再代入代数式计算可得.
解:∵是方程组的解,
∴,
解得,
∴(m+2n)(m﹣2n)
=(6+2×2)(6﹣2×2)
=10×2
=20.
25.已知关于x的方程5x+2m=3x﹣1的根是非负数,求实数m的取值范围.
【分析】先求出方程的解,根据已知得出不等式,求出不等式的解集即可.
解:解方程5x+2m=3x﹣1得:x=﹣,
∵关于x的方程5x+2m=3x﹣1的根是非负数,
∴﹣≥0,
解得:m≤﹣,
即m 的取值范围是:m≤﹣.
26.如图,在△ABC中,AB=AC,D为BC的中点,DE⊥AB,DF⊥AC,垂足分别为E、F,求证:DE=DF.
【分析】根据等腰三角形的性质得出∠B=∠C,根据全等三角形的判定和性质得出DE=DF即可;
【解答】证明:∵AB=AC,
∴∠B=∠C,
又∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°,
∵点D为BC中点,
∴DB=DC,
∴在△DBE和△DCF中,
∴△DBE≌DCF(AAS),
∴DE=DF.
27.如图,△ABC≌△DBE,∠CBE=60°,∠DCB=30°.求证:DC2+BE2=AC2.
【分析】根据△ABC≌△BDE,得出AC=DE,BC=BE,连接CE,进一步得出△BCE为等边三角形;利用等边三角形的性质,进一步得出△DCE是直角三角形,问题得解.
【解答】证明:∵△ABC≌△DBE,
∴BE=BC,AC=ED;
连接EC.则△BCE为等边三角形,
∴BC=CE,∠BCE=60°,
∵∠DCB=30°,
∴∠DCE=90°,
在Rt△DCE中,
DC2+CE2=DE2,
∴DC2+BE2=AC2.
28.有甲、乙两种客车,2辆甲种客车与3辆乙种客车的总载客量为180人,1辆甲种客车与2辆乙种客车的总载客量为105人.
(1)请问1辆甲种客车与1辆乙种客车的载客量分别为多少人?
(2)某学校组织240名师生集体外出活动,拟租用甲、乙两种客车共6辆,一次将全部师生送到指定地点.若每辆甲种客车的租金为400元,每辆乙种客车的租金为280元,请给出最节省费用的租车方案,并求出最低费用.
【分析】(1)可设1辆甲种客车与1辆乙种客车的载客量分别为x人,y人,根据等量关系2辆甲种客车与3辆乙种客车的总载客量为180人,1辆甲种客车与2辆乙种客车的总载客量为105人,列出方程组求解即可;
(2)根据题意列出不等式组,进而求解即可.
解:(1)设1辆甲种客车与1辆乙种客车的载客量分别为x人,y人,
,
解得:,
答:1辆甲种客车与1辆乙种客车的载客量分别为45人和30人;
(2)设租用甲种客车a辆,依题意有:,
解得:6>a≥4,
因为a取整数,
所以a=4或5,
∵5×400+1×280>4×400+2×280,
∴a=4时,租车费用最低,为4×400+2×280=2160.
29.(1)如图①,AB∥CD,∠A=43°,∠C=33°,求∠APC的度数;
(2)如图②,AB∥CD,当点P在线段BD上移动时,设∠BAP=α,∠DCP=β,写出∠APC与α,β之间的数量关系,并说明理由;
(3)在(2)的条件下,如果点P在射线DM上运动,请你直接写出∠APC与α,β之间的数量关系.
【分析】(1)过P点作PE∥AB,由AB∥CD可得PE∥CD,利用平行线的性质可得∠APC=∠A+∠C,进而求解;
(2)过P点作PF∥AB,由AB∥CD可得PF∥CD,利用平行线的性质可得∠APC=α+β,即求解;
(3)过P点作PN∥AB,由AB∥CD可得PN∥CD,利用平行线的性质可得∠APC=α﹣β,即求解.
解:(1)过P点作PE∥AB,
∴∠APE=∠A,
∵AB∥CD,
∴PE∥CD,
∴∠EPC=∠C,
∵∠APC=∠APE+∠EPC,
∴∠APC=∠A+∠C
∵∠A=43°,∠C=33°,
∴∠APC=43°+33°=76°;
(2)∠APC=α+β.
理由:过P点作PF∥AB,
∴∠APF=∠BAP,
∵AB∥CD,
∴PF∥CD,
∴∠FPC=∠PCD,
∵∠APC=∠APF+∠FPC,
∴∠APC=∠BAP+∠PCD;
∵∠BAP=α,∠DCP=β,
∴∠APC=α+β;
(3)∠APC=α﹣β.
理由:过P点作PN∥AB,
∴∠APN=∠BAP,
∵AB∥CD,
∴PN∥CD,
∴∠NPC=∠PCD,
∵∠APC=∠APN﹣∠NPC,
∴∠APC=∠BAP﹣∠PCD;
∵∠BAP=α,∠DCP=β,
∴∠APC=α﹣β.
一、选择题(共10小题).
1.下列语句中,不是命题的是( )
A.过一点作已知直线的垂线
B.两点确定一条直线
C.钝角大于90°
D.平角都相等
2.对于“莱州市明天的降雨概率是80%”这种说法,下列解释中正确的是( )
A.莱州市明天将有80%的地区降雨
B.莱州市明天将有80%的时间降雨
C.莱州市明天降雨的可能性比较大
D.莱州市明天肯定下雨
3.如图,在△ABC中,点D,E在边上,DE∥BC,若△ADE是等边三角形,AD=2,BD=3,则△ABC的周长为( )
A.6 B.9 C.15 D.18
4.关于x的不等式2x+a≤1只有2个正整数解,则a的取值范围为( )
A.﹣5<a<﹣3 B.﹣5≤a<﹣3 C.﹣5<a≤﹣3 D.﹣5≤a≤﹣3
5.如图,两条平行线a,b被直线c所截,若∠2=2∠1,则∠2等于( )
A.60° B.110° C.120° D.150°
6.若直线y=2x﹣3与直线y=5x+2的交点坐标为(a,b),则解为的方程组是( )
A. B.
C. D.
7.已知方程组,那么代数式8x﹣y﹣z的值是( )
A.6 B.7 C.8 D.9
8.以下列长度的三条线段为边,不能构成直角三角形的是( )
A.12cm,13cm,5cm B.6cm,8cm,10cm
C.4cm,5cm,6cm D.8cm,15cm,17cm
9.在如图所示的圆形图案中,黑白两色的直角三角形都全等.甲、乙两人将它作为一个游戏盘,游戏规则如下:按一定距离向盘中投镖一次(扎不中游戏盘重新投镖),扎在黑色区域为甲胜,扎在白色区域为乙胜,则这个游戏( )
A.对双方公平 B.对甲有利
C.对乙有利 D.无法确定公平性
10.如图,直线y=kx+3经过点(2,0),则关于x的不等式kx+3>0的解集是( )
A.x>2 B.x<2 C.x≥2 D.x≤2
二、填空题(本题共10个小题)
11.《论语十则》中有句话是“知之为知之,不知为不知.”在这句话中,“知”字出现的频率为 .
12.“四边形是多边形”的逆命题是 .
13.若<m<3,则点P(5m﹣2,m﹣3)在第 象限.
14.如图,△ABC为直角三角形,∠ACB=90°,CD⊥AB于点D,与∠1相等的角是 .
15.已知直线a∥b,将一个含有45°角的直角三角板(∠C=90°)按如图所示的位置摆放,若∠1=60°,则∠2的度数是 .
16.如图,在Rt△ABC中,∠C=90°,∠B=15°,DE垂直平分AB交BC于点E,BE=6,则AC= .
17.在△ABC中,AB=AC=13,BC=10,则BC边上的高为 .
18.已知:a、b是等腰三角形ABC的两边长,且满足(a﹣5)2+|b﹣6|=0,则△ABC的周长为 .
19.用反证法证明:在一个三角形中,如果两个角不相等,那么这两个角所对的边也不相等.证明时,可以先假设 .
20.若△ABC≌△DEF,△DEF的周长为12,AB=3,BC=4,则△ABC的面积为 .
三、解答题(本大题共9个小题)
21.(1)用加减消元法解方程组:;
(2)求不等式组的正整数解.
22.如图,直线l1,l2,l3表示三条相互交叉的公路,现在要建设一个货物中转站,要求它到三条公路的距离相等,请确定中转站P的位置.要求:用尺规作图,保留作图痕迹,标注字母P,不写作法.
23.一个不透明的袋中装有红、黄、白三种颜色球共100个,它们除颜色外都相同,其中黄球个数是白球个数的2倍少5个.已知从袋中摸出一个球是红球的概率是.
(1)求袋中红球的个数;
(2)求从袋中摸出一个球是白球的概率;
(3)取走10个球(其中没有红球)后,求从剩余的球中摸出一个球是红球的概率.
24.已知是方程组的解,求(m+2n)(m﹣2n)的值.
25.已知关于x的方程5x+2m=3x﹣1的根是非负数,求实数m的取值范围.
26.如图,在△ABC中,AB=AC,D为BC的中点,DE⊥AB,DF⊥AC,垂足分别为E、F,求证:DE=DF.
27.如图,△ABC≌△DBE,∠CBE=60°,∠DCB=30°.求证:DC2+BE2=AC2.
28.有甲、乙两种客车,2辆甲种客车与3辆乙种客车的总载客量为180人,1辆甲种客车与2辆乙种客车的总载客量为105人.
(1)请问1辆甲种客车与1辆乙种客车的载客量分别为多少人?
(2)某学校组织240名师生集体外出活动,拟租用甲、乙两种客车共6辆,一次将全部师生送到指定地点.若每辆甲种客车的租金为400元,每辆乙种客车的租金为280元,请给出最节省费用的租车方案,并求出最低费用.
29.(1)如图①,AB∥CD,∠A=43°,∠C=33°,求∠APC的度数;
(2)如图②,AB∥CD,当点P在线段BD上移动时,设∠BAP=α,∠DCP=β,写出∠APC与α,β之间的数量关系,并说明理由;
(3)在(2)的条件下,如果点P在射线DM上运动,请你直接写出∠APC与α,β之间的数量关系.
参考答案
一、选择题(共10小题).
1.下列语句中,不是命题的是( )
A.过一点作已知直线的垂线
B.两点确定一条直线
C.钝角大于90°
D.平角都相等
【分析】根据命题的定义:判断一件事情的语句叫命题,进行选择.
解:A、没判断一件事情,只是叙述一件事情,故不是命题;
B、两点确定一条直线,判断一件事情,故是命题;
C、钝角大于90°,判断一件事情,故是命题;
D、平角都相等,判断一件事情,故是命题;
故选:A.
2.对于“莱州市明天的降雨概率是80%”这种说法,下列解释中正确的是( )
A.莱州市明天将有80%的地区降雨
B.莱州市明天将有80%的时间降雨
C.莱州市明天降雨的可能性比较大
D.莱州市明天肯定下雨
【分析】概率值只是反映了事件发生的机会的大小,不是会一定发生.不确定事件就是随机事件,即可能发生也可能不发生的事件,发生的概率大于0并且小于1.
解:对于“莱州市明天的降雨概率是80%”,
可以解释为:莱州市明天降雨的可能性比较大.
故选:C.
3.如图,在△ABC中,点D,E在边上,DE∥BC,若△ADE是等边三角形,AD=2,BD=3,则△ABC的周长为( )
A.6 B.9 C.15 D.18
【分析】根据△ADE是等边三角形,可得∠ADE=∠AED=∠A=60°,根据DE∥BC,可得∠B=∠ADE=60°,∠C=∠AED=60°,所以△ABC是等边三角形,进而可求△ABC的周长.
解:∵△ADE是等边三角形,
∴∠ADE=∠AED=∠A=60°,
∵DE∥BC,
∴∠B=∠ADE=60°,∠C=∠AED=60°,
∴△ABC是等边三角形,
∴△ABC的周长为3AB=3×(2+3)=15.
故选:C.
4.关于x的不等式2x+a≤1只有2个正整数解,则a的取值范围为( )
A.﹣5<a<﹣3 B.﹣5≤a<﹣3 C.﹣5<a≤﹣3 D.﹣5≤a≤﹣3
【分析】首先解不等式求得不等式的解集,然后根据不等式只有两个正整数解即可得到一个关于a的不等式,求得a的值.
解:解不等式2x+a≤1得:x≤,
不等式有两个正整数解,一定是1和2,
根据题意得:2≤<3,
解得:﹣5<a≤﹣3.
故选:C.
5.如图,两条平行线a,b被直线c所截,若∠2=2∠1,则∠2等于( )
A.60° B.110° C.120° D.150°
【分析】根据两直线平行,同位角相等以及邻补角性质即可解答.
解:∵直线a∥b,
∴∠1=∠3,
∵∠2+∠3=180°,∠2=2∠1,
∴2∠1+∠1=180°,
∴∠1=60°,
即∠2=2∠1=120°.
故选:C.
6.若直线y=2x﹣3与直线y=5x+2的交点坐标为(a,b),则解为的方程组是( )
A. B.
C. D.
【分析】两条直线的交点坐标即为这两条直线的解析式组成的方程组的解.
解:∵直线y=2x﹣3与直线y=5x+2的交点坐标为(a,b),
∴解为的方程组是,即.
故选:C.
7.已知方程组,那么代数式8x﹣y﹣z的值是( )
A.6 B.7 C.8 D.9
【分析】根据“3x﹣y﹣2z=1”,得到﹣y﹣z=1+z﹣3x,代入8x﹣y﹣z得:5x+z+1,,①+②得:5x+z=6,代入5x+z+1,即可得到答案.
解:∵3x﹣y﹣2z=1,
∴﹣y﹣z=1+z﹣3x,
8x﹣y﹣z=1+z﹣3x+8x=5x+z+1,
,
①+②得:
5x+z=6,
即8x﹣y﹣z=6+1=7,
故选:B.
8.以下列长度的三条线段为边,不能构成直角三角形的是( )
A.12cm,13cm,5cm B.6cm,8cm,10cm
C.4cm,5cm,6cm D.8cm,15cm,17cm
【分析】先求出两小边的平方和,再求出最长边的平方,看看是否相等即可.
解:A、∵52+122=132,
∴以12cm、13cm、5cm为边组成的三角形是直角三角形,故本选项不符合题意;
B、∵62+82=102,
∴以6cm、8cm、10cm为边组成的三角形是直角三角形,故本选项不符合题意;
C、∵42+52≠62,
∴以4cm、5cm、6cm为边组成的三角形不是直角三角形,故本选项符合题意;
D、∵82+152=172,
∴以8cm、15cm、17cm为边组成的三角形是直角三角形,故本选项不符合题意;
故选:C.
9.在如图所示的圆形图案中,黑白两色的直角三角形都全等.甲、乙两人将它作为一个游戏盘,游戏规则如下:按一定距离向盘中投镖一次(扎不中游戏盘重新投镖),扎在黑色区域为甲胜,扎在白色区域为乙胜,则这个游戏( )
A.对双方公平 B.对甲有利
C.对乙有利 D.无法确定公平性
【分析】首先由图可得S黑色区域=S白色区域=S圆,然后由几何概率的知识,即可求得甲胜与乙胜的概率,比较概率的大小,即可求得答案.
解:由图知黑色区域的直角三角形有6个,弓形有3个,
白色区域的直角三角形有6个,弓形有3个,
所以甲获胜的概率等于乙获胜的概率,
所以这个游戏对双方公平,
故选:A.
10.如图,直线y=kx+3经过点(2,0),则关于x的不等式kx+3>0的解集是( )
A.x>2 B.x<2 C.x≥2 D.x≤2
【分析】先根据一次函数图象上点的坐标特征得到2k+3=0,解得k=﹣1.5,然后解不等式﹣1.5x+3>0即可.
解:∵直线y=kx+3经过点P(2,0)
∴2k+3=0,解得k=﹣1.5,
∴直线解析式为y=﹣1.5x+3,
解不等式﹣1.5x+3>0,得x<2,
即关于x的不等式kx+3>0的解集为x<2,
故选:B.
二、填空题(本题共10个小题)
11.《论语十则》中有句话是“知之为知之,不知为不知.”在这句话中,“知”字出现的频率为 .
【分析】用“知”字出现的次数除以字的总个数即可得.
解:∵这句话共有10个字,其中“知”字出现4次,
∴在这句话中,“知”字出现的频率为=,
故答案为:.
12.“四边形是多边形”的逆命题是 多边形是四边形 .
【分析】逆命题的概念就是把原来的题设和结论互换,因此可得到命题“四边形是多边形”的逆命题.
解:命题“四边形是多边形”的逆命题是“多边形是四边形”.
故答案为:多边形是四边形.
13.若<m<3,则点P(5m﹣2,m﹣3)在第 四 象限.
【分析】求出5m﹣2、m﹣3的正负情况,然后根据各象限内点的坐标特征解答.
解:∵<m<3,
∴5m﹣2>0,m﹣3<0,
∴点P在第四象限.
故答案为:四.
14.如图,△ABC为直角三角形,∠ACB=90°,CD⊥AB于点D,与∠1相等的角是 ∠B .
【分析】根据直角三角形的两锐角互余得到∠A+∠B=90°,∠A+∠1=90°,根据同角的余角相等解答.
解:∵∠ACB=90°,
∴∠A+∠B=90°,
∵CD⊥AB,
∴∠ADC=90°,
∴∠A+∠1=90°,
∴∠B=∠1,
故答案为:∠B.
15.已知直线a∥b,将一个含有45°角的直角三角板(∠C=90°)按如图所示的位置摆放,若∠1=60°,则∠2的度数是 75° .
【分析】由三角形外角的性质及对顶角相等可求出∠5的度数,由∠5的度数结合邻补角互补可求出∠3的度数,由直线a∥b得出∠2=∠3=75°,此题得解.
解:如图所示.
∵∠5=∠4+∠B,∠4=∠1=60°,∠B=45°,
∴∠5=45°+60°=105°.
∵∠3+∠5=180°,
∴∠3=75°.
∵直线a∥b,
∴∠2=∠3=75°,
故答案为:75°.
16.如图,在Rt△ABC中,∠C=90°,∠B=15°,DE垂直平分AB交BC于点E,BE=6,则AC= 3 .
【分析】①AE=BE=6;②∠AEC=2∠B=30°;③AE=2AC.
解:∵DE垂直平分AB,∴AE=BE=6,
∵∠B=15°,
∴∠AEC=∠B+∠BAE=30°.
∴AE=2AC.
故AC=3.
17.在△ABC中,AB=AC=13,BC=10,则BC边上的高为 12 .
【分析】过A作AD⊥BC于D,由等腰三角形的性质求出BD的长,根据勾股定理求出AD的长即可.
解:如图,等腰△ABC中,AB=AC=13,BC=10,
过A作AD⊥BC于D,则BD=5,
在Rt△ABD中,AB=13,BD=5,
则AD==12.
故BC边上高的长的高为12.
故答案是:12.
18.已知:a、b是等腰三角形ABC的两边长,且满足(a﹣5)2+|b﹣6|=0,则△ABC的周长为 16或17 .
【分析】根据非负数的意义列出关于a、b的方程并求出a、b的值,再根据a是腰长和底边长两种情况讨论求解.
解:∵(a﹣5)2+|b﹣6|=0,
∴a﹣5=0,b﹣6=0,
∴a=5,b=6,
(1)若5是腰长,则三角形的三边长为:5、5、6,
能组成三角形,周长为5+5+6=16;
(2)若5是底边长,则三角形的三边长为:5、6、6,
能组成三角形,
周长为5+6+6=17.
故答案为:16或17.
19.用反证法证明:在一个三角形中,如果两个角不相等,那么这两个角所对的边也不相等.证明时,可以先假设 这两个角所对的边相等 .
【分析】反证法的步骤中,第一步是假设结论不成立,反面成立,可据此进行判断.
解:反证法证明:在一个三角形中,如果两个角不相等,那么这两个角所对的边也不相等.
证明时,可以先假设这两个角所对的边相等,
故答案为:这两个角所对的边相等.
20.若△ABC≌△DEF,△DEF的周长为12,AB=3,BC=4,则△ABC的面积为 6 .
【分析】根据全等三角形的性质得到△ABC的周长为12,求出AC,根据勾股定理的逆定理得到△ABC为直角三角形,根据三角形的面积公式计算,得到答案.
解:∵△ABC≌△DEF,△DEF的周长为12,
∴△ABC的周长为12,
∴AC=12﹣AB﹣BC=12﹣3﹣4=5,
AC2=52=25,AB2+BC2=32+42=25,
∴AC2=AB2+BC2,
∴△ABC为直角三角形,
∴△ABC的面积=×AB×BC=×3×4=6,
故答案为:6.
三、解答题(本大题共9个小题)
21.(1)用加减消元法解方程组:;
(2)求不等式组的正整数解.
【分析】(1)方程组利用加减消元法求出解即可;
(2)分别求出不等式组中两不等式的解集,找出两解集的公共部分确定出不等式组的解集,进而求出正整数解即可.
解:(1),
①×2﹣②得:15x=30,
解得:x=2,
把x=2代入①得:y=1,
则方程组的解为;
(2),
由①得:x≥2,
由②得:x≤4,
∴原不等式组的解集为2≤x≤4,
则不等式组的正整数解为2,3,4.
22.如图,直线l1,l2,l3表示三条相互交叉的公路,现在要建设一个货物中转站,要求它到三条公路的距离相等,请确定中转站P的位置.要求:用尺规作图,保留作图痕迹,标注字母P,不写作法.
【分析】利用角平分线的性质定理解决问题即可,注意到三条公路的距离相等的点有四个.
解:如图,满足条件的点P有四个,如图所示:
23.一个不透明的袋中装有红、黄、白三种颜色球共100个,它们除颜色外都相同,其中黄球个数是白球个数的2倍少5个.已知从袋中摸出一个球是红球的概率是.
(1)求袋中红球的个数;
(2)求从袋中摸出一个球是白球的概率;
(3)取走10个球(其中没有红球)后,求从剩余的球中摸出一个球是红球的概率.
【分析】(1)根据红、黄、白三种颜色球共有的个数乘以红球的概率即可;
(2)设白球有x个,得出黄球有(2x﹣5)个,根据题意列出方程,求出白球的个数,再除以总的球数即可;
(3)先求出取走10个球后,还剩的球数,再根据红球的个数,除以还剩的球数即可.
解:(1)根据题意得:
100×,
答:红球有30个.
(2)设白球有x个,则黄球有(2x﹣5)个,
根据题意得x+2x﹣5=100﹣30
解得x=25.
所以摸出一个球是白球的概率P==;
(3)因为取走10个球后,还剩90个球,其中红球的个数没有变化,
所以从剩余的球中摸出一个球是红球的概率=;
24.已知是方程组的解,求(m+2n)(m﹣2n)的值.
【分析】将x=﹣1、y=2代入方程得到关于m、n的方程组,解之求出m、n的值,再代入代数式计算可得.
解:∵是方程组的解,
∴,
解得,
∴(m+2n)(m﹣2n)
=(6+2×2)(6﹣2×2)
=10×2
=20.
25.已知关于x的方程5x+2m=3x﹣1的根是非负数,求实数m的取值范围.
【分析】先求出方程的解,根据已知得出不等式,求出不等式的解集即可.
解:解方程5x+2m=3x﹣1得:x=﹣,
∵关于x的方程5x+2m=3x﹣1的根是非负数,
∴﹣≥0,
解得:m≤﹣,
即m 的取值范围是:m≤﹣.
26.如图,在△ABC中,AB=AC,D为BC的中点,DE⊥AB,DF⊥AC,垂足分别为E、F,求证:DE=DF.
【分析】根据等腰三角形的性质得出∠B=∠C,根据全等三角形的判定和性质得出DE=DF即可;
【解答】证明:∵AB=AC,
∴∠B=∠C,
又∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°,
∵点D为BC中点,
∴DB=DC,
∴在△DBE和△DCF中,
∴△DBE≌DCF(AAS),
∴DE=DF.
27.如图,△ABC≌△DBE,∠CBE=60°,∠DCB=30°.求证:DC2+BE2=AC2.
【分析】根据△ABC≌△BDE,得出AC=DE,BC=BE,连接CE,进一步得出△BCE为等边三角形;利用等边三角形的性质,进一步得出△DCE是直角三角形,问题得解.
【解答】证明:∵△ABC≌△DBE,
∴BE=BC,AC=ED;
连接EC.则△BCE为等边三角形,
∴BC=CE,∠BCE=60°,
∵∠DCB=30°,
∴∠DCE=90°,
在Rt△DCE中,
DC2+CE2=DE2,
∴DC2+BE2=AC2.
28.有甲、乙两种客车,2辆甲种客车与3辆乙种客车的总载客量为180人,1辆甲种客车与2辆乙种客车的总载客量为105人.
(1)请问1辆甲种客车与1辆乙种客车的载客量分别为多少人?
(2)某学校组织240名师生集体外出活动,拟租用甲、乙两种客车共6辆,一次将全部师生送到指定地点.若每辆甲种客车的租金为400元,每辆乙种客车的租金为280元,请给出最节省费用的租车方案,并求出最低费用.
【分析】(1)可设1辆甲种客车与1辆乙种客车的载客量分别为x人,y人,根据等量关系2辆甲种客车与3辆乙种客车的总载客量为180人,1辆甲种客车与2辆乙种客车的总载客量为105人,列出方程组求解即可;
(2)根据题意列出不等式组,进而求解即可.
解:(1)设1辆甲种客车与1辆乙种客车的载客量分别为x人,y人,
,
解得:,
答:1辆甲种客车与1辆乙种客车的载客量分别为45人和30人;
(2)设租用甲种客车a辆,依题意有:,
解得:6>a≥4,
因为a取整数,
所以a=4或5,
∵5×400+1×280>4×400+2×280,
∴a=4时,租车费用最低,为4×400+2×280=2160.
29.(1)如图①,AB∥CD,∠A=43°,∠C=33°,求∠APC的度数;
(2)如图②,AB∥CD,当点P在线段BD上移动时,设∠BAP=α,∠DCP=β,写出∠APC与α,β之间的数量关系,并说明理由;
(3)在(2)的条件下,如果点P在射线DM上运动,请你直接写出∠APC与α,β之间的数量关系.
【分析】(1)过P点作PE∥AB,由AB∥CD可得PE∥CD,利用平行线的性质可得∠APC=∠A+∠C,进而求解;
(2)过P点作PF∥AB,由AB∥CD可得PF∥CD,利用平行线的性质可得∠APC=α+β,即求解;
(3)过P点作PN∥AB,由AB∥CD可得PN∥CD,利用平行线的性质可得∠APC=α﹣β,即求解.
解:(1)过P点作PE∥AB,
∴∠APE=∠A,
∵AB∥CD,
∴PE∥CD,
∴∠EPC=∠C,
∵∠APC=∠APE+∠EPC,
∴∠APC=∠A+∠C
∵∠A=43°,∠C=33°,
∴∠APC=43°+33°=76°;
(2)∠APC=α+β.
理由:过P点作PF∥AB,
∴∠APF=∠BAP,
∵AB∥CD,
∴PF∥CD,
∴∠FPC=∠PCD,
∵∠APC=∠APF+∠FPC,
∴∠APC=∠BAP+∠PCD;
∵∠BAP=α,∠DCP=β,
∴∠APC=α+β;
(3)∠APC=α﹣β.
理由:过P点作PN∥AB,
∴∠APN=∠BAP,
∵AB∥CD,
∴PN∥CD,
∴∠NPC=∠PCD,
∵∠APC=∠APN﹣∠NPC,
∴∠APC=∠BAP﹣∠PCD;
∵∠BAP=α,∠DCP=β,
∴∠APC=α﹣β.
同课章节目录
