六年级上册数学课件-5.1 圆的面积 解决问题青岛版 (共26张PPT)
文档属性
| 名称 | 六年级上册数学课件-5.1 圆的面积 解决问题青岛版 (共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 10.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-24 07:36:21 | ||
图片预览







文档简介
(共26张PPT)
妙用认知冲突
巧促深度思考
小学数学六年级上册第五单元《圆》的例3
一
二
三
四
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
圆的面积
解决问题
小学数学六年级上册第五单元《圆》的例3
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
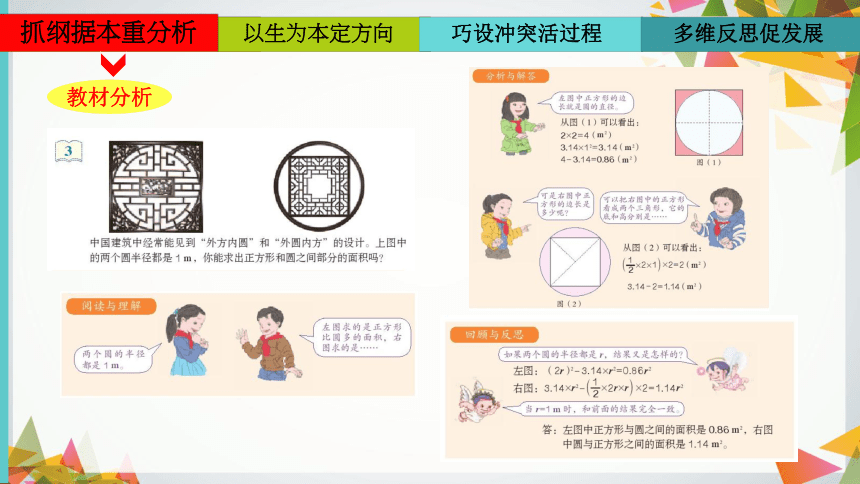
教材分析
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
教材分析
合作学习解决问题的意识
对不规则组合图形面积的思考经验
合作学习的有效方法
有序思考的方法
对正方形与圆形面积的教学计算经验
动手尝试的意愿
对一般结论定性分析的深度思考
对图形特殊数据定量计算的初步思考
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
学情分析
有
缺乏
3
2
1
结合具体情境认识与圆相关的组合图形的特征,掌握计算此类图形面积的方法,并能准确计算。
在解决实际问题的过程中,通过独立思考、合作探究、讨论交流等活动,培养学生分析问题和解决问题的能力,积累一般性的问题解决经验。
结合例题的教学,适时渗透中国传统文化的教育,通过体验数学与生活之间的联系感受数学的应用价值,培养学生的数学素养。
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
教学目标
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
教学重难点
使学生在解决求组合图形面积的过程中,积累一般性的问题解决经验。
重点
对解决组合图形的问题进行分析,培养学生的合作交流意识、发展学生数学思维能力。
难点
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
教学策略
重思想渗透,把实际问题转化为数学问题;
重几何直观,
寓实践于活动之中;
重拓展应用,寓特殊规律于一般方法延伸之中。
重知识内化,寓思考于讨论、探究之
中;
1
2
3
4
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
激活经验,引发冲突
外方内圆
外方内圆
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
合作共研,探究策略
巧设活动,制造认知冲突,启发学生思考。
1
外方内圆
外圆内方
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
合作共研,探究策略
巧设活动,制造认知冲突,启发学生思考。
1
外方内圆
外方内圆
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
合作共研,探究策略
巧设活动,制造认知冲突,启发学生思考。
1
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
合作共研,探究策略
诱发争辩,呈现认知冲突,激发学生思考。
2
两个圆的半径都是1
m。
怎样求正方形和圆
之间部分的面积?
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
合作共研,探究策略
诱发争辩,呈现认知冲突,激发学生思考。
2
正方形的边长就是圆的直径。
1m
2m
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
合作共研,探究策略
诱发争辩,呈现认知冲突,激发学生思考。
2
图中正方形的边长是多少呢?
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
合作共研,探究策略
诱发争辩,呈现认知冲突,激发学生思考。
2
图中正方形的边长是多少呢?
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
合作共研,探究策略
适时延伸,挖掘认知冲突,拓展学生思维。
3
那么我们解答得对不对呢?有什么方法验证吗?
如果两个圆的半径都是r,结果又是怎样的?
r
r
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
合作共研,探究策略
适时延伸,挖掘认知冲突,拓展学生思维。
3
r
如果圆的半径是r,结果又是怎样的?
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
合作共研,探究策略
适时延伸,挖掘认知冲突,拓展学生思维。
3
r
如果圆的半径是r,结果又是怎样的?
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
课堂练习,内化应用
基础练习。
1
右图是一面我国唐代外圆内方的铜镜。铜镜的直径是24
cm。外面的圆与内部的正方形之间的面积是多少?
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
课堂练习,内化应用
拓展练习。
2
右图两个正方形的边长都是2分米,比一比两个正方形中
阴影部分的面积。
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
全课总结,畅谈收获
说一说:这节课你有什么收获和体会?
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
板书设计
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
多元化评价
关注学生学习结果
让学生树立自信心
更关注情感与态度
体验学习数学的乐趣
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
总结与反思
小学数学六年级上册第五单元《圆》的例3
谢谢聆听
,
敬请指导!
妙用认知冲突
巧促深度思考
小学数学六年级上册第五单元《圆》的例3
一
二
三
四
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
圆的面积
解决问题
小学数学六年级上册第五单元《圆》的例3
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
教材分析
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
教材分析
合作学习解决问题的意识
对不规则组合图形面积的思考经验
合作学习的有效方法
有序思考的方法
对正方形与圆形面积的教学计算经验
动手尝试的意愿
对一般结论定性分析的深度思考
对图形特殊数据定量计算的初步思考
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
学情分析
有
缺乏
3
2
1
结合具体情境认识与圆相关的组合图形的特征,掌握计算此类图形面积的方法,并能准确计算。
在解决实际问题的过程中,通过独立思考、合作探究、讨论交流等活动,培养学生分析问题和解决问题的能力,积累一般性的问题解决经验。
结合例题的教学,适时渗透中国传统文化的教育,通过体验数学与生活之间的联系感受数学的应用价值,培养学生的数学素养。
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
教学目标
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
教学重难点
使学生在解决求组合图形面积的过程中,积累一般性的问题解决经验。
重点
对解决组合图形的问题进行分析,培养学生的合作交流意识、发展学生数学思维能力。
难点
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
教学策略
重思想渗透,把实际问题转化为数学问题;
重几何直观,
寓实践于活动之中;
重拓展应用,寓特殊规律于一般方法延伸之中。
重知识内化,寓思考于讨论、探究之
中;
1
2
3
4
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
激活经验,引发冲突
外方内圆
外方内圆
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
合作共研,探究策略
巧设活动,制造认知冲突,启发学生思考。
1
外方内圆
外圆内方
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
合作共研,探究策略
巧设活动,制造认知冲突,启发学生思考。
1
外方内圆
外方内圆
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
合作共研,探究策略
巧设活动,制造认知冲突,启发学生思考。
1
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
合作共研,探究策略
诱发争辩,呈现认知冲突,激发学生思考。
2
两个圆的半径都是1
m。
怎样求正方形和圆
之间部分的面积?
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
合作共研,探究策略
诱发争辩,呈现认知冲突,激发学生思考。
2
正方形的边长就是圆的直径。
1m
2m
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
合作共研,探究策略
诱发争辩,呈现认知冲突,激发学生思考。
2
图中正方形的边长是多少呢?
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
合作共研,探究策略
诱发争辩,呈现认知冲突,激发学生思考。
2
图中正方形的边长是多少呢?
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
合作共研,探究策略
适时延伸,挖掘认知冲突,拓展学生思维。
3
那么我们解答得对不对呢?有什么方法验证吗?
如果两个圆的半径都是r,结果又是怎样的?
r
r
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
合作共研,探究策略
适时延伸,挖掘认知冲突,拓展学生思维。
3
r
如果圆的半径是r,结果又是怎样的?
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
合作共研,探究策略
适时延伸,挖掘认知冲突,拓展学生思维。
3
r
如果圆的半径是r,结果又是怎样的?
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
课堂练习,内化应用
基础练习。
1
右图是一面我国唐代外圆内方的铜镜。铜镜的直径是24
cm。外面的圆与内部的正方形之间的面积是多少?
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
课堂练习,内化应用
拓展练习。
2
右图两个正方形的边长都是2分米,比一比两个正方形中
阴影部分的面积。
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
全课总结,畅谈收获
说一说:这节课你有什么收获和体会?
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
板书设计
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
多元化评价
关注学生学习结果
让学生树立自信心
更关注情感与态度
体验学习数学的乐趣
抓纲据本重分析
以生为本定方向
巧设冲突活过程
多维反思促发展
总结与反思
小学数学六年级上册第五单元《圆》的例3
谢谢聆听
,
敬请指导!
