13.3.2.1 等边三角形的性质与判定课件(27张PPT)
文档属性
| 名称 | 13.3.2.1 等边三角形的性质与判定课件(27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-25 07:01:44 | ||
图片预览






文档简介
第十三章 轴对称
13.3 等腰三角形
13.3.2 等边三角形
第1课时 等边三角形的性质与判定
2020年秋人教版数学八年级上册精品课件
学习目标
1
2
能运用等边三角形的性质和判定进行计算和证明.(难点)
探索等边三角形的性质和判定.(重点)
新课导入
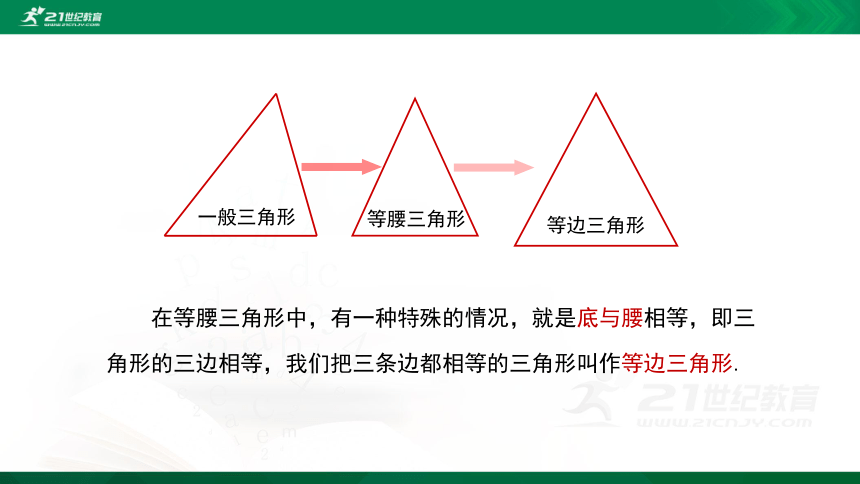
等腰三角形
等边三角形
一般三角形
在等腰三角形中,有一种特殊的情况,就是底与腰相等,即三角形的三边相等,我们把三条边都相等的三角形叫作等边三角形.
知识讲解
1、等边三角形的性质
A
B
C
A
B
C
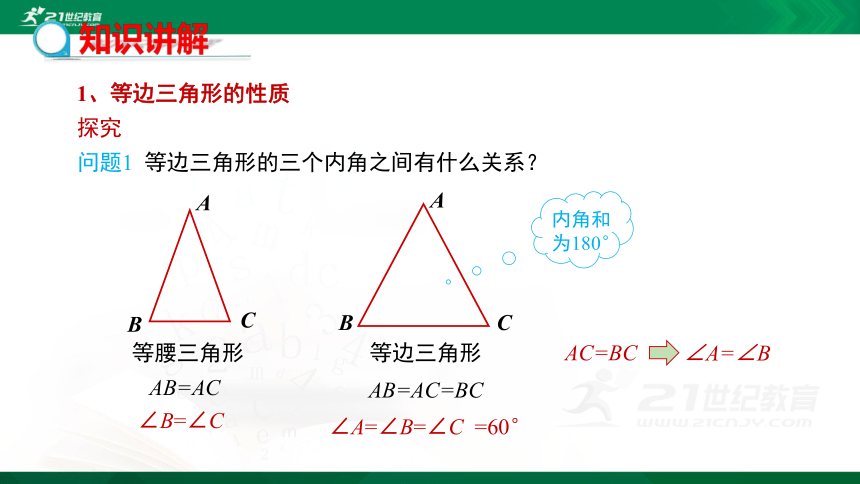
问题1 等边三角形的三个内角之间有什么关系?
等腰三角形
AB=AC
∠B=∠C
等边三角形
AB=AC=BC
AC=BC
∠A=∠B
∠A=∠B=∠C
内角和
为180°
=60°
探究
结论:等边三角形的三个内角都相等,并且每一 个角都等于60°.
已知:AB=AC=BC ,
求证:∠A= ∠ B=∠C= 60°.
证明: ∵AB=AC.
∴∠B=∠C .(等边对等角)
同理 ∠A=∠C .
∴∠A=∠B=∠C.
∵ ∠A+∠B+∠C=180°,
∴ ∠A= ∠B= ∠C=60 °.
A
B
C
A
B
C
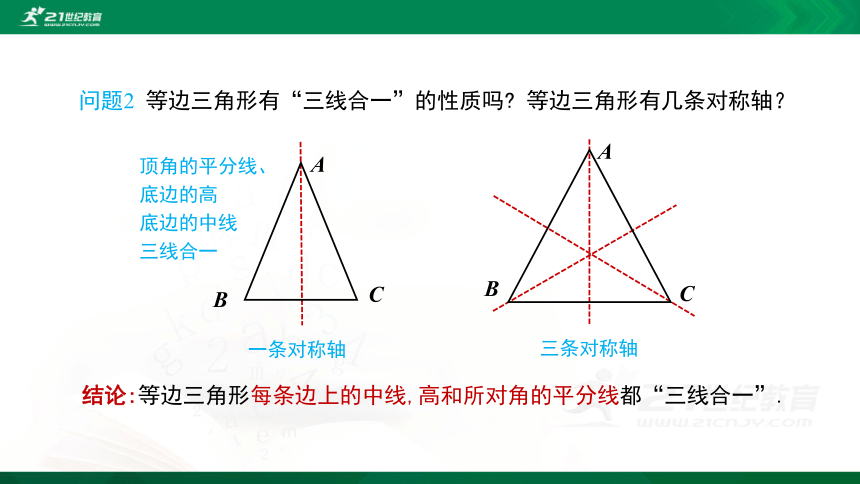
问题2 等边三角形有“三线合一”的性质吗? 等边三角形有几条对称轴?
结论:等边三角形每条边上的中线,高和所对角的平分线都“三线合一”.
顶角的平分线、底边的高
底边的中线
三线合一
一条对称轴
三条对称轴
总结
图形
等腰三角形
性 质
每一边上的中线、高和这一边所对的角的平分线互相重合
三个角都相等,
对称轴(3条)
等边三角形
对称轴(1条)
两个底角相等
底边上的中线、高和顶角的平分线互相重合
且都是60?
两条边相等
三条边都相等
例1 如图,△ABC是等边三角形,E是AC上一点,D是BC延长线上一点,连接BE,DE,若∠ABE=40°,BE=DE,求∠CED的度数.
解:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°.
∵∠ABE=40°,
∴∠EBC=∠ABC-∠ABE
=60°-40°=20°.
∵BE=DE,
∴∠D=∠EBC=20°,
∴∠CED=∠ACB-∠D=40°.
总结:等边三角形是特殊的三角形,它的三个内角都是60°,这个性质常应用在求三角形角度的问题上,一般需结合“等边对等角”、三角形的内角和与外角的性质.
例2 △ABC为正三角形,点M是BC边上任意一点,点N是CA边上任意一点,且BM=CN,BN与AM相交于Q点,∠BQM等于多少度?
解:∵△ABC为正三角形,
∴∠ABC=∠C=∠BAC=60°,AB=BC.
又∵BM=CN,
∴△AMB≌△BNC(SAS),
∴∠BAM=∠CBN,
∴∠BQM=∠ABQ+∠BAM
=∠ABQ+∠CBN=∠ABC=60°.
总结:此题属于等边三角形与全等三角形的综合运用,一般是利
用等边三角形的性质判定三角形全等,而后利用全等及等边三角
形的性质,求角度或证明边相等.
2、等边三角形的判定
图形
等腰三角形
判 定
三个角都相等的三角形是等边三角形
等边三角形
两个角相等的三角形是等腰
三角形
两条边相等的三角形是等腰三角形
三条边都相等的三角形是等边三角形
小明认为还有第三种方法“两条边相等且有一个角是60°的三角形也是等边三角形”,你同意吗?
等边三角形的判定方法:
有一个角是60°的等腰三角形是等边三角形.
根据条件判断下列三角形是否为等边三角形.
(1)
(2)
(6)
(5)
不
是
是
是
是
是
(4)
(3)
不一定
是
例3 如图,在等边三角形ABC中,DE∥BC,
求证:△ADE是等边三角形.
A
C
B
D
E
证明:
∵ △ABC是等边三角形,
∴ ∠A= ∠B= ∠C.
∵ DE//BC,
∴ ∠ADE= ∠B, ∠ AED= ∠C.
∴ ∠A= ∠ADE= ∠ AED.
∴ △ADE是等边三角形.
想一想:本题还有其他证法吗?
证明:∵ △ABC 是等边三角形,
∴ ∠A =∠ABC =∠ACB =60°.
∵ DE∥BC,
∴ ∠ABC =∠ADE,
∠ACB =∠AED.
∴ ∠A =∠ADE =∠AED.
∴ △ADE 是等边三角形.
变式1 若点D、E 在边AB、AC 的延长线上,且DE∥BC,结论还成立吗?
A
D
E
B
C
变式2 若点D、E 在边AB、AC 的反向延长线上,且DE∥BC,结论依然成立吗?
证明: ∵ △ABC 是等边三角形,
∴ ∠BAC =∠B =∠C =60°.
∵ DE∥BC,
∴ ∠B =∠D,∠C =∠E.
∴ ∠EAD =∠D =∠E.
∴ △ADE 是等边三角形.
A
D
E
B
C
变式3 上题中,若将条件DE∥BC改为AD=AE, △ADE还是等边三角形吗?试说明理由.
A
C
B
D
E
证明:
∵ △ABC是等边三角形,
∴ ∠A= ∠B= ∠C.
∵ AD=AE,
∴ ∠ADE= ∠B, ∠ AED= ∠C.
∴ ∠A= ∠ADE= ∠ AED.
∴ △ADE是等边三角形.
例4 等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形?试证明你的结论.
解:△APQ为等边三角形.
证明如下:
∵△ABC为等边三角形,
∴AB=AC.
∵BP=CQ,∠ABP=∠ACQ,
∴△ABP≌△ACQ(SAS),∴AP=AQ,∠BAP=∠CAQ.
∵∠BAC=∠BAP+∠PAC=60°,
∴∠PAQ=∠CAQ+∠PAC=60°,
∴△APQ是等边三角形.
总结:判定一个三角形是等边三角形有以下方法:一是证明三角
形三条边相等;二是证明三角形三个内角相等;三是先证明三角
形是等腰三角形,再证明有一个内角等于60°.
随堂训练
2.如图,等边三角形ABC的三条角平分线交于点O,DE∥BC,则这个图形中的等腰三角形共有( )
A. 4个 B. 5个
C. 6个 D. 7个
D
A
C
B
D
E
O
1.等边三角形的两条高线相交成钝角的度数是( )
A.105° B.120° C.135° D.150°
B
3、在等边△ABC中,BD平分∠ABC,BD=BF,则∠CDF的度数
是 ( )
A.10° B.15°
C.20° D.25°
4、如图,△ABC和△ADE都是等边三角形,
已知△ABC的周长为18cm,EC =2cm,则
△ADE的周长是 cm.
A
C
B
D
E
12
B
5.如图,在△ABC中,∠ACB=90°,∠CAB=30°,以 AB 为边在△ABC 外作等边△ABD,E是AB的中点,连接CE并延长交AD于F.
求证:△AEF≌△BEC.
证明:∵△ABD是等边三角形,
∴∠DAB=60°,
∵∠CAB=30°,∠ACB=90°,
∴∠EBC=180°?90°?30°=60°,∴∠FAE=∠EBC.
∵E为AB的中点,∴AE=BE.
又∵ ∠AEF=∠BEC,
∴△AEF≌△BEC(ASA).
?
课堂小结
等边三角形
定义
底=腰
?
特殊性
性质
特殊性
边
三边相等
角
三个角都等于60 °
轴对称性
轴对称图形,每条边上都具有“三线合一”性质
判定
特殊性
三边法
三角法
等腰三角形法
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
13.3 等腰三角形
13.3.2 等边三角形
第1课时 等边三角形的性质与判定
2020年秋人教版数学八年级上册精品课件
学习目标
1
2
能运用等边三角形的性质和判定进行计算和证明.(难点)
探索等边三角形的性质和判定.(重点)
新课导入
等腰三角形
等边三角形
一般三角形
在等腰三角形中,有一种特殊的情况,就是底与腰相等,即三角形的三边相等,我们把三条边都相等的三角形叫作等边三角形.
知识讲解
1、等边三角形的性质
A
B
C
A
B
C
问题1 等边三角形的三个内角之间有什么关系?
等腰三角形
AB=AC
∠B=∠C
等边三角形
AB=AC=BC
AC=BC
∠A=∠B
∠A=∠B=∠C
内角和
为180°
=60°
探究
结论:等边三角形的三个内角都相等,并且每一 个角都等于60°.
已知:AB=AC=BC ,
求证:∠A= ∠ B=∠C= 60°.
证明: ∵AB=AC.
∴∠B=∠C .(等边对等角)
同理 ∠A=∠C .
∴∠A=∠B=∠C.
∵ ∠A+∠B+∠C=180°,
∴ ∠A= ∠B= ∠C=60 °.
A
B
C
A
B
C
问题2 等边三角形有“三线合一”的性质吗? 等边三角形有几条对称轴?
结论:等边三角形每条边上的中线,高和所对角的平分线都“三线合一”.
顶角的平分线、底边的高
底边的中线
三线合一
一条对称轴
三条对称轴
总结
图形
等腰三角形
性 质
每一边上的中线、高和这一边所对的角的平分线互相重合
三个角都相等,
对称轴(3条)
等边三角形
对称轴(1条)
两个底角相等
底边上的中线、高和顶角的平分线互相重合
且都是60?
两条边相等
三条边都相等
例1 如图,△ABC是等边三角形,E是AC上一点,D是BC延长线上一点,连接BE,DE,若∠ABE=40°,BE=DE,求∠CED的度数.
解:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°.
∵∠ABE=40°,
∴∠EBC=∠ABC-∠ABE
=60°-40°=20°.
∵BE=DE,
∴∠D=∠EBC=20°,
∴∠CED=∠ACB-∠D=40°.
总结:等边三角形是特殊的三角形,它的三个内角都是60°,这个性质常应用在求三角形角度的问题上,一般需结合“等边对等角”、三角形的内角和与外角的性质.
例2 △ABC为正三角形,点M是BC边上任意一点,点N是CA边上任意一点,且BM=CN,BN与AM相交于Q点,∠BQM等于多少度?
解:∵△ABC为正三角形,
∴∠ABC=∠C=∠BAC=60°,AB=BC.
又∵BM=CN,
∴△AMB≌△BNC(SAS),
∴∠BAM=∠CBN,
∴∠BQM=∠ABQ+∠BAM
=∠ABQ+∠CBN=∠ABC=60°.
总结:此题属于等边三角形与全等三角形的综合运用,一般是利
用等边三角形的性质判定三角形全等,而后利用全等及等边三角
形的性质,求角度或证明边相等.
2、等边三角形的判定
图形
等腰三角形
判 定
三个角都相等的三角形是等边三角形
等边三角形
两个角相等的三角形是等腰
三角形
两条边相等的三角形是等腰三角形
三条边都相等的三角形是等边三角形
小明认为还有第三种方法“两条边相等且有一个角是60°的三角形也是等边三角形”,你同意吗?
等边三角形的判定方法:
有一个角是60°的等腰三角形是等边三角形.
根据条件判断下列三角形是否为等边三角形.
(1)
(2)
(6)
(5)
不
是
是
是
是
是
(4)
(3)
不一定
是
例3 如图,在等边三角形ABC中,DE∥BC,
求证:△ADE是等边三角形.
A
C
B
D
E
证明:
∵ △ABC是等边三角形,
∴ ∠A= ∠B= ∠C.
∵ DE//BC,
∴ ∠ADE= ∠B, ∠ AED= ∠C.
∴ ∠A= ∠ADE= ∠ AED.
∴ △ADE是等边三角形.
想一想:本题还有其他证法吗?
证明:∵ △ABC 是等边三角形,
∴ ∠A =∠ABC =∠ACB =60°.
∵ DE∥BC,
∴ ∠ABC =∠ADE,
∠ACB =∠AED.
∴ ∠A =∠ADE =∠AED.
∴ △ADE 是等边三角形.
变式1 若点D、E 在边AB、AC 的延长线上,且DE∥BC,结论还成立吗?
A
D
E
B
C
变式2 若点D、E 在边AB、AC 的反向延长线上,且DE∥BC,结论依然成立吗?
证明: ∵ △ABC 是等边三角形,
∴ ∠BAC =∠B =∠C =60°.
∵ DE∥BC,
∴ ∠B =∠D,∠C =∠E.
∴ ∠EAD =∠D =∠E.
∴ △ADE 是等边三角形.
A
D
E
B
C
变式3 上题中,若将条件DE∥BC改为AD=AE, △ADE还是等边三角形吗?试说明理由.
A
C
B
D
E
证明:
∵ △ABC是等边三角形,
∴ ∠A= ∠B= ∠C.
∵ AD=AE,
∴ ∠ADE= ∠B, ∠ AED= ∠C.
∴ ∠A= ∠ADE= ∠ AED.
∴ △ADE是等边三角形.
例4 等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形?试证明你的结论.
解:△APQ为等边三角形.
证明如下:
∵△ABC为等边三角形,
∴AB=AC.
∵BP=CQ,∠ABP=∠ACQ,
∴△ABP≌△ACQ(SAS),∴AP=AQ,∠BAP=∠CAQ.
∵∠BAC=∠BAP+∠PAC=60°,
∴∠PAQ=∠CAQ+∠PAC=60°,
∴△APQ是等边三角形.
总结:判定一个三角形是等边三角形有以下方法:一是证明三角
形三条边相等;二是证明三角形三个内角相等;三是先证明三角
形是等腰三角形,再证明有一个内角等于60°.
随堂训练
2.如图,等边三角形ABC的三条角平分线交于点O,DE∥BC,则这个图形中的等腰三角形共有( )
A. 4个 B. 5个
C. 6个 D. 7个
D
A
C
B
D
E
O
1.等边三角形的两条高线相交成钝角的度数是( )
A.105° B.120° C.135° D.150°
B
3、在等边△ABC中,BD平分∠ABC,BD=BF,则∠CDF的度数
是 ( )
A.10° B.15°
C.20° D.25°
4、如图,△ABC和△ADE都是等边三角形,
已知△ABC的周长为18cm,EC =2cm,则
△ADE的周长是 cm.
A
C
B
D
E
12
B
5.如图,在△ABC中,∠ACB=90°,∠CAB=30°,以 AB 为边在△ABC 外作等边△ABD,E是AB的中点,连接CE并延长交AD于F.
求证:△AEF≌△BEC.
证明:∵△ABD是等边三角形,
∴∠DAB=60°,
∵∠CAB=30°,∠ACB=90°,
∴∠EBC=180°?90°?30°=60°,∴∠FAE=∠EBC.
∵E为AB的中点,∴AE=BE.
又∵ ∠AEF=∠BEC,
∴△AEF≌△BEC(ASA).
?
课堂小结
等边三角形
定义
底=腰
?
特殊性
性质
特殊性
边
三边相等
角
三个角都等于60 °
轴对称性
轴对称图形,每条边上都具有“三线合一”性质
判定
特殊性
三边法
三角法
等腰三角形法
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
