人教版九年级上册数学23.1图形的旋转课件(共26张PPT)
文档属性
| 名称 | 人教版九年级上册数学23.1图形的旋转课件(共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 904.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-24 14:26:33 | ||
图片预览






文档简介
(共26张PPT)
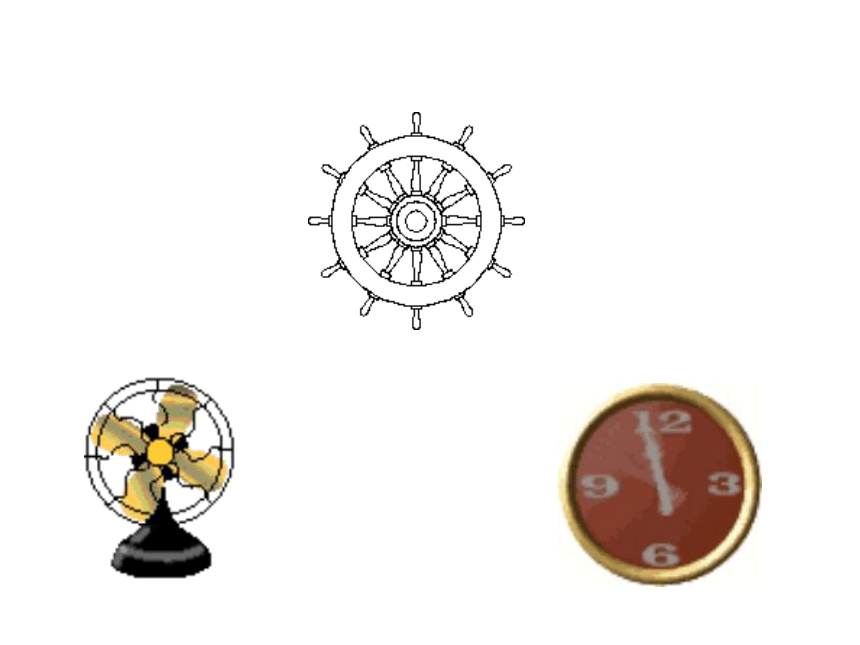
你能说一说风车、摩天轮、时钟的运动有什么共同特征吗?
它们都可以进行这样的运动
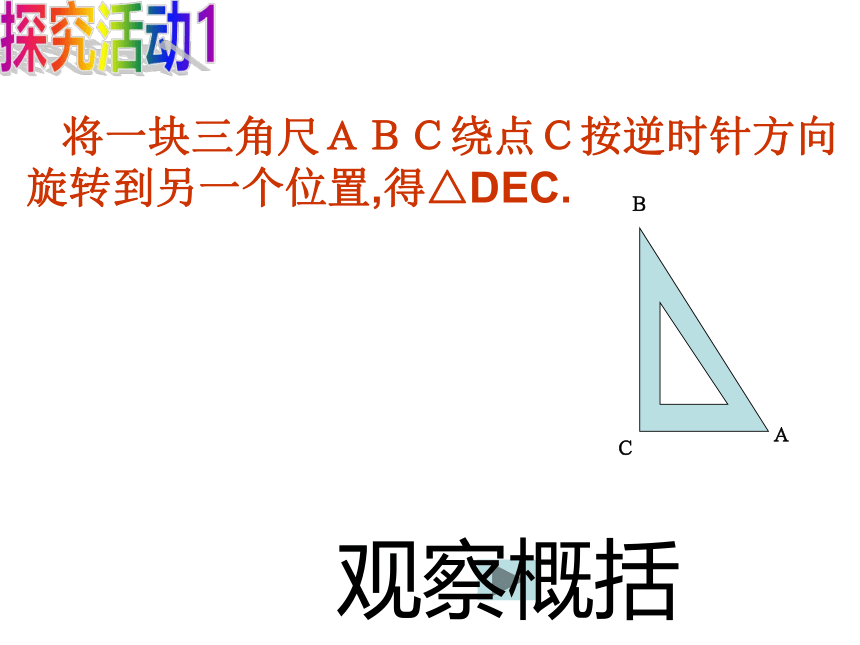
将一块三角尺ABC绕点C按逆时针方向
旋转到另一个位置,得△DEC.
B
C
A
观察概括
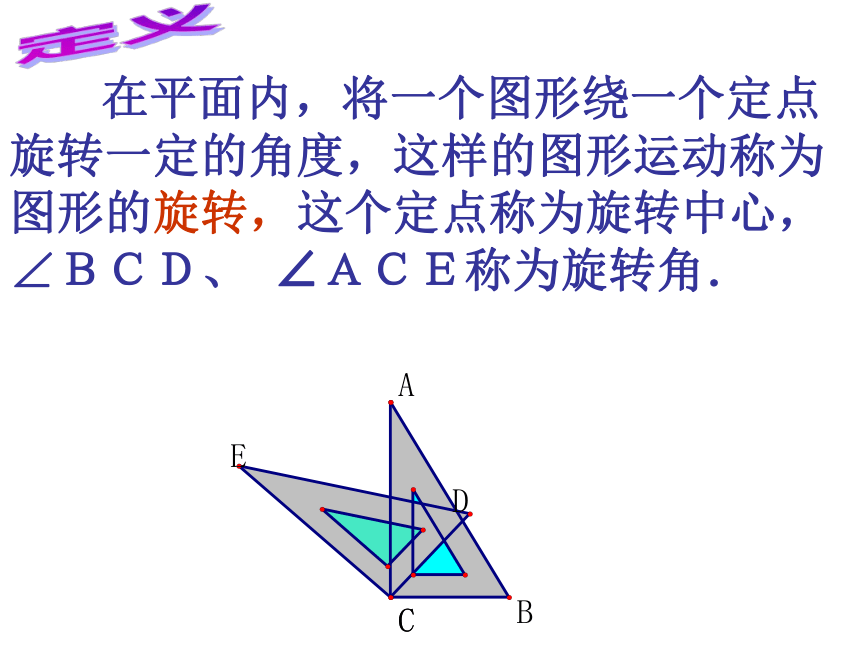
在平面内,将一个图形绕一个定点
旋转一定的角度,这样的图形运动称为
图形的旋转,这个定点称为旋转中心,
∠BCD、
∠ACE称为旋转角.
旋转中心是点______
旋转的角度是
______
如图,是△AOB绕点O按逆时针方向旋转450所得的。
O
450
D'
D
A'
A
B
O
B'
旋转角为
下图是由正方形ABCD逆时针旋转而成。
(1)旋转中心是__________
(2)
旋转的角度是_________
点A
450
(3)
若正方形的边长是1,则C’D=_________
C'
D'
B'
B
A
C
D
旋转前、后的图形全等。
对应点到旋转中心的距离相等。
每一对对应点与旋转中心的连线所成的角彼此相等。
⑸.连接A’B’
线段A’B’就是线段AB绕点O按逆时针方向旋转100°后的对应线段。
A'
B'
B
A
O
D
C
1.已知线段AB和点O,画出AB绕点O逆时针旋转100°后的图形。
⑴.连接OA
⑵.作∠AOC=100°,在OC上截取OA'=OA
⑷.作∠BOD=100°,在OD上截取OB'=OB
⑶.连接OB
注:作旋转后的图形可以转化为作旋转后的对应点
练习1:
如图:将RtΔABCRtΔADE怎样旋转就能重合?旋转了多少度?
练习2:
如图:有两个正方形ABCD和CDEF,点O为CD的中点,要将正方形DEFC旋转到正方形ABCD的位置,共有
个旋转中心.
练习3:
下列图形中,哪些是一个长方形由另一个长方形绕中心按顺时针方向旋转90°后形成的?
性质运用3:
课本P76
练习2
性质运用3:
如图,△ABC是等边三角形,D是BC上一
点,△ABD经过旋转后到达△ACD’的位置。
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是AB的中点,那么经过上述旋转后,点M转到了什么位置?
M'
M
D'
C
A
B
D
拓展应用1:
香港特别行政区区旗中央的紫荆花图案由5个相同的花瓣组成,它是由其中一瓣经过几次旋转得到的?
拓展应用2:
O
A
B
如图:画出AB绕点O旋转后,线段AB的对应线段是A′B′,试确定旋转中心点O的位置.
1.旋转中心与对应点满足什么样的关系?
2.你能找出到A、A′两点距离相等的点吗?
你能找出到B、B′两点距离相等的点吗?
3.你能找出同时满足上面两个条件的点吗?
A′
B′
拓展应用3:
图形的旋转有三要素:
一、旋转中心
二、旋转方向
三、旋转角
下列现象中属于旋转的有(
)个.
①地下水位逐年下降;②传送带的运动;③方向盘的转动;
④水龙头开关的动;⑤钟摆的运动;
⑥荡秋千.
A.2
B.3
C.4
D.5
你能说一说风车、摩天轮、时钟的运动有什么共同特征吗?
它们都可以进行这样的运动
将一块三角尺ABC绕点C按逆时针方向
旋转到另一个位置,得△DEC.
B
C
A
观察概括
在平面内,将一个图形绕一个定点
旋转一定的角度,这样的图形运动称为
图形的旋转,这个定点称为旋转中心,
∠BCD、
∠ACE称为旋转角.
旋转中心是点______
旋转的角度是
______
如图,是△AOB绕点O按逆时针方向旋转450所得的。
O
450
D'
D
A'
A
B
O
B'
旋转角为
下图是由正方形ABCD逆时针旋转而成。
(1)旋转中心是__________
(2)
旋转的角度是_________
点A
450
(3)
若正方形的边长是1,则C’D=_________
C'
D'
B'
B
A
C
D
旋转前、后的图形全等。
对应点到旋转中心的距离相等。
每一对对应点与旋转中心的连线所成的角彼此相等。
⑸.连接A’B’
线段A’B’就是线段AB绕点O按逆时针方向旋转100°后的对应线段。
A'
B'
B
A
O
D
C
1.已知线段AB和点O,画出AB绕点O逆时针旋转100°后的图形。
⑴.连接OA
⑵.作∠AOC=100°,在OC上截取OA'=OA
⑷.作∠BOD=100°,在OD上截取OB'=OB
⑶.连接OB
注:作旋转后的图形可以转化为作旋转后的对应点
练习1:
如图:将RtΔABCRtΔADE怎样旋转就能重合?旋转了多少度?
练习2:
如图:有两个正方形ABCD和CDEF,点O为CD的中点,要将正方形DEFC旋转到正方形ABCD的位置,共有
个旋转中心.
练习3:
下列图形中,哪些是一个长方形由另一个长方形绕中心按顺时针方向旋转90°后形成的?
性质运用3:
课本P76
练习2
性质运用3:
如图,△ABC是等边三角形,D是BC上一
点,△ABD经过旋转后到达△ACD’的位置。
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是AB的中点,那么经过上述旋转后,点M转到了什么位置?
M'
M
D'
C
A
B
D
拓展应用1:
香港特别行政区区旗中央的紫荆花图案由5个相同的花瓣组成,它是由其中一瓣经过几次旋转得到的?
拓展应用2:
O
A
B
如图:画出AB绕点O旋转后,线段AB的对应线段是A′B′,试确定旋转中心点O的位置.
1.旋转中心与对应点满足什么样的关系?
2.你能找出到A、A′两点距离相等的点吗?
你能找出到B、B′两点距离相等的点吗?
3.你能找出同时满足上面两个条件的点吗?
A′
B′
拓展应用3:
图形的旋转有三要素:
一、旋转中心
二、旋转方向
三、旋转角
下列现象中属于旋转的有(
)个.
①地下水位逐年下降;②传送带的运动;③方向盘的转动;
④水龙头开关的动;⑤钟摆的运动;
⑥荡秋千.
A.2
B.3
C.4
D.5
同课章节目录
