2020年秋苏科版九年级数学上册第一章《一元二次方程》单元培优测试卷(Word版,含解析)
文档属性
| 名称 | 2020年秋苏科版九年级数学上册第一章《一元二次方程》单元培优测试卷(Word版,含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 87.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-24 00:00:00 | ||
图片预览



文档简介
2020年秋苏科版九年级数学上册第一章一元二次方程单元培优测试卷
一、选择题(共10题;共30分)
1.下列方程中是关于x的一元二次方程的是(???
)
A.?B.ax2+bx+c=0?C.(x-1)(x+
2)=1???D.3x2-2xy-5y2=0
2.用配方法解一元二次方程x2-8x+11=0,此方程可化为(???
)
A.(x-4)2=5????B.(x+4)?=5?????C.(x-4)?=27?????D.(x+4)?=27
3.一元二次方程x2﹣2x﹣1=0的根的情况为(??
)
A.有两个相等的实数根?B.有两个不相等的实数根?C.只有一个实数根???D.没有实数根
4.已知一元二次方程x2﹣4x+m=0有一个根为2,则另一根为(??
)
A.﹣4?
B.﹣2???C.4????D.2
5.从正方形铁片,截去2cm宽的一条长方形,余下的矩形的面积是
,则原来的正方形铁片的面积是(
)
A.?????B.?????C.????D.
6.三角形的两边长分别为3米和6米,第三边的长是方程x2﹣6x+8=0的一个根,则这个三角形的周长为(
??)
A.11????B.12????C.11或
13????D.13
7.如果关于x的一元二次方程
有两个实数根,那么
的取值范围是(???
)
A.????B.
且
??C.
且
??D.
8.菱形ABCD的一条对角线长为6,另一条对角线的长为方程y2﹣2y﹣8=0的一个根,则菱形ABCD的面积为(?
)
A.10?????B.12????C.10或12????D.24
9.某公司今年1月的营业额为250万元,按计划第1季度的营业额要达到900万元,设该公司2、3月的营业额的月平均增长率为
.根据题意列方程正确的是(???
)
A.?
?B.
C.??D.
10.若m是一元二次方程x2-4x-1=0的一个根,则代数式4m-m?的值为(????
)
A.1??????B.-1????C.2????D.-22
二、填空题(共6题;共24分)
11.若
,则
________.
12.一元二次方程
的解为________.
13.设
,
是方程
的两个实数根,则
的值为________.
14.已知关于x的一元二次方程
有一个根为
,则a的值为________.
15.某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是21,则每个支干长出________.
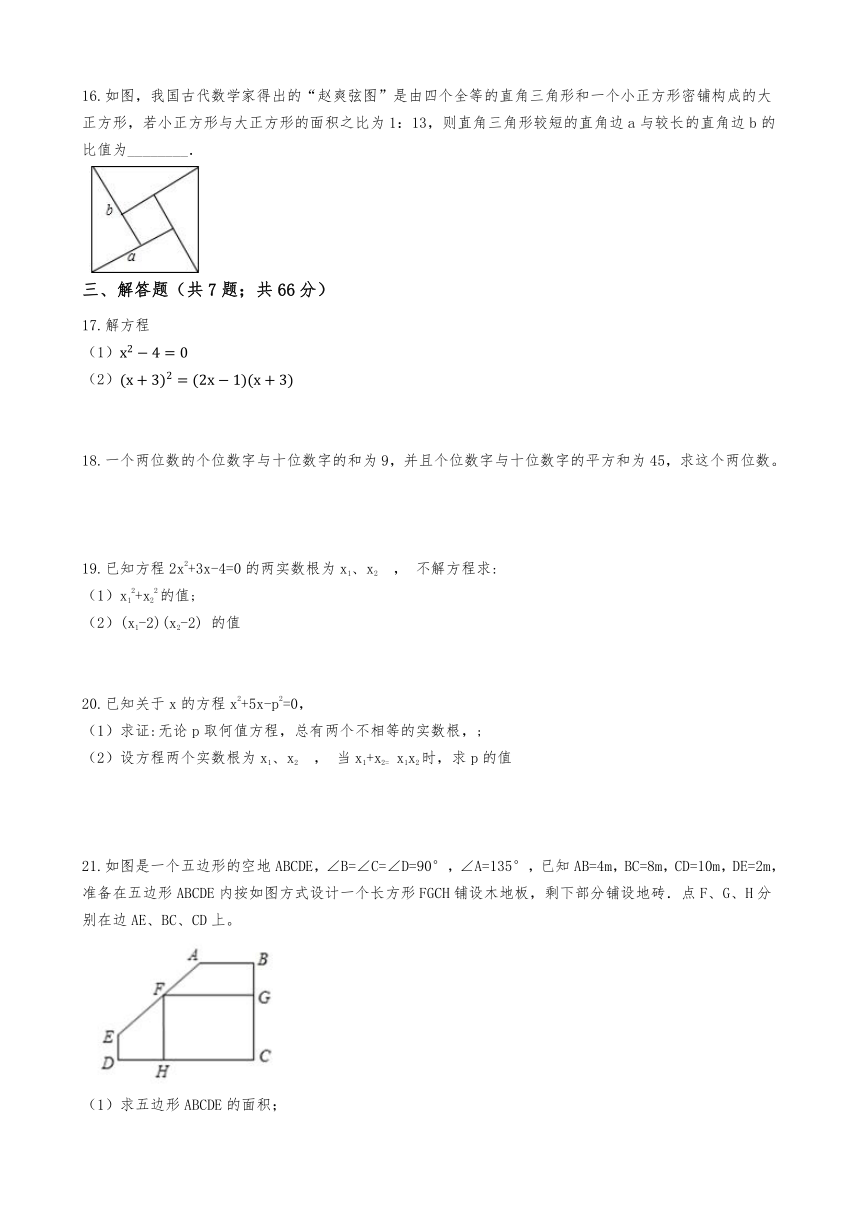
16.如图,我国古代数学家得出的“赵爽弦图”是由四个全等的直角三角形和一个小正方形密铺构成的大正方形,若小正方形与大正方形的面积之比为1:13,则直角三角形较短的直角边a与较长的直角边b的比值为________.
三、解答题(共7题;共66分)
17.解方程
(1)
(2)
18.一个两位数的个位数字与十位数字的和为9,并且个位数字与十位数字的平方和为45,求这个两位数。
19.已知方程2x2+3x-4=0的两实数根为x1、x2
,
不解方程求:
(1)x12+x22的值;
(2)(x1-2)(x2-2)
的值
20.已知关于x的方程x2+5x-p2=0,
(1)求证:无论p取何值方程,总有两个不相等的实数根,;
(2)设方程两个实数根为x1、x2
,
当x1+x2=
x1x2时,求p的值
21.如图是一个五边形的空地ABCDE,∠B=∠C=∠D=90°,∠A=135°,已知AB=4m,BC=8m,CD=10m,DE=2m,准备在五边形ABCDE内按如图方式设计一个长方形FGCH铺设木地板,剩下部分铺设地砖.点F、G、H分别在边AE、BC、CD上。
(1)求五边形ABCDE的面积;
(2)若长方形FGCH的面积为35m?,求BG的长。
(3)若铺设木地板的成本为每平方米200元,铺设地砖的成本为每平方米100元,投资7300元能否完成地面铺设?通过计算说明。
22.宾馆有50间房供游客居住,原定价每间房每天190元,当每间房每天定价为180元时,宾馆会住满;当每间房每天的定价每增加10元时,就会空闲一间房(物价部门规定,此类宾馆的入住费用不得超过原定价的1.5倍)。如果有游客居住,宾馆需对居住的每间房每天支出20元的费用。
(1)如果每间房当天的定价比房间住满时的房价增加x元时,宾馆________间房有游客居住(用含x的代数式表示);
(2)当房价定为多少元时,宾馆当天的利润为9450元?
23.如图,已知直线
与x轴交于点A,与y轴交于点B,线段
的长是方程
的一个根,
.请解答下列问题:
(1)求点A,B的坐标;
(2)直线
交x轴负半轴于点E,交y轴正半轴于点F,交直线
于点C.若C是
的中点,
,反比例函数
图象的一支经过点C,求k的值;
(3)在(2)的条件下,过点C作
,垂足为D,点M在直线
上,点N在直线
上.坐标平面内是否存在点P,使以D,M,N,P为顶点的四边形是正方形?若存在,请写出点P的个数,并直接写出其中两个点P的坐标;若不存在,请说明理由.
答案
一、选择题
1.解:A.含有分式,故不是;
B.没有说明a≠0,则不是;
C.是一元二次方程;
D.含有两个未知数,故不是;
故答案为:C.
2.解:用配方法解一元二次方程x2-8x+11=0
移项:x2-8x=-11
方程两边同时加上x系数绝对值一半的平方:x2-8x+42=-11+42
即:
(x-4)?=5
故答案为:A
3.解:根据题意△=(﹣2)2﹣4×(﹣1)=8>0,
所以方程有两个不相等的实数根.
故答案为:B.
4.解:设方程的另一个根为x1
,
根据题意得:2+x1=4,
解得:x1=2.
故答案为:D.
5.解:设正方形的边长是xcm,根据题意得x(x-2)=48,
解得
(舍去),
,
那么原正方形铁片的面积是8×8=64cm?.
故答案为:D.
6.解:∵x2﹣6x+8=0,即(x﹣2)(x﹣4)=0,
∴x﹣2=0或x﹣4=0,
解得:x=2或x=4,
若x=2,则三角形的三边2+3<6,构不成三角形,舍去;
当x=4时,这个三角形的周长为3+4+6=13,
故答案为:D.
7.解:∵关于x的一元二次方程kx2-3x+1=0有两个实数根,
∴△=(-3)2-4×k×1≥0且k≠0,
解得k≤
且k≠0,
故答案为:C.
8.∵y2﹣2y﹣8=0,
∴(y+2)(y﹣4)=0,
∴y+2=0或y﹣4=0,
解得:y=﹣2(舍)或y=4,
∴菱形ABCD的面积=
×6×4=12,
故答案为:B.
9.解:根据题意列方程得:
.
故答案为:D.
10.解:由意义得:
m2-4m-1=0,
∴m2-4m=1,
∴
4m-m?
=-1.
故答案为:B.
二、填空题
11.解:
∴
或
又∵
,
∴
12.
当x-2=0时,x=2,
当x-2≠0时,4x=1,x=
,
故答案为:x=
或x=2.
13.解:由方程
可知
,
.
故答案为:
14.
代入方程得:
解得:
∵
是关于
的一元二次方程
∴
∴
故答案为-1
15.解:设每个支干长出x个小支干,
根据题意得:1+x+x2=21,
解得:x1=﹣5(舍去),x2=4.
故答案为:4个小支干.
16.∵小正方形与大正方形的面积之比为1:13,
∴设大正方形的面积是13,
∴c2=13,
∴a2+b2=c2=13,
∵直角三角形的面积是
=3,
又∵直角三角形的面积是
ab=3,
∴ab=6,
∴(a+b)2=a2+b2+2ab=c2+2ab=13+2×6=13+12=25,
∴a+b=5.
则a、b是方程x2﹣5x+6=0的两个根,
故b=3,a=2,
∴
.
故答案是:2:3.
三、解答题
17.
(1)解:移项得
两边直接开平方得
,
(2)解:移项得
提取公因式得
即
∴
或
解得
,
18.
解:设这个两位数的个位数字为x,则十位数字为(9-x),根据题意得
x2+(9-x)2=45
解之:x1=3,x2=6.
当x=3时9-x=6;
当x=6时9-x=3.
∴这个两位数为63或36.
19.
(1)解:根据题意得
(2)解:由(1)可知
所以:
20.
(1)证明:
因为无论p取何值时,总有p2≥0,
所以,25+
p2>0,
所以无论p取何值方程,总有两个不相等的实数根,
(2)解:由题意得,x1+x2=-5
,
x1x2=-
p2
因为,x1+x2=
x1x2
,
所以,-5=-
p2
所以,
.
21.
(1)解:如图,过E、A分别作EM⊥BC于M,作AN⊥EM于N,
则∠EAN=∠AEN=45°,
∴AN=EN,
∵MN=AB,EM=CD,
∴EN=EM-MN=DC-AB=10-4=6(m),
∴AN=6(m),
∴S五边形ABCDE=S梯形ABME+S长方形EMCD=
?(4+10)×6+2×10=62(m2)
(2)解:设BG=xm,则FG=(4+x)m,CG=(8-x)m,
根据题意,得(4+x)(8-x)=35,
解得:x1=1,x2=3
∴BG的长为1m或3m
(3)解:设BG=ym,
由题意,得200×(4+y)(8-y)+100×[62-(4+y)(8-y)]=7300,
化简,得y2-4y-21=0,
解得:y1=7,y2=-3均不合题意,
∴投资7300元不能完成地面铺设
22.
(1)50-
(2)解:根据题意,得:(180+x-20)(50-
)=9450
整理得x?-340x+14500=0,解得x1=50,x2=290(2分)(x2不符合题意,舍去),
∴房价定为230元
答:当房价定为230元时,宾馆当天的利润为9450元。
(1)根据题意,
当每间房每天的定价每增加10元时,就会空闲一间房
,即为空闲的房间,总的房间为50,则为旅客居住房间。
故答案为:.
23.
(1)解:∵线段
的长是方程
的一个根,
解得:x=9或-2(舍),而点A在x轴正半轴,
∴A(9,0),
∵
,
∴B(0,
);
(2)解:∵
,
∴E(-6,0),
设直线AB的表达式为y=kx+b,将A和B代入,
得:
,解得:
,
∴AB的表达式为:
,
∵点C是EF的中点,
∴点C的横坐标为-3,代入AB中,y=6,
则C(-3,6),
∵反比例函数
经过点C,
则k=-3×6=-18;
(3)解:存在点P,使以D,M,N,P为顶点的四边形是正方形,
如图,共有5种情况,
在四边形DM1P1N1中,
M1和点A重合,
∴M1(9,0),
此时P1(9,12);
在四边形DP3BN3中,点B和M重合,
可知M在直线y=x+3上,
联立:
,
解得:
,
∴M(1,4),
∴P3(1,0),
同理可得:P2(9,-12),P4(-7,4),P5(-15,0).
故存在点P使以D,M,N,P为顶点的四边形是正方形,
点P的坐标为P1(9,12),P2(9,-12),P3(1,0),P4(-7,4),P5(-15,0).
一、选择题(共10题;共30分)
1.下列方程中是关于x的一元二次方程的是(???
)
A.?B.ax2+bx+c=0?C.(x-1)(x+
2)=1???D.3x2-2xy-5y2=0
2.用配方法解一元二次方程x2-8x+11=0,此方程可化为(???
)
A.(x-4)2=5????B.(x+4)?=5?????C.(x-4)?=27?????D.(x+4)?=27
3.一元二次方程x2﹣2x﹣1=0的根的情况为(??
)
A.有两个相等的实数根?B.有两个不相等的实数根?C.只有一个实数根???D.没有实数根
4.已知一元二次方程x2﹣4x+m=0有一个根为2,则另一根为(??
)
A.﹣4?
B.﹣2???C.4????D.2
5.从正方形铁片,截去2cm宽的一条长方形,余下的矩形的面积是
,则原来的正方形铁片的面积是(
)
A.?????B.?????C.????D.
6.三角形的两边长分别为3米和6米,第三边的长是方程x2﹣6x+8=0的一个根,则这个三角形的周长为(
??)
A.11????B.12????C.11或
13????D.13
7.如果关于x的一元二次方程
有两个实数根,那么
的取值范围是(???
)
A.????B.
且
??C.
且
??D.
8.菱形ABCD的一条对角线长为6,另一条对角线的长为方程y2﹣2y﹣8=0的一个根,则菱形ABCD的面积为(?
)
A.10?????B.12????C.10或12????D.24
9.某公司今年1月的营业额为250万元,按计划第1季度的营业额要达到900万元,设该公司2、3月的营业额的月平均增长率为
.根据题意列方程正确的是(???
)
A.?
?B.
C.??D.
10.若m是一元二次方程x2-4x-1=0的一个根,则代数式4m-m?的值为(????
)
A.1??????B.-1????C.2????D.-22
二、填空题(共6题;共24分)
11.若
,则
________.
12.一元二次方程
的解为________.
13.设
,
是方程
的两个实数根,则
的值为________.
14.已知关于x的一元二次方程
有一个根为
,则a的值为________.
15.某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是21,则每个支干长出________.
16.如图,我国古代数学家得出的“赵爽弦图”是由四个全等的直角三角形和一个小正方形密铺构成的大正方形,若小正方形与大正方形的面积之比为1:13,则直角三角形较短的直角边a与较长的直角边b的比值为________.
三、解答题(共7题;共66分)
17.解方程
(1)
(2)
18.一个两位数的个位数字与十位数字的和为9,并且个位数字与十位数字的平方和为45,求这个两位数。
19.已知方程2x2+3x-4=0的两实数根为x1、x2
,
不解方程求:
(1)x12+x22的值;
(2)(x1-2)(x2-2)
的值
20.已知关于x的方程x2+5x-p2=0,
(1)求证:无论p取何值方程,总有两个不相等的实数根,;
(2)设方程两个实数根为x1、x2
,
当x1+x2=
x1x2时,求p的值
21.如图是一个五边形的空地ABCDE,∠B=∠C=∠D=90°,∠A=135°,已知AB=4m,BC=8m,CD=10m,DE=2m,准备在五边形ABCDE内按如图方式设计一个长方形FGCH铺设木地板,剩下部分铺设地砖.点F、G、H分别在边AE、BC、CD上。
(1)求五边形ABCDE的面积;
(2)若长方形FGCH的面积为35m?,求BG的长。
(3)若铺设木地板的成本为每平方米200元,铺设地砖的成本为每平方米100元,投资7300元能否完成地面铺设?通过计算说明。
22.宾馆有50间房供游客居住,原定价每间房每天190元,当每间房每天定价为180元时,宾馆会住满;当每间房每天的定价每增加10元时,就会空闲一间房(物价部门规定,此类宾馆的入住费用不得超过原定价的1.5倍)。如果有游客居住,宾馆需对居住的每间房每天支出20元的费用。
(1)如果每间房当天的定价比房间住满时的房价增加x元时,宾馆________间房有游客居住(用含x的代数式表示);
(2)当房价定为多少元时,宾馆当天的利润为9450元?
23.如图,已知直线
与x轴交于点A,与y轴交于点B,线段
的长是方程
的一个根,
.请解答下列问题:
(1)求点A,B的坐标;
(2)直线
交x轴负半轴于点E,交y轴正半轴于点F,交直线
于点C.若C是
的中点,
,反比例函数
图象的一支经过点C,求k的值;
(3)在(2)的条件下,过点C作
,垂足为D,点M在直线
上,点N在直线
上.坐标平面内是否存在点P,使以D,M,N,P为顶点的四边形是正方形?若存在,请写出点P的个数,并直接写出其中两个点P的坐标;若不存在,请说明理由.
答案
一、选择题
1.解:A.含有分式,故不是;
B.没有说明a≠0,则不是;
C.是一元二次方程;
D.含有两个未知数,故不是;
故答案为:C.
2.解:用配方法解一元二次方程x2-8x+11=0
移项:x2-8x=-11
方程两边同时加上x系数绝对值一半的平方:x2-8x+42=-11+42
即:
(x-4)?=5
故答案为:A
3.解:根据题意△=(﹣2)2﹣4×(﹣1)=8>0,
所以方程有两个不相等的实数根.
故答案为:B.
4.解:设方程的另一个根为x1
,
根据题意得:2+x1=4,
解得:x1=2.
故答案为:D.
5.解:设正方形的边长是xcm,根据题意得x(x-2)=48,
解得
(舍去),
,
那么原正方形铁片的面积是8×8=64cm?.
故答案为:D.
6.解:∵x2﹣6x+8=0,即(x﹣2)(x﹣4)=0,
∴x﹣2=0或x﹣4=0,
解得:x=2或x=4,
若x=2,则三角形的三边2+3<6,构不成三角形,舍去;
当x=4时,这个三角形的周长为3+4+6=13,
故答案为:D.
7.解:∵关于x的一元二次方程kx2-3x+1=0有两个实数根,
∴△=(-3)2-4×k×1≥0且k≠0,
解得k≤
且k≠0,
故答案为:C.
8.∵y2﹣2y﹣8=0,
∴(y+2)(y﹣4)=0,
∴y+2=0或y﹣4=0,
解得:y=﹣2(舍)或y=4,
∴菱形ABCD的面积=
×6×4=12,
故答案为:B.
9.解:根据题意列方程得:
.
故答案为:D.
10.解:由意义得:
m2-4m-1=0,
∴m2-4m=1,
∴
4m-m?
=-1.
故答案为:B.
二、填空题
11.解:
∴
或
又∵
,
∴
12.
当x-2=0时,x=2,
当x-2≠0时,4x=1,x=
,
故答案为:x=
或x=2.
13.解:由方程
可知
,
.
故答案为:
14.
代入方程得:
解得:
∵
是关于
的一元二次方程
∴
∴
故答案为-1
15.解:设每个支干长出x个小支干,
根据题意得:1+x+x2=21,
解得:x1=﹣5(舍去),x2=4.
故答案为:4个小支干.
16.∵小正方形与大正方形的面积之比为1:13,
∴设大正方形的面积是13,
∴c2=13,
∴a2+b2=c2=13,
∵直角三角形的面积是
=3,
又∵直角三角形的面积是
ab=3,
∴ab=6,
∴(a+b)2=a2+b2+2ab=c2+2ab=13+2×6=13+12=25,
∴a+b=5.
则a、b是方程x2﹣5x+6=0的两个根,
故b=3,a=2,
∴
.
故答案是:2:3.
三、解答题
17.
(1)解:移项得
两边直接开平方得
,
(2)解:移项得
提取公因式得
即
∴
或
解得
,
18.
解:设这个两位数的个位数字为x,则十位数字为(9-x),根据题意得
x2+(9-x)2=45
解之:x1=3,x2=6.
当x=3时9-x=6;
当x=6时9-x=3.
∴这个两位数为63或36.
19.
(1)解:根据题意得
(2)解:由(1)可知
所以:
20.
(1)证明:
因为无论p取何值时,总有p2≥0,
所以,25+
p2>0,
所以无论p取何值方程,总有两个不相等的实数根,
(2)解:由题意得,x1+x2=-5
,
x1x2=-
p2
因为,x1+x2=
x1x2
,
所以,-5=-
p2
所以,
.
21.
(1)解:如图,过E、A分别作EM⊥BC于M,作AN⊥EM于N,
则∠EAN=∠AEN=45°,
∴AN=EN,
∵MN=AB,EM=CD,
∴EN=EM-MN=DC-AB=10-4=6(m),
∴AN=6(m),
∴S五边形ABCDE=S梯形ABME+S长方形EMCD=
?(4+10)×6+2×10=62(m2)
(2)解:设BG=xm,则FG=(4+x)m,CG=(8-x)m,
根据题意,得(4+x)(8-x)=35,
解得:x1=1,x2=3
∴BG的长为1m或3m
(3)解:设BG=ym,
由题意,得200×(4+y)(8-y)+100×[62-(4+y)(8-y)]=7300,
化简,得y2-4y-21=0,
解得:y1=7,y2=-3均不合题意,
∴投资7300元不能完成地面铺设
22.
(1)50-
(2)解:根据题意,得:(180+x-20)(50-
)=9450
整理得x?-340x+14500=0,解得x1=50,x2=290(2分)(x2不符合题意,舍去),
∴房价定为230元
答:当房价定为230元时,宾馆当天的利润为9450元。
(1)根据题意,
当每间房每天的定价每增加10元时,就会空闲一间房
,即为空闲的房间,总的房间为50,则为旅客居住房间。
故答案为:.
23.
(1)解:∵线段
的长是方程
的一个根,
解得:x=9或-2(舍),而点A在x轴正半轴,
∴A(9,0),
∵
,
∴B(0,
);
(2)解:∵
,
∴E(-6,0),
设直线AB的表达式为y=kx+b,将A和B代入,
得:
,解得:
,
∴AB的表达式为:
,
∵点C是EF的中点,
∴点C的横坐标为-3,代入AB中,y=6,
则C(-3,6),
∵反比例函数
经过点C,
则k=-3×6=-18;
(3)解:存在点P,使以D,M,N,P为顶点的四边形是正方形,
如图,共有5种情况,
在四边形DM1P1N1中,
M1和点A重合,
∴M1(9,0),
此时P1(9,12);
在四边形DP3BN3中,点B和M重合,
可知M在直线y=x+3上,
联立:
,
解得:
,
∴M(1,4),
∴P3(1,0),
同理可得:P2(9,-12),P4(-7,4),P5(-15,0).
故存在点P使以D,M,N,P为顶点的四边形是正方形,
点P的坐标为P1(9,12),P2(9,-12),P3(1,0),P4(-7,4),P5(-15,0).
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
