湖南2012高三入学模拟考试--数学
图片预览




文档简介
2012届高三入学考试模拟试卷
数 学
(试卷满分:150分 考试试卷:120分钟)
一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.函数图像的对称轴方程可以是
A. B. C. D.
2.设实数且(其中是虚数单位)为正实数,则的值为
A.-1 B.0 C.0或-1 D.1
3.已知向量、满足且则=
A.10 B.20 C.21 D.30
4.已知,由如右程序框图输出的
A. 0 B. C. 1 D.
5.给定下列四个命题:
①分别与两条异面直线都相交的两条直线一定是异面直线;
②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;
③垂直于同一直线的两条直线相互平行;
④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.
其中,为真命题的是
A. ①和② B. ②和③ C. ③和④ D. ②和④
6.若不等式对于一切非零实数x均成立,则实数的取值范围是
A. [-1,1] B. C. (-2,2) D.[-2,2]
7.如图,已知双曲线, 分别是虚轴的上、下顶点,是左顶点,为左焦点,直线与相交于点,则的余弦值是
A. B. C. D.
8.定义方程的实数根x0叫做函数的“新驻点”,如果函数, ,()的“新驻点”分别为,,,那么,,的大小关系是:
A. B. C. D.
二、填空题:本大题共8小题,考生作答7小题,每小题5分,满分35分.
(一)必做题(9~13题)
9.设集合A={4,5,7,9},B={3,4,7,8,9},全集U=AB,则集合= 。
10.的展开式中的常数项是: 。(请用数字作答)
11.已知平面区域,,若在区域上随机投一点P,则点P落在区域M的概率为: 。
12.已知△ABC三边长分别为1、2、a,“△ABC为锐角三角形”的充要条件是:“ ”。
13.有以下命题:设是公差为d的等差数列中任意m项,若,则;特别地,当r=0时,称为的等差平均项。
⑴已知等差数列的通项公式为=2n,根据上述命题,则的等差平均项为: ;
⑵将上述真命题推广到各项为正实数的等比数列中:设是公比为q的等比数列中任意m项,若,则 ;特别地,当r=0时,称为的等比平均项。
(二)选做题(14~16题,考生只能从中选做两题)
14.(优选法选做题)那霉素发酵液生物测定,一般都规定培养温度为()0C,培养时间在16小时以上,某制药厂为了缩短时间,决定优选培养温度,试验范围固定在29~500C,精确度要求,用分数法安排实验,令第一试点在处,第二试点在处,则 =
0C。
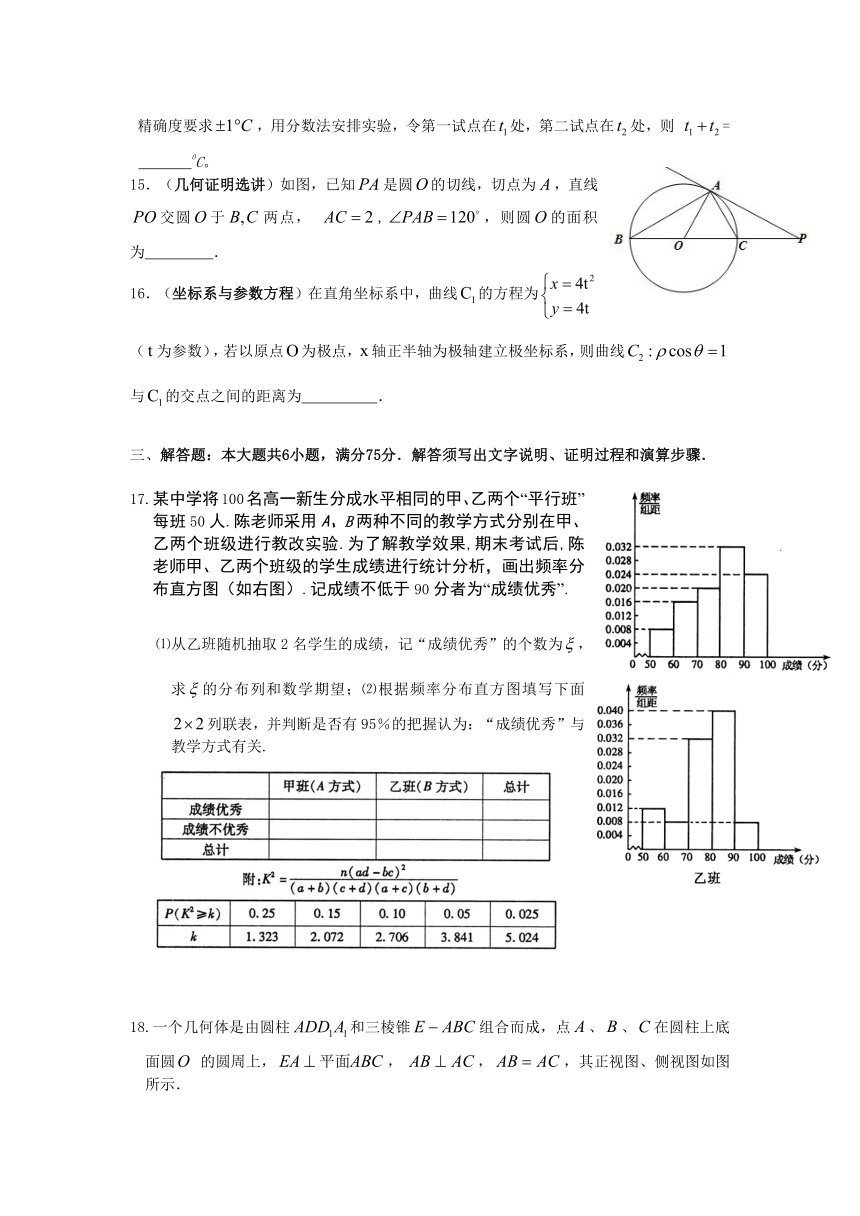
15.(几何证明选讲)如图,已知是圆的切线,切点为,直线交圆于两点, ,,则圆的面积为 .
16.(坐标系与参数方程)在直角坐标系中,曲线的方程为(为参数),若以原点为极点,轴正半轴为极轴建立极坐标系,则曲线与的交点之间的距离为 .
三、解答题:本大题共6小题,满分75分.解答须写出文字说明、证明过程和演算步骤.
17.某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A、B两种不同的教学方式分别在甲、乙两个班级进行教改实验.为了解教学效果,期末考试后,陈老师甲、乙两个班级的学生成绩进行统计分析,画出频率分布直方图(如右图).记成绩不低于90分者为“成绩优秀”.
⑴从乙班随机抽取2名学生的成绩,记“成绩优秀”的个数为,求的分布列和数学期望;⑵根据频率分布直方图填写下面列联表,并判断是否有95%的把握认为:“成绩优秀”与教学方式有关.
18.一个几何体是由圆柱和三棱锥组合而成,点、、在圆柱上底面圆 的圆周上,,,,其正视图、侧视图如图所示.
⑴求证:;
⑵求锐二面角的大小.
19.已知椭圆的离心率. 直线()与曲线交于
不同的两点,以线段为直径作圆,圆心为.
⑴求椭圆的方程;
⑵若圆与轴相交于不同的两点,且的面积为,求圆的标准方程.
20.世界大学生运动会圣火台如图所示,圣火盆是半径为1m的圆,并 通过三根长度相等的金属支架、、(、、是圆上的三等分点)将其水平放置,另一根金属支架垂直于地面,已知圣火盘的圆心到地面的距离为m,四根金属支架的总长度为ym.
⑴设,请写出y关于的函数解析式,并写出函数的定义域;
⑵试确定点的位置,使四根金属支架的总长度最短.(参考数值:,其中)
21. 定义:若数列满足,则称数列为“平方数列”。已知数列 中,,点在函数的图像上,其中为正整数。
⑴证明:数列是“平方数列”,且数列为等比数列。
⑵设⑴中“平方数列”的前项之积为,即,求数列的通项及关于的表达式。
⑶记,求数列的前项之和,并求使的的最小值。
22. 已知函数的图象在点(为自然对数的底数)处的切线斜率为3.
⑴求实数的值;
⑵若,且对任意恒成立,求的最大值;
⑶当时,证明.
参考答案
一、选择题:
D B A C D B C D
二、填空题:本大题共8小题,考生作答7小题,每小题5分,满分35分.
(一)必做题(9~13题)
9.{3,5,8}
10.-20
11.
12.
13. 16;
(二)选做题(14~16题,考生只能从中选做两题)
14. 79
15.
16.
三、解答题:本大题共6小题,满分75分.解答须写出文字说明、证明过程和演算步骤.
17.
18.方法1:(1)证明:因为,,所以,即.
又因为,,所以平面.
因为,所以.………………………………………5分
(2)解: ,.
过点作于点,连接,
由(1)知,,,所以平面.
因为平面,所以.
所以为二面角的平面角.
由(1)知,平面,平面,
所以,即△为直角三角形.
在△中,,,则.
由,解得.
因为.
所以.
所以二面角的平面角大小为.
方法2:(2)解:设是平面的法向量,因为,
所以即
取,则是平面的一个法向量.
由(1)知,,又,,所以平面.
所以是平面的一个法向量.
因为,
所以.
而等于二面角的平面角,
所以二面角的平面角大小为.……………………………………12分
19.解:(1)∵椭圆的离心率, ∴ . 解得.
∴ 椭圆的方程为.
(2)依题意,圆心为.
由 得. ∴ 圆的半径为.
∵ 圆与轴相交于不同的两点,且圆心到轴的距离,
∴ ,即.
∴ 弦长.
∴的面积.
∴ 圆的标准方程为.
20.
21. (Ⅰ)由条件an+1=2an2+2an, 得2an+1+1=4an2+4an+1=(2an+1)2.∴{bn}是“平方数列”.
∴lgbn+1=2lgbn.∵lg(2a1+1)=lg5≠0,∴=2.∴{lg(2an+1)}为等比数列.
(Ⅱ)∵lg(2a1+1)=lg5,∴lg(2an+1)=2n-1lg5,∴2an+1=5,∴an=(5-1).
∵lgTn=lg(2a1+1)+lg(2a2+1)+…+lg(2an+1)==(2n-1)lg5.
∴Tn=5.
(3)cn====2- eq \b\bc\(() eq \s\up10(n-1),
∴Sn=2n-[1++ eq \b\bc\(() eq \s\up10(2)+…+ eq \b\bc\(() eq \s\up10(n-1)]=2n- eq \f(1- eq \b\bc\(() eq \s\up10(n),1-)=2n-2[1- eq \b\bc\(() eq \s\up10(n)]=2n-2+2 eq \b\bc\(() eq \s\up10(n).
由Sn>4020得2n-2+2 eq \b\bc\(() eq \s\up10(n)>4020,n+ eq \b\bc\(() eq \s\up10(n)>2011,
当n≤2010时,n+ eq \b\bc\(() eq \s\up10(n)<2011,当n≥2011时,n+ eq \b\bc\(() eq \s\up10(n)>2011,∴n的最小值为2011.
22.(1)解:因为,所以.
因为函数的图像在点处的切线斜率为3,
所以,即.
所以.
(2)解:由(1)知,,
所以对任意恒成立,即对任意恒成立.
令,
则,
令,
则,
所以函数在上单调递增.
因为,
所以方程在上存在唯一实根,且满足.
当,即,当,即,
所以函数在上单调递减,在上单调递增.
所以
.
所以.
故整数的最大值是3.
(3)证明1:由(2)知,是上的增函数,
所以当时,.
即.
整理,得
.
因为, 所以.
即.
即.
所以.
证明2:构造函数
,
则.
因为,所以.
所以函数在上单调递增.
因为, 所以.
所以
.
即.
即.
即.
所以
A
D11
A11
E
B
C
O
D
A
D11
A11
E
B
C
O
D
x
y
z
数 学
(试卷满分:150分 考试试卷:120分钟)
一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.函数图像的对称轴方程可以是
A. B. C. D.
2.设实数且(其中是虚数单位)为正实数,则的值为
A.-1 B.0 C.0或-1 D.1
3.已知向量、满足且则=
A.10 B.20 C.21 D.30
4.已知,由如右程序框图输出的
A. 0 B. C. 1 D.
5.给定下列四个命题:
①分别与两条异面直线都相交的两条直线一定是异面直线;
②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;
③垂直于同一直线的两条直线相互平行;
④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.
其中,为真命题的是
A. ①和② B. ②和③ C. ③和④ D. ②和④
6.若不等式对于一切非零实数x均成立,则实数的取值范围是
A. [-1,1] B. C. (-2,2) D.[-2,2]
7.如图,已知双曲线, 分别是虚轴的上、下顶点,是左顶点,为左焦点,直线与相交于点,则的余弦值是
A. B. C. D.
8.定义方程的实数根x0叫做函数的“新驻点”,如果函数, ,()的“新驻点”分别为,,,那么,,的大小关系是:
A. B. C. D.
二、填空题:本大题共8小题,考生作答7小题,每小题5分,满分35分.
(一)必做题(9~13题)
9.设集合A={4,5,7,9},B={3,4,7,8,9},全集U=AB,则集合= 。
10.的展开式中的常数项是: 。(请用数字作答)
11.已知平面区域,,若在区域上随机投一点P,则点P落在区域M的概率为: 。
12.已知△ABC三边长分别为1、2、a,“△ABC为锐角三角形”的充要条件是:“ ”。
13.有以下命题:设是公差为d的等差数列中任意m项,若,则;特别地,当r=0时,称为的等差平均项。
⑴已知等差数列的通项公式为=2n,根据上述命题,则的等差平均项为: ;
⑵将上述真命题推广到各项为正实数的等比数列中:设是公比为q的等比数列中任意m项,若,则 ;特别地,当r=0时,称为的等比平均项。
(二)选做题(14~16题,考生只能从中选做两题)
14.(优选法选做题)那霉素发酵液生物测定,一般都规定培养温度为()0C,培养时间在16小时以上,某制药厂为了缩短时间,决定优选培养温度,试验范围固定在29~500C,精确度要求,用分数法安排实验,令第一试点在处,第二试点在处,则 =
0C。
15.(几何证明选讲)如图,已知是圆的切线,切点为,直线交圆于两点, ,,则圆的面积为 .
16.(坐标系与参数方程)在直角坐标系中,曲线的方程为(为参数),若以原点为极点,轴正半轴为极轴建立极坐标系,则曲线与的交点之间的距离为 .
三、解答题:本大题共6小题,满分75分.解答须写出文字说明、证明过程和演算步骤.
17.某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A、B两种不同的教学方式分别在甲、乙两个班级进行教改实验.为了解教学效果,期末考试后,陈老师甲、乙两个班级的学生成绩进行统计分析,画出频率分布直方图(如右图).记成绩不低于90分者为“成绩优秀”.
⑴从乙班随机抽取2名学生的成绩,记“成绩优秀”的个数为,求的分布列和数学期望;⑵根据频率分布直方图填写下面列联表,并判断是否有95%的把握认为:“成绩优秀”与教学方式有关.
18.一个几何体是由圆柱和三棱锥组合而成,点、、在圆柱上底面圆 的圆周上,,,,其正视图、侧视图如图所示.
⑴求证:;
⑵求锐二面角的大小.
19.已知椭圆的离心率. 直线()与曲线交于
不同的两点,以线段为直径作圆,圆心为.
⑴求椭圆的方程;
⑵若圆与轴相交于不同的两点,且的面积为,求圆的标准方程.
20.世界大学生运动会圣火台如图所示,圣火盆是半径为1m的圆,并 通过三根长度相等的金属支架、、(、、是圆上的三等分点)将其水平放置,另一根金属支架垂直于地面,已知圣火盘的圆心到地面的距离为m,四根金属支架的总长度为ym.
⑴设,请写出y关于的函数解析式,并写出函数的定义域;
⑵试确定点的位置,使四根金属支架的总长度最短.(参考数值:,其中)
21. 定义:若数列满足,则称数列为“平方数列”。已知数列 中,,点在函数的图像上,其中为正整数。
⑴证明:数列是“平方数列”,且数列为等比数列。
⑵设⑴中“平方数列”的前项之积为,即,求数列的通项及关于的表达式。
⑶记,求数列的前项之和,并求使的的最小值。
22. 已知函数的图象在点(为自然对数的底数)处的切线斜率为3.
⑴求实数的值;
⑵若,且对任意恒成立,求的最大值;
⑶当时,证明.
参考答案
一、选择题:
D B A C D B C D
二、填空题:本大题共8小题,考生作答7小题,每小题5分,满分35分.
(一)必做题(9~13题)
9.{3,5,8}
10.-20
11.
12.
13. 16;
(二)选做题(14~16题,考生只能从中选做两题)
14. 79
15.
16.
三、解答题:本大题共6小题,满分75分.解答须写出文字说明、证明过程和演算步骤.
17.
18.方法1:(1)证明:因为,,所以,即.
又因为,,所以平面.
因为,所以.………………………………………5分
(2)解: ,.
过点作于点,连接,
由(1)知,,,所以平面.
因为平面,所以.
所以为二面角的平面角.
由(1)知,平面,平面,
所以,即△为直角三角形.
在△中,,,则.
由,解得.
因为.
所以.
所以二面角的平面角大小为.
方法2:(2)解:设是平面的法向量,因为,
所以即
取,则是平面的一个法向量.
由(1)知,,又,,所以平面.
所以是平面的一个法向量.
因为,
所以.
而等于二面角的平面角,
所以二面角的平面角大小为.……………………………………12分
19.解:(1)∵椭圆的离心率, ∴ . 解得.
∴ 椭圆的方程为.
(2)依题意,圆心为.
由 得. ∴ 圆的半径为.
∵ 圆与轴相交于不同的两点,且圆心到轴的距离,
∴ ,即.
∴ 弦长.
∴的面积.
∴ 圆的标准方程为.
20.
21. (Ⅰ)由条件an+1=2an2+2an, 得2an+1+1=4an2+4an+1=(2an+1)2.∴{bn}是“平方数列”.
∴lgbn+1=2lgbn.∵lg(2a1+1)=lg5≠0,∴=2.∴{lg(2an+1)}为等比数列.
(Ⅱ)∵lg(2a1+1)=lg5,∴lg(2an+1)=2n-1lg5,∴2an+1=5,∴an=(5-1).
∵lgTn=lg(2a1+1)+lg(2a2+1)+…+lg(2an+1)==(2n-1)lg5.
∴Tn=5.
(3)cn====2- eq \b\bc\(() eq \s\up10(n-1),
∴Sn=2n-[1++ eq \b\bc\(() eq \s\up10(2)+…+ eq \b\bc\(() eq \s\up10(n-1)]=2n- eq \f(1- eq \b\bc\(() eq \s\up10(n),1-)=2n-2[1- eq \b\bc\(() eq \s\up10(n)]=2n-2+2 eq \b\bc\(() eq \s\up10(n).
由Sn>4020得2n-2+2 eq \b\bc\(() eq \s\up10(n)>4020,n+ eq \b\bc\(() eq \s\up10(n)>2011,
当n≤2010时,n+ eq \b\bc\(() eq \s\up10(n)<2011,当n≥2011时,n+ eq \b\bc\(() eq \s\up10(n)>2011,∴n的最小值为2011.
22.(1)解:因为,所以.
因为函数的图像在点处的切线斜率为3,
所以,即.
所以.
(2)解:由(1)知,,
所以对任意恒成立,即对任意恒成立.
令,
则,
令,
则,
所以函数在上单调递增.
因为,
所以方程在上存在唯一实根,且满足.
当,即,当,即,
所以函数在上单调递减,在上单调递增.
所以
.
所以.
故整数的最大值是3.
(3)证明1:由(2)知,是上的增函数,
所以当时,.
即.
整理,得
.
因为, 所以.
即.
即.
所以.
证明2:构造函数
,
则.
因为,所以.
所以函数在上单调递增.
因为, 所以.
所以
.
即.
即.
即.
所以
A
D11
A11
E
B
C
O
D
A
D11
A11
E
B
C
O
D
x
y
z
同课章节目录
