16.2线段的垂直平分线课件
图片预览


文档简介
(共14张PPT)
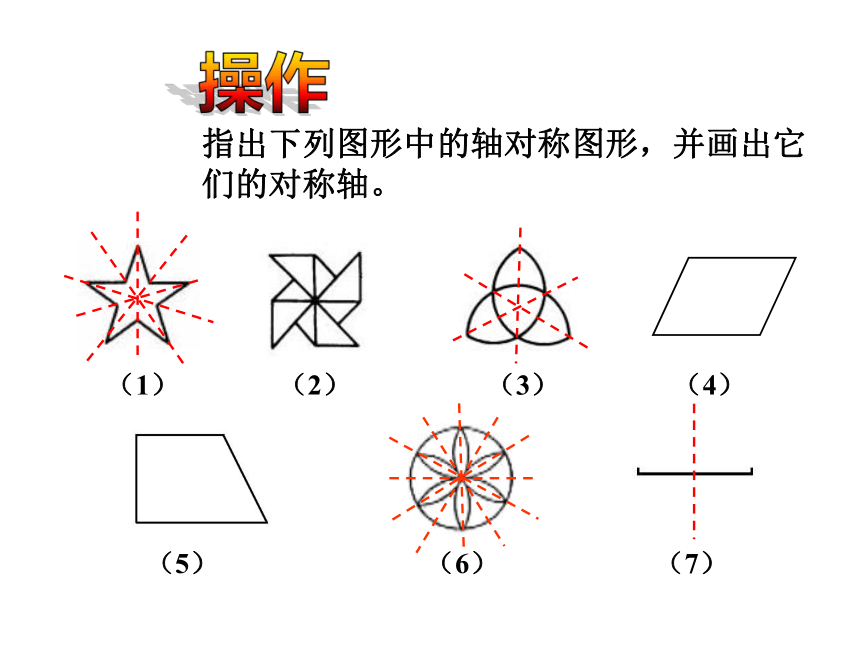
指出下列图形中的轴对称图形,并画出它们的对称轴。
(1) (2) (3) (4)
(5) (6) (7)
怎样做出一条线段的垂直平分线?
2. 过点E、F作直线。
1. 分别以点A、B为圆心,大于
长为半径,画弧
交于点E、F;
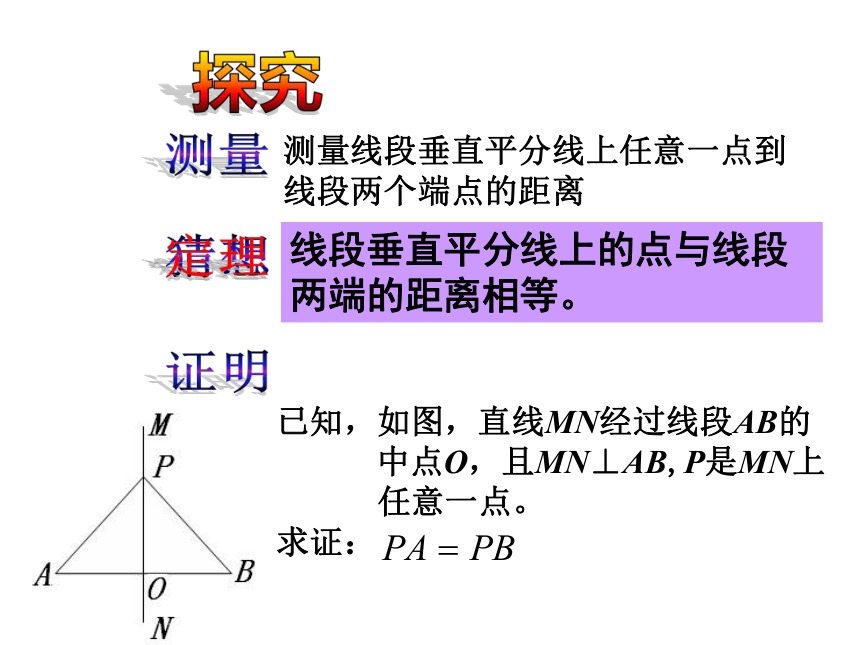
测量线段垂直平分线上任意一点到线段两个端点的距离
已知,如图,直线MN经过线段AB的
中点O,且MN⊥AB,P是MN上
任意一点。
求证:
线段垂直平分线上的点与线段两端的距离相等。
线段垂直平分线上的点与线段两端的距离相等。
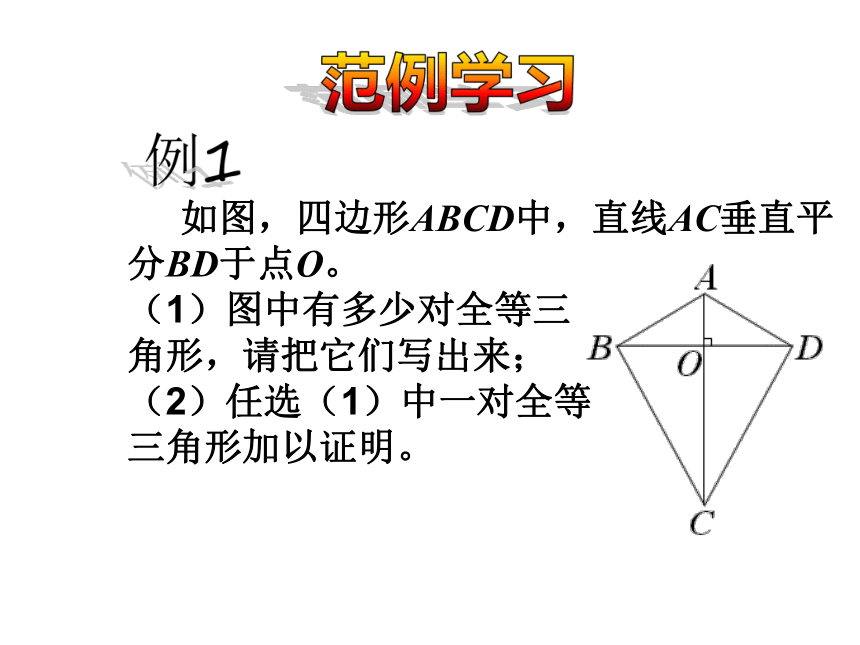
如图,四边形ABCD中,直线AC垂直平分BD于点O。
(1)图中有多少对全等三 角形,请把它们写出来;
(2)任选(1)中一对全等 三角形加以证明。
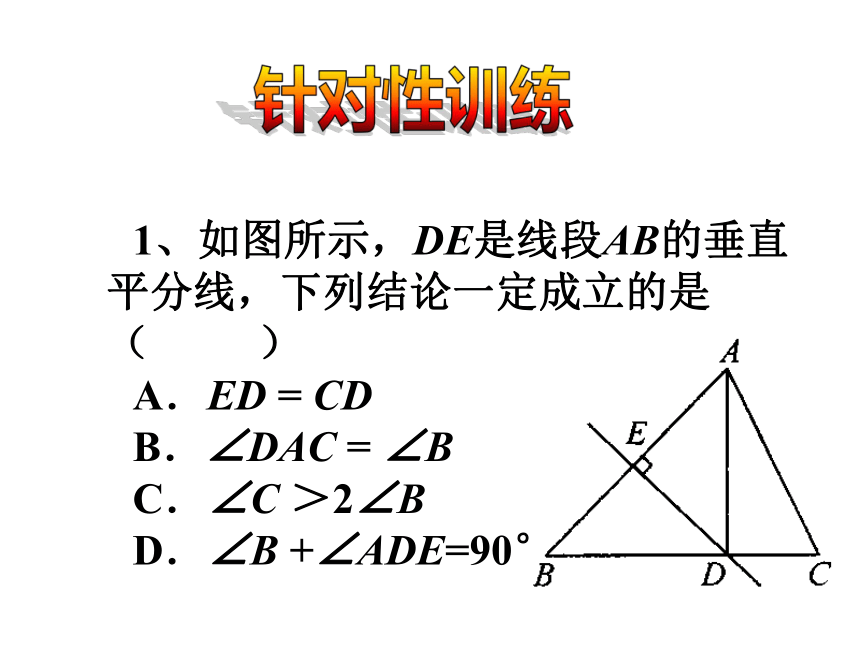
1、如图所示,DE是线段AB的垂直平分线,下列结论一定成立的是( )
A.ED = CD
B.∠DAC = ∠B
C.∠C >2∠B
D.∠B +∠ADE=90°
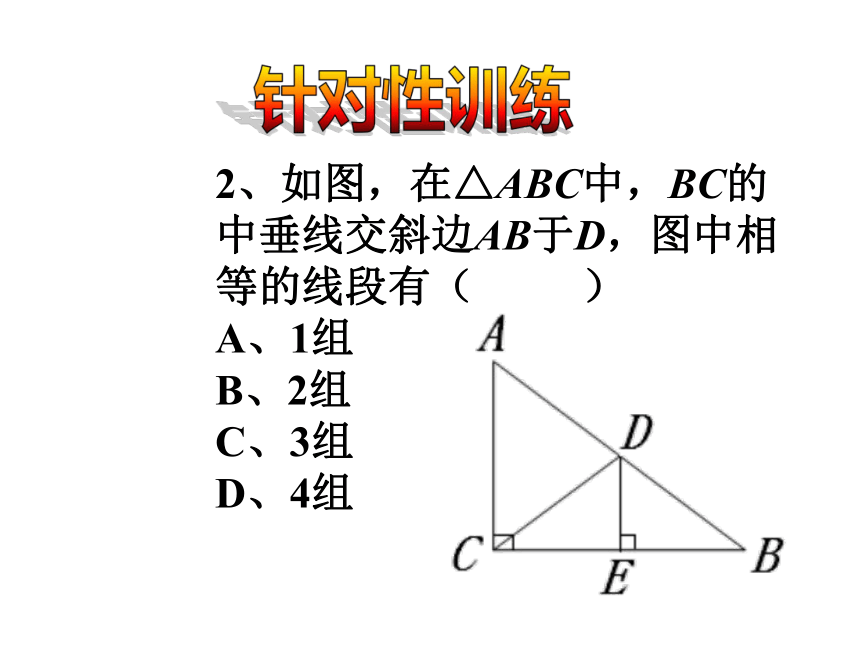
2、如图,在△ABC中,BC的中垂线交斜边AB于D,图中相等的线段有( )
A、1组
B、2组
C、3组
D、4组
3、已知,如图,y轴垂直平分线段BC,点A在y轴上,点B、C在x轴上。
(1)若点C的坐标为(3,0),则点B的坐标是__________;
(2)若点B的坐标为(m,0),则点C的坐标是___________。
4、已知如图,DE是△ABC的边AB的垂直平分线,D为垂足,DE交AC于点E,且AC=8,BC=5,则△BEC的周长为_____________。
5、公路l同侧的A、B两村,共同出资在公路边修建一个停靠站C,使停靠站到A、B两村距离相等,你如何确定停靠站C的位置。
你能写出上述定理的逆命题吗?它是真命题吗?
与线段两端距离相等的点在这条线段的垂直平分线上。
与线段两端距离相等的点在这条线段的垂直平分线上。
线段垂直平分线上的点与线段两端的距离相等。
已知:如图,DE、DF分别是△ABD
和△ACD的高,DE=DF。
求证:AD垂直平分EF。
一个方法
证明线段相等的新方法:利用线段垂直平分线的性质。
两条定理
线段垂直平分线上的点与线段两端的距离相等。
与线段两端距离相等的点在这条线段的垂直平分线上。
三种作图
折纸; 过中点做垂线; 尺规作图法
1、必做作业:
(1)课本:P 124 习题16.2 第3、4题
(2)《基础训练》 16.2 同步练习1
2、选做作业:青岛国际帆船中心要修建一处公共服务设施,使它到三所运动员公寓A、B、C的距离相等。
(1)若三所运动员公寓A、B、C的
位置如图所示,请在图中确定
这处公共服务设施P的位置;
(2)若∠BAC=66°,
则∠BAC= _____;
(3)若∠BAC=α,
则∠BAC= _____.
指出下列图形中的轴对称图形,并画出它们的对称轴。
(1) (2) (3) (4)
(5) (6) (7)
怎样做出一条线段的垂直平分线?
2. 过点E、F作直线。
1. 分别以点A、B为圆心,大于
长为半径,画弧
交于点E、F;
测量线段垂直平分线上任意一点到线段两个端点的距离
已知,如图,直线MN经过线段AB的
中点O,且MN⊥AB,P是MN上
任意一点。
求证:
线段垂直平分线上的点与线段两端的距离相等。
线段垂直平分线上的点与线段两端的距离相等。
如图,四边形ABCD中,直线AC垂直平分BD于点O。
(1)图中有多少对全等三 角形,请把它们写出来;
(2)任选(1)中一对全等 三角形加以证明。
1、如图所示,DE是线段AB的垂直平分线,下列结论一定成立的是( )
A.ED = CD
B.∠DAC = ∠B
C.∠C >2∠B
D.∠B +∠ADE=90°
2、如图,在△ABC中,BC的中垂线交斜边AB于D,图中相等的线段有( )
A、1组
B、2组
C、3组
D、4组
3、已知,如图,y轴垂直平分线段BC,点A在y轴上,点B、C在x轴上。
(1)若点C的坐标为(3,0),则点B的坐标是__________;
(2)若点B的坐标为(m,0),则点C的坐标是___________。
4、已知如图,DE是△ABC的边AB的垂直平分线,D为垂足,DE交AC于点E,且AC=8,BC=5,则△BEC的周长为_____________。
5、公路l同侧的A、B两村,共同出资在公路边修建一个停靠站C,使停靠站到A、B两村距离相等,你如何确定停靠站C的位置。
你能写出上述定理的逆命题吗?它是真命题吗?
与线段两端距离相等的点在这条线段的垂直平分线上。
与线段两端距离相等的点在这条线段的垂直平分线上。
线段垂直平分线上的点与线段两端的距离相等。
已知:如图,DE、DF分别是△ABD
和△ACD的高,DE=DF。
求证:AD垂直平分EF。
一个方法
证明线段相等的新方法:利用线段垂直平分线的性质。
两条定理
线段垂直平分线上的点与线段两端的距离相等。
与线段两端距离相等的点在这条线段的垂直平分线上。
三种作图
折纸; 过中点做垂线; 尺规作图法
1、必做作业:
(1)课本:P 124 习题16.2 第3、4题
(2)《基础训练》 16.2 同步练习1
2、选做作业:青岛国际帆船中心要修建一处公共服务设施,使它到三所运动员公寓A、B、C的距离相等。
(1)若三所运动员公寓A、B、C的
位置如图所示,请在图中确定
这处公共服务设施P的位置;
(2)若∠BAC=66°,
则∠BAC= _____;
(3)若∠BAC=α,
则∠BAC= _____.
