高中数学人教A版选修1-2课件:2.1.2 演绎推理课件(共33张PPT)
文档属性
| 名称 | 高中数学人教A版选修1-2课件:2.1.2 演绎推理课件(共33张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-25 12:34:50 | ||
图片预览









文档简介
(共33张PPT)
第二章
推理与证明
2.1.2
演绎推理
1、什么是演绎推理?
2、什么是三段论?
3、合情推理与演绎推理有哪些区别?
4、能举出一些在生活和学习中有关演绎
推理的例子。
内容:
应用:
1、计算
2、用三段论的形式写出演绎推理
3、证明
本课主要学习演绎推理.从小故事出发,调动学生学习的积极性,让学生初步感受演绎推理的过程;重点是了解演绎推理的含义,能利用“三段论”进行简单的推理.难点是掌握演绎推理的基本方法.另外,从问题入手,引导学生思考探究,在得到演绎推理相关概念的同时又与合情推理做了对比,这样学生的理解和记忆将会更深刻,既突出了重点又突破了难点.
为了巩固新知识,探究了3个例题,例题设置难易适度,每个例题后有针对性的变式训练,便于学生巩固和掌握.另外题型涉及到用演绎推理的概念、一般模式去求解问题,培养学生分析问题和解决问题的能力。通过设置难易不同的必做和选做作业,对不同的学生进行因材施教。
歌德是18世纪德国的一位著名的文艺大师.有一位与其文艺思想相左的文艺批评家,生性古怪,态度傲慢.—天,歌德与他“狭路相逢”,不期而遇.这位文艺批评家见歌德迎面走来,不仅没有有礼貌地打招呼,反而目中无人,高傲地往前直走,并卖弄聪明地大声说:“我从来不给傻子让路!”面对这十分尴尬的情景,歌德镇定自若、笑容可掬,谦恭地闪避一旁,并机智而礼貌地答道:“呵呵,我可恰恰相反.”故作聪明的文艺批评家顿时怔然,讨了个没趣,只得默然离去.
在这故事里,无论是文艺批评家还是歌德,各自都只说了一句,而且话语非常简练,极为深刻,话中有理,语中有刺.他们的对话,体现了演绎推理的三段论法.
(一)复习回顾:合情推理
.归纳推理是由特殊到一般的推理;类比推理是由特殊到特殊的推理.
.一般过程:从具体问题出发
观察、分析、比较、联想
归纳、类比
提出猜想.
.合情推理的结论不一定成立.
合情推理
归纳推理和类比推理都是根据已有的事实,经过观察、分析、比较、联想,再进行归纳、类比,然后提出猜想的推理,我们把它们统称为合情推理。
通俗地说,合情推理是指“合乎情理”的推理。
合情推理的应用
数学研究中,得到一个新结论之前,合情推理常常能帮助我们猜测和发现结论。
证明一个数学结论之前,合情推理常常能为我们提供证明的思路和方向
1.所有的金属都能导电,
2.一切奇数都不能被2整除,
3.三角函数都是周期函数,
4.全等的三角形面积相等
所以铜能够导电.
因为铜是金属,
所以(2100+1)不能被2整除.
因为(2100+1)是奇数,
所以是tan
周期函数
因为tan
三角函数,
那么三角形ABC与三角形A1B1C1面积相等.
如果三角形ABC与三角形A1B1C1全等,
大前提
小前提
结论
大前提
小前提
结论
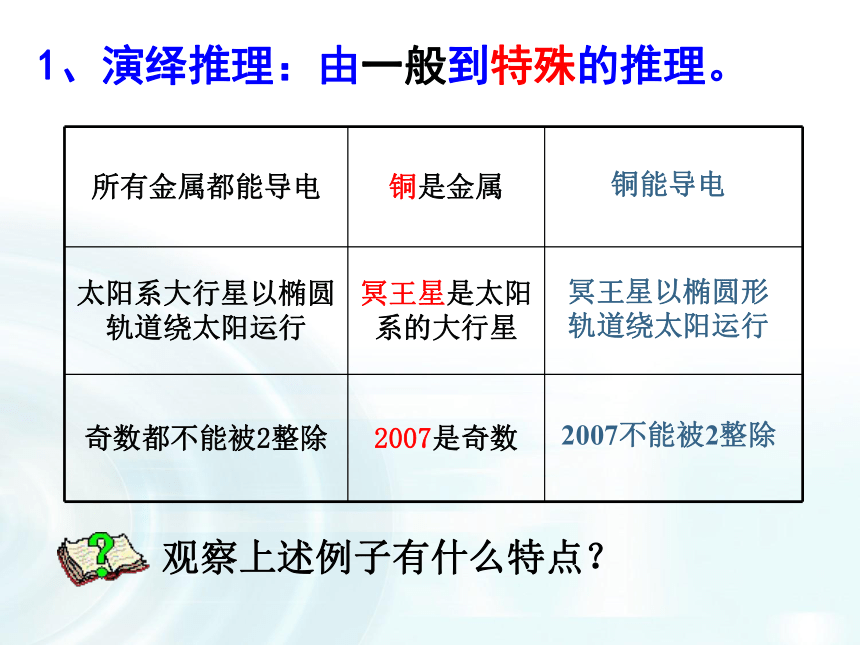
观察上述例子有什么特点?
1、演绎推理:由一般到特殊的推理。
所有金属都能导电
铜是金属
太阳系大行星以椭圆轨道绕太阳运行
冥王星是太阳系的大行星
奇数都不能被2整除
2007是奇数
2007不能被2整除
冥王星以椭圆形轨道绕太阳运行
铜能导电
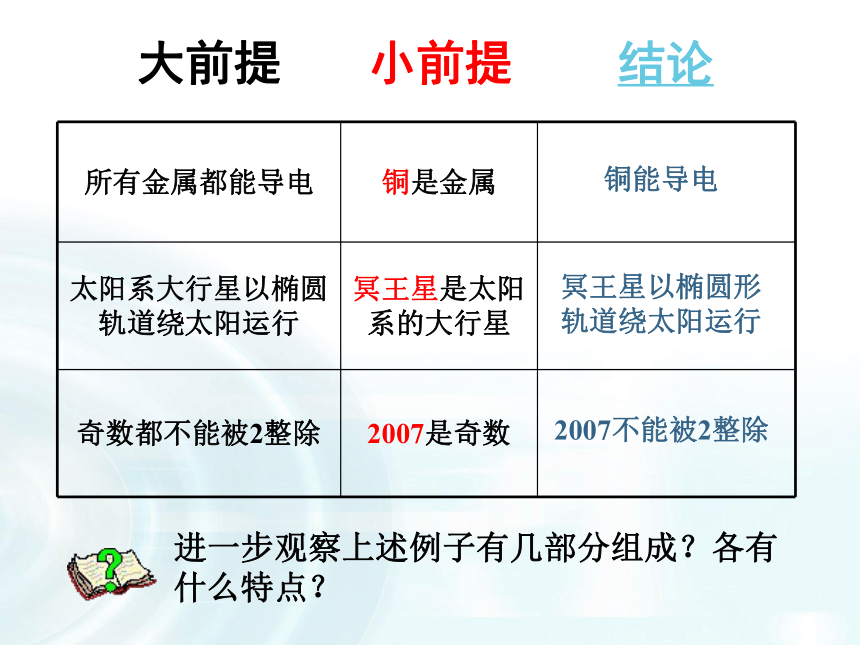
进一步观察上述例子有几部分组成?各有什么特点?
大前提
小前提
结论
所有金属都能导电
铜是金属
太阳系大行星以椭圆轨道绕太阳运行
冥王星是太阳系的大行星
奇数都不能被2整除
2007是奇数
2007不能被2整除
冥王星以椭圆形轨道绕太阳运行
铜能导电
从一般性的原理出发,推出某个特殊情况下的结论,这种推理称为演绎推理.
演绎推理的定义:
演绎推理的模式:
“三段论”是演绎推理的一般模式;
M……P(M是P)
S……M
(S是M)
S……P
(S是P)
大前提---已知的一般原理;
小前提---所研究的特殊对象;
结论---据一般原理,对特殊
对象做出的判断.
M
S
P
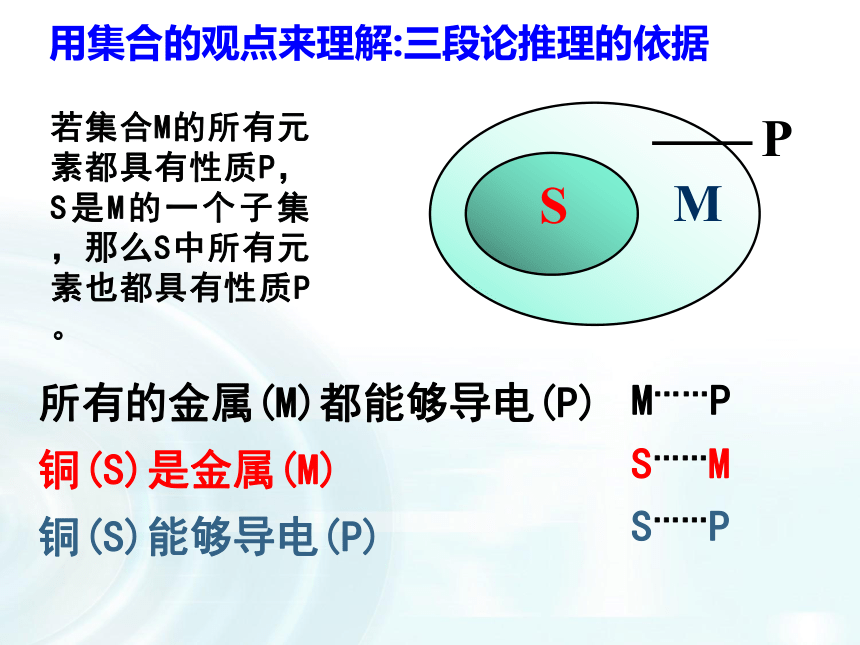
若集合M的所有元素都具有性质P,S是M的一个子集,那么S中所有元素也都具有性质P。
所有的金属(M)都能够导电(P)
铜(S)是金属(M)
铜(S)能够导电(P)
M……P
S……M
S……P
用集合的观点来理解:三段论推理的依据
(1)因为指数函数
是增函数,
而
是指数函数,
所以
是增函数。
错因:大前提是错误的,所以结论是错误的。
演绎推理的结论一定正确吗?
(2)如图:在△ABC中,AC>BC,CD是AB边上的高,求证∠ACD>∠BCD。
A
C
D
B
证明:
在△ABC中,
因为CD⊥AB,AC>BC
所以AD>BD,
于是∠ACD>∠
BCD。
错因:偷换概念
(3)因为金属铜、铁、铝能够导电(大前提),而金是金属(小前提),所以金能导电(结论)
错因:推理形式错误。
因为演绎推理是从一般到特殊的推理,铜、铁、铝
是特殊事例,从特殊到特殊的推理不是演绎推理。
所有金属都能导电
铜是金属
太阳系大行星以椭
圆轨道绕太阳运行
冥王星是太阳系的大行星
奇数都不能被2整除
2007是奇数
2007不能被2整除
冥王星以椭圆形轨道绕太阳运行
铜能导电
大前提
小前提
结论
(3)
在演绎推理中,只要前提和推理形式是正确的,结论必定正确。
大前提:刑法规定抢劫罪是以非法占有为目的,使用暴力、胁迫或其他方法,强行劫取公私财物的行为。其刑事责任年龄起点为14周岁,对财物的数额没有要求。
小前提:小明超过14周岁,强行向路人抢取钱财50元。
结论:小明犯了抢劫罪。
小明是一名高二年级的学生,17岁,迷恋上网络,沉迷于虚拟的世界当中。由于每月的零花钱不够用,便向亲戚要钱,但这仍然满足不了需求,于是就产生了歹念,强行向路人抢取钱财。但小明却说我是未成年人而且就抢了50元,这应该不会很严重吧??如果你是法官,你会如何判决呢?
演绎推理的特点:
1.演绎推理的前提是一般性原理,演绎所得的的结论是蕴含于前提之中的个别、特殊事实,结论完全蕴含于前提之中,因此演绎推理是由一般到特殊的推理;
2、在演绎推理中,前提于结论之间存在着必然的联系,只要前提和推理形式是正确的,结论必定正确。因此演绎推理是数学中严格的证明工具。
3、在演绎推理是一种收敛性的思维方法,它较少创造性,但却具有条理清晰、令人信服的论证作用,有助于科学论证和系统化。
合情推理与演绎推理的区别
区别
推理
形式
推理结论
联系
合情推理
归纳推理
类比推理
由部分到整体、个
别到一般的推理。
由特殊到特殊
的推理。
结论不一定正确,有待进一步证明。
演绎推理
由一般到特殊的
推理。
在大前提、小前提
和推理形式都正确
的前提下,得到的
结论一定正确。
合情推理的结论需要演绎推理的验证,而演绎
推理的方向和思路一般是通过合情推理获得的。
推
理
合情推理
(或然性推理)
演绎推理
(必然性推理)
归纳
(特殊到一般)
类比
(特殊到特殊)
三段论
(一般到特殊)
大前提
小前提
结论
大前提
小前提
结论
1、下面说法正确的有(
)
(1)演绎推理是由一般到特殊的推理;
(2)演绎推理得到的结论一定是正确的;
(3)演绎推理一般模式是“三段论”形式;
(4)演绎推理的结论的正误与大前提、小前提和推理形式有关。
A、1个
B、2个
C、3个
D、4个
C
例2:用三段论的形式写出下列演绎推理。
(1)三角形内角和180°,等边三角形内角和180°
(1)分析:省略了小前提:等边三角形是三角形”。
:
是有理数。
(2)分析:省略了大前提:“所有的循环小数都是有理数。”
小前提:
是循环小数。
解(1)三角形内角和180°,(大前提)
所以等边三角形内角和是180°。(结论)
等边三角形是三角形。(小前提)
结论
(2)
是有理数。
2、下列几种推理过程是演绎推理的是(
)
A、5和
可以比较大小;
B、由平面三角形的性质,推测空间四面体的性质;
C、东升高中高二级有15个班,1班有51人,2班有53人,3班有52人,由此推测各班都超过50人;
D、预测股票走势图。
A
例3:证明函数f(x)=-x2+2x在(-∞,1)是增函数。
证明:任取
函数f(x)=-x2+2x在(-∞,1)是增函数。
大前提:增函数的定义;
小前提
结论
例3:证明函数f(x)=-x2+2x在(-∞,1)是增函数。
函数f(x)=-x2+2x在(-∞,1)是增函数。
大前提:在某个区间(a,b)内若
,那么函数y=f(x)在这个区间内单调递增;
小前提
结论
在锐角三角形ABC中,AD⊥BC,
BE⊥AC,D,E是垂足,用演绎推理“三段论”格式证AB的中点M到D,E的距离相等.
A
D
E
C
M
B
(1)因为有一个内角是直角的三角形是直角三角形,
在△ABC中,AD⊥BC,即∠ADB=900
所以△ABD是直角三角形
同理△ABE是直角三角形
大前提
小前提
结论
证明:
(2)因为直角三角形斜边上的中线等于斜边的一半,
M是Rt△ABD斜边AB的中点,DM是斜边上的中线
所以
DM=
AB
同理
EM=
AB
所以
DM
=
EM
大前提
小前提
结论
演绎推理概念;
1、
2
、
合情推理与演绎推理的区别与联系.
演绎推理是证明数学结论、建立数学体系的重要思维过程.但数学结论、证明思路等的发现,主要靠合情推理.因此,我们不仅要学会证明,也要学会猜想.
4、
演绎推理的一般模式——三段论.
3、演绎推理错误的主要原因是:
①大前提不成立;②小前提不符合大前提的条件;③推理形式错误.
第二章
推理与证明
2.1.2
演绎推理
1、什么是演绎推理?
2、什么是三段论?
3、合情推理与演绎推理有哪些区别?
4、能举出一些在生活和学习中有关演绎
推理的例子。
内容:
应用:
1、计算
2、用三段论的形式写出演绎推理
3、证明
本课主要学习演绎推理.从小故事出发,调动学生学习的积极性,让学生初步感受演绎推理的过程;重点是了解演绎推理的含义,能利用“三段论”进行简单的推理.难点是掌握演绎推理的基本方法.另外,从问题入手,引导学生思考探究,在得到演绎推理相关概念的同时又与合情推理做了对比,这样学生的理解和记忆将会更深刻,既突出了重点又突破了难点.
为了巩固新知识,探究了3个例题,例题设置难易适度,每个例题后有针对性的变式训练,便于学生巩固和掌握.另外题型涉及到用演绎推理的概念、一般模式去求解问题,培养学生分析问题和解决问题的能力。通过设置难易不同的必做和选做作业,对不同的学生进行因材施教。
歌德是18世纪德国的一位著名的文艺大师.有一位与其文艺思想相左的文艺批评家,生性古怪,态度傲慢.—天,歌德与他“狭路相逢”,不期而遇.这位文艺批评家见歌德迎面走来,不仅没有有礼貌地打招呼,反而目中无人,高傲地往前直走,并卖弄聪明地大声说:“我从来不给傻子让路!”面对这十分尴尬的情景,歌德镇定自若、笑容可掬,谦恭地闪避一旁,并机智而礼貌地答道:“呵呵,我可恰恰相反.”故作聪明的文艺批评家顿时怔然,讨了个没趣,只得默然离去.
在这故事里,无论是文艺批评家还是歌德,各自都只说了一句,而且话语非常简练,极为深刻,话中有理,语中有刺.他们的对话,体现了演绎推理的三段论法.
(一)复习回顾:合情推理
.归纳推理是由特殊到一般的推理;类比推理是由特殊到特殊的推理.
.一般过程:从具体问题出发
观察、分析、比较、联想
归纳、类比
提出猜想.
.合情推理的结论不一定成立.
合情推理
归纳推理和类比推理都是根据已有的事实,经过观察、分析、比较、联想,再进行归纳、类比,然后提出猜想的推理,我们把它们统称为合情推理。
通俗地说,合情推理是指“合乎情理”的推理。
合情推理的应用
数学研究中,得到一个新结论之前,合情推理常常能帮助我们猜测和发现结论。
证明一个数学结论之前,合情推理常常能为我们提供证明的思路和方向
1.所有的金属都能导电,
2.一切奇数都不能被2整除,
3.三角函数都是周期函数,
4.全等的三角形面积相等
所以铜能够导电.
因为铜是金属,
所以(2100+1)不能被2整除.
因为(2100+1)是奇数,
所以是tan
周期函数
因为tan
三角函数,
那么三角形ABC与三角形A1B1C1面积相等.
如果三角形ABC与三角形A1B1C1全等,
大前提
小前提
结论
大前提
小前提
结论
观察上述例子有什么特点?
1、演绎推理:由一般到特殊的推理。
所有金属都能导电
铜是金属
太阳系大行星以椭圆轨道绕太阳运行
冥王星是太阳系的大行星
奇数都不能被2整除
2007是奇数
2007不能被2整除
冥王星以椭圆形轨道绕太阳运行
铜能导电
进一步观察上述例子有几部分组成?各有什么特点?
大前提
小前提
结论
所有金属都能导电
铜是金属
太阳系大行星以椭圆轨道绕太阳运行
冥王星是太阳系的大行星
奇数都不能被2整除
2007是奇数
2007不能被2整除
冥王星以椭圆形轨道绕太阳运行
铜能导电
从一般性的原理出发,推出某个特殊情况下的结论,这种推理称为演绎推理.
演绎推理的定义:
演绎推理的模式:
“三段论”是演绎推理的一般模式;
M……P(M是P)
S……M
(S是M)
S……P
(S是P)
大前提---已知的一般原理;
小前提---所研究的特殊对象;
结论---据一般原理,对特殊
对象做出的判断.
M
S
P
若集合M的所有元素都具有性质P,S是M的一个子集,那么S中所有元素也都具有性质P。
所有的金属(M)都能够导电(P)
铜(S)是金属(M)
铜(S)能够导电(P)
M……P
S……M
S……P
用集合的观点来理解:三段论推理的依据
(1)因为指数函数
是增函数,
而
是指数函数,
所以
是增函数。
错因:大前提是错误的,所以结论是错误的。
演绎推理的结论一定正确吗?
(2)如图:在△ABC中,AC>BC,CD是AB边上的高,求证∠ACD>∠BCD。
A
C
D
B
证明:
在△ABC中,
因为CD⊥AB,AC>BC
所以AD>BD,
于是∠ACD>∠
BCD。
错因:偷换概念
(3)因为金属铜、铁、铝能够导电(大前提),而金是金属(小前提),所以金能导电(结论)
错因:推理形式错误。
因为演绎推理是从一般到特殊的推理,铜、铁、铝
是特殊事例,从特殊到特殊的推理不是演绎推理。
所有金属都能导电
铜是金属
太阳系大行星以椭
圆轨道绕太阳运行
冥王星是太阳系的大行星
奇数都不能被2整除
2007是奇数
2007不能被2整除
冥王星以椭圆形轨道绕太阳运行
铜能导电
大前提
小前提
结论
(3)
在演绎推理中,只要前提和推理形式是正确的,结论必定正确。
大前提:刑法规定抢劫罪是以非法占有为目的,使用暴力、胁迫或其他方法,强行劫取公私财物的行为。其刑事责任年龄起点为14周岁,对财物的数额没有要求。
小前提:小明超过14周岁,强行向路人抢取钱财50元。
结论:小明犯了抢劫罪。
小明是一名高二年级的学生,17岁,迷恋上网络,沉迷于虚拟的世界当中。由于每月的零花钱不够用,便向亲戚要钱,但这仍然满足不了需求,于是就产生了歹念,强行向路人抢取钱财。但小明却说我是未成年人而且就抢了50元,这应该不会很严重吧??如果你是法官,你会如何判决呢?
演绎推理的特点:
1.演绎推理的前提是一般性原理,演绎所得的的结论是蕴含于前提之中的个别、特殊事实,结论完全蕴含于前提之中,因此演绎推理是由一般到特殊的推理;
2、在演绎推理中,前提于结论之间存在着必然的联系,只要前提和推理形式是正确的,结论必定正确。因此演绎推理是数学中严格的证明工具。
3、在演绎推理是一种收敛性的思维方法,它较少创造性,但却具有条理清晰、令人信服的论证作用,有助于科学论证和系统化。
合情推理与演绎推理的区别
区别
推理
形式
推理结论
联系
合情推理
归纳推理
类比推理
由部分到整体、个
别到一般的推理。
由特殊到特殊
的推理。
结论不一定正确,有待进一步证明。
演绎推理
由一般到特殊的
推理。
在大前提、小前提
和推理形式都正确
的前提下,得到的
结论一定正确。
合情推理的结论需要演绎推理的验证,而演绎
推理的方向和思路一般是通过合情推理获得的。
推
理
合情推理
(或然性推理)
演绎推理
(必然性推理)
归纳
(特殊到一般)
类比
(特殊到特殊)
三段论
(一般到特殊)
大前提
小前提
结论
大前提
小前提
结论
1、下面说法正确的有(
)
(1)演绎推理是由一般到特殊的推理;
(2)演绎推理得到的结论一定是正确的;
(3)演绎推理一般模式是“三段论”形式;
(4)演绎推理的结论的正误与大前提、小前提和推理形式有关。
A、1个
B、2个
C、3个
D、4个
C
例2:用三段论的形式写出下列演绎推理。
(1)三角形内角和180°,等边三角形内角和180°
(1)分析:省略了小前提:等边三角形是三角形”。
:
是有理数。
(2)分析:省略了大前提:“所有的循环小数都是有理数。”
小前提:
是循环小数。
解(1)三角形内角和180°,(大前提)
所以等边三角形内角和是180°。(结论)
等边三角形是三角形。(小前提)
结论
(2)
是有理数。
2、下列几种推理过程是演绎推理的是(
)
A、5和
可以比较大小;
B、由平面三角形的性质,推测空间四面体的性质;
C、东升高中高二级有15个班,1班有51人,2班有53人,3班有52人,由此推测各班都超过50人;
D、预测股票走势图。
A
例3:证明函数f(x)=-x2+2x在(-∞,1)是增函数。
证明:任取
函数f(x)=-x2+2x在(-∞,1)是增函数。
大前提:增函数的定义;
小前提
结论
例3:证明函数f(x)=-x2+2x在(-∞,1)是增函数。
函数f(x)=-x2+2x在(-∞,1)是增函数。
大前提:在某个区间(a,b)内若
,那么函数y=f(x)在这个区间内单调递增;
小前提
结论
在锐角三角形ABC中,AD⊥BC,
BE⊥AC,D,E是垂足,用演绎推理“三段论”格式证AB的中点M到D,E的距离相等.
A
D
E
C
M
B
(1)因为有一个内角是直角的三角形是直角三角形,
在△ABC中,AD⊥BC,即∠ADB=900
所以△ABD是直角三角形
同理△ABE是直角三角形
大前提
小前提
结论
证明:
(2)因为直角三角形斜边上的中线等于斜边的一半,
M是Rt△ABD斜边AB的中点,DM是斜边上的中线
所以
DM=
AB
同理
EM=
AB
所以
DM
=
EM
大前提
小前提
结论
演绎推理概念;
1、
2
、
合情推理与演绎推理的区别与联系.
演绎推理是证明数学结论、建立数学体系的重要思维过程.但数学结论、证明思路等的发现,主要靠合情推理.因此,我们不仅要学会证明,也要学会猜想.
4、
演绎推理的一般模式——三段论.
3、演绎推理错误的主要原因是:
①大前提不成立;②小前提不符合大前提的条件;③推理形式错误.
