人教版高中物理必修2第七章第2节功(共35张PPT)
文档属性
| 名称 | 人教版高中物理必修2第七章第2节功(共35张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 996.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-08-25 00:00:00 | ||
图片预览









文档简介
(共35张PPT)
第七章
机械能守恒定律
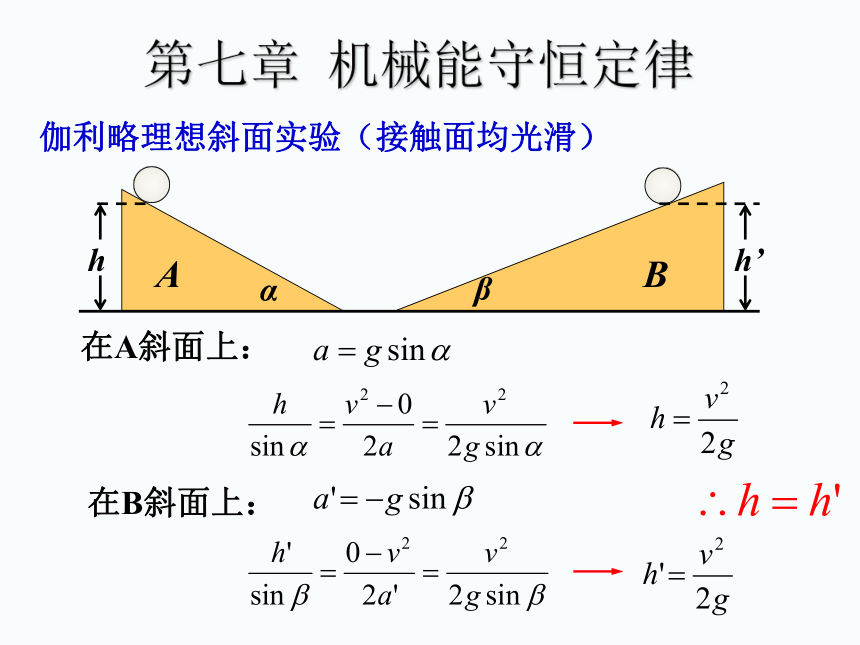
伽利略理想斜面实验(接触面均光滑)
A
B
h
h’
α
β
在A斜面上:
在B斜面上:
相互作用的物体凭借其位置而具有的能量,叫做势能。
物体由于运动而具有的能量,叫做动能。
几种常见的能量形式
重力势能(高度)
弹性势能(形变量)
物质都具有各种形式的能量,各种形式的能量都不是孤立的,不同形式的能量会发生相互转化。
如何量度能量转化了多少?
§7.2
功
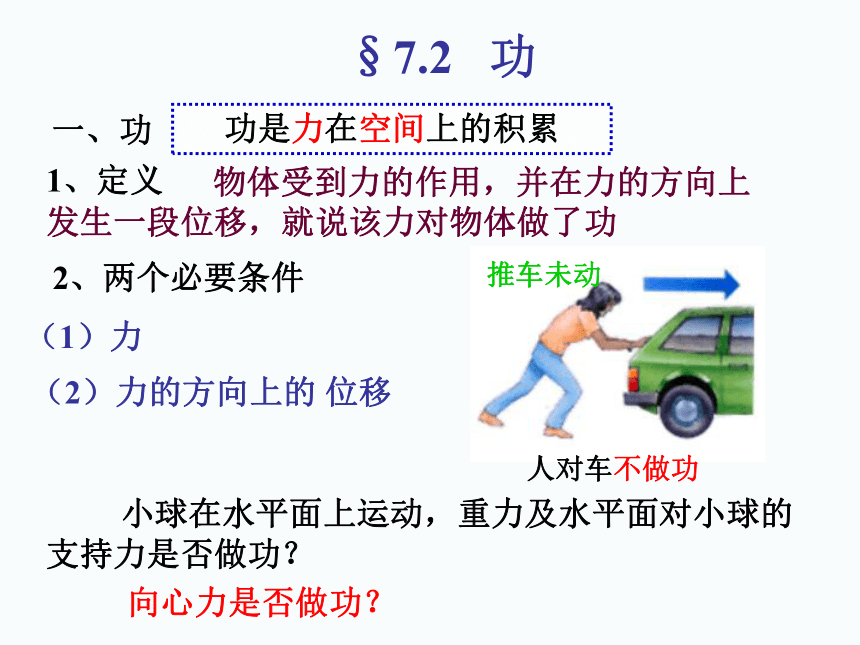
一、功
1、定义
物体受到力的作用,并在力的方向上发生一段位移,就说该力对物体做了功
2、两个必要条件
(1)力
(2)力的方向上的
位移
推车未动
人对车不做功
小球在水平面上运动,重力及水平面对小球的支持力是否做功?
向心力是否做功?
功是力在空间上的积累
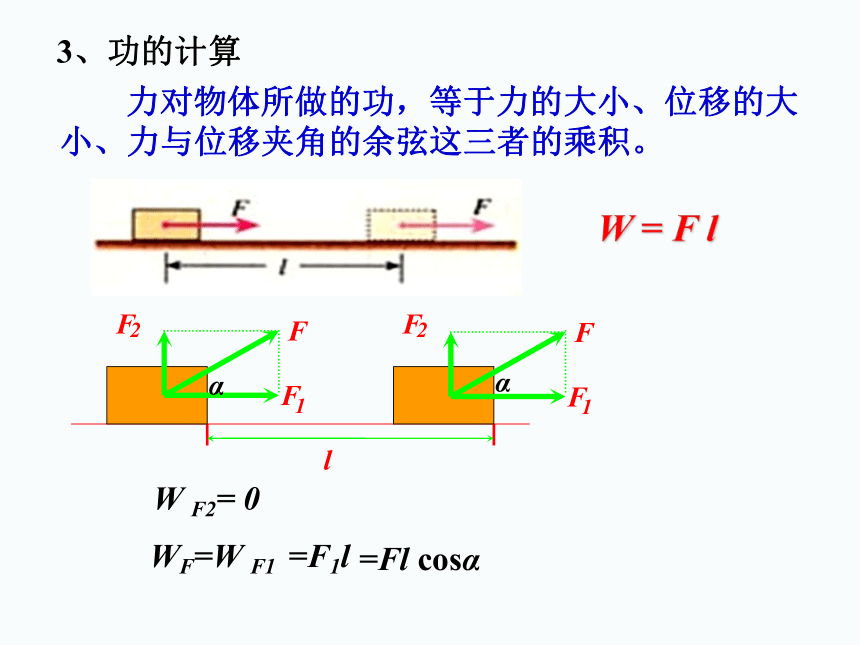
3、功的计算
力对物体所做的功,等于力的大小、位移的大小、力与位移夹角的余弦这三者的乘积。
W
=
F
l
F
2
l
F
F
1
α
F
F
1
F
2
α
W
F2=
0
WF=W
F1
=F1l
=Fl
cosα
W
=
F
l
cosα
公式适用条件:恒力做功
α是
F
与
l
正方向间的夹角
位移
l
为物体的位移,参考系为地面。
功=力乘以力方向的位移
=位移乘以位移方向的力
(2)功的单位:
焦耳(焦、J)
1焦耳=1牛顿·米
意义:1牛的力使物体在力的方向上,通过1米的距离时所做的功为1焦。
(1)公式
例1、两质量相等的物体A、B分别放在粗糙水平面上和光滑的水平面上,在同样的拉力F作用下,产生相同的位移S,则拉力
A、对A做的功多
B、对B做功多
C、一样多
D、以上都有可能
粗糙
光滑
A
B
F
F
θ
θ
C
力对物体做的功只与F、
s、
α三者有关,与物体的运动状态及物体是否还受其他作用力等因素无关。
例2、分别对放在粗糙水平面上的同一物体,施加水平拉力或斜向上的拉力,使物体在这两种情况下的加速度相同,当物体通过相同位移时,这两种情况下拉力的功和合力的功的正确关系是
A.拉力的功和合力的功分别相等
B.拉力的功相等,斜向拉时合力的功大
c.合力的功相等,斜向拉时拉力的功大
D.合力的功相等,斜向拉时拉力的功小
D
4、正功与负功
W
=
F
l
cosα
当α=
0o,W
=
F
l
当α=
90o,W
=
0
当α=
180o,W
=-F
l
当α=
90o,W
=
0,力F不做功
当0≤α<
90o,W
为正值,F对物体做正功
当
90o
<
α≤180o,W
为负值,F对物体做负功,也说,物体克服F做了功
例:滑动摩擦力对物体做功为?10J,
也可以说成物体克服摩擦力做功10J。
功是标量,但有正负,“+”“-”不代表大小。
功的正负只表示动力做功还是阻力做功。
比较功的大小只看绝对值。
例:固定斜面长s,物体质量m,摩擦因数μ,求:物体从斜面顶端滑到底端的过程中各力所做的功。
合力的功=?
5、总功的计算
方法二:分别求出各个外力的功,再把各个外力的功代数相加
方法一:先求出合力,再根据W=F合l
cosα计算功
6、功的物理意义
功是能量转化的量度,是标量
正功代表是动力做功,负功代表阻力做功。
解题注意:“某个力的功”
与“合力的功”
做功对应能量转化的过程,是过程量
二、问题分析
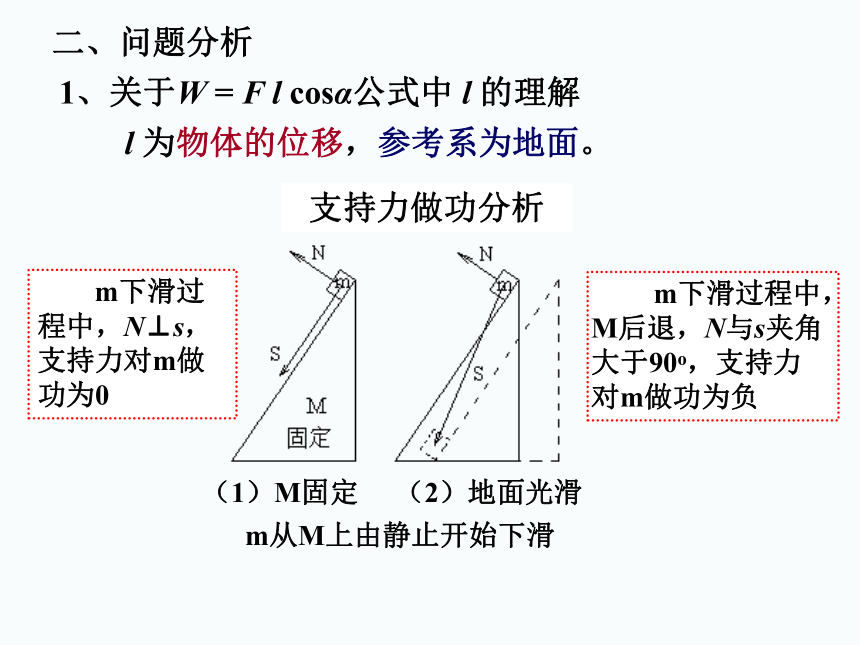
1、关于W
=
F
l
cosα公式中
l
的理解
l
为物体的位移,参考系为地面。
支持力做功分析
m下滑过程中,N⊥s,支持力对m做功为0
(1)M固定
(2)地面光滑
m从M上由静止开始下滑
m下滑过程中,M后退,N与s夹角大于90o,支持力对m做功为负
例1、如图所示,质量为m的物体静止在倾角为θ的斜面上,物体与斜面的动摩擦因数为μ,现使斜面水平向左匀速移动距离l,物体与斜面始终相对静止
(1)摩擦力对物体做的功为
(2)斜面对物体的弹力做的功为
(3)重力对物体做的功为
-m
g
l
sinθcosθ
m
g
l
sinθcosθ
0
例2、带有光滑斜面的物体B放在水平地面上,斜面底端有一重G=2N的金属块A,斜面高h=15
cm,倾角α=60°,用一水平推力F推A,在将A从底端推到顶端的过程中,A和B都做匀速运动,且B运动距离L=30cm,求此过程中力F所做的功和金属块克服斜面支持力所做的功。
N
SN
F的功为
金属块克服斜面支持力的功为
例3、在加速运动的车厢中,一个人用力向前推车厢.如图所示,人相对车厢未移动则下列说法正确的是
A、人对车不做功
B、人对车做负功
C、推力对车做正功
D、车对人做正功
BCD
车对人的水平方向两个作用力,合力向左,车对人做正功
人对车的水平方向两个作用力,合力向右,人对车做负功
若车匀速前进?
例4、如图所示,重球m用轻绳拴住后悬于0点,重球置于一个斜面不光滑的斜劈M上,用水平力F向左推动斜劈M在光滑水平桌面上由位置(a)匀速向左移动到位置(b),在此过程中,正确说法是
A、
m与M之间的摩擦力对m做正功
B、
m与M之间的摩擦力对m做负功
C、
M对m的弹力对m所做的功与m对M的
弹力对M所做的功的绝对值不相等
D、
F对M所做的功与m对M所做的功的绝
对值相等
AD
s
f
s’
N
N’
2、轻绳跨过轻滑轮,绳端拉力的功
例1、如图所示,物体A的质量为2kg
,置于光滑的水平面上,水平拉力F
=2N,不计绳子与滑轮的摩擦和滑轮的质量。在物体A移动
0.4m的过程中,拉力F做的功为多少?
1.6J
例2、如下图所示,物体的质量为m,滑轮的质量和阻力不计,今用一竖直向上的力F=12N向上拉,使物体匀速上升h=4m的高度,则在此过程中拉力所做的功是多少?(取g=10m/s2)
96J
例3、质量为m的物块放在光滑的水平面上.绳经滑轮与水平方向成α角,用大小为F的力拉物块,如图,将物块由A点拉至B点,前进S。
求:拉力所做的功多大?
解法1:F的作用点(绳端)的位移
解法2:力F作用于绳做的功等效于绳对物体做功
3、摩擦力做功
静摩擦力的情况
用力推地上的石头,但是没推动,此时石头与地面有静摩擦力,却没有位移。所以,静摩擦力可以不做功。
静摩擦力的情况
G
N
f
S
物体在传送带上面随传送带一起向上匀速运动,静摩擦力做正功。
静摩擦力的情况
G
N
f
S
物体在传送带上面随传送带一起向下匀速运动,静摩擦力做负功。
滑动摩擦力的情况
质量为M的长木板放在光滑的水平面上,一个质量为m的滑块以某一速度沿木板表面从A滑至B点,在木板上前进了L,而木板前进了S,如图所示。若滑块与木板间的动摩擦因数为μ
,那么摩擦力对滑块和木板各做多少功?
m
m
M
M
A
B
L
S
m
m
M
M
A
B
L
S
f’
f
m受到的摩擦力方向如何?m的位移是多少?位移的方向与摩擦力的方向的夹角又是多少?
对m,摩擦力做功为
M受到的摩擦力的方向如何?大小如何?M的位移大小和方向?
对M,摩擦力做功为
v
f
f
’
滑动摩擦力也可以不做功
小结:
静摩擦力和滑动摩擦力都可以做正功,可以做负功,也可以不做功。
一对滑动摩擦力对物体做功之和必定为负
一对静摩擦力做功之和必定为零
4、作用力与反作用力做功问题
作用力与反作用力同时存在,作用力做功时,反作用力可能做功,也可能不做功,可能做正功,也可能做负功。
(1)可以两个力都不做功;
(2)可以一个力做功,而另一个不做功;
(3)可以一个力做正功,而另一个力做负功;
(4)可以两个力都做正功或都做负功。
5、变力做功问题
微元法
变力做功时,原则上可将位移分成许多极小的小段⊿s,在每一小段上可将变力视为恒力;先求力在⊿s上所做的功,再将各段上的功求代数和即可。
例1、在光滑水平桌面上用一根长1m的细线,系住一个质量m=1kg的小球,使它绕中心点O以v=2m/s匀速圆周运动,小球从某位置起经过半周,绳子拉力做功?经过一周呢?
W=0
推磨的推力呢?
半周
一周
例2、以一定的初速度竖直向上抛出一个小球,小球上升的最大高度为h,空气阻力大小恒为f,则从抛出至回到抛出点的过程,空气阻力对小球做功是多少?
Wf
=-2
f
h
问:则从抛出至回到抛出点的过程,重力的功?
WG
=
0
阻力的功在数值上等于阻力与路程的乘积
例3、如图,一根绳子绕过高4m的滑轮(大小、摩擦均不计),绳的一端拴一质量为10kg的物体,另一侧沿竖直方向的绳被人拉住.若人拉住绳子前进3m,使物体匀速上升,则人拉绳所做的功为
100J
人拉绳
绳拉物
例4、如图所示,定滑轮到滑块高度为H,已知绳拉力F恒定,滑块沿水平地面由A前进s至B点,滑块在初、末位置时细绳与水平方向的夹角为α、β。求
滑块由A点运动到B点过程中,绳子拉力对滑块所做的功。
平均法
当变力与位移成正比时,可采用力在位移中的平均值代入恒力做功的公式,即
F-x图象中的面积代表功的大小
图解法
例5、用铁锤把小铁钉钉入木板,设木板对钉子的阻力与钉进木板的深度成正比,已知铁锤第一次将钉子钉进d,如果铁锤第二次敲钉子时对钉子做的功与第一次相同,那么,第二次钉子进入木板的深度是多少?
例6、如图所示,放在固定斜面上的物体,右端与劲度系数为k的轻质弹簧相连.手以沿斜面向上的力拉弹簧的右端,作用点移动10cm时物体开始滑动,继续缓慢拉弹簧,求当物体位移为0.4m时拉力所做的功?
(k=400N/m)
第七章
机械能守恒定律
伽利略理想斜面实验(接触面均光滑)
A
B
h
h’
α
β
在A斜面上:
在B斜面上:
相互作用的物体凭借其位置而具有的能量,叫做势能。
物体由于运动而具有的能量,叫做动能。
几种常见的能量形式
重力势能(高度)
弹性势能(形变量)
物质都具有各种形式的能量,各种形式的能量都不是孤立的,不同形式的能量会发生相互转化。
如何量度能量转化了多少?
§7.2
功
一、功
1、定义
物体受到力的作用,并在力的方向上发生一段位移,就说该力对物体做了功
2、两个必要条件
(1)力
(2)力的方向上的
位移
推车未动
人对车不做功
小球在水平面上运动,重力及水平面对小球的支持力是否做功?
向心力是否做功?
功是力在空间上的积累
3、功的计算
力对物体所做的功,等于力的大小、位移的大小、力与位移夹角的余弦这三者的乘积。
W
=
F
l
F
2
l
F
F
1
α
F
F
1
F
2
α
W
F2=
0
WF=W
F1
=F1l
=Fl
cosα
W
=
F
l
cosα
公式适用条件:恒力做功
α是
F
与
l
正方向间的夹角
位移
l
为物体的位移,参考系为地面。
功=力乘以力方向的位移
=位移乘以位移方向的力
(2)功的单位:
焦耳(焦、J)
1焦耳=1牛顿·米
意义:1牛的力使物体在力的方向上,通过1米的距离时所做的功为1焦。
(1)公式
例1、两质量相等的物体A、B分别放在粗糙水平面上和光滑的水平面上,在同样的拉力F作用下,产生相同的位移S,则拉力
A、对A做的功多
B、对B做功多
C、一样多
D、以上都有可能
粗糙
光滑
A
B
F
F
θ
θ
C
力对物体做的功只与F、
s、
α三者有关,与物体的运动状态及物体是否还受其他作用力等因素无关。
例2、分别对放在粗糙水平面上的同一物体,施加水平拉力或斜向上的拉力,使物体在这两种情况下的加速度相同,当物体通过相同位移时,这两种情况下拉力的功和合力的功的正确关系是
A.拉力的功和合力的功分别相等
B.拉力的功相等,斜向拉时合力的功大
c.合力的功相等,斜向拉时拉力的功大
D.合力的功相等,斜向拉时拉力的功小
D
4、正功与负功
W
=
F
l
cosα
当α=
0o,W
=
F
l
当α=
90o,W
=
0
当α=
180o,W
=-F
l
当α=
90o,W
=
0,力F不做功
当0≤α<
90o,W
为正值,F对物体做正功
当
90o
<
α≤180o,W
为负值,F对物体做负功,也说,物体克服F做了功
例:滑动摩擦力对物体做功为?10J,
也可以说成物体克服摩擦力做功10J。
功是标量,但有正负,“+”“-”不代表大小。
功的正负只表示动力做功还是阻力做功。
比较功的大小只看绝对值。
例:固定斜面长s,物体质量m,摩擦因数μ,求:物体从斜面顶端滑到底端的过程中各力所做的功。
合力的功=?
5、总功的计算
方法二:分别求出各个外力的功,再把各个外力的功代数相加
方法一:先求出合力,再根据W=F合l
cosα计算功
6、功的物理意义
功是能量转化的量度,是标量
正功代表是动力做功,负功代表阻力做功。
解题注意:“某个力的功”
与“合力的功”
做功对应能量转化的过程,是过程量
二、问题分析
1、关于W
=
F
l
cosα公式中
l
的理解
l
为物体的位移,参考系为地面。
支持力做功分析
m下滑过程中,N⊥s,支持力对m做功为0
(1)M固定
(2)地面光滑
m从M上由静止开始下滑
m下滑过程中,M后退,N与s夹角大于90o,支持力对m做功为负
例1、如图所示,质量为m的物体静止在倾角为θ的斜面上,物体与斜面的动摩擦因数为μ,现使斜面水平向左匀速移动距离l,物体与斜面始终相对静止
(1)摩擦力对物体做的功为
(2)斜面对物体的弹力做的功为
(3)重力对物体做的功为
-m
g
l
sinθcosθ
m
g
l
sinθcosθ
0
例2、带有光滑斜面的物体B放在水平地面上,斜面底端有一重G=2N的金属块A,斜面高h=15
cm,倾角α=60°,用一水平推力F推A,在将A从底端推到顶端的过程中,A和B都做匀速运动,且B运动距离L=30cm,求此过程中力F所做的功和金属块克服斜面支持力所做的功。
N
SN
F的功为
金属块克服斜面支持力的功为
例3、在加速运动的车厢中,一个人用力向前推车厢.如图所示,人相对车厢未移动则下列说法正确的是
A、人对车不做功
B、人对车做负功
C、推力对车做正功
D、车对人做正功
BCD
车对人的水平方向两个作用力,合力向左,车对人做正功
人对车的水平方向两个作用力,合力向右,人对车做负功
若车匀速前进?
例4、如图所示,重球m用轻绳拴住后悬于0点,重球置于一个斜面不光滑的斜劈M上,用水平力F向左推动斜劈M在光滑水平桌面上由位置(a)匀速向左移动到位置(b),在此过程中,正确说法是
A、
m与M之间的摩擦力对m做正功
B、
m与M之间的摩擦力对m做负功
C、
M对m的弹力对m所做的功与m对M的
弹力对M所做的功的绝对值不相等
D、
F对M所做的功与m对M所做的功的绝
对值相等
AD
s
f
s’
N
N’
2、轻绳跨过轻滑轮,绳端拉力的功
例1、如图所示,物体A的质量为2kg
,置于光滑的水平面上,水平拉力F
=2N,不计绳子与滑轮的摩擦和滑轮的质量。在物体A移动
0.4m的过程中,拉力F做的功为多少?
1.6J
例2、如下图所示,物体的质量为m,滑轮的质量和阻力不计,今用一竖直向上的力F=12N向上拉,使物体匀速上升h=4m的高度,则在此过程中拉力所做的功是多少?(取g=10m/s2)
96J
例3、质量为m的物块放在光滑的水平面上.绳经滑轮与水平方向成α角,用大小为F的力拉物块,如图,将物块由A点拉至B点,前进S。
求:拉力所做的功多大?
解法1:F的作用点(绳端)的位移
解法2:力F作用于绳做的功等效于绳对物体做功
3、摩擦力做功
静摩擦力的情况
用力推地上的石头,但是没推动,此时石头与地面有静摩擦力,却没有位移。所以,静摩擦力可以不做功。
静摩擦力的情况
G
N
f
S
物体在传送带上面随传送带一起向上匀速运动,静摩擦力做正功。
静摩擦力的情况
G
N
f
S
物体在传送带上面随传送带一起向下匀速运动,静摩擦力做负功。
滑动摩擦力的情况
质量为M的长木板放在光滑的水平面上,一个质量为m的滑块以某一速度沿木板表面从A滑至B点,在木板上前进了L,而木板前进了S,如图所示。若滑块与木板间的动摩擦因数为μ
,那么摩擦力对滑块和木板各做多少功?
m
m
M
M
A
B
L
S
m
m
M
M
A
B
L
S
f’
f
m受到的摩擦力方向如何?m的位移是多少?位移的方向与摩擦力的方向的夹角又是多少?
对m,摩擦力做功为
M受到的摩擦力的方向如何?大小如何?M的位移大小和方向?
对M,摩擦力做功为
v
f
f
’
滑动摩擦力也可以不做功
小结:
静摩擦力和滑动摩擦力都可以做正功,可以做负功,也可以不做功。
一对滑动摩擦力对物体做功之和必定为负
一对静摩擦力做功之和必定为零
4、作用力与反作用力做功问题
作用力与反作用力同时存在,作用力做功时,反作用力可能做功,也可能不做功,可能做正功,也可能做负功。
(1)可以两个力都不做功;
(2)可以一个力做功,而另一个不做功;
(3)可以一个力做正功,而另一个力做负功;
(4)可以两个力都做正功或都做负功。
5、变力做功问题
微元法
变力做功时,原则上可将位移分成许多极小的小段⊿s,在每一小段上可将变力视为恒力;先求力在⊿s上所做的功,再将各段上的功求代数和即可。
例1、在光滑水平桌面上用一根长1m的细线,系住一个质量m=1kg的小球,使它绕中心点O以v=2m/s匀速圆周运动,小球从某位置起经过半周,绳子拉力做功?经过一周呢?
W=0
推磨的推力呢?
半周
一周
例2、以一定的初速度竖直向上抛出一个小球,小球上升的最大高度为h,空气阻力大小恒为f,则从抛出至回到抛出点的过程,空气阻力对小球做功是多少?
Wf
=-2
f
h
问:则从抛出至回到抛出点的过程,重力的功?
WG
=
0
阻力的功在数值上等于阻力与路程的乘积
例3、如图,一根绳子绕过高4m的滑轮(大小、摩擦均不计),绳的一端拴一质量为10kg的物体,另一侧沿竖直方向的绳被人拉住.若人拉住绳子前进3m,使物体匀速上升,则人拉绳所做的功为
100J
人拉绳
绳拉物
例4、如图所示,定滑轮到滑块高度为H,已知绳拉力F恒定,滑块沿水平地面由A前进s至B点,滑块在初、末位置时细绳与水平方向的夹角为α、β。求
滑块由A点运动到B点过程中,绳子拉力对滑块所做的功。
平均法
当变力与位移成正比时,可采用力在位移中的平均值代入恒力做功的公式,即
F-x图象中的面积代表功的大小
图解法
例5、用铁锤把小铁钉钉入木板,设木板对钉子的阻力与钉进木板的深度成正比,已知铁锤第一次将钉子钉进d,如果铁锤第二次敲钉子时对钉子做的功与第一次相同,那么,第二次钉子进入木板的深度是多少?
例6、如图所示,放在固定斜面上的物体,右端与劲度系数为k的轻质弹簧相连.手以沿斜面向上的力拉弹簧的右端,作用点移动10cm时物体开始滑动,继续缓慢拉弹簧,求当物体位移为0.4m时拉力所做的功?
(k=400N/m)
