人教版高中物理选修3-1 第三章 3.6带电粒子在匀强磁场中的运动课件(共44张PPT)
文档属性
| 名称 | 人教版高中物理选修3-1 第三章 3.6带电粒子在匀强磁场中的运动课件(共44张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-08-25 00:00:00 | ||
图片预览









文档简介
(共44张PPT)
§3、6
带电粒子在匀强磁场中的运动
磁场中的带电体一般可分为两类:
1、电子,质子,α粒子,离子等。一般不计重力(不能忽略质量)。
2、质量较大的质点:带电微粒、液滴等。一般不忽略重力。
带电体是否考虑重力,要根据题目暗示或运动状态来判定。
一、只在洛伦兹力作用下,带电粒子在匀强磁场中的运动
1、若v∥B,则F洛=
0,带电粒子以速度v做匀速直线运动
2、若v⊥B,则F洛=
Bqv,带电粒子在垂直于磁感线的平面内做匀速圆周运动
(1)向心力由洛伦兹力提供,
即
(2)轨道半径:
(3)周期:
周期与速度无关
频率:
角速度:
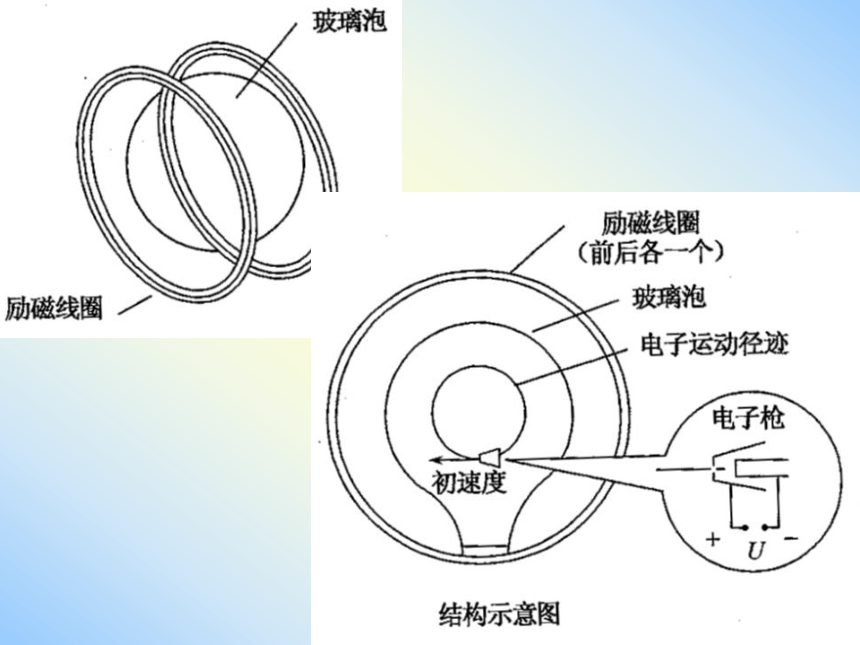
实验验证:洛伦兹力演示仪
构造:①电子枪:射出电子;②加速电场:给电子加速;③励磁线圈:在两线圈之间产生垂直于线圈平面的匀强磁场。
工作原理:
加速后的电子可以使管内的低压水银蒸汽发出辉光,显示出电子的径迹。
电子束的磁偏转
在演示仪中可以观察到:没有磁场时,电子束是直进的;外加磁场后,电子束的径迹变成圆形。磁场的强弱和电子的速度都能影响圆的半径。
带电粒子在汽泡室运动径迹的照片。有的粒子运动过程中能量降低,速度减小,径迹就呈螺旋形。
3、若v与B之间的夹角θ,则带电粒子的运动轨迹为?
以速度v1做匀速直线运动
以速度v2做匀速圆周运动
等距螺旋线
d
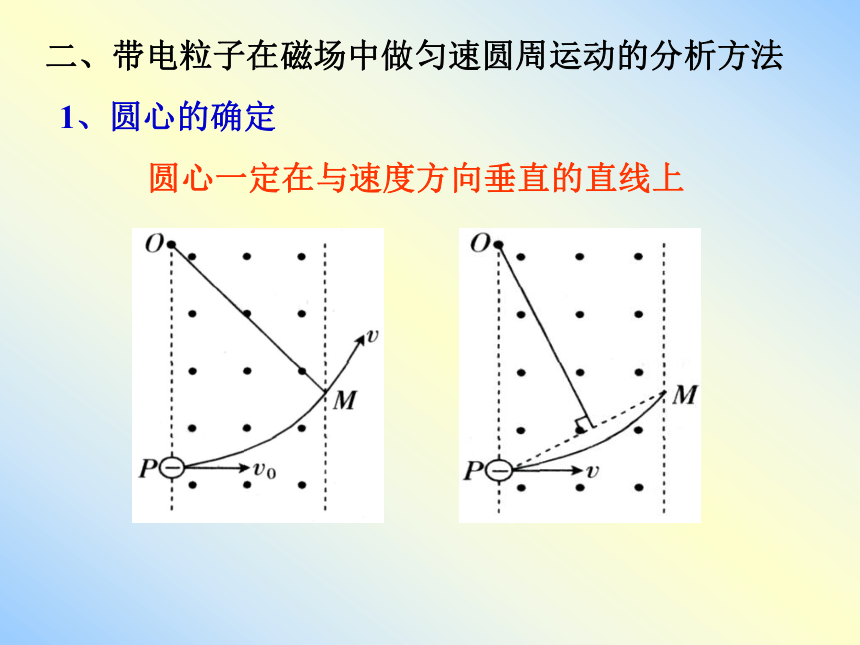
二、带电粒子在磁场中做匀速圆周运动的分析方法
1、圆心的确定
圆心一定在与速度方向垂直的直线上
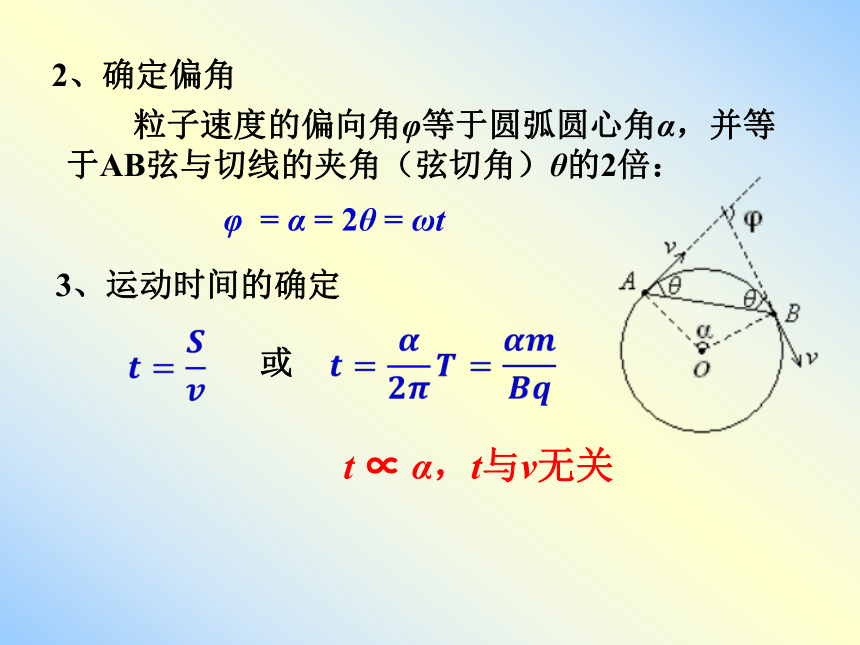
2、确定偏角
粒子速度的偏向角φ等于圆弧圆心角α,并等于AB弦与切线的夹角(弦切角)θ的2倍:
φ
=
α
=
2θ
=
ωt
3、运动时间的确定
或
t
∝
α,t与v无关
方法总结:①画轨迹②定圆心③求半径、时间
找圆心:
定半径:
定时间:
α用弧度表示
利用F⊥v
利用弦的中垂线
几何法求半径
公式求半径
(一)单边界场
例1、如图示,m,+q的粒子,不计重力,垂直边界以v射入匀强磁场B,试求射出点和射入点之间的距离和在磁场中运动时间。
A
例2、如图示,m,+q的粒子,不计重力,从A与边界成30°以速度v射入匀强磁场B,试求:
(1)射出点和射入点之间的距离
(2)在磁场中的运动时间
A
若换成?q?
+q、?q进出磁场位移大小一样。
(二)双边有界场
d
B
e
v
θ
θ
O
O
θ
a
o
(三)圆形有界场
圆形磁场区域的对称特点:
若粒子沿磁场半径方向入射,
则一定沿磁场另一条半径方向出射。
在两交点上同一圆的两条切线AC和BC如果相交,则一定交于两圆心连线OO′的同一点C。
粒子轨迹圆与磁场边界圆的相交:
O'
O
A
B
C
(四)带电粒子在磁场中运动的多解问题
(1)带电粒子电性不确定
(3)临界状态不唯一
(4)运动的重复性
(2)磁场方向不确定
(5)运动方向不确定
(五)动态圆分析法
一束带负电的粒子从同一点A垂直进入匀强磁场,初速方向相同,但v大小不同:
①所有粒子运动轨迹的圆心都在垂直于初速的直线上;
②速度大的,轨迹半径大;
③所有粒子的轨迹过A点,组成一组内切圆。
一束带负电的粒子从同一点以相同的速率v0垂直进入于匀强磁场,初速方向不同:
规律:带电粒子电性决定圆周运动的环绕方向,与入射速度方向无关!
①所有轨迹相交于A点
;
②所有轨迹的半径
相等,
所有粒子运动轨迹的圆心都在以
A为圆心,R为半径的圆上
③所有粒子绕向相同
例1、如图,水平板MN上方有匀强磁场B,许多质量m带电量+q的粒子,以相同的速率v0沿位于纸面内的各个方向运动,由小孔O射入磁场区域,不计重力,不计粒子间的互相影响。下面图中的阴影部分表示带电粒子可能经过的区域,其中
。哪个图是正确的
A
例2、
如图所示,磁感应强度为B的匀强磁场垂直于纸面向里,PQ为该磁场的右侧边界线,磁场中有一点O,O点到PQ的距离为r。现从点O以同一速率将相同的带负电粒子向纸面内各个不同的方向射出,它们均做半径为r的匀速圆周运动,求带电粒子打在边界PQ上的范围(粒子的重力不计)。
三、重要应用
(一)质谱仪
容器A中含有电荷量相同而质量有微小差别的粒子,粒子经S1、S2两极间的电压U加速后由S3进入匀强磁场
因为
所以
质谱仪最初是由汤姆生的学生阿斯顿设计的,他用质谱仪发现了氖20和氖22,证实了同位素的存在。现在质谱仪已经是一种十分精密的仪器,是测量带电粒子的质量和分析同位素的重要工具。
(二)粒子加速器
利用电场加速带电粒子
+
U
+
+
+
如何使粒子获得更大的速度(能量)?
采用多个电场,使带电粒子多级加速
加速
加速
加速
加速
改进办法:利用静电屏蔽,使用交流电源
筒间加速
筒内匀速
为了实现带电粒子的多级加速,应该采用交变电源,使粒子每次到达筒间都能加速。电源极性的变化要与粒子的运动配合,步调一致,即满足同步条件。由此根据交流电的周期和粒子运动速度,设置筒长、筒间距。
用金属圆筒代替极板,在金属圆筒的间隙处形成加速电场;在圆筒内部的场强为零,粒子匀速。
直线加速器
多级直线加速器应具备的条件:
①利用电场加速带电粒子;
②通过多级加速获得高能粒子;
③加速电场以外的区域静电屏蔽,粒子匀速;
④采用交变电源提供加速电压;
⑤电场交替变化与带电粒子运动应满足同步条件。
回旋加速器
1、结构:
它的核心结构是两个D形的金属盒,两个D形盒接在高频交流电电极上。D形盒中间有一个窄缝,中心附近有一个粒子源。整个装置放在巨大的电磁铁的两极之间。加速后的粒子最后由特殊装置引出。
2、原理
用磁场控制轨道、用电场进行加速
问题1:粒子被加速后,运动速率和运动半径都会增加,它的运动周期会变化吗?
问题2:在回旋加速器中,如果两个D型盒接在直流电源上,那么带电粒子能否被加速?
交变电压:
保证带电粒子每次经过窄缝时都被加速。
不变
为使带电粒子不断得到加速,提供的电压应符合怎样的要求?
交变电压的周期TE
=
粒子在磁场中运动的周期TB
一个周期内,粒子加速两次
问题3:要提高加速粒子的最后能量,可以采取哪些措施?
∵运动半径最大
得
∴半径最大时,速度也应最大。
∴带电粒子的运动最大半径等于D形盒的半径时,粒子的速度达到最大。
尽可能增大磁感应强度B和加速器最大半径Rm
增大加速电压?
没用
问题4:D形盒的直径为D,粒子的最大动能
D越大,Ek越大,是不是只要D不断增大,
Ek
就可以无限制增大呢?
不行。用这种经典的回旋加速器来加速粒子,能量达到25~30MeV后,就很难再加速了。因为当粒子的速率大到接近光速时,由相对论原理,粒子的质量明显增大,从而使粒子的回旋周期变化,这就破坏了加速器的同步条件。
3、总结
(1)
粒子在匀强磁场中的运动周期不变
(2)交变电场的周期和粒子的运动周期T相同——保证粒子每次经过交变电场时都被加速
一个周期内,粒子加速两次
(3)带电粒子每经电场加速一次,回旋半径就增大一次,每次增加的动能为
各次半径之比为
(4)粒子的最大速度由盒的半径决定
(5)粒子转过的圈数?运动的总时间?
被加速的次数?
四、带电体在复合场中的运动分析
辨析:“电偏转”和“磁偏转”的差别
(1)受力特征
(2)运动规律
(3)偏转情况
(4)做功特点
问题分析:A、B、C是三只完全相同的带正电小球,从同一高度开始自由下落,A球穿过一个垂直纸面向内的匀强磁场;B球下落过程中穿过水平方向的匀强电场;C球直接落地。若不计空气阻力,试比较它们落地时间、落地速率的大小关系。
(一)组合场问题
运动分析的联系点是速度
速度不能突变,在前一个场中的运动的末速度,就是后一个场中运动的初速度。
例、如图,y>0空间匀强电场;y<0空间匀强磁场。离子m、
+q,经P1(0,h)时v0沿x轴正方向;然后,经P2(2h,0)进入磁场,并经过P3点(0,-2h
)
。求:(1)E(2)粒子到P2时的速度(3)B
电场内:类平抛运动
磁场内:圆周运动
与x轴正向成45°向下
(二)复合场中的直线运动
例1、如图所示,匀强电场方向水平向右,匀强磁场方向垂直于纸面向里。一质量为m、带电荷量为q的微粒以速度v与磁场垂直、与电场成θ角射入复合场中,恰能做匀速直线运动,已知重力加速度为g。
(1)请判断微粒的带电性质
(2)求电场强度E和磁感应强度B的大小
正电荷
例2、小球(
m,
+q
)套在很长的绝缘直棒上,可在棒上滑动,将此棒竖直放在如图所示的匀强电场E和匀强磁场B中,动摩擦因数为μ,请定性描述小球的运动过程,并求小球由静止沿棒下落的最大加速度和最大速度。
小球从静止开始做加速度逐渐减小的加速运动,最后保持匀速运动状态
最大加速度出现在v
=
0时
最大速度出现在a
=0时
若电场反向,情况如何?
小球从静止开始先做加速度逐渐增大的加速运动,加速度最大为g,然后做加速度逐渐减小的加速运动,最后a
=0,小球保持匀速直线运动状态。
最大加速度出现在洛伦兹力与电场力等大反向
Bqv=Eq
时,a=g,此时小球所受的摩擦为0
加速度a
=0时出现最大速度
(三)复合场中的曲线运动
例1、液滴(m,q)在竖直面内以速度v匀速圆周运动,则此液滴带
电,电场强度
,从最高点到最低点,电场力做功为
。
负
例2、如图所示,小球(m,+q)套在半径为R的光滑绝缘竖直环上,匀强电场和匀强磁场水平正交,已知小球所受电场力与重力的大小相等,磁感应强度B
。在环顶端处无初速释放小球,小球的运动过程中所受的最大洛伦兹力?
引入“等效场”
最大速度
要使套在环上的小球能沿环做完整的圆周运动,只要能使小球通过环上的复合场的最高点D即可
例3、如图所示,直角坐标系xOy位于竖直平面内,在该空间内有一沿水平方向足够长的匀强磁场区域,磁场方向垂直于xOy平面向里,磁感应强度为B、磁场区域的上、下边界面距离x轴的距离均为d,一质量为m、电荷量为q的带正电的微粒从坐标原点O沿+x方向发射。
(1)若欲使该微粒发射后一直沿x轴运动,求发射速度v0
(2)若欲使发射后不从磁场区域的上界面飞出磁场,求发射速度允许的最大值v0m
运动分解!
讨论:
(2)运动的周期性:
经过一个周期
微粒将回到x轴上,此时的坐标位置
该微粒经过
,将到达最高点,最高点的坐标为
(1)运动分解:以v0匀速直线,以⊿v匀速圆周
(3)若要使微粒不从下边界飞出磁场区域,则从坐标原点在平行于x轴的方向上发射微粒的速度临界值应为多大?
(4)当磁场区域足够大,让微粒从坐标原点由静止释放,它的运动情况是怎样的?能否继续用运动的合成与分解原理来研究?试定性画出运动轨迹。
§3、6
带电粒子在匀强磁场中的运动
磁场中的带电体一般可分为两类:
1、电子,质子,α粒子,离子等。一般不计重力(不能忽略质量)。
2、质量较大的质点:带电微粒、液滴等。一般不忽略重力。
带电体是否考虑重力,要根据题目暗示或运动状态来判定。
一、只在洛伦兹力作用下,带电粒子在匀强磁场中的运动
1、若v∥B,则F洛=
0,带电粒子以速度v做匀速直线运动
2、若v⊥B,则F洛=
Bqv,带电粒子在垂直于磁感线的平面内做匀速圆周运动
(1)向心力由洛伦兹力提供,
即
(2)轨道半径:
(3)周期:
周期与速度无关
频率:
角速度:
实验验证:洛伦兹力演示仪
构造:①电子枪:射出电子;②加速电场:给电子加速;③励磁线圈:在两线圈之间产生垂直于线圈平面的匀强磁场。
工作原理:
加速后的电子可以使管内的低压水银蒸汽发出辉光,显示出电子的径迹。
电子束的磁偏转
在演示仪中可以观察到:没有磁场时,电子束是直进的;外加磁场后,电子束的径迹变成圆形。磁场的强弱和电子的速度都能影响圆的半径。
带电粒子在汽泡室运动径迹的照片。有的粒子运动过程中能量降低,速度减小,径迹就呈螺旋形。
3、若v与B之间的夹角θ,则带电粒子的运动轨迹为?
以速度v1做匀速直线运动
以速度v2做匀速圆周运动
等距螺旋线
d
二、带电粒子在磁场中做匀速圆周运动的分析方法
1、圆心的确定
圆心一定在与速度方向垂直的直线上
2、确定偏角
粒子速度的偏向角φ等于圆弧圆心角α,并等于AB弦与切线的夹角(弦切角)θ的2倍:
φ
=
α
=
2θ
=
ωt
3、运动时间的确定
或
t
∝
α,t与v无关
方法总结:①画轨迹②定圆心③求半径、时间
找圆心:
定半径:
定时间:
α用弧度表示
利用F⊥v
利用弦的中垂线
几何法求半径
公式求半径
(一)单边界场
例1、如图示,m,+q的粒子,不计重力,垂直边界以v射入匀强磁场B,试求射出点和射入点之间的距离和在磁场中运动时间。
A
例2、如图示,m,+q的粒子,不计重力,从A与边界成30°以速度v射入匀强磁场B,试求:
(1)射出点和射入点之间的距离
(2)在磁场中的运动时间
A
若换成?q?
+q、?q进出磁场位移大小一样。
(二)双边有界场
d
B
e
v
θ
θ
O
O
θ
a
o
(三)圆形有界场
圆形磁场区域的对称特点:
若粒子沿磁场半径方向入射,
则一定沿磁场另一条半径方向出射。
在两交点上同一圆的两条切线AC和BC如果相交,则一定交于两圆心连线OO′的同一点C。
粒子轨迹圆与磁场边界圆的相交:
O'
O
A
B
C
(四)带电粒子在磁场中运动的多解问题
(1)带电粒子电性不确定
(3)临界状态不唯一
(4)运动的重复性
(2)磁场方向不确定
(5)运动方向不确定
(五)动态圆分析法
一束带负电的粒子从同一点A垂直进入匀强磁场,初速方向相同,但v大小不同:
①所有粒子运动轨迹的圆心都在垂直于初速的直线上;
②速度大的,轨迹半径大;
③所有粒子的轨迹过A点,组成一组内切圆。
一束带负电的粒子从同一点以相同的速率v0垂直进入于匀强磁场,初速方向不同:
规律:带电粒子电性决定圆周运动的环绕方向,与入射速度方向无关!
①所有轨迹相交于A点
;
②所有轨迹的半径
相等,
所有粒子运动轨迹的圆心都在以
A为圆心,R为半径的圆上
③所有粒子绕向相同
例1、如图,水平板MN上方有匀强磁场B,许多质量m带电量+q的粒子,以相同的速率v0沿位于纸面内的各个方向运动,由小孔O射入磁场区域,不计重力,不计粒子间的互相影响。下面图中的阴影部分表示带电粒子可能经过的区域,其中
。哪个图是正确的
A
例2、
如图所示,磁感应强度为B的匀强磁场垂直于纸面向里,PQ为该磁场的右侧边界线,磁场中有一点O,O点到PQ的距离为r。现从点O以同一速率将相同的带负电粒子向纸面内各个不同的方向射出,它们均做半径为r的匀速圆周运动,求带电粒子打在边界PQ上的范围(粒子的重力不计)。
三、重要应用
(一)质谱仪
容器A中含有电荷量相同而质量有微小差别的粒子,粒子经S1、S2两极间的电压U加速后由S3进入匀强磁场
因为
所以
质谱仪最初是由汤姆生的学生阿斯顿设计的,他用质谱仪发现了氖20和氖22,证实了同位素的存在。现在质谱仪已经是一种十分精密的仪器,是测量带电粒子的质量和分析同位素的重要工具。
(二)粒子加速器
利用电场加速带电粒子
+
U
+
+
+
如何使粒子获得更大的速度(能量)?
采用多个电场,使带电粒子多级加速
加速
加速
加速
加速
改进办法:利用静电屏蔽,使用交流电源
筒间加速
筒内匀速
为了实现带电粒子的多级加速,应该采用交变电源,使粒子每次到达筒间都能加速。电源极性的变化要与粒子的运动配合,步调一致,即满足同步条件。由此根据交流电的周期和粒子运动速度,设置筒长、筒间距。
用金属圆筒代替极板,在金属圆筒的间隙处形成加速电场;在圆筒内部的场强为零,粒子匀速。
直线加速器
多级直线加速器应具备的条件:
①利用电场加速带电粒子;
②通过多级加速获得高能粒子;
③加速电场以外的区域静电屏蔽,粒子匀速;
④采用交变电源提供加速电压;
⑤电场交替变化与带电粒子运动应满足同步条件。
回旋加速器
1、结构:
它的核心结构是两个D形的金属盒,两个D形盒接在高频交流电电极上。D形盒中间有一个窄缝,中心附近有一个粒子源。整个装置放在巨大的电磁铁的两极之间。加速后的粒子最后由特殊装置引出。
2、原理
用磁场控制轨道、用电场进行加速
问题1:粒子被加速后,运动速率和运动半径都会增加,它的运动周期会变化吗?
问题2:在回旋加速器中,如果两个D型盒接在直流电源上,那么带电粒子能否被加速?
交变电压:
保证带电粒子每次经过窄缝时都被加速。
不变
为使带电粒子不断得到加速,提供的电压应符合怎样的要求?
交变电压的周期TE
=
粒子在磁场中运动的周期TB
一个周期内,粒子加速两次
问题3:要提高加速粒子的最后能量,可以采取哪些措施?
∵运动半径最大
得
∴半径最大时,速度也应最大。
∴带电粒子的运动最大半径等于D形盒的半径时,粒子的速度达到最大。
尽可能增大磁感应强度B和加速器最大半径Rm
增大加速电压?
没用
问题4:D形盒的直径为D,粒子的最大动能
D越大,Ek越大,是不是只要D不断增大,
Ek
就可以无限制增大呢?
不行。用这种经典的回旋加速器来加速粒子,能量达到25~30MeV后,就很难再加速了。因为当粒子的速率大到接近光速时,由相对论原理,粒子的质量明显增大,从而使粒子的回旋周期变化,这就破坏了加速器的同步条件。
3、总结
(1)
粒子在匀强磁场中的运动周期不变
(2)交变电场的周期和粒子的运动周期T相同——保证粒子每次经过交变电场时都被加速
一个周期内,粒子加速两次
(3)带电粒子每经电场加速一次,回旋半径就增大一次,每次增加的动能为
各次半径之比为
(4)粒子的最大速度由盒的半径决定
(5)粒子转过的圈数?运动的总时间?
被加速的次数?
四、带电体在复合场中的运动分析
辨析:“电偏转”和“磁偏转”的差别
(1)受力特征
(2)运动规律
(3)偏转情况
(4)做功特点
问题分析:A、B、C是三只完全相同的带正电小球,从同一高度开始自由下落,A球穿过一个垂直纸面向内的匀强磁场;B球下落过程中穿过水平方向的匀强电场;C球直接落地。若不计空气阻力,试比较它们落地时间、落地速率的大小关系。
(一)组合场问题
运动分析的联系点是速度
速度不能突变,在前一个场中的运动的末速度,就是后一个场中运动的初速度。
例、如图,y>0空间匀强电场;y<0空间匀强磁场。离子m、
+q,经P1(0,h)时v0沿x轴正方向;然后,经P2(2h,0)进入磁场,并经过P3点(0,-2h
)
。求:(1)E(2)粒子到P2时的速度(3)B
电场内:类平抛运动
磁场内:圆周运动
与x轴正向成45°向下
(二)复合场中的直线运动
例1、如图所示,匀强电场方向水平向右,匀强磁场方向垂直于纸面向里。一质量为m、带电荷量为q的微粒以速度v与磁场垂直、与电场成θ角射入复合场中,恰能做匀速直线运动,已知重力加速度为g。
(1)请判断微粒的带电性质
(2)求电场强度E和磁感应强度B的大小
正电荷
例2、小球(
m,
+q
)套在很长的绝缘直棒上,可在棒上滑动,将此棒竖直放在如图所示的匀强电场E和匀强磁场B中,动摩擦因数为μ,请定性描述小球的运动过程,并求小球由静止沿棒下落的最大加速度和最大速度。
小球从静止开始做加速度逐渐减小的加速运动,最后保持匀速运动状态
最大加速度出现在v
=
0时
最大速度出现在a
=0时
若电场反向,情况如何?
小球从静止开始先做加速度逐渐增大的加速运动,加速度最大为g,然后做加速度逐渐减小的加速运动,最后a
=0,小球保持匀速直线运动状态。
最大加速度出现在洛伦兹力与电场力等大反向
Bqv=Eq
时,a=g,此时小球所受的摩擦为0
加速度a
=0时出现最大速度
(三)复合场中的曲线运动
例1、液滴(m,q)在竖直面内以速度v匀速圆周运动,则此液滴带
电,电场强度
,从最高点到最低点,电场力做功为
。
负
例2、如图所示,小球(m,+q)套在半径为R的光滑绝缘竖直环上,匀强电场和匀强磁场水平正交,已知小球所受电场力与重力的大小相等,磁感应强度B
。在环顶端处无初速释放小球,小球的运动过程中所受的最大洛伦兹力?
引入“等效场”
最大速度
要使套在环上的小球能沿环做完整的圆周运动,只要能使小球通过环上的复合场的最高点D即可
例3、如图所示,直角坐标系xOy位于竖直平面内,在该空间内有一沿水平方向足够长的匀强磁场区域,磁场方向垂直于xOy平面向里,磁感应强度为B、磁场区域的上、下边界面距离x轴的距离均为d,一质量为m、电荷量为q的带正电的微粒从坐标原点O沿+x方向发射。
(1)若欲使该微粒发射后一直沿x轴运动,求发射速度v0
(2)若欲使发射后不从磁场区域的上界面飞出磁场,求发射速度允许的最大值v0m
运动分解!
讨论:
(2)运动的周期性:
经过一个周期
微粒将回到x轴上,此时的坐标位置
该微粒经过
,将到达最高点,最高点的坐标为
(1)运动分解:以v0匀速直线,以⊿v匀速圆周
(3)若要使微粒不从下边界飞出磁场区域,则从坐标原点在平行于x轴的方向上发射微粒的速度临界值应为多大?
(4)当磁场区域足够大,让微粒从坐标原点由静止释放,它的运动情况是怎样的?能否继续用运动的合成与分解原理来研究?试定性画出运动轨迹。
