14.2.2 完全平方公式课件(26张PPT)
文档属性
| 名称 | 14.2.2 完全平方公式课件(26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-25 00:00:00 | ||
图片预览








文档简介
第 十四 章 整式的乘法与因式分解14.2 乘法公式
14.2.2 完全平方公式
2020年秋人教版数学八年级上册精品课件
学 习 目 标
1
2
理解并掌握完全平方公式的推导过程和结构特征.(重点)
会灵活运用完全平方公式进行计算.(难点)
知识讲解
多项式与多项式的乘法法则
(a+b)(m+n)=am+an+bm+bn.
计算下列各题,你能发现什么规律?
想一想:这些计算结果有什么规律和特点?
(1)(p+1)2=(p+1)(p+1)= ;
p2+2p+1
(2)(m+2)2=(m+2)(m+2)= ;
m2+4m+4
(3)(p-1)2=(p-1)(p-1)= ;
p2-2p+1
(4)(m-2)2=(m-2)(m-2)= .
m2-4m+4
(a+b)2= ;
a2+2ab+b2
(a-b)2= .
a2-2ab+b2
根据你发现的规律,计算下列式子:
(????+????)2=(????+????)(????+????)=????2+????????+????????+????2=????2+2????????+????2.
(?????????)2=(?????????)(?????????)=????2-????????-????????+????2=????2-2????????+????2.
?
证明:
(a+b)2= ,
a2+2ab+b2
(a-b)2= .
a2-2ab+b2
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.这两个公式叫做(乘法的)完全平方公式.
完全平方公式:
????
?
????
?
????
?
????
?
(????+????)?
?
?????
?
?????
?
????????
?
+
+
完全平方和公式:
????????
?
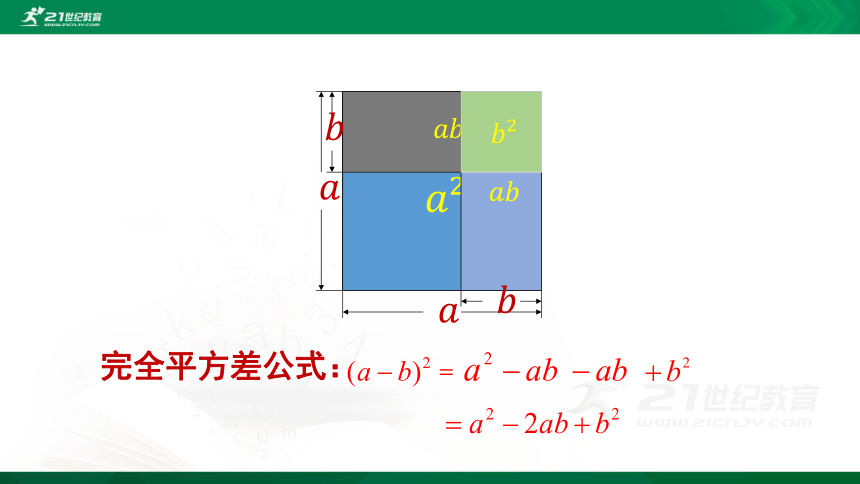
其实我们还可以从几何角度去解释完全平方公式.
????
?
????
?
?????
?
????????
?
????????
?
?????
?
????
?
????
?
完全平方差公式:
=
?
完全平方公式有什么特征?
(a+b)2= ,
a2+2ab+b2
(a-b)2= .
a2-2ab+b2
3.公式中的字母a,b可以表示数、单项式或多项式.
1.两个公式的左边都是一个二项式的平方,两者仅有一个“符号”不同;
2. 右边都是二次三项式,其中两项为左边两数的平方和,另一项是左边两数积的2倍,且与两数中间的符号相同;
速记口诀:首平方,尾平方,积的2倍在中央,符号确定看前方.
在下列多项式的乘法中,能用完全平方公式计算的请填Y,不能用的请填N.
(?????+2????)2??????????????????????????( )
(????+2????)(?????2????)??????????????( )
(1+????)(????+1)????????????????????( )
(??3?????????????)(3????????+????)??????( )
(????2?????)(????+????2)????????????????( )
(?100?1)(100+1)?????????( )
(7) (??????????????)2???????????????????????? ( )
?
Y
N
Y
N
N
N
Y
判一判:
例1
运用完全平方公式计算:
解:(1)(????+2????)2=
?
????2
?
(1)(????+2????)2
?
+4????????
?
+4????2
?
(2)(-????2+????3)2
?
(2)(-????2+????3)2= (????3?????2)2
?
=????6?2?????2?????3+????4
?
运用完全平方公式计算:
(1)1022 (2)1992
(3)4982 (4)79.82
解:(1)1022 = (100+2)2
= 1002+2×100×2+22
= 10000+400+4
= 10404
(2)1992 = (200-1)2 =2002-2×200×1+12
= 40000-400+1
= 39601
例2
运用完全平方公式计算:
(1)1022 (2)1992
(3)4982 (4)79.82
例2
解:(3)4982 = (500-2)2
= 5002-2×500×2+22
= 250000-2000+4 = 248004
(4)79.82 = (80-0.2)2
=802-2×80×0.2+0.22
= 6400-32+0.04
= 6368.04
例3
已知x-y=6,xy=-8,求:
(1) x2+y2的值;
(2)(x+y)2的值.
=36-16=20.
解:(1)∵x-y=6,xy=-8,
(x-y)2=x2+y2-2xy,
∴x2+y2=(x-y)2+2xy
(2)∵x2+y2=20,xy=-8,
∴(x+y)2=x2+y2+2xy
=20-16=4.
(1) (??????-????)2 与(????+????)2
?
比较下列各式之间的关系:
相等
(2) (?????-????)2 与(???? ??????)2
?
(3) (-????+ ????)2 与(?????+????)2
?
相等
相等
(1)(-2m-3n) ;
计算:
2
(2)
解:(1)原式=[-(2m+3n)]2
=(2m+3n)2
=(2m)2 +2·2m·3n+(3n)2
=4m2+12mn+9n2.
例4
如何用乘法公式求????+????+?????????
?
a+(b+c) = a+b+c;
a- (b+c) = a - b – c.
a + b + c = a + ( b + c) ;
a – b – c = a – ( b + c ) .
去括号法则:
反过来,就得到添括号法则:
添括号时,如果括号前面是正号,括到括号里的各项都不变符号;如果括号前面是负号,括到括号里的各项都改变符号(简记为“负变正不变”).
先变形
运用乘法公式计算:
(1) (x+2y-3)(x-2y+3) ; (2) (a+b+c)2.
解:
= [(a+b)+c]2
= x2-(2y-3)2
= x2-(4y2-12y+9)
= x2-4y2+12y-9.
= (a+b)2+2(a+b)c+c2
=a2+2ab+b2+2ac+2bc+c2
=a2+b2+c2+2ab+2ac+2bc.
例5
(x+2y-3)(x-2y+3)
=[x+(2y–3)][x-(2y-3)]
(1)
(2)(a+b+c)2
1.下列计算正确的是( )
A.(a+m)2=a2+m2
B.(s-t)2=s2-t2
随堂训练
C
D.(m+n)2=m2+mn+n2
2、若????+????=4,则????2+2????????+????2的值
是( )
A、8 B、16 C、2 D、4
?
B
(?2????????)
?
6、如果
8
?
5.
3.小兵计算一个二项整式的平方式时,得到
正确结果是4????2+ +25????2,但中间一项
不慎被污染了,这一项应是( )
A 10????????? B 20???????? C±10???????? D±20?????????
?
D
4.如果x2-6x+N是一个完全平方式,那么N是( )
A、11 B、9 C、-11 D、-9
B
解:(1)原式=[(x+1)+(y-z)][(x+1)-(y-z)]
=(x+1)2-(y
7.运用乘法公式计算:
(1)(x+y-z+1)(x-y+z+1);
(2)(a-b-c)2.
-z)2
=x2+2x+1-y2+2yz-z2.
(2)原式=[(a-b)-c]2
=(a-b)2-2(a-b)·c+c2
=a2+b2+c2
-2ab+2bc-2ac.
8.若a+b=5,ab=-6,求a2+b2,a2-ab+b2.
9.已知x+y=8,x-y=4,求xy.
解:∵a+b=5,ab=-6,
∴a2+b2=(a+b)2-2ab=52-2×(-6)=37;
解:∵x+y=8,∴(x+y)2=64,即x2+y2+2xy=64①.
∵x-y=4, ∴(x-y)2=16,即x2+y2-2xy=16②.
①-②,得
4xy=48,
∴xy=12.
a2-ab+b2=a2+b2-ab=37-(-6)=43.
课堂小结
(a+b)2= ,
a2+2ab+b2
(a-b)2= .
a2-2ab+b2
1.完全平方公式:
a + b + c = a + ( b + c) ;
a – b – c = a – ( b + c ) .
2.添括号法则:
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
14.2.2 完全平方公式
2020年秋人教版数学八年级上册精品课件
学 习 目 标
1
2
理解并掌握完全平方公式的推导过程和结构特征.(重点)
会灵活运用完全平方公式进行计算.(难点)
知识讲解
多项式与多项式的乘法法则
(a+b)(m+n)=am+an+bm+bn.
计算下列各题,你能发现什么规律?
想一想:这些计算结果有什么规律和特点?
(1)(p+1)2=(p+1)(p+1)= ;
p2+2p+1
(2)(m+2)2=(m+2)(m+2)= ;
m2+4m+4
(3)(p-1)2=(p-1)(p-1)= ;
p2-2p+1
(4)(m-2)2=(m-2)(m-2)= .
m2-4m+4
(a+b)2= ;
a2+2ab+b2
(a-b)2= .
a2-2ab+b2
根据你发现的规律,计算下列式子:
(????+????)2=(????+????)(????+????)=????2+????????+????????+????2=????2+2????????+????2.
(?????????)2=(?????????)(?????????)=????2-????????-????????+????2=????2-2????????+????2.
?
证明:
(a+b)2= ,
a2+2ab+b2
(a-b)2= .
a2-2ab+b2
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.这两个公式叫做(乘法的)完全平方公式.
完全平方公式:
????
?
????
?
????
?
????
?
(????+????)?
?
?????
?
?????
?
????????
?
+
+
完全平方和公式:
????????
?
其实我们还可以从几何角度去解释完全平方公式.
????
?
????
?
?????
?
????????
?
????????
?
?????
?
????
?
????
?
完全平方差公式:
=
?
完全平方公式有什么特征?
(a+b)2= ,
a2+2ab+b2
(a-b)2= .
a2-2ab+b2
3.公式中的字母a,b可以表示数、单项式或多项式.
1.两个公式的左边都是一个二项式的平方,两者仅有一个“符号”不同;
2. 右边都是二次三项式,其中两项为左边两数的平方和,另一项是左边两数积的2倍,且与两数中间的符号相同;
速记口诀:首平方,尾平方,积的2倍在中央,符号确定看前方.
在下列多项式的乘法中,能用完全平方公式计算的请填Y,不能用的请填N.
(?????+2????)2??????????????????????????( )
(????+2????)(?????2????)??????????????( )
(1+????)(????+1)????????????????????( )
(??3?????????????)(3????????+????)??????( )
(????2?????)(????+????2)????????????????( )
(?100?1)(100+1)?????????( )
(7) (??????????????)2???????????????????????? ( )
?
Y
N
Y
N
N
N
Y
判一判:
例1
运用完全平方公式计算:
解:(1)(????+2????)2=
?
????2
?
(1)(????+2????)2
?
+4????????
?
+4????2
?
(2)(-????2+????3)2
?
(2)(-????2+????3)2= (????3?????2)2
?
=????6?2?????2?????3+????4
?
运用完全平方公式计算:
(1)1022 (2)1992
(3)4982 (4)79.82
解:(1)1022 = (100+2)2
= 1002+2×100×2+22
= 10000+400+4
= 10404
(2)1992 = (200-1)2 =2002-2×200×1+12
= 40000-400+1
= 39601
例2
运用完全平方公式计算:
(1)1022 (2)1992
(3)4982 (4)79.82
例2
解:(3)4982 = (500-2)2
= 5002-2×500×2+22
= 250000-2000+4 = 248004
(4)79.82 = (80-0.2)2
=802-2×80×0.2+0.22
= 6400-32+0.04
= 6368.04
例3
已知x-y=6,xy=-8,求:
(1) x2+y2的值;
(2)(x+y)2的值.
=36-16=20.
解:(1)∵x-y=6,xy=-8,
(x-y)2=x2+y2-2xy,
∴x2+y2=(x-y)2+2xy
(2)∵x2+y2=20,xy=-8,
∴(x+y)2=x2+y2+2xy
=20-16=4.
(1) (??????-????)2 与(????+????)2
?
比较下列各式之间的关系:
相等
(2) (?????-????)2 与(???? ??????)2
?
(3) (-????+ ????)2 与(?????+????)2
?
相等
相等
(1)(-2m-3n) ;
计算:
2
(2)
解:(1)原式=[-(2m+3n)]2
=(2m+3n)2
=(2m)2 +2·2m·3n+(3n)2
=4m2+12mn+9n2.
例4
如何用乘法公式求????+????+?????????
?
a+(b+c) = a+b+c;
a- (b+c) = a - b – c.
a + b + c = a + ( b + c) ;
a – b – c = a – ( b + c ) .
去括号法则:
反过来,就得到添括号法则:
添括号时,如果括号前面是正号,括到括号里的各项都不变符号;如果括号前面是负号,括到括号里的各项都改变符号(简记为“负变正不变”).
先变形
运用乘法公式计算:
(1) (x+2y-3)(x-2y+3) ; (2) (a+b+c)2.
解:
= [(a+b)+c]2
= x2-(2y-3)2
= x2-(4y2-12y+9)
= x2-4y2+12y-9.
= (a+b)2+2(a+b)c+c2
=a2+2ab+b2+2ac+2bc+c2
=a2+b2+c2+2ab+2ac+2bc.
例5
(x+2y-3)(x-2y+3)
=[x+(2y–3)][x-(2y-3)]
(1)
(2)(a+b+c)2
1.下列计算正确的是( )
A.(a+m)2=a2+m2
B.(s-t)2=s2-t2
随堂训练
C
D.(m+n)2=m2+mn+n2
2、若????+????=4,则????2+2????????+????2的值
是( )
A、8 B、16 C、2 D、4
?
B
(?2????????)
?
6、如果
8
?
5.
3.小兵计算一个二项整式的平方式时,得到
正确结果是4????2+ +25????2,但中间一项
不慎被污染了,这一项应是( )
A 10????????? B 20???????? C±10???????? D±20?????????
?
D
4.如果x2-6x+N是一个完全平方式,那么N是( )
A、11 B、9 C、-11 D、-9
B
解:(1)原式=[(x+1)+(y-z)][(x+1)-(y-z)]
=(x+1)2-(y
7.运用乘法公式计算:
(1)(x+y-z+1)(x-y+z+1);
(2)(a-b-c)2.
-z)2
=x2+2x+1-y2+2yz-z2.
(2)原式=[(a-b)-c]2
=(a-b)2-2(a-b)·c+c2
=a2+b2+c2
-2ab+2bc-2ac.
8.若a+b=5,ab=-6,求a2+b2,a2-ab+b2.
9.已知x+y=8,x-y=4,求xy.
解:∵a+b=5,ab=-6,
∴a2+b2=(a+b)2-2ab=52-2×(-6)=37;
解:∵x+y=8,∴(x+y)2=64,即x2+y2+2xy=64①.
∵x-y=4, ∴(x-y)2=16,即x2+y2-2xy=16②.
①-②,得
4xy=48,
∴xy=12.
a2-ab+b2=a2+b2-ab=37-(-6)=43.
课堂小结
(a+b)2= ,
a2+2ab+b2
(a-b)2= .
a2-2ab+b2
1.完全平方公式:
a + b + c = a + ( b + c) ;
a – b – c = a – ( b + c ) .
2.添括号法则:
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
