沪科版九年级上册数学同步练习 21.4 第2课时 利用二次函数解决桥梁等建筑问题(word版含答案)
文档属性
| 名称 | 沪科版九年级上册数学同步练习 21.4 第2课时 利用二次函数解决桥梁等建筑问题(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 341.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-25 10:33:33 | ||
图片预览


文档简介
沪科版九年级上册数学同步练习
第2课时 利用二次函数解决桥梁等建筑问题
一、选择题
1.位于中国贵州省内的射电望远镜(FAST)是目前世界上口径最大,精度最高的望远镜.根据有关资料显示,该望远镜的轴截面呈抛物线状,口径AB为500米,最低点C到口径面AB的距离是100米.若按如图2建立平面直角坐标系,则抛物线的表达式是
(
)
A.y=x2-100
B.y=-x2-100
C.y=x2
D.y=-x2
2.河北省赵县的赵州桥的桥拱是近似的抛物线形,建立如图所示的平面直角坐标系,其函数的表达式为y=-x2.当水面离桥拱顶的高度DO是4
m时,这时水面宽度AB为
(
)
A.-20
m
B.10
m
C.20
m
D.-10
m
3.如图,某工厂大门是抛物线形水泥建筑,大门底部地面宽4米,顶部距地面的高度为4.4米.现有一辆满载货物的汽车欲通过大门,其装货宽度为2.4米,该车要想通过此门,装货后的高度应小于
(
)
A.2.80米
B.2.816米
C.2.82米
D.2.826米
4.如图,图中是抛物线形拱桥,当拱顶离水面2
m时水面宽4
m.若水面下降1
m,则水面宽度为
(
)
A.2
m
B.2
m
C.
m
D.
m
5.来自湖南的民营企业以二次函数y=2x2-4x+8的图象为灵感设计了一款杯子,如图为杯子的设计稿.若AB=4,DE=3,则杯子的高CE为
(
)
A.14
B.11
C.6
D.3
6.如图,“武汉长江大桥”有一段抛物线形的拱梁,抛物线的表达式为y=ax2+bx.小强骑自行车从拱梁一端O沿直线匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶10秒时和26秒时拱梁高度相同,则小强骑自行车通过拱梁部分的桥面OC共需
(
)
A.18秒
B.36秒
C.38秒
D.46秒
二、填空题
7.某菜农搭建了一个横截面为抛物线的大棚,尺寸如图.若菜农的身高为1.8
m,在不弯腰的情况下,他在棚内的横向活动范围是
m.?
8.如图,在建立的平面直角坐标系中,抛物线的表达式为y=-x2,当涵洞水面宽AB为12米时,水面到拱桥顶点O的距离为
米.?
9.如图所示的一座拱桥,当水面宽AB为12
m时,桥洞顶部离水面4
m.已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点时的抛物线表达式是y=-(x-6)2+4,则选取点B为坐标原点时的抛物线表达式是
.?
10.一个涵洞呈抛物线形,它的截面如图所示.当水面宽AB=1.6
m时,涵洞顶点与水面的距离为2.4
m,这时水面上方离水面1.5
m处的涵洞宽?
m.?
11.一个横断面是抛物线的渡槽如图所示,根据图中所给的数据,求出水面的宽度是
m.?
12.如图,三孔桥横截面的三个孔都呈抛物线形,左右两个抛物线形是全等的.正常水位时,大孔水面宽度为20
m,顶点距水面6
m,小孔顶点距水面4.5
m.当水位上涨刚好淹没小孔时,大孔的水面宽度为
m.?
13.廊桥是我国古老的文化遗产,如图所示是某座抛物线形的廊桥示意图.已知抛物线的表达式是y=-x2+10,为保护廊桥上的通行安全,在抛物线上距水面AB高为8米的点E,F处要安装两盏警示灯,则这两盏灯的水平距离EF为
米.?
三、解答题
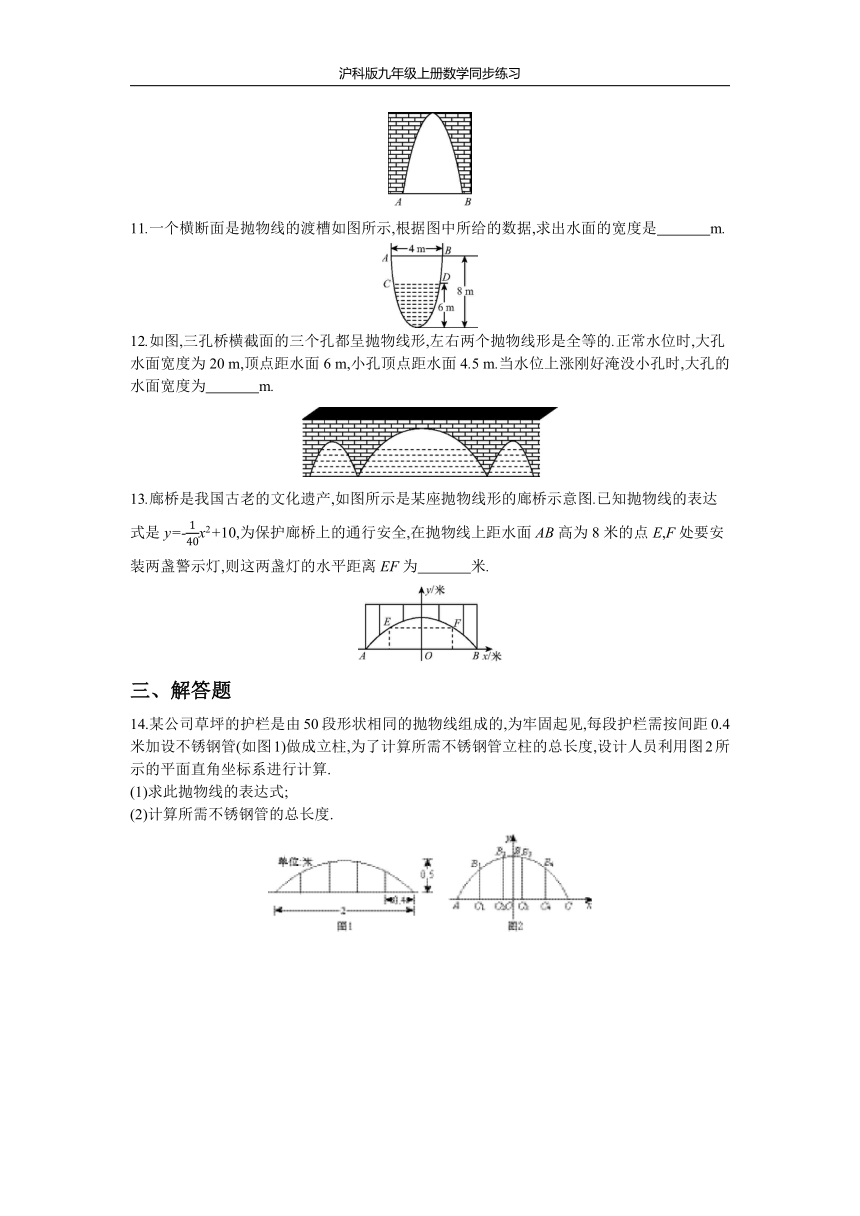
14.某公司草坪的护栏是由50段形状相同的抛物线组成的,为牢固起见,每段护栏需按间距0.4米加设不锈钢管(如图1)做成立柱,为了计算所需不锈钢管立柱的总长度,设计人员利用图2所示的平面直角坐标系进行计算.
(1)求此抛物线的表达式;
(2)计算所需不锈钢管的总长度.
15.如图所示,有一座抛物线形拱桥,桥下面的正常水位AB宽20
m,水位上升3
m就达到警戒线CD,这时水面宽度为10
m.
(1)在如图所示坐标系中求抛物线的表达式.
(2)若洪水到来时,水位以每小时0.2
m的速度上升,从警戒线开始,再持续多少小时就会到达拱桥顶?
16.某大学的校门是抛物线形水泥建筑物,大门的地面宽度为8
m,两侧距地面4
m高处各有一个挂校名横匾用的铁环,两铁环的水平距离为6
m,求校门的高.(精确到0.1
m,水泥建筑物厚度忽略不计)
17.如图所示是某隧道截面示意图,它是由抛物线和长方形构成.已知OA=12米,OB=4米,抛物线顶点D到地面OA的垂直距离为10米,以OA所在直线为x轴,以OB所在直线为y轴建立平面直角坐标系.
(1)求抛物线的表达式;
(2)由于隧道较长,需要在抛物线形拱壁上安装两排灯,使它们到地面的高度相同,如果灯离地面的高度不超过8米,那么两排灯间的水平距离最小是多少米?
参考答案
一、选择题
题号
1
2
3
4
5
6
答案
A
C
B
A
B
B
二、填空题
7. 3m
8. 18
9. y=-(x+6)2+4
10.?
11. 2
12. 10
13. 8
三、解答题
14.解:(1)设此抛物线的表达式为y=a
x2+c,
把点B(0,0.5),C(1,0)代入,得a=-0.5,c=0.5,
∴此抛物线的表达式为y=-0.5
x2+0.5.
(2)∵当x=0.2时,y=0.48;当x=0.6时,y=0.32,
∴=2×(0.48+0.32)=1.6(米),
∴所需不锈钢管的总长度为1.6×50=80(米).
15.解:(1)设所求抛物线的表达式为y=ax2,由CD=10,可设点D(5,b),由AB=20,水位上升3
m就达到警戒线CD,则点B(10,b-3).
把点D,B的坐标代入,
得解得
∴抛物线的表达式为y=-x2.
(2)∵b=-1,∴=5(小时),
∴再持续5小时就会到达拱桥顶.
16.
解:如图,以大门地面为x轴,它的中垂线为y轴建立平面直角坐标系.设抛物线的表达式为y=ax2+c,易知抛物线过(4,0),(3,4)两点,
∴解得
∴y=-x2+,∴顶点坐标为.
∵≈9.1,∴校门的高约为9.1
m.
17.解:(1)根据题意,得顶点D的坐标为(6,10),点B的坐标为(0,4),
设抛物线的表达式为y=a(x-6)2+10.把点B(0,4)代入得36a+10=4,解得a=-,
即所求抛物线的表达式为y=-(x-6)2+10.
(2)由图象可知,高度越高,两排灯间的水平距离越小,
把y=8代入y=-(x-6)2+10,得-(x-6)2+10=8,解得x1=6+2,x2=6-2,
所求最小距离为x1-x2=4(米)
第2课时 利用二次函数解决桥梁等建筑问题
一、选择题
1.位于中国贵州省内的射电望远镜(FAST)是目前世界上口径最大,精度最高的望远镜.根据有关资料显示,该望远镜的轴截面呈抛物线状,口径AB为500米,最低点C到口径面AB的距离是100米.若按如图2建立平面直角坐标系,则抛物线的表达式是
(
)
A.y=x2-100
B.y=-x2-100
C.y=x2
D.y=-x2
2.河北省赵县的赵州桥的桥拱是近似的抛物线形,建立如图所示的平面直角坐标系,其函数的表达式为y=-x2.当水面离桥拱顶的高度DO是4
m时,这时水面宽度AB为
(
)
A.-20
m
B.10
m
C.20
m
D.-10
m
3.如图,某工厂大门是抛物线形水泥建筑,大门底部地面宽4米,顶部距地面的高度为4.4米.现有一辆满载货物的汽车欲通过大门,其装货宽度为2.4米,该车要想通过此门,装货后的高度应小于
(
)
A.2.80米
B.2.816米
C.2.82米
D.2.826米
4.如图,图中是抛物线形拱桥,当拱顶离水面2
m时水面宽4
m.若水面下降1
m,则水面宽度为
(
)
A.2
m
B.2
m
C.
m
D.
m
5.来自湖南的民营企业以二次函数y=2x2-4x+8的图象为灵感设计了一款杯子,如图为杯子的设计稿.若AB=4,DE=3,则杯子的高CE为
(
)
A.14
B.11
C.6
D.3
6.如图,“武汉长江大桥”有一段抛物线形的拱梁,抛物线的表达式为y=ax2+bx.小强骑自行车从拱梁一端O沿直线匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶10秒时和26秒时拱梁高度相同,则小强骑自行车通过拱梁部分的桥面OC共需
(
)
A.18秒
B.36秒
C.38秒
D.46秒
二、填空题
7.某菜农搭建了一个横截面为抛物线的大棚,尺寸如图.若菜农的身高为1.8
m,在不弯腰的情况下,他在棚内的横向活动范围是
m.?
8.如图,在建立的平面直角坐标系中,抛物线的表达式为y=-x2,当涵洞水面宽AB为12米时,水面到拱桥顶点O的距离为
米.?
9.如图所示的一座拱桥,当水面宽AB为12
m时,桥洞顶部离水面4
m.已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点时的抛物线表达式是y=-(x-6)2+4,则选取点B为坐标原点时的抛物线表达式是
.?
10.一个涵洞呈抛物线形,它的截面如图所示.当水面宽AB=1.6
m时,涵洞顶点与水面的距离为2.4
m,这时水面上方离水面1.5
m处的涵洞宽?
m.?
11.一个横断面是抛物线的渡槽如图所示,根据图中所给的数据,求出水面的宽度是
m.?
12.如图,三孔桥横截面的三个孔都呈抛物线形,左右两个抛物线形是全等的.正常水位时,大孔水面宽度为20
m,顶点距水面6
m,小孔顶点距水面4.5
m.当水位上涨刚好淹没小孔时,大孔的水面宽度为
m.?
13.廊桥是我国古老的文化遗产,如图所示是某座抛物线形的廊桥示意图.已知抛物线的表达式是y=-x2+10,为保护廊桥上的通行安全,在抛物线上距水面AB高为8米的点E,F处要安装两盏警示灯,则这两盏灯的水平距离EF为
米.?
三、解答题
14.某公司草坪的护栏是由50段形状相同的抛物线组成的,为牢固起见,每段护栏需按间距0.4米加设不锈钢管(如图1)做成立柱,为了计算所需不锈钢管立柱的总长度,设计人员利用图2所示的平面直角坐标系进行计算.
(1)求此抛物线的表达式;
(2)计算所需不锈钢管的总长度.
15.如图所示,有一座抛物线形拱桥,桥下面的正常水位AB宽20
m,水位上升3
m就达到警戒线CD,这时水面宽度为10
m.
(1)在如图所示坐标系中求抛物线的表达式.
(2)若洪水到来时,水位以每小时0.2
m的速度上升,从警戒线开始,再持续多少小时就会到达拱桥顶?
16.某大学的校门是抛物线形水泥建筑物,大门的地面宽度为8
m,两侧距地面4
m高处各有一个挂校名横匾用的铁环,两铁环的水平距离为6
m,求校门的高.(精确到0.1
m,水泥建筑物厚度忽略不计)
17.如图所示是某隧道截面示意图,它是由抛物线和长方形构成.已知OA=12米,OB=4米,抛物线顶点D到地面OA的垂直距离为10米,以OA所在直线为x轴,以OB所在直线为y轴建立平面直角坐标系.
(1)求抛物线的表达式;
(2)由于隧道较长,需要在抛物线形拱壁上安装两排灯,使它们到地面的高度相同,如果灯离地面的高度不超过8米,那么两排灯间的水平距离最小是多少米?
参考答案
一、选择题
题号
1
2
3
4
5
6
答案
A
C
B
A
B
B
二、填空题
7. 3m
8. 18
9. y=-(x+6)2+4
10.?
11. 2
12. 10
13. 8
三、解答题
14.解:(1)设此抛物线的表达式为y=a
x2+c,
把点B(0,0.5),C(1,0)代入,得a=-0.5,c=0.5,
∴此抛物线的表达式为y=-0.5
x2+0.5.
(2)∵当x=0.2时,y=0.48;当x=0.6时,y=0.32,
∴=2×(0.48+0.32)=1.6(米),
∴所需不锈钢管的总长度为1.6×50=80(米).
15.解:(1)设所求抛物线的表达式为y=ax2,由CD=10,可设点D(5,b),由AB=20,水位上升3
m就达到警戒线CD,则点B(10,b-3).
把点D,B的坐标代入,
得解得
∴抛物线的表达式为y=-x2.
(2)∵b=-1,∴=5(小时),
∴再持续5小时就会到达拱桥顶.
16.
解:如图,以大门地面为x轴,它的中垂线为y轴建立平面直角坐标系.设抛物线的表达式为y=ax2+c,易知抛物线过(4,0),(3,4)两点,
∴解得
∴y=-x2+,∴顶点坐标为.
∵≈9.1,∴校门的高约为9.1
m.
17.解:(1)根据题意,得顶点D的坐标为(6,10),点B的坐标为(0,4),
设抛物线的表达式为y=a(x-6)2+10.把点B(0,4)代入得36a+10=4,解得a=-,
即所求抛物线的表达式为y=-(x-6)2+10.
(2)由图象可知,高度越高,两排灯间的水平距离越小,
把y=8代入y=-(x-6)2+10,得-(x-6)2+10=8,解得x1=6+2,x2=6-2,
所求最小距离为x1-x2=4(米)
