沪科版九年级上册数学同步练习 22.1 第3课时 平行线分线段成比例定理及推论(Word版 含答案)
文档属性
| 名称 | 沪科版九年级上册数学同步练习 22.1 第3课时 平行线分线段成比例定理及推论(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 224.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-25 10:48:51 | ||
图片预览

文档简介
沪科版九年级上册数学同步练习
第3课时 平行线分线段成比例定理及推论
一、选择题
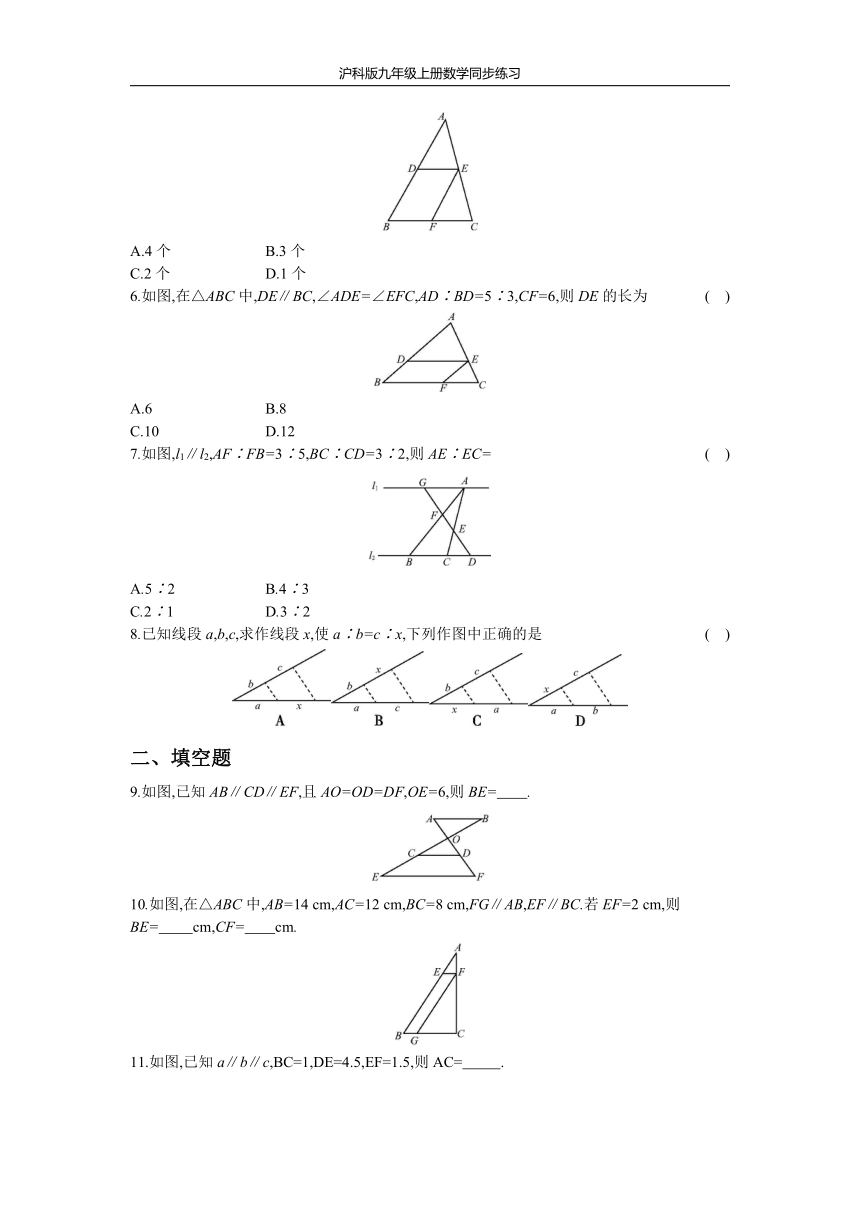
1.如图,已知AB∥CD∥EF,那么下列结论正确的是
(
)
A.=
B.=
C.=
D.=
2.如图,已知在△ABC中,点D,E,F分别是边AB,AC,BC上的点,
DE∥BC
,
AB∥EF,且AD∶DB=3∶5,那么CF∶CB等于
(
)
A.5∶8
B.3∶8
C.3∶5
D.2∶5
3.如图,AB∥CD∥EF,BD∶DF=3∶5,那么下列结论正确的是
(
)
A.
B.
C.
D.
4.如图,在△ABC中,DE∥BC,,AE=2,则EC的长是
(
)
A.1
B.4
C.6
D.8
5.如图,已知DE∥BC,EF∥AB,现得到下列结论:
①;②;③;④.
其中正确的结论有
(
)
A.4个
B.3个
C.2个
D.1个
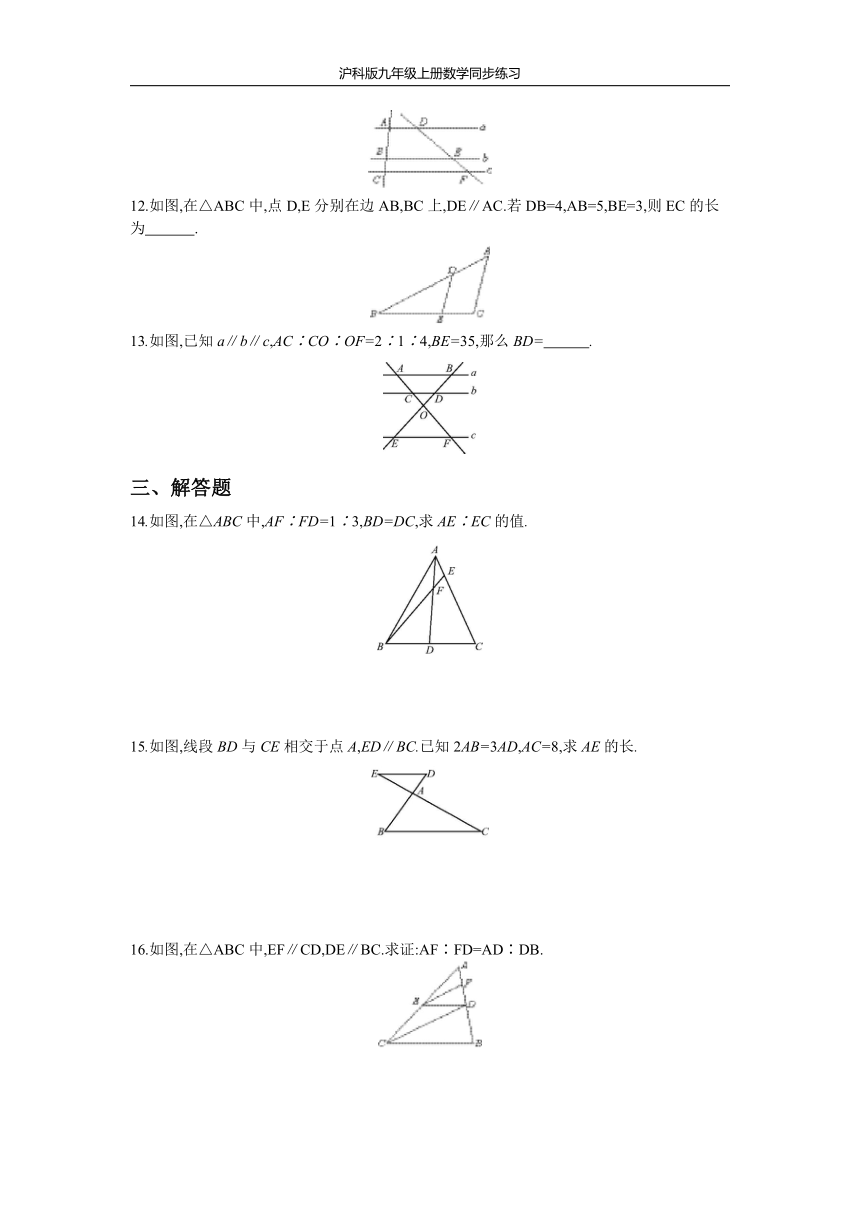
6.如图,在△ABC中,DE∥BC,∠ADE=∠EFC,AD∶BD=5∶3,CF=6,则DE的长为
(
)
A.6
B.8
C.10
D.12
7.如图,l1∥l2,AF∶FB=3∶5,BC∶CD=3∶2,则AE∶EC=
(
)
A.5∶2
B.4∶3
C.2∶1
D.3∶2
8.已知线段a,b,c,求作线段x,使a∶b=c∶x,下列作图中正确的是
(
)
二、填空题
9.如图,已知AB∥CD∥EF,且AO=OD=DF,OE=6,则BE= .?
10.如图,在△ABC中,AB=14
cm,AC=12
cm,BC=8
cm,FG∥AB,EF∥BC.若EF=2
cm,则BE=?
cm,CF= cm.?
11.如图,已知a∥b∥c,BC=1,DE=4.5,EF=1.5,则AC=
.?
12.如图,在△ABC中,点D,E分别在边AB,BC上,DE∥AC.若DB=4,AB=5,BE=3,则EC的长为?
.?
13.如图,已知a∥b∥c,AC∶CO∶OF=2∶1∶4,BE=35,那么BD=
.?
三、解答题
14.如图,在△ABC中,AF∶FD=1∶3,BD=DC,求AE∶EC的值.
15.如图,线段BD与CE相交于点A,ED∥BC.已知2AB=3AD,AC=8,求AE的长.
16.如图,在△ABC中,EF∥CD,DE∥BC.求证:AF∶FD=AD∶DB.
17.如图,已知AD∥BE∥CF,它们依次交直线l1,l2于点A,B,C和点D,E,F.
(1)如果AB=6,BC=8,DF=21,求DE的长;
(2)如果DE∶DF=2∶5,AD=9,CF=14,求BE的长.
18.阅读下面的材料,并回答所提出的问题.三角形内角平分线性质定理:三角形的内角平分线分对边所得的两条线段和这个角的两边对应成比例.
已知:在△ABC中,AD是角平分线.
求证:.
参考答案
一、选择题
题号
1
2
3
4
5
6
7
8
答案
A
A
C
B
B
C
D
B
二、填空题
9. 9
10.
9
11. 4
12.?
13. 10
三、解答题
14.解:过点D作DG∥BE,交AC于点G,
则AF∶FD=AE∶EG=1∶3,BD∶CD=EG∶CG=1∶1,
所以AE∶EC=1∶6.
15.解:AE=.
16.证明:∵EF∥CD,DE∥BC,∴=,=,
∴=,即AF∶FD=AD∶DB.
17.解:(1)∵AD∥BE∥CF,∴,
∵AB=6,BC=8,DF=21,∴,
∴DE=9.
(2)过点D作DG∥AC,交BE于点H,交CF于点G,
∴CG=BH=AD=9,∴GF=14-9=5.
∵HE∥GF,∴.
∵DE∶DF=2∶5,GF=5,∴,∴HE=2,
∴BE=9+2=11.
18.证明:如图1,过点C作CE∥DA,交BA的延长线于点E.
∵CE∥DA,∴∠2=∠3,∠1=∠E.
又∵AD平分∠BAC,∴∠1=∠2,
∴∠3=∠E,∴AC=AE.
∵CE∥DA,∴.
又∵AC=AE,∴.
用三角形内角平分线性质定理解答下面的问题:如图2,在△ABC中,AD是角平分线,AB=5
cm,AC=4
cm,BC=7
cm,求BD的长.
解:∵AD是角平分线,∴.
又∵AB=5
cm,AC=4
cm,BC=7
cm,
∴,∴BD=
cm.
第3课时 平行线分线段成比例定理及推论
一、选择题
1.如图,已知AB∥CD∥EF,那么下列结论正确的是
(
)
A.=
B.=
C.=
D.=
2.如图,已知在△ABC中,点D,E,F分别是边AB,AC,BC上的点,
DE∥BC
,
AB∥EF,且AD∶DB=3∶5,那么CF∶CB等于
(
)
A.5∶8
B.3∶8
C.3∶5
D.2∶5
3.如图,AB∥CD∥EF,BD∶DF=3∶5,那么下列结论正确的是
(
)
A.
B.
C.
D.
4.如图,在△ABC中,DE∥BC,,AE=2,则EC的长是
(
)
A.1
B.4
C.6
D.8
5.如图,已知DE∥BC,EF∥AB,现得到下列结论:
①;②;③;④.
其中正确的结论有
(
)
A.4个
B.3个
C.2个
D.1个
6.如图,在△ABC中,DE∥BC,∠ADE=∠EFC,AD∶BD=5∶3,CF=6,则DE的长为
(
)
A.6
B.8
C.10
D.12
7.如图,l1∥l2,AF∶FB=3∶5,BC∶CD=3∶2,则AE∶EC=
(
)
A.5∶2
B.4∶3
C.2∶1
D.3∶2
8.已知线段a,b,c,求作线段x,使a∶b=c∶x,下列作图中正确的是
(
)
二、填空题
9.如图,已知AB∥CD∥EF,且AO=OD=DF,OE=6,则BE= .?
10.如图,在△ABC中,AB=14
cm,AC=12
cm,BC=8
cm,FG∥AB,EF∥BC.若EF=2
cm,则BE=?
cm,CF= cm.?
11.如图,已知a∥b∥c,BC=1,DE=4.5,EF=1.5,则AC=
.?
12.如图,在△ABC中,点D,E分别在边AB,BC上,DE∥AC.若DB=4,AB=5,BE=3,则EC的长为?
.?
13.如图,已知a∥b∥c,AC∶CO∶OF=2∶1∶4,BE=35,那么BD=
.?
三、解答题
14.如图,在△ABC中,AF∶FD=1∶3,BD=DC,求AE∶EC的值.
15.如图,线段BD与CE相交于点A,ED∥BC.已知2AB=3AD,AC=8,求AE的长.
16.如图,在△ABC中,EF∥CD,DE∥BC.求证:AF∶FD=AD∶DB.
17.如图,已知AD∥BE∥CF,它们依次交直线l1,l2于点A,B,C和点D,E,F.
(1)如果AB=6,BC=8,DF=21,求DE的长;
(2)如果DE∶DF=2∶5,AD=9,CF=14,求BE的长.
18.阅读下面的材料,并回答所提出的问题.三角形内角平分线性质定理:三角形的内角平分线分对边所得的两条线段和这个角的两边对应成比例.
已知:在△ABC中,AD是角平分线.
求证:.
参考答案
一、选择题
题号
1
2
3
4
5
6
7
8
答案
A
A
C
B
B
C
D
B
二、填空题
9. 9
10.
9
11. 4
12.?
13. 10
三、解答题
14.解:过点D作DG∥BE,交AC于点G,
则AF∶FD=AE∶EG=1∶3,BD∶CD=EG∶CG=1∶1,
所以AE∶EC=1∶6.
15.解:AE=.
16.证明:∵EF∥CD,DE∥BC,∴=,=,
∴=,即AF∶FD=AD∶DB.
17.解:(1)∵AD∥BE∥CF,∴,
∵AB=6,BC=8,DF=21,∴,
∴DE=9.
(2)过点D作DG∥AC,交BE于点H,交CF于点G,
∴CG=BH=AD=9,∴GF=14-9=5.
∵HE∥GF,∴.
∵DE∶DF=2∶5,GF=5,∴,∴HE=2,
∴BE=9+2=11.
18.证明:如图1,过点C作CE∥DA,交BA的延长线于点E.
∵CE∥DA,∴∠2=∠3,∠1=∠E.
又∵AD平分∠BAC,∴∠1=∠2,
∴∠3=∠E,∴AC=AE.
∵CE∥DA,∴.
又∵AC=AE,∴.
用三角形内角平分线性质定理解答下面的问题:如图2,在△ABC中,AD是角平分线,AB=5
cm,AC=4
cm,BC=7
cm,求BD的长.
解:∵AD是角平分线,∴.
又∵AB=5
cm,AC=4
cm,BC=7
cm,
∴,∴BD=
cm.
