沪科版九年级上册数学同步练习 22.2 第4课时 三角形相似的判定定理3(Word版 含答案)
文档属性
| 名称 | 沪科版九年级上册数学同步练习 22.2 第4课时 三角形相似的判定定理3(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 335.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-25 00:00:00 | ||
图片预览


文档简介
沪科版九年级上册数学同步练习
第4课时 三角形相似的判定定理3
一、选择题
1.有甲、乙两个三角形木框,甲三角形木框的三边长分别为1,,,乙三角形木框的三边长分别为5,,,则甲、乙两个三角形
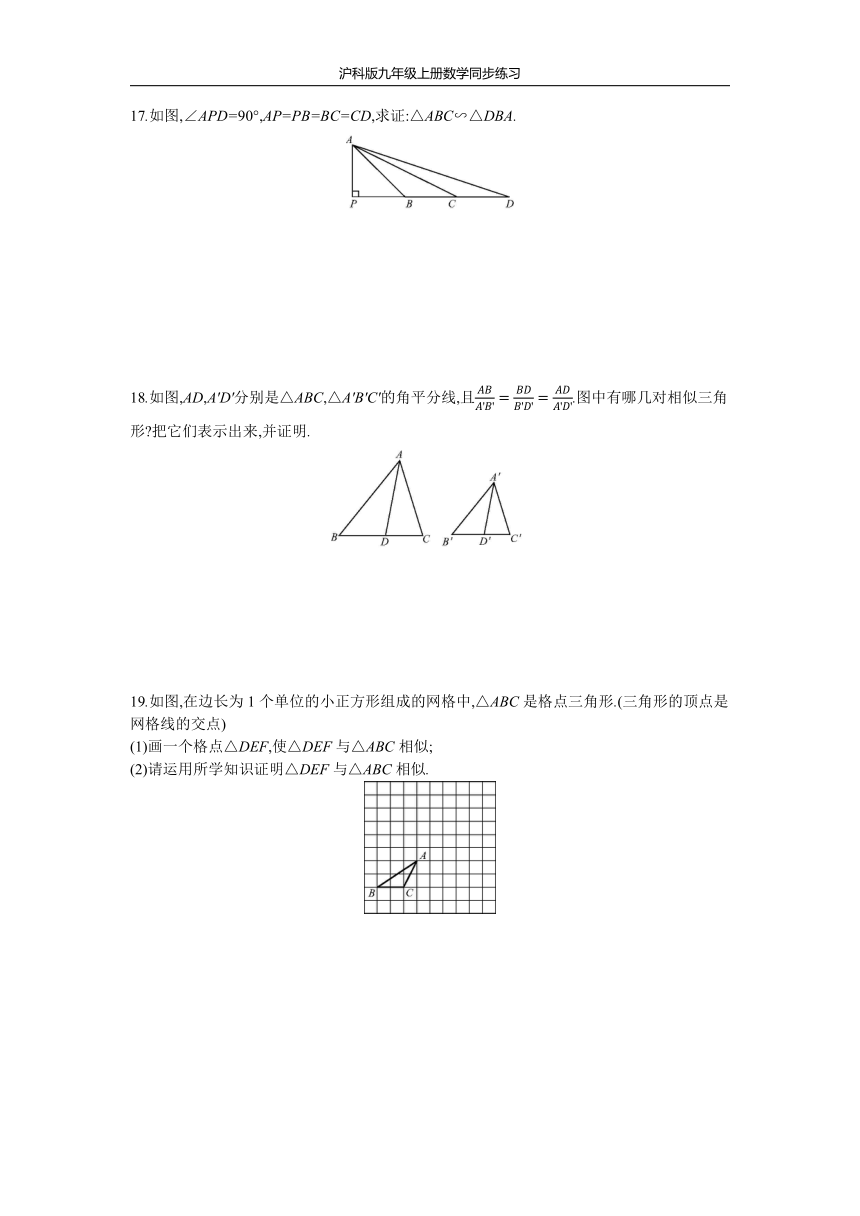
(
)
A.一定相似
B.一定不相似
C.不一定相似
D.无法判断
2.已知△ABC的三边长分别为6
cm,7.5
cm,9
cm,△DEF的一边长为4
cm.当这两个三角形相似时,△DEF的另两边长可以是
(
)
A.2
cm,3
cm
B.4
cm,5
cm
C.5
cm,6
cm
D.6
cm,7
cm
3.下列四个三角形中,与所给图中的三角形相似的是
(
)
4.如图,网格线是由相同的小正方形拼成的,有四个三角形①②③④.其中相似的三角形是(
)
A.①与②
B.②与④
C.①与③
D.③与④
5.已知△ABC的三边长分别为7.5,9和10.5,△DEF的一边长为5.当△DEF的另两边长是下列哪一组时,这两个三角形相似
(
)
A.4,5
B.5,6
C.6,7
D.7,8
6.下列各组三角形中,两个三角形一定相似的是
(
)
A.△ABC中,∠A=42°,∠B=118°,△A'B'C'中,∠A'=118°,∠B'=15°
B.△ABC中,AB=8,AC=4,∠A=105°,△A'B'C'中,A'B'=16,B'C'=8,∠A'=100°
C.△ABC中,AB=18,BC=20,CA=35,△A'B'C'中,A'B'=36,B'C'=40,C'A'=70
D.△ABC和△A'B'C'中,有,∠C=∠C'
7.如图,O为△ABC内一点,D,E,F分别是OA,OB,OC的中点,则图中相似三角形共有
(
)
A.2对
B.3对
C.4对
D.5对
8.如图,小正方形的边长均为1,则图中三角形(阴影部分)与△ABC相似的是
(
)
9.如图,△PQR在边长为1的小正方形组成的方格纸中,它的顶点在小正方形的顶点上,其中点A,B,C,D也是小正方形的顶点,那么下列三角形中,与△PQR相似的是
(
)
A.以点P,Q,A为顶点的三角形
B.以点P,Q,B为顶点的三角形
C.以点P,Q,C为顶点的三角形
D.以点P,Q,D为顶点的三角形
二、填空题
10.已知在△ABC中,AB=12
cm,AC=15
cm,BC=21
cm;在中,=16
cm,=28
cm.则当= cm时,△ABC∽.?
11.在△ABC中,已知AB=4,BC=5,AC=6.如果DE=10,那么当EF=?
,FD=
时,△DEF∽△ABC.?
12.在△ABC和△DEF中,如果AB=4,BC=3,AC=6,DE=2.4,EF=1.2,FD=1.6.那么这两个三角形 相
(填“相似”或“不相似”),理由是
.?
13.如图,点D在△ABC内,连接BD并延长到点E,连接AD,AE.若,且∠CAE=29°,则∠BAD=
.?
14.在△ABC中,AB∶BC∶CA=2∶3∶4,在△A'B'C'中,A'B'=1,C'A'=2.当B'C'=
时,△ABC∽△A'B'C'.?
15.在△ABC中,AB∶BC∶CA=3∶5∶7.在△DEF中,若DE=6
cm,且EF三、解答题
16.如图,在△ABC中,AB=25,BC=40,AC=20.在△ADE中,AE=12,AD=15,DE=24,试判断这两个三角形是否相似?并说明理由.
17.如图,∠APD=90°,AP=PB=BC=CD,求证:△ABC∽△DBA.
18.如图,AD,A'D'分别是△ABC,△A'B'C'的角平分线,且.图中有哪几对相似三角形?把它们表示出来,并证明.
19.如图,在边长为1个单位的小正方形组成的网格中,△ABC是格点三角形.(三角形的顶点是网格线的交点)
(1)画一个格点△DEF,使△DEF与△ABC相似;
(2)请运用所学知识证明△DEF与△ABC相似.
20.如图1,点O在△ABC内部,连接AO,BO,CO,点A',B',C'分别在AO,BO,CO上,且AB∥A'B',BC∥B'C'.
(1)求证:△ABC∽△A'B'C'.
(2)将点O移至△ABC外,如图2,补充图形.若其他条件不变,题中要求证的结论还成立吗?如果成立,请换一种判定方法证明结论.
参考答案
一、选择题
题号
1
2
3
4
5
6
7
8
9
答案
A
C
B
D
C
C
C
B
B
二、填空题
10. 20
11.? 15
12. 相似 三边成比例的两个三角形相似
13. 29°
14. 1.5
15. 3∶5或3∶7或5∶7
【提示】本题由于相似三角形的对应边没有唯一确定,所以分三种情况,DE可能对应AB,也可能对应BC,也可能对应CA.又因为EF三、解答题
16.解:相似.
理由:∵==,==,==,
∴==,∴△ABC∽△ADE.
17.证明:方法1:∵∠APD=90°,设AP=PB=BC=CD=a,∴AB=a,AC=a,AD=a,BD=2a.∵,∴,∴△ABC∽△DBA.
方法2:∵∠APD=90°,AP=PB=BC=CD=a,
∴AB=a,AC=a,AD=a,BD=2a.
∵,∴.
∵∠ABC=∠DBA,∴△ABC∽△DBA.
18.解:∵,∴△ABD∽△A'B'D',
∴∠B=∠B',∠BAD=∠B'A'D'.
∵AD,A'D'分别是△ABC,△A'B'C'的角平分线,
∴∠BAC=∠B'A'C'=2∠BAD,
∴△ABC∽△A'B'C',∴∠C=∠C'.
又∵∠CAD=∠C'A'D'=∠BAC,
∴△CAD∽△C'A'D'.
综上所述,图中的相似三角形有3对:△ABD∽△A'B'D',△ABC∽△A'B'C',△CAD∽△C'A'D'.
19.解:(1)如图.(本题答案不唯一)
(2)由勾股定理得AB=,AC=,DE=2,DF=2.
又因为BC=2,EF=4,所以,所以△ABC∽△DEF.
20.证明:(1)∵AB∥A'B',BC∥B'C',
∴△OA'B'∽△OAB,△OB'C'∽△OBC,∠A'B'C'=∠ABC,∴,
∴△A'B'C'∽△ABC.
(2)补充图形如图所示,(1)中的结论仍成立,证明如下:
∵AB∥A'B',BC∥B'C',
∴,且∠A'OC'=∠AOC,
∴△OA'C'∽△OAC,∴A'C'∥AC.
根据平行线的性质,得∠ABC=∠A'B'C',∠BAC=∠B'A'C',∠ACB=A'C'B',
∴△A'B'C'∽△ABC.
第4课时 三角形相似的判定定理3
一、选择题
1.有甲、乙两个三角形木框,甲三角形木框的三边长分别为1,,,乙三角形木框的三边长分别为5,,,则甲、乙两个三角形
(
)
A.一定相似
B.一定不相似
C.不一定相似
D.无法判断
2.已知△ABC的三边长分别为6
cm,7.5
cm,9
cm,△DEF的一边长为4
cm.当这两个三角形相似时,△DEF的另两边长可以是
(
)
A.2
cm,3
cm
B.4
cm,5
cm
C.5
cm,6
cm
D.6
cm,7
cm
3.下列四个三角形中,与所给图中的三角形相似的是
(
)
4.如图,网格线是由相同的小正方形拼成的,有四个三角形①②③④.其中相似的三角形是(
)
A.①与②
B.②与④
C.①与③
D.③与④
5.已知△ABC的三边长分别为7.5,9和10.5,△DEF的一边长为5.当△DEF的另两边长是下列哪一组时,这两个三角形相似
(
)
A.4,5
B.5,6
C.6,7
D.7,8
6.下列各组三角形中,两个三角形一定相似的是
(
)
A.△ABC中,∠A=42°,∠B=118°,△A'B'C'中,∠A'=118°,∠B'=15°
B.△ABC中,AB=8,AC=4,∠A=105°,△A'B'C'中,A'B'=16,B'C'=8,∠A'=100°
C.△ABC中,AB=18,BC=20,CA=35,△A'B'C'中,A'B'=36,B'C'=40,C'A'=70
D.△ABC和△A'B'C'中,有,∠C=∠C'
7.如图,O为△ABC内一点,D,E,F分别是OA,OB,OC的中点,则图中相似三角形共有
(
)
A.2对
B.3对
C.4对
D.5对
8.如图,小正方形的边长均为1,则图中三角形(阴影部分)与△ABC相似的是
(
)
9.如图,△PQR在边长为1的小正方形组成的方格纸中,它的顶点在小正方形的顶点上,其中点A,B,C,D也是小正方形的顶点,那么下列三角形中,与△PQR相似的是
(
)
A.以点P,Q,A为顶点的三角形
B.以点P,Q,B为顶点的三角形
C.以点P,Q,C为顶点的三角形
D.以点P,Q,D为顶点的三角形
二、填空题
10.已知在△ABC中,AB=12
cm,AC=15
cm,BC=21
cm;在中,=16
cm,=28
cm.则当= cm时,△ABC∽.?
11.在△ABC中,已知AB=4,BC=5,AC=6.如果DE=10,那么当EF=?
,FD=
时,△DEF∽△ABC.?
12.在△ABC和△DEF中,如果AB=4,BC=3,AC=6,DE=2.4,EF=1.2,FD=1.6.那么这两个三角形 相
(填“相似”或“不相似”),理由是
.?
13.如图,点D在△ABC内,连接BD并延长到点E,连接AD,AE.若,且∠CAE=29°,则∠BAD=
.?
14.在△ABC中,AB∶BC∶CA=2∶3∶4,在△A'B'C'中,A'B'=1,C'A'=2.当B'C'=
时,△ABC∽△A'B'C'.?
15.在△ABC中,AB∶BC∶CA=3∶5∶7.在△DEF中,若DE=6
cm,且EF
16.如图,在△ABC中,AB=25,BC=40,AC=20.在△ADE中,AE=12,AD=15,DE=24,试判断这两个三角形是否相似?并说明理由.
17.如图,∠APD=90°,AP=PB=BC=CD,求证:△ABC∽△DBA.
18.如图,AD,A'D'分别是△ABC,△A'B'C'的角平分线,且.图中有哪几对相似三角形?把它们表示出来,并证明.
19.如图,在边长为1个单位的小正方形组成的网格中,△ABC是格点三角形.(三角形的顶点是网格线的交点)
(1)画一个格点△DEF,使△DEF与△ABC相似;
(2)请运用所学知识证明△DEF与△ABC相似.
20.如图1,点O在△ABC内部,连接AO,BO,CO,点A',B',C'分别在AO,BO,CO上,且AB∥A'B',BC∥B'C'.
(1)求证:△ABC∽△A'B'C'.
(2)将点O移至△ABC外,如图2,补充图形.若其他条件不变,题中要求证的结论还成立吗?如果成立,请换一种判定方法证明结论.
参考答案
一、选择题
题号
1
2
3
4
5
6
7
8
9
答案
A
C
B
D
C
C
C
B
B
二、填空题
10. 20
11.? 15
12. 相似 三边成比例的两个三角形相似
13. 29°
14. 1.5
15. 3∶5或3∶7或5∶7
【提示】本题由于相似三角形的对应边没有唯一确定,所以分三种情况,DE可能对应AB,也可能对应BC,也可能对应CA.又因为EF
16.解:相似.
理由:∵==,==,==,
∴==,∴△ABC∽△ADE.
17.证明:方法1:∵∠APD=90°,设AP=PB=BC=CD=a,∴AB=a,AC=a,AD=a,BD=2a.∵,∴,∴△ABC∽△DBA.
方法2:∵∠APD=90°,AP=PB=BC=CD=a,
∴AB=a,AC=a,AD=a,BD=2a.
∵,∴.
∵∠ABC=∠DBA,∴△ABC∽△DBA.
18.解:∵,∴△ABD∽△A'B'D',
∴∠B=∠B',∠BAD=∠B'A'D'.
∵AD,A'D'分别是△ABC,△A'B'C'的角平分线,
∴∠BAC=∠B'A'C'=2∠BAD,
∴△ABC∽△A'B'C',∴∠C=∠C'.
又∵∠CAD=∠C'A'D'=∠BAC,
∴△CAD∽△C'A'D'.
综上所述,图中的相似三角形有3对:△ABD∽△A'B'D',△ABC∽△A'B'C',△CAD∽△C'A'D'.
19.解:(1)如图.(本题答案不唯一)
(2)由勾股定理得AB=,AC=,DE=2,DF=2.
又因为BC=2,EF=4,所以,所以△ABC∽△DEF.
20.证明:(1)∵AB∥A'B',BC∥B'C',
∴△OA'B'∽△OAB,△OB'C'∽△OBC,∠A'B'C'=∠ABC,∴,
∴△A'B'C'∽△ABC.
(2)补充图形如图所示,(1)中的结论仍成立,证明如下:
∵AB∥A'B',BC∥B'C',
∴,且∠A'OC'=∠AOC,
∴△OA'C'∽△OAC,∴A'C'∥AC.
根据平行线的性质,得∠ABC=∠A'B'C',∠BAC=∠B'A'C',∠ACB=A'C'B',
∴△A'B'C'∽△ABC.
