沪科版九年级上册数学同步练习 22.3 第2课时 相似三角形的性质定理2,3及应用(Word版 含答案)
文档属性
| 名称 | 沪科版九年级上册数学同步练习 22.3 第2课时 相似三角形的性质定理2,3及应用(Word版 含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 187.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-25 10:41:30 | ||
图片预览


文档简介
沪科版九年级上册数学同步练习
第2课时 相似三角形的性质定理2,3及应用
一、选择题
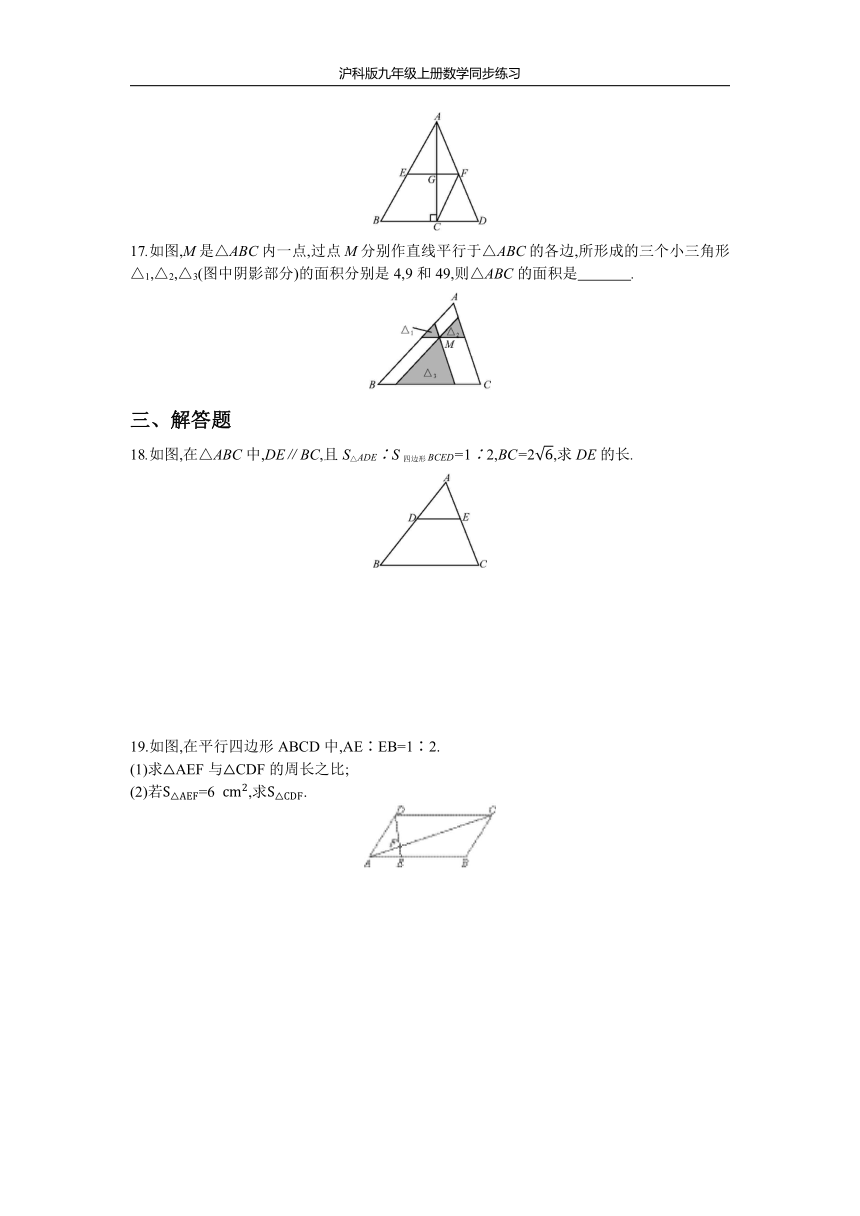
1.如图,在平行四边形ABCD中,E是AD边上的中点,连接BE并延长,交CD的延长线于点F,则△EDF与△BCF的周长之比是
(
)
A.1∶2
B.1∶3
C.1∶4
D.1∶5
2.如图,D,E分别是△ABC的边AB,AC的中点.如果△ADE的周长是6,则△ABC的周长是
(
)
A.6
B.12
C.18
D.24
3.若△ABC与△DEF的相似比为1∶4,则△ABC与△DEF的周长比为
(
)
A.1∶2
B.1∶3
C.1∶4
D.1∶16
4.已知△ABC∽△DEF,且△ABC与△DEF的面积比为9∶4,△ABC的最短边为4.5
cm,则△DEF的最短边为
(
)
A.6
cm
B.2
cm
C.3
cm
D.4
cm
5.如图,△ABC是等边三角形,它被一个平行于BC的矩形所截,AB被截成三等份,则图中阴影部分的面积是△ABC的面积的
(
)
A.
B.
C.
D.
6.若△ABC与△DEF相似,且相似比为3,△ABC的周长为18,则△DEF的周长为
(
)
A.54
B.6
C.3
D.2
7.如图,圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影(圆形).已知桌面的直径为1.2米,桌面距地面1米.若灯泡距离地面3米,则地面上阴影部分的面积为
(
)
A.0.36π平方米
B.0.81π平方米
C.2π平方米
D.3.24π平方米
8.如图,△ABC的面积是12,D,E,F,G分别是BC,AD,BE,CE的中点,则△AFG的面积是
(
)
A.4.5
B.5
C.5.5
D.6
9.如图,在一块斜边长30
cm的直角三角形木板(Rt△ACB)上截取一个正方形CDEF,点D在边BC上,点E在斜边AB上,点F在边AC上.若AF∶AC=1∶3,则这块木板截取正方形CDEF后,剩余部分的面积为
(
)
A.100
cm2
B.150
cm2
C.170
cm2
D.200
cm2
10.如图,在矩形ABCD中,E是CD边的中点,且BE⊥AC于点F,连接DF,则下列结论错误的是(
)
A.△ADC∽△CFB
B.AD=DF
C.
D.
二、填空题
11.已知△ABC∽△DEF,其中AB=6,BC=8,AC=12,DE=3,那么△DEF的周长为
.?
12.如图,在△ABC中,点D,E分别在AB,AC上,∠AED=∠B.若AE=2,△ADE的面积为4,四边形BCED的面积为5,则AB的长为
.?
13.如果两个相似三角形对应角平分线的比是4∶9,那么它们的周长比是
.?
14.已知△ABC∽△A'B'C',它们的相似比为7∶9,若△ABC的周长为56
cm,那么△A'B'C'的周长为
.?
15.如果两个相似三角形的相似比是2∶3,较小三角形的面积为4
cm2,那么较大三角形的面积为
cm2.?
16.如图,在△ABD中,∠ACB=90°,直线EF∥BD,交AB于点E,交AC于点G,交AD于点F.若S△AEG=S四边形EBCG,则=?
.?
17.如图,M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1,△2,△3(图中阴影部分)的面积分别是4,9和49,则△ABC的面积是
.?
三、解答题
18.如图,在△ABC中,DE∥BC,且S△ADE∶S四边形BCED=1∶2,BC=2,求DE的长.
19.如图,在平行四边形ABCD中,AE∶EB=1∶2.
(1)求△AEF与△CDF的周长之比;
(2)若=6
,求.
20.如图,已知AC∥BD,AB和CD相交于点E,AC=6,BD=4,F是BC上一点,且S△BEF∶S△EFC=2∶3.
(1)求EF的长;
(2)如果△BEF的面积为4,求△ABC的面积.
21.已知△ABC∽△A'B'C',,AB边上的中线CD=4
cm,△ABC的周长为20
cm,△A'B'C'的面积为64
cm2.
(1)求A'B'边上的中线C'D'的长;
(2)求△A'B'C'的周长;
(3)求△ABC的面积.
22.如图,D,E分别是△ABC的边BC,AB上的点,△ABC,△BDE,△ACD的周长依次为m,m1,m2.
(1)当∠2=∠3,BD=BC时,求的值;
(2)当∠1=∠2,BD=BC时,求的值.
参考答案
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
答案
A
B
C
C
C
B
B
A
A
C
二、填空题
11. 13
12. 3
13. 4∶9
14. 72
cm
15. 9
16.?
17. 144
【提示】如图,易得△DEM∽△MPQ∽△FMG∽△ABC,∴EM∶MG∶PQ=2∶3∶7,∴EM∶BC=2∶12=1∶6,∴S△ABC=36×4=144.
三、解答题
18.解:DE=2.
19.解:(1)因为四边形ABCD是平行四边形,
所以AB=CD,AB∥CD,所以△AEF∽△CDF.
因为AE∶EB=1∶2,所以AE∶AB=AE∶CD=1∶3,
所以△AEF与△CDF的周长之比为1∶3.
(2)由(1)知,△AEF∽△CDF,相似比为1∶3,
所以它们的面积之比为1∶9.
因为=6
,所以=54
.
20.解:(1)∵AC∥BD,∴.
∵△BEF和△EFC同高,且S△BEF∶S△EFC=2∶3,
∴,∴,即,
∴△BEF∽△BAC,∴,
∴EF=×6=.
(2)∵△BEF∽△BAC,∴,
∴S△ABC=25.
21.解:(1)∵△ABC∽△A'B'C',,AB边上的中线CD=4
cm,∴,∴C'D'=4×2=8(cm),
即A'B'边上的中线C'D'的长为8
cm.
(2)∵△ABC∽△A'B'C',,△ABC的周长为20
cm,
∴,∴C△A'B'C'=20×2=40(cm),
∴△A'B'C'的周长为40
cm.
(3)∵△ABC∽△A'B'C',,△A'B'C'的面积为64
cm2,∴,
∴S△ABC=64÷4=16(cm2),即△ABC的面积为16
cm2.
22.解:(1)∵∠2=∠3,∴DE∥AC,
∴△BDE∽△BCA,∴,
由BD=BC,得,即.
(2)∵∠1=∠2,∠C是公共角,
∴△ACD∽△BCA,∴,
∴.
由BD=BC,得DC=BC,
∴.
第2课时 相似三角形的性质定理2,3及应用
一、选择题
1.如图,在平行四边形ABCD中,E是AD边上的中点,连接BE并延长,交CD的延长线于点F,则△EDF与△BCF的周长之比是
(
)
A.1∶2
B.1∶3
C.1∶4
D.1∶5
2.如图,D,E分别是△ABC的边AB,AC的中点.如果△ADE的周长是6,则△ABC的周长是
(
)
A.6
B.12
C.18
D.24
3.若△ABC与△DEF的相似比为1∶4,则△ABC与△DEF的周长比为
(
)
A.1∶2
B.1∶3
C.1∶4
D.1∶16
4.已知△ABC∽△DEF,且△ABC与△DEF的面积比为9∶4,△ABC的最短边为4.5
cm,则△DEF的最短边为
(
)
A.6
cm
B.2
cm
C.3
cm
D.4
cm
5.如图,△ABC是等边三角形,它被一个平行于BC的矩形所截,AB被截成三等份,则图中阴影部分的面积是△ABC的面积的
(
)
A.
B.
C.
D.
6.若△ABC与△DEF相似,且相似比为3,△ABC的周长为18,则△DEF的周长为
(
)
A.54
B.6
C.3
D.2
7.如图,圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影(圆形).已知桌面的直径为1.2米,桌面距地面1米.若灯泡距离地面3米,则地面上阴影部分的面积为
(
)
A.0.36π平方米
B.0.81π平方米
C.2π平方米
D.3.24π平方米
8.如图,△ABC的面积是12,D,E,F,G分别是BC,AD,BE,CE的中点,则△AFG的面积是
(
)
A.4.5
B.5
C.5.5
D.6
9.如图,在一块斜边长30
cm的直角三角形木板(Rt△ACB)上截取一个正方形CDEF,点D在边BC上,点E在斜边AB上,点F在边AC上.若AF∶AC=1∶3,则这块木板截取正方形CDEF后,剩余部分的面积为
(
)
A.100
cm2
B.150
cm2
C.170
cm2
D.200
cm2
10.如图,在矩形ABCD中,E是CD边的中点,且BE⊥AC于点F,连接DF,则下列结论错误的是(
)
A.△ADC∽△CFB
B.AD=DF
C.
D.
二、填空题
11.已知△ABC∽△DEF,其中AB=6,BC=8,AC=12,DE=3,那么△DEF的周长为
.?
12.如图,在△ABC中,点D,E分别在AB,AC上,∠AED=∠B.若AE=2,△ADE的面积为4,四边形BCED的面积为5,则AB的长为
.?
13.如果两个相似三角形对应角平分线的比是4∶9,那么它们的周长比是
.?
14.已知△ABC∽△A'B'C',它们的相似比为7∶9,若△ABC的周长为56
cm,那么△A'B'C'的周长为
.?
15.如果两个相似三角形的相似比是2∶3,较小三角形的面积为4
cm2,那么较大三角形的面积为
cm2.?
16.如图,在△ABD中,∠ACB=90°,直线EF∥BD,交AB于点E,交AC于点G,交AD于点F.若S△AEG=S四边形EBCG,则=?
.?
17.如图,M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1,△2,△3(图中阴影部分)的面积分别是4,9和49,则△ABC的面积是
.?
三、解答题
18.如图,在△ABC中,DE∥BC,且S△ADE∶S四边形BCED=1∶2,BC=2,求DE的长.
19.如图,在平行四边形ABCD中,AE∶EB=1∶2.
(1)求△AEF与△CDF的周长之比;
(2)若=6
,求.
20.如图,已知AC∥BD,AB和CD相交于点E,AC=6,BD=4,F是BC上一点,且S△BEF∶S△EFC=2∶3.
(1)求EF的长;
(2)如果△BEF的面积为4,求△ABC的面积.
21.已知△ABC∽△A'B'C',,AB边上的中线CD=4
cm,△ABC的周长为20
cm,△A'B'C'的面积为64
cm2.
(1)求A'B'边上的中线C'D'的长;
(2)求△A'B'C'的周长;
(3)求△ABC的面积.
22.如图,D,E分别是△ABC的边BC,AB上的点,△ABC,△BDE,△ACD的周长依次为m,m1,m2.
(1)当∠2=∠3,BD=BC时,求的值;
(2)当∠1=∠2,BD=BC时,求的值.
参考答案
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
答案
A
B
C
C
C
B
B
A
A
C
二、填空题
11. 13
12. 3
13. 4∶9
14. 72
cm
15. 9
16.?
17. 144
【提示】如图,易得△DEM∽△MPQ∽△FMG∽△ABC,∴EM∶MG∶PQ=2∶3∶7,∴EM∶BC=2∶12=1∶6,∴S△ABC=36×4=144.
三、解答题
18.解:DE=2.
19.解:(1)因为四边形ABCD是平行四边形,
所以AB=CD,AB∥CD,所以△AEF∽△CDF.
因为AE∶EB=1∶2,所以AE∶AB=AE∶CD=1∶3,
所以△AEF与△CDF的周长之比为1∶3.
(2)由(1)知,△AEF∽△CDF,相似比为1∶3,
所以它们的面积之比为1∶9.
因为=6
,所以=54
.
20.解:(1)∵AC∥BD,∴.
∵△BEF和△EFC同高,且S△BEF∶S△EFC=2∶3,
∴,∴,即,
∴△BEF∽△BAC,∴,
∴EF=×6=.
(2)∵△BEF∽△BAC,∴,
∴S△ABC=25.
21.解:(1)∵△ABC∽△A'B'C',,AB边上的中线CD=4
cm,∴,∴C'D'=4×2=8(cm),
即A'B'边上的中线C'D'的长为8
cm.
(2)∵△ABC∽△A'B'C',,△ABC的周长为20
cm,
∴,∴C△A'B'C'=20×2=40(cm),
∴△A'B'C'的周长为40
cm.
(3)∵△ABC∽△A'B'C',,△A'B'C'的面积为64
cm2,∴,
∴S△ABC=64÷4=16(cm2),即△ABC的面积为16
cm2.
22.解:(1)∵∠2=∠3,∴DE∥AC,
∴△BDE∽△BCA,∴,
由BD=BC,得,即.
(2)∵∠1=∠2,∠C是公共角,
∴△ACD∽△BCA,∴,
∴.
由BD=BC,得DC=BC,
∴.
