沪科版九年级上册数学同步练习 23.1 第1课时 正切(Word版 含答案)
文档属性
| 名称 | 沪科版九年级上册数学同步练习 23.1 第1课时 正切(Word版 含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 200.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-25 00:00:00 | ||
图片预览


文档简介
沪科版九年级上册数学同步练习
第23章 解直角三角形
23.1 锐角的三角函数
第1课时 正 切
一、选择题
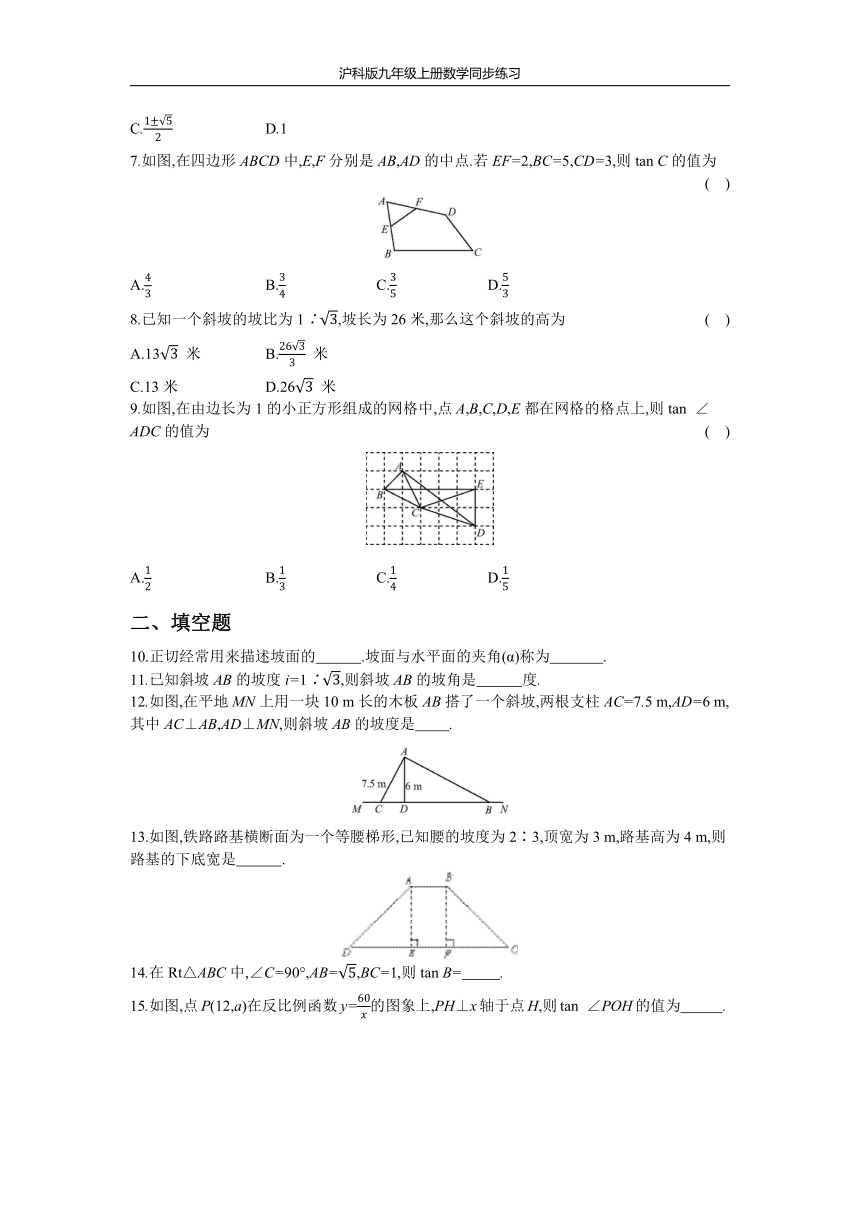
1.如图,锐角α的顶点在原点,始边在x轴的正半轴上,终边上一点P的坐标为(2,3),那么tan
α的值等于
(
)
A.
B.
C.
D.
2.如图,在Rt△ABC中,∠C为直角,CD⊥AB于点D.已知AC=3,AB=5,则tan
∠BCD等于(
)
A.
B.
C.
D.
3.在Rt△ABC中,∠A=90°,AB=12,AC=5,那么tan
B等于
(
)
A.
B.
C.
D.
4.在Rt△ABC中,∠C=90°,AB=5,tan
B=,则AC的长为
(
)
A.3
B.4
C.
D.2
5.如图所示,河堤横断面迎水坡AB的坡比是1∶,堤高BC=4
m,则坡面AB的长度是
(
)
A.
m
B.4
m
C.2
m
D.4
m
6.在△ABC中,∠C=90°,a,b分别是∠A,∠B的对边,a2-ab-b2=0,则tan
A=
(
)
A.
B.
C.
D.1
7.如图,在四边形ABCD中,E,F分别是AB,AD的中点.若EF=2,BC=5,CD=3,则tan
C的值为
(
)
A.
B.
C.
D.
8.已知一个斜坡的坡比为1∶,坡长为26米,那么这个斜坡的高为
(
)
A.13
米
B.
米
C.13米
D.26
米
9.如图,在由边长为1的小正方形组成的网格中,点A,B,C,D,E都在网格的格点上,则tan
∠ADC的值为
(
)
A.
B.
C.
D.
二、填空题
10.正切经常用来描述坡面的
.坡面与水平面的夹角(α)称为
.?
11.已知斜坡AB的坡度i=1∶,则斜坡AB的坡角是
度.?
12.如图,在平地MN上用一块10
m长的木板AB搭了一个斜坡,两根支柱AC=7.5
m,AD=6
m,其中AC⊥AB,AD⊥MN,则斜坡AB的坡度是?
.?
13.如图,铁路路基横断面为一个等腰梯形,已知腰的坡度为2∶3,顶宽为3
m,路基高为4
m,则路基的下底宽是
.?
14.在Rt△ABC中,∠C=90°,AB=,BC=1,则tan
B=
.?
15.如图,点P(12,a)在反比例函数y=的图象上,PH⊥x轴于点H,则tan
∠POH的值为?
.?
16.如图,已知两点A(2,0),B(0,4),且∠1=∠2,则tan
∠OCA的值为
.?
三、解答题
17.在△ABC中,AB=AC=10,BC=16,求tan
B的值.
18.在Rt△ABC中,∠C=90°,AC=12,tan
A=,求AB的长.
19.如图,将矩形ABCD沿CE折叠,点B恰好落在边AD上的点F处.如果,求tan∠DCF的值.
20.如图,修建的二滩水库大坝的横断面是梯形,坝顶宽6
m,坝高23
m,斜坡AB的坡度i=1∶3,斜坡CD的坡度i=1∶2.5.求坝底宽AD.
21.如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,∠A=30°,AD=20.求BC的长.
22.如图,把n个边长为1的正方形拼接成一排.
(1)易得tan
∠BA1C=1,求tan
∠BA4C的值;(写出求解过程)
(2)按此规律,写出tan
∠BAnC=? .(用含n的代数式表示)?
参考答案
一、选择题
题号
1
2
3
4
5
6
7
8
9
答案
B
B
B
B
D
A
A
C
B
9.【提示】根据题意可得,AC=BC=,CD=CE=,AD=BE=5,∴△ACD≌△BCE,∴∠ADC=∠BEC,∴tan
∠ADC=tan
∠BEC=.
二、填空题
10. 坡度 坡角
11. 30
12.?
13. 15
m
14. 2
15.?
16. 2
三、解答题
17.解:如图,在△ABC中,AB=AC=10,BC=16,
过点A作AD⊥BC于点D,则BD=8.
在Rt△ABD中,
AD===6,
故tan
B===.
18.解:AB=15.
19.解:∵四边形ABCD是矩形,
∴AB=CD,∠D=90°.
由题可知CF=BC.
∵,∴.
设CD=2x(x>0),CF=3x,
∴DF=x,
∴tan
∠DCF=.
20.解:∵AB的坡度i=1∶3,BE=23
m,
∴AE=69
m.
∵CD的坡度i=1∶2.5,CF=23
m,
∴DF=57.5
m.
又∵EF=BC=6
m,
∴AD=AE+EF+DF=132.5
m.
21.解:∵∠C=90°,∠A=30°,∴∠ABC=60°.
又∵BD平分∠ABC,
∴∠A=∠ABD=∠CBD=30°,
∴AD=BD=20,∴CD=10,
∴AC=AD+CD=30.
∵tan
A=,∴BC=AC·tan
A=30×=10.
22.解:(1)过点C作CE⊥A4B于点E,易得∠A4BC=∠BA4A1,
故tan
∠A4BC=tan
∠BA4A1=.
在Rt△BCE中,由tan
∠A4BC=,得BE=4CE,又BC=1,所以BE=,CE=,而A4B=,
所以A4E=A4B-BE=,
在Rt△A4EC中,tan
∠BA4C=.
(2)提示:根据前面的规律,不难得出tan
∠BA1C=,tan
∠BA2C=,
tan
∠BA3C=,tan
∠BA4C=,
则可得规律tan
∠BAnC=.
第23章 解直角三角形
23.1 锐角的三角函数
第1课时 正 切
一、选择题
1.如图,锐角α的顶点在原点,始边在x轴的正半轴上,终边上一点P的坐标为(2,3),那么tan
α的值等于
(
)
A.
B.
C.
D.
2.如图,在Rt△ABC中,∠C为直角,CD⊥AB于点D.已知AC=3,AB=5,则tan
∠BCD等于(
)
A.
B.
C.
D.
3.在Rt△ABC中,∠A=90°,AB=12,AC=5,那么tan
B等于
(
)
A.
B.
C.
D.
4.在Rt△ABC中,∠C=90°,AB=5,tan
B=,则AC的长为
(
)
A.3
B.4
C.
D.2
5.如图所示,河堤横断面迎水坡AB的坡比是1∶,堤高BC=4
m,则坡面AB的长度是
(
)
A.
m
B.4
m
C.2
m
D.4
m
6.在△ABC中,∠C=90°,a,b分别是∠A,∠B的对边,a2-ab-b2=0,则tan
A=
(
)
A.
B.
C.
D.1
7.如图,在四边形ABCD中,E,F分别是AB,AD的中点.若EF=2,BC=5,CD=3,则tan
C的值为
(
)
A.
B.
C.
D.
8.已知一个斜坡的坡比为1∶,坡长为26米,那么这个斜坡的高为
(
)
A.13
米
B.
米
C.13米
D.26
米
9.如图,在由边长为1的小正方形组成的网格中,点A,B,C,D,E都在网格的格点上,则tan
∠ADC的值为
(
)
A.
B.
C.
D.
二、填空题
10.正切经常用来描述坡面的
.坡面与水平面的夹角(α)称为
.?
11.已知斜坡AB的坡度i=1∶,则斜坡AB的坡角是
度.?
12.如图,在平地MN上用一块10
m长的木板AB搭了一个斜坡,两根支柱AC=7.5
m,AD=6
m,其中AC⊥AB,AD⊥MN,则斜坡AB的坡度是?
.?
13.如图,铁路路基横断面为一个等腰梯形,已知腰的坡度为2∶3,顶宽为3
m,路基高为4
m,则路基的下底宽是
.?
14.在Rt△ABC中,∠C=90°,AB=,BC=1,则tan
B=
.?
15.如图,点P(12,a)在反比例函数y=的图象上,PH⊥x轴于点H,则tan
∠POH的值为?
.?
16.如图,已知两点A(2,0),B(0,4),且∠1=∠2,则tan
∠OCA的值为
.?
三、解答题
17.在△ABC中,AB=AC=10,BC=16,求tan
B的值.
18.在Rt△ABC中,∠C=90°,AC=12,tan
A=,求AB的长.
19.如图,将矩形ABCD沿CE折叠,点B恰好落在边AD上的点F处.如果,求tan∠DCF的值.
20.如图,修建的二滩水库大坝的横断面是梯形,坝顶宽6
m,坝高23
m,斜坡AB的坡度i=1∶3,斜坡CD的坡度i=1∶2.5.求坝底宽AD.
21.如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,∠A=30°,AD=20.求BC的长.
22.如图,把n个边长为1的正方形拼接成一排.
(1)易得tan
∠BA1C=1,求tan
∠BA4C的值;(写出求解过程)
(2)按此规律,写出tan
∠BAnC=? .(用含n的代数式表示)?
参考答案
一、选择题
题号
1
2
3
4
5
6
7
8
9
答案
B
B
B
B
D
A
A
C
B
9.【提示】根据题意可得,AC=BC=,CD=CE=,AD=BE=5,∴△ACD≌△BCE,∴∠ADC=∠BEC,∴tan
∠ADC=tan
∠BEC=.
二、填空题
10. 坡度 坡角
11. 30
12.?
13. 15
m
14. 2
15.?
16. 2
三、解答题
17.解:如图,在△ABC中,AB=AC=10,BC=16,
过点A作AD⊥BC于点D,则BD=8.
在Rt△ABD中,
AD===6,
故tan
B===.
18.解:AB=15.
19.解:∵四边形ABCD是矩形,
∴AB=CD,∠D=90°.
由题可知CF=BC.
∵,∴.
设CD=2x(x>0),CF=3x,
∴DF=x,
∴tan
∠DCF=.
20.解:∵AB的坡度i=1∶3,BE=23
m,
∴AE=69
m.
∵CD的坡度i=1∶2.5,CF=23
m,
∴DF=57.5
m.
又∵EF=BC=6
m,
∴AD=AE+EF+DF=132.5
m.
21.解:∵∠C=90°,∠A=30°,∴∠ABC=60°.
又∵BD平分∠ABC,
∴∠A=∠ABD=∠CBD=30°,
∴AD=BD=20,∴CD=10,
∴AC=AD+CD=30.
∵tan
A=,∴BC=AC·tan
A=30×=10.
22.解:(1)过点C作CE⊥A4B于点E,易得∠A4BC=∠BA4A1,
故tan
∠A4BC=tan
∠BA4A1=.
在Rt△BCE中,由tan
∠A4BC=,得BE=4CE,又BC=1,所以BE=,CE=,而A4B=,
所以A4E=A4B-BE=,
在Rt△A4EC中,tan
∠BA4C=.
(2)提示:根据前面的规律,不难得出tan
∠BA1C=,tan
∠BA2C=,
tan
∠BA3C=,tan
∠BA4C=,
则可得规律tan
∠BAnC=.
