沪科版九年级上册数学同步练习 23.2 第2课时 仰角、俯角与方位角(Word版 含答案)
文档属性
| 名称 | 沪科版九年级上册数学同步练习 23.2 第2课时 仰角、俯角与方位角(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 246.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-25 10:31:32 | ||
图片预览

文档简介
沪科版九年级上册数学同步练习
第2课时 仰角、俯角与方位角
一、选择题
1.某飞机于空中A处探测到地面目标B,此时从飞机上看目标B的俯角α=30°,飞行高度AC=1200米,则飞机到目标B的距离AB为
(
)
A.1200米
B.2400米
C.400
米
D.1200
米
2.如图,小丹家(图中O点)门前有一条东西走向的公路,经测得有一座水塔(图中A点)在她家北偏东60°的方向上距离500
m处,那么水塔所在的位置到公路的距离AB是
(
)
A.250
m
B.250
m
C.
m
D.250
m
3.如图,小亮为了测量校园里教学楼AB的高度,将测角仪CD竖直放置在与教学楼水平距离为18
m的地面上.若测角仪的高度为1.5
m,测得教学楼的顶部A处的仰角为30°,则教学楼的高度是
(
)
A.55.5
m
B.54
m
C.19.5
m
D.18
m
4.如图是直立在京台高速合肥段的公路边的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为
(
)
A.4
米
B.(2+2)米
C.(4-4)米
D.(4-4)米
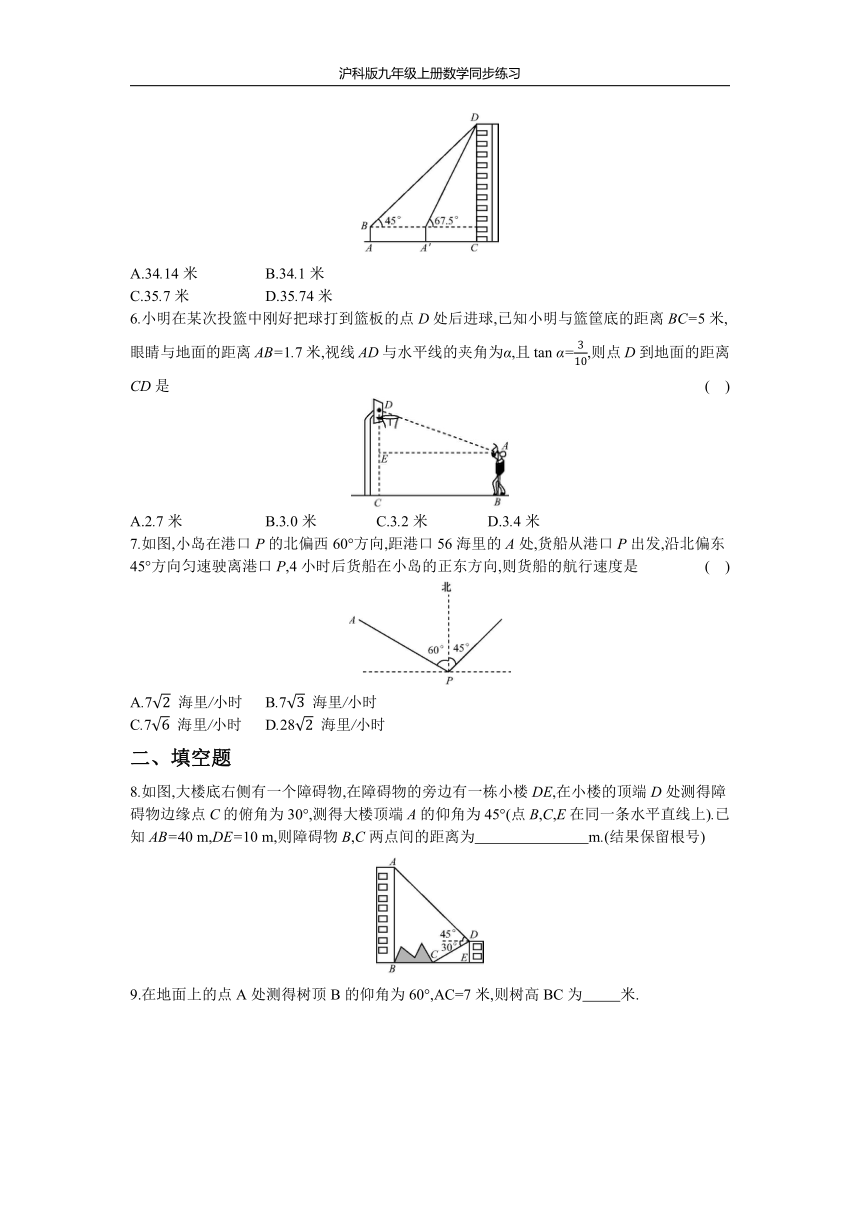
5.如图,数学实践活动小组要测量学校附近楼房CD的高度,在水平地面A处安置测倾器测得楼房CD顶部点D的仰角为45°,向前走20米到达A'处,测得点D的仰角为67.5°.已知测倾器AB的高度为1.6米,则楼房CD的高度约为(结果精确到0.1米,≈1.414,tan
67.5°≈2.414)
(
)
A.34.14米
B.34.1米
C.35.7米
D.35.74米
6.小明在某次投篮中刚好把球打到篮板的点D处后进球,已知小明与篮筐底的距离BC=5米,眼睛与地面的距离AB=1.7米,视线AD与水平线的夹角为α,且tan
α=,则点D到地面的距离CD是
(
)
A.2.7米
B.3.0米
C.3.2米
D.3.4米
7.如图,小岛在港口P的北偏西60°方向,距港口56海里的A处,货船从港口P出发,沿北偏东45°方向匀速驶离港口P,4小时后货船在小岛的正东方向,则货船的航行速度是
(
)
A.7
海里/小时
B.7
海里/小时
C.7
海里/小时
D.28
海里/小时
二、填空题
8.如图,大楼底右侧有一个障碍物,在障碍物的旁边有一栋小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一条水平直线上).已知AB=40
m,DE=10
m,则障碍物B,C两点间的距离为
m.(结果保留根号)?
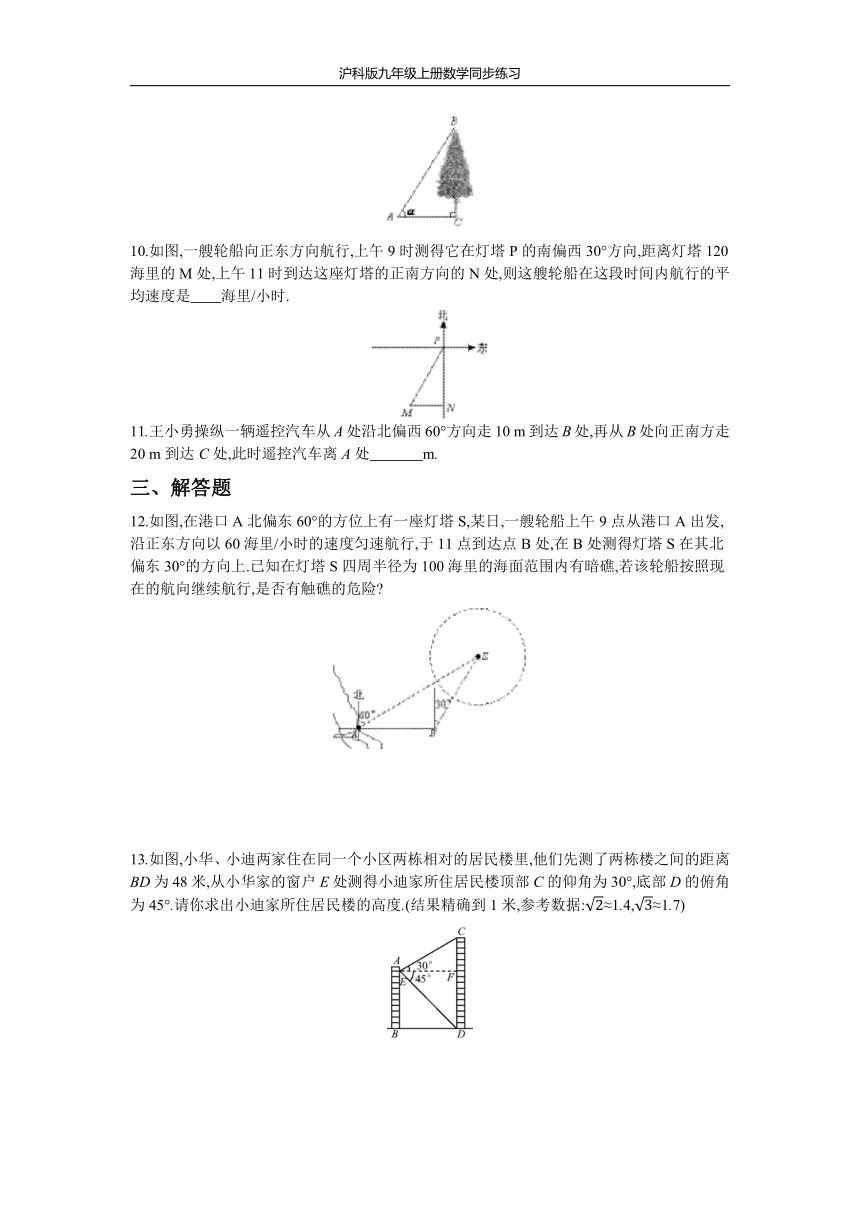
9.在地面上的点A处测得树顶B的仰角为60°,AC=7米,则树高BC为
米.?
10.如图,一艘轮船向正东方向航行,上午9时测得它在灯塔P的南偏西30°方向,距离灯塔120海里的M处,上午11时到达这座灯塔的正南方向的N处,则这艘轮船在这段时间内航行的平均速度是 海里/小时.?
11.王小勇操纵一辆遥控汽车从A处沿北偏西60°方向走10
m到达B处,再从B处向正南方走20
m到达C处,此时遥控汽车离A处
m.?
三、解答题
12.如图,在港口A北偏东60°的方位上有一座灯塔S,某日,一艘轮船上午9点从港口A出发,沿正东方向以60海里/小时的速度匀速航行,于11点到达点B处,在B处测得灯塔S在其北偏东30°的方向上.已知在灯塔S四周半径为100海里的海面范围内有暗礁,若该轮船按照现在的航向继续航行,是否有触礁的危险?
13.如图,小华、小迪两家住在同一个小区两栋相对的居民楼里,他们先测了两栋楼之间的距离BD为48米,从小华家的窗户E处测得小迪家所住居民楼顶部C的仰角为30°,底部D的俯角为45°.请你求出小迪家所住居民楼的高度.(结果精确到1米,参考数据:≈1.4,≈1.7)
14.一艘轮船位于灯塔P南偏西60°方向,距离灯塔20海里的A处,则它向东航行多少海里到达灯塔P南偏西45°方向上的B处?(结果精确到0.1海里,参考数据:≈1.732)
15.如图,从热气球C上测得两建筑物A,B底部的俯角分别为30°和60°.如果这时热气球的高度CD为90米,且点A,D,B在同一条直线上,求建筑物A,B间的距离.
16.如图,一艘轮船在A处测得灯塔P在船的北偏东30°的方向,轮船沿着北偏东60°的方向航行16
km后到达B处,这时灯塔P在船的北偏西75°的方向.求灯塔P与B之间的距离.(结果保留根号)
17.下图为某区域部分交通线路图,其中直线l1∥l2∥l3,直线l与直线l1,l2,l3都垂直,垂足分别为点A、点B和点C(高速路右侧边缘),l2上的点M位于点A的北偏东30°方向上,且BM=
千米,l3上的点N位于点M的北偏东α方向上,且cos
α=,MN=2
千米,点A和点N是城际线L上的两个相邻的站点.
(1)求l2和l3之间的距离;
(2)若城际火车的平均速度为150千米/小时,求市民小强乘坐城际火车从站点A到站点N需要多少小时?(结果用分数表示)
参考答案
一、选择题
题号
1
2
3
4
5
6
7
答案
B
A
C
D
C
C
A
二、填空题
8. 30-10
9. 7
10. 30
11. 10
三、解答题
12.解:过点S作SC⊥AB于点C.
由题意,得∠SAB=90°-60°=30°,∠SBC=90°-30°=60°,
∴∠ASB=30°=∠SAB,∴SB=AB=2×60=120(海里).
在Rt△BSC中,∵sin
60°=,∴SC=120×=60≈104>100.
∴该轮船按照现在的航向继续航行,没有触礁的危险.
13.解:在Rt△ECF中,CF=EF·tan
30°=48×=16(米),
∴CD=CF+FD=16+48≈75(米),
答:小迪家所住居民楼的高度约为75米.
14.解:如图,由题得AC⊥PC,∠APC=60°,∠BPC=45°,AP=20海里,
在Rt△APC中,PC=AP·cos
∠APC=10(海里),AC=AP·sin
∠APC=10(海里).
在Rt△PBC中,∵∠BPC=45°,
∴△PBC为等腰直角三角形,
∴BC=PC=10(海里),∴AB=AC-BC≈7.3(海里).
答:轮船向东航行约7.3海里到达灯塔P南偏西45°方向上的B处.
15.解:在Rt△ACD中,AD==90(米).
在Rt△BCD中,BD==30(米),
∴AB=AD+BD=120(米).
答:建筑物A,B间的距离为120米.
16.解:过点P作PH⊥AB于点H.
由题意得∠PAB=30°,∠PBA=45°.
设PH=x,∴AH=x,BH=x,PB=x,
∵AB=16,∴x+x=16,解得x=8-8,
∴PB=x=8-8.
答:灯塔P与B之间的距离为(8-8)km.
17.解:(1)过点M作MD⊥NC于点D.
∵cos
α=,MN=2
千米,
∴cos
α=,解得DM=2.
答:l2和l3之间的距离为2千米.
(2)∵点M位于点A的北偏东30°方向上,且BM=
千米,
∴tan
30°=,解得AB=3,
可得AC=3+2=5.
∵MN=2,DM=2,
∴DN==4,
∴NC=DN+BM=5,
∴AN==10(千米).
∵城际火车的平均速度为150千米/小时,
∴市民小强乘坐城际火车从站点A到站点N需要小时.
第2课时 仰角、俯角与方位角
一、选择题
1.某飞机于空中A处探测到地面目标B,此时从飞机上看目标B的俯角α=30°,飞行高度AC=1200米,则飞机到目标B的距离AB为
(
)
A.1200米
B.2400米
C.400
米
D.1200
米
2.如图,小丹家(图中O点)门前有一条东西走向的公路,经测得有一座水塔(图中A点)在她家北偏东60°的方向上距离500
m处,那么水塔所在的位置到公路的距离AB是
(
)
A.250
m
B.250
m
C.
m
D.250
m
3.如图,小亮为了测量校园里教学楼AB的高度,将测角仪CD竖直放置在与教学楼水平距离为18
m的地面上.若测角仪的高度为1.5
m,测得教学楼的顶部A处的仰角为30°,则教学楼的高度是
(
)
A.55.5
m
B.54
m
C.19.5
m
D.18
m
4.如图是直立在京台高速合肥段的公路边的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为
(
)
A.4
米
B.(2+2)米
C.(4-4)米
D.(4-4)米
5.如图,数学实践活动小组要测量学校附近楼房CD的高度,在水平地面A处安置测倾器测得楼房CD顶部点D的仰角为45°,向前走20米到达A'处,测得点D的仰角为67.5°.已知测倾器AB的高度为1.6米,则楼房CD的高度约为(结果精确到0.1米,≈1.414,tan
67.5°≈2.414)
(
)
A.34.14米
B.34.1米
C.35.7米
D.35.74米
6.小明在某次投篮中刚好把球打到篮板的点D处后进球,已知小明与篮筐底的距离BC=5米,眼睛与地面的距离AB=1.7米,视线AD与水平线的夹角为α,且tan
α=,则点D到地面的距离CD是
(
)
A.2.7米
B.3.0米
C.3.2米
D.3.4米
7.如图,小岛在港口P的北偏西60°方向,距港口56海里的A处,货船从港口P出发,沿北偏东45°方向匀速驶离港口P,4小时后货船在小岛的正东方向,则货船的航行速度是
(
)
A.7
海里/小时
B.7
海里/小时
C.7
海里/小时
D.28
海里/小时
二、填空题
8.如图,大楼底右侧有一个障碍物,在障碍物的旁边有一栋小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一条水平直线上).已知AB=40
m,DE=10
m,则障碍物B,C两点间的距离为
m.(结果保留根号)?
9.在地面上的点A处测得树顶B的仰角为60°,AC=7米,则树高BC为
米.?
10.如图,一艘轮船向正东方向航行,上午9时测得它在灯塔P的南偏西30°方向,距离灯塔120海里的M处,上午11时到达这座灯塔的正南方向的N处,则这艘轮船在这段时间内航行的平均速度是 海里/小时.?
11.王小勇操纵一辆遥控汽车从A处沿北偏西60°方向走10
m到达B处,再从B处向正南方走20
m到达C处,此时遥控汽车离A处
m.?
三、解答题
12.如图,在港口A北偏东60°的方位上有一座灯塔S,某日,一艘轮船上午9点从港口A出发,沿正东方向以60海里/小时的速度匀速航行,于11点到达点B处,在B处测得灯塔S在其北偏东30°的方向上.已知在灯塔S四周半径为100海里的海面范围内有暗礁,若该轮船按照现在的航向继续航行,是否有触礁的危险?
13.如图,小华、小迪两家住在同一个小区两栋相对的居民楼里,他们先测了两栋楼之间的距离BD为48米,从小华家的窗户E处测得小迪家所住居民楼顶部C的仰角为30°,底部D的俯角为45°.请你求出小迪家所住居民楼的高度.(结果精确到1米,参考数据:≈1.4,≈1.7)
14.一艘轮船位于灯塔P南偏西60°方向,距离灯塔20海里的A处,则它向东航行多少海里到达灯塔P南偏西45°方向上的B处?(结果精确到0.1海里,参考数据:≈1.732)
15.如图,从热气球C上测得两建筑物A,B底部的俯角分别为30°和60°.如果这时热气球的高度CD为90米,且点A,D,B在同一条直线上,求建筑物A,B间的距离.
16.如图,一艘轮船在A处测得灯塔P在船的北偏东30°的方向,轮船沿着北偏东60°的方向航行16
km后到达B处,这时灯塔P在船的北偏西75°的方向.求灯塔P与B之间的距离.(结果保留根号)
17.下图为某区域部分交通线路图,其中直线l1∥l2∥l3,直线l与直线l1,l2,l3都垂直,垂足分别为点A、点B和点C(高速路右侧边缘),l2上的点M位于点A的北偏东30°方向上,且BM=
千米,l3上的点N位于点M的北偏东α方向上,且cos
α=,MN=2
千米,点A和点N是城际线L上的两个相邻的站点.
(1)求l2和l3之间的距离;
(2)若城际火车的平均速度为150千米/小时,求市民小强乘坐城际火车从站点A到站点N需要多少小时?(结果用分数表示)
参考答案
一、选择题
题号
1
2
3
4
5
6
7
答案
B
A
C
D
C
C
A
二、填空题
8. 30-10
9. 7
10. 30
11. 10
三、解答题
12.解:过点S作SC⊥AB于点C.
由题意,得∠SAB=90°-60°=30°,∠SBC=90°-30°=60°,
∴∠ASB=30°=∠SAB,∴SB=AB=2×60=120(海里).
在Rt△BSC中,∵sin
60°=,∴SC=120×=60≈104>100.
∴该轮船按照现在的航向继续航行,没有触礁的危险.
13.解:在Rt△ECF中,CF=EF·tan
30°=48×=16(米),
∴CD=CF+FD=16+48≈75(米),
答:小迪家所住居民楼的高度约为75米.
14.解:如图,由题得AC⊥PC,∠APC=60°,∠BPC=45°,AP=20海里,
在Rt△APC中,PC=AP·cos
∠APC=10(海里),AC=AP·sin
∠APC=10(海里).
在Rt△PBC中,∵∠BPC=45°,
∴△PBC为等腰直角三角形,
∴BC=PC=10(海里),∴AB=AC-BC≈7.3(海里).
答:轮船向东航行约7.3海里到达灯塔P南偏西45°方向上的B处.
15.解:在Rt△ACD中,AD==90(米).
在Rt△BCD中,BD==30(米),
∴AB=AD+BD=120(米).
答:建筑物A,B间的距离为120米.
16.解:过点P作PH⊥AB于点H.
由题意得∠PAB=30°,∠PBA=45°.
设PH=x,∴AH=x,BH=x,PB=x,
∵AB=16,∴x+x=16,解得x=8-8,
∴PB=x=8-8.
答:灯塔P与B之间的距离为(8-8)km.
17.解:(1)过点M作MD⊥NC于点D.
∵cos
α=,MN=2
千米,
∴cos
α=,解得DM=2.
答:l2和l3之间的距离为2千米.
(2)∵点M位于点A的北偏东30°方向上,且BM=
千米,
∴tan
30°=,解得AB=3,
可得AC=3+2=5.
∵MN=2,DM=2,
∴DN==4,
∴NC=DN+BM=5,
∴AN==10(千米).
∵城际火车的平均速度为150千米/小时,
∴市民小强乘坐城际火车从站点A到站点N需要小时.
