沪科版九年级上册数学同步练习 23.2 第3课时 解直角三角形的应用(Word版 含答案)
文档属性
| 名称 | 沪科版九年级上册数学同步练习 23.2 第3课时 解直角三角形的应用(Word版 含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 280.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-25 00:00:00 | ||
图片预览


文档简介
沪科版九年级上册数学同步练习
第3课时 解直角三角形的应用
一、选择题
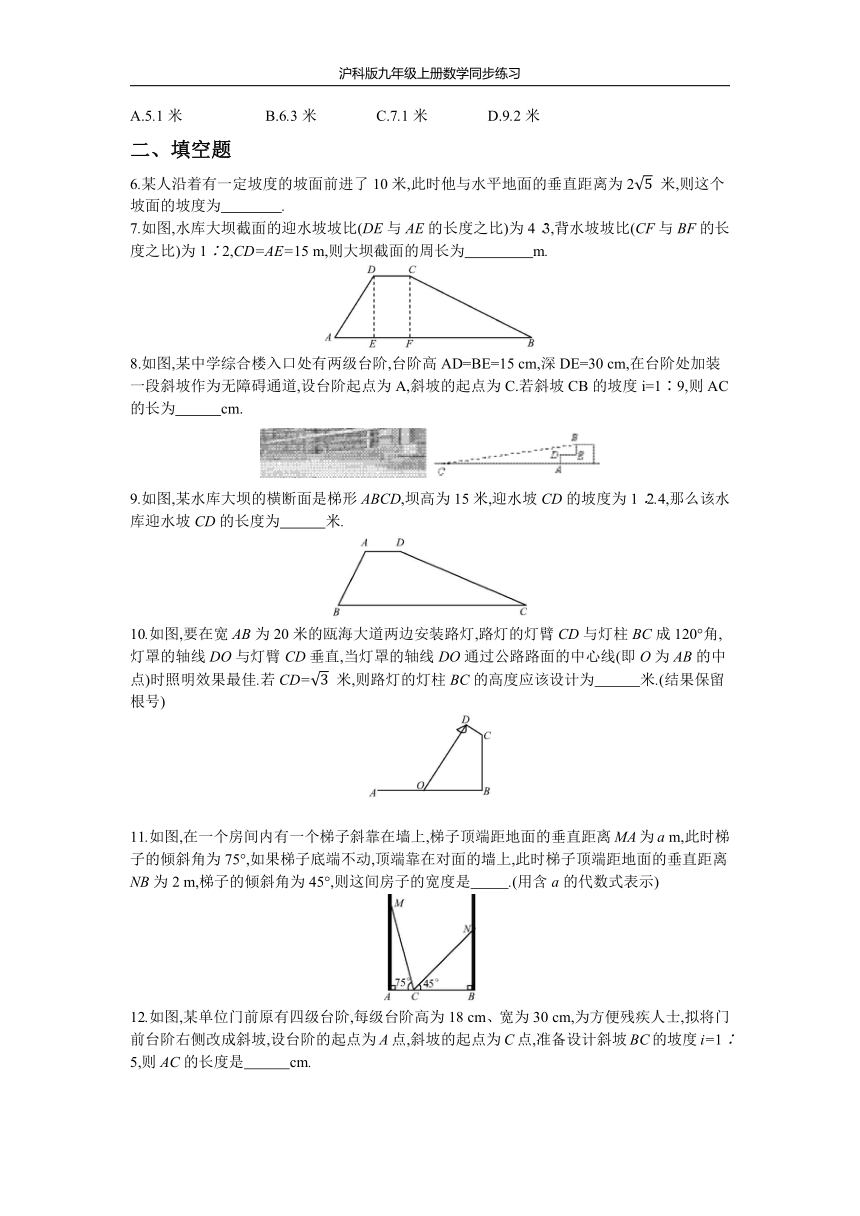
1.如图,河堤横断面迎水坡AB的坡比是1∶,堤高BC=4
m,则迎水坡宽度AC的长为
(
)
A.
m
B.4
m
C.2
m
D.4
m
2.如图,传送带和地面所成斜坡AB的坡度为1∶2,物体从地面沿着该斜坡前进了10米,那么物体离地面的高度为
(
)
A.5
米
B.5
米
C.2
米
D.4
米
3.如图,城关镇某村准备在坡角为α的山坡上栽树,要求相邻两棵树之间的水平距离为m米,那么两棵树在坡面上的距离AB为
(
)
A.mcos
α
B.
C.msin
α
D.
4.如图,某商店营业大厅自动扶梯AB的坡比为1∶(坡比是坡面的铅直高度BC与水平宽度AC之比),已知AB的长为12米,则大厅两层之间的高度BC为
(
)
A.6米
B.6
米
C.4
米
D.4米
5.如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1∶0.75,坡长BC=10米,则此时AB的长约为(参考数据:sin
40°≈0.64,cos
40°≈0.77,tan
40°≈0.84)
(
)
A.5.1米
B.6.3米
C.7.1米
D.9.2米
二、填空题
6.某人沿着有一定坡度的坡面前进了10米,此时他与水平地面的垂直距离为2
米,则这个坡面的坡度为
.?
7.如图,水库大坝截面的迎水坡坡比(DE与AE的长度之比)为4∶3,背水坡坡比(CF与BF的长度之比)为1∶2,CD=AE=15
m,则大坝截面的周长为
m.?
8.如图,某中学综合楼入口处有两级台阶,台阶高AD=BE=15
cm,深DE=30
cm,在台阶处加装一段斜坡作为无障碍通道,设台阶起点为A,斜坡的起点为C.若斜坡CB的坡度i=1∶9,则AC的长为
cm.?
9.如图,某水库大坝的横断面是梯形ABCD,坝高为15米,迎水坡CD的坡度为1∶2.4,那么该水库迎水坡CD的长度为
米.?
10.如图,要在宽AB为20米的瓯海大道两边安装路灯,路灯的灯臂CD与灯柱BC成120°角,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线(即O为AB的中点)时照明效果最佳.若CD=
米,则路灯的灯柱BC的高度应该设计为
米.(结果保留根号)?
11.如图,在一个房间内有一个梯子斜靠在墙上,梯子顶端距地面的垂直距离MA为a
m,此时梯子的倾斜角为75°,如果梯子底端不动,顶端靠在对面的墙上,此时梯子顶端距地面的垂直距离NB为2
m,梯子的倾斜角为45°,则这间房子的宽度是
.(用含a的代数式表示)?
12.如图,某单位门前原有四级台阶,每级台阶高为18
cm、宽为30
cm,为方便残疾人士,拟将门前台阶右侧改成斜坡,设台阶的起点为A点,斜坡的起点为C点,准备设计斜坡BC的坡度i=1∶5,则AC的长度是
cm.?
13.有一种落地晾衣架如图1所示,其原理是通过改变两根支撑杆夹角的度数来调整晾衣杆的高度.图2是支撑杆的平面示意图,AB和CD分别是两根不同长度的支撑杆,夹角∠BOD=α.若AO=85
cm,BO=DO=65
cm.问:当α=74°时,较长支撑杆的端点A离地面的高度h约为
cm.(参考数据:
sin
37°≈0.6,cos
37°≈0.8,sin
53°≈0.8,cos
53°≈0.6)?
三、解答题
14.如图,某幼儿园为了加强安全管理,决定将园内滑梯的倾斜角由45°降为30°,已知点D,B,C在同一水平地面上,且BD的长为2(-1)米,求改造后滑梯的长度.
15.如图,有一段斜坡BC的长为10米,坡角∠CBD=12°,为方便残疾人的轮椅车通行,现准备把坡角降为5°.
(1)求坡高CD;
(2)求斜坡新起点A与原起点B的距离.
(结果精确到0.1米,参考数据:sin
12°≈0.21,cos
12°≈0.98,tan
5°≈0.09)
16.某小区为了安全起见,决定将小区内的滑滑板的倾斜角由45°调为30°.如图,已知原滑滑板AB的长为4米,点D,B,C在同一水平地面上,调整后滑滑板会加长多少米?(结果精确到0.01米,参考数据:≈1.414,≈1.732,≈2.449)
17.如图,防洪大堤的横断面是梯形ABCD,其中AD∥BC,坡角α=60°,汛期来临前对其进行了加固,改造后的背水面坡角β=45°.若原坡长AB=20
m,求改造后的坡长AE.(结果保留根号)
18.如图1,水坝的横截面是梯形ABCD,∠ABC=37°,坝顶DC=3
m,背水坡AD的坡度i(即tan
∠DAB)为1∶0.5,坝底AB=14
m.
(1)求坝高;
(2)如图2,为了提高堤坝的防洪抗洪能力,防汛指挥部决定在背水坡将坝顶和坝底同时拓宽加固,使得AE=2DF,EF⊥BF,求DF的长.(参考数据:sin
37°≈,cos
37°≈,tan
37°≈)
参考答案
一、选择题
题号
1
2
3
4
5
答案
B
C
B
A
A
二、填空题
6. 1∶2
7. 110+20
8. 240
9. 39
10. 8 米
11. a ?
【提示】过点N作ND⊥MA,连接MN,易得△CMN为等边三角形,△ACM≌△DMN,∴DN=AM=a.
12. 270
13. 120
三、解答题
14.解:设AC=x,∴BC=AC=x,
∴tan
30°==,解得x=2,
∴AD=2AC=4.
答:改造后滑梯的长度为4米.
15.解:(1)在Rt△BCD中,CD=BC·sin
12°≈10×0.21=2.1(米).
(2)在Rt△BCD中,BD=BC·cos
12°≈10×0.98=9.8(米),
在Rt△ACD中,AD=≈23.33(米),
AB=AD-BD≈23.33-9.8=13.53≈13.5(米).
16.解:在Rt△ABC中,AC=AB·sin
45°=4×=2,在Rt△ADC中,AD=2AC=4,AD-AB=4-4≈1.66.
答:调整后滑滑板会加长约1.66米.
17.解:过点A作AF⊥BC于点F.
由题知,在Rt△ABF中,α=60°,
∴AF=AB·sin
60°=20×=10
(m).
在Rt△AEF中,β=45°,∴AE==10
(m).
答:改造后的坡长AE为10
m.
18.解:(1)作DM⊥AB于点M,CN⊥AB于点N.
由题意得tan
∠DAB==2.
设AM=x,∴DM=2x.
∵四边形DMNC是矩形,∴DM=CN=2x.
在Rt△NBC中,tan
37°=,
∴BN≈x.
∵x+3+x=14,∴x=3,∴DM=6.
答:坝高为6
m.
(2)作FH⊥AB于点H.设DF=y,∴AE=2y,EH=3+2y-y=3+y,BH=14+2y-(3+y)=11+y,
由△EFH∽△FBH,可得,
即,解得y=-7+2或-7-2(舍),
∴DF=2-7.
答:DF的长为(2-7)m.
第3课时 解直角三角形的应用
一、选择题
1.如图,河堤横断面迎水坡AB的坡比是1∶,堤高BC=4
m,则迎水坡宽度AC的长为
(
)
A.
m
B.4
m
C.2
m
D.4
m
2.如图,传送带和地面所成斜坡AB的坡度为1∶2,物体从地面沿着该斜坡前进了10米,那么物体离地面的高度为
(
)
A.5
米
B.5
米
C.2
米
D.4
米
3.如图,城关镇某村准备在坡角为α的山坡上栽树,要求相邻两棵树之间的水平距离为m米,那么两棵树在坡面上的距离AB为
(
)
A.mcos
α
B.
C.msin
α
D.
4.如图,某商店营业大厅自动扶梯AB的坡比为1∶(坡比是坡面的铅直高度BC与水平宽度AC之比),已知AB的长为12米,则大厅两层之间的高度BC为
(
)
A.6米
B.6
米
C.4
米
D.4米
5.如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1∶0.75,坡长BC=10米,则此时AB的长约为(参考数据:sin
40°≈0.64,cos
40°≈0.77,tan
40°≈0.84)
(
)
A.5.1米
B.6.3米
C.7.1米
D.9.2米
二、填空题
6.某人沿着有一定坡度的坡面前进了10米,此时他与水平地面的垂直距离为2
米,则这个坡面的坡度为
.?
7.如图,水库大坝截面的迎水坡坡比(DE与AE的长度之比)为4∶3,背水坡坡比(CF与BF的长度之比)为1∶2,CD=AE=15
m,则大坝截面的周长为
m.?
8.如图,某中学综合楼入口处有两级台阶,台阶高AD=BE=15
cm,深DE=30
cm,在台阶处加装一段斜坡作为无障碍通道,设台阶起点为A,斜坡的起点为C.若斜坡CB的坡度i=1∶9,则AC的长为
cm.?
9.如图,某水库大坝的横断面是梯形ABCD,坝高为15米,迎水坡CD的坡度为1∶2.4,那么该水库迎水坡CD的长度为
米.?
10.如图,要在宽AB为20米的瓯海大道两边安装路灯,路灯的灯臂CD与灯柱BC成120°角,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线(即O为AB的中点)时照明效果最佳.若CD=
米,则路灯的灯柱BC的高度应该设计为
米.(结果保留根号)?
11.如图,在一个房间内有一个梯子斜靠在墙上,梯子顶端距地面的垂直距离MA为a
m,此时梯子的倾斜角为75°,如果梯子底端不动,顶端靠在对面的墙上,此时梯子顶端距地面的垂直距离NB为2
m,梯子的倾斜角为45°,则这间房子的宽度是
.(用含a的代数式表示)?
12.如图,某单位门前原有四级台阶,每级台阶高为18
cm、宽为30
cm,为方便残疾人士,拟将门前台阶右侧改成斜坡,设台阶的起点为A点,斜坡的起点为C点,准备设计斜坡BC的坡度i=1∶5,则AC的长度是
cm.?
13.有一种落地晾衣架如图1所示,其原理是通过改变两根支撑杆夹角的度数来调整晾衣杆的高度.图2是支撑杆的平面示意图,AB和CD分别是两根不同长度的支撑杆,夹角∠BOD=α.若AO=85
cm,BO=DO=65
cm.问:当α=74°时,较长支撑杆的端点A离地面的高度h约为
cm.(参考数据:
sin
37°≈0.6,cos
37°≈0.8,sin
53°≈0.8,cos
53°≈0.6)?
三、解答题
14.如图,某幼儿园为了加强安全管理,决定将园内滑梯的倾斜角由45°降为30°,已知点D,B,C在同一水平地面上,且BD的长为2(-1)米,求改造后滑梯的长度.
15.如图,有一段斜坡BC的长为10米,坡角∠CBD=12°,为方便残疾人的轮椅车通行,现准备把坡角降为5°.
(1)求坡高CD;
(2)求斜坡新起点A与原起点B的距离.
(结果精确到0.1米,参考数据:sin
12°≈0.21,cos
12°≈0.98,tan
5°≈0.09)
16.某小区为了安全起见,决定将小区内的滑滑板的倾斜角由45°调为30°.如图,已知原滑滑板AB的长为4米,点D,B,C在同一水平地面上,调整后滑滑板会加长多少米?(结果精确到0.01米,参考数据:≈1.414,≈1.732,≈2.449)
17.如图,防洪大堤的横断面是梯形ABCD,其中AD∥BC,坡角α=60°,汛期来临前对其进行了加固,改造后的背水面坡角β=45°.若原坡长AB=20
m,求改造后的坡长AE.(结果保留根号)
18.如图1,水坝的横截面是梯形ABCD,∠ABC=37°,坝顶DC=3
m,背水坡AD的坡度i(即tan
∠DAB)为1∶0.5,坝底AB=14
m.
(1)求坝高;
(2)如图2,为了提高堤坝的防洪抗洪能力,防汛指挥部决定在背水坡将坝顶和坝底同时拓宽加固,使得AE=2DF,EF⊥BF,求DF的长.(参考数据:sin
37°≈,cos
37°≈,tan
37°≈)
参考答案
一、选择题
题号
1
2
3
4
5
答案
B
C
B
A
A
二、填空题
6. 1∶2
7. 110+20
8. 240
9. 39
10. 8 米
11. a ?
【提示】过点N作ND⊥MA,连接MN,易得△CMN为等边三角形,△ACM≌△DMN,∴DN=AM=a.
12. 270
13. 120
三、解答题
14.解:设AC=x,∴BC=AC=x,
∴tan
30°==,解得x=2,
∴AD=2AC=4.
答:改造后滑梯的长度为4米.
15.解:(1)在Rt△BCD中,CD=BC·sin
12°≈10×0.21=2.1(米).
(2)在Rt△BCD中,BD=BC·cos
12°≈10×0.98=9.8(米),
在Rt△ACD中,AD=≈23.33(米),
AB=AD-BD≈23.33-9.8=13.53≈13.5(米).
16.解:在Rt△ABC中,AC=AB·sin
45°=4×=2,在Rt△ADC中,AD=2AC=4,AD-AB=4-4≈1.66.
答:调整后滑滑板会加长约1.66米.
17.解:过点A作AF⊥BC于点F.
由题知,在Rt△ABF中,α=60°,
∴AF=AB·sin
60°=20×=10
(m).
在Rt△AEF中,β=45°,∴AE==10
(m).
答:改造后的坡长AE为10
m.
18.解:(1)作DM⊥AB于点M,CN⊥AB于点N.
由题意得tan
∠DAB==2.
设AM=x,∴DM=2x.
∵四边形DMNC是矩形,∴DM=CN=2x.
在Rt△NBC中,tan
37°=,
∴BN≈x.
∵x+3+x=14,∴x=3,∴DM=6.
答:坝高为6
m.
(2)作FH⊥AB于点H.设DF=y,∴AE=2y,EH=3+2y-y=3+y,BH=14+2y-(3+y)=11+y,
由△EFH∽△FBH,可得,
即,解得y=-7+2或-7-2(舍),
∴DF=2-7.
答:DF的长为(2-7)m.
