2020年秋沪科版九年级上册数学 期中检测卷(Word版 含答案)
文档属性
| 名称 | 2020年秋沪科版九年级上册数学 期中检测卷(Word版 含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 249.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-25 00:00:00 | ||
图片预览

文档简介
沪科版九年级上册数学检测卷
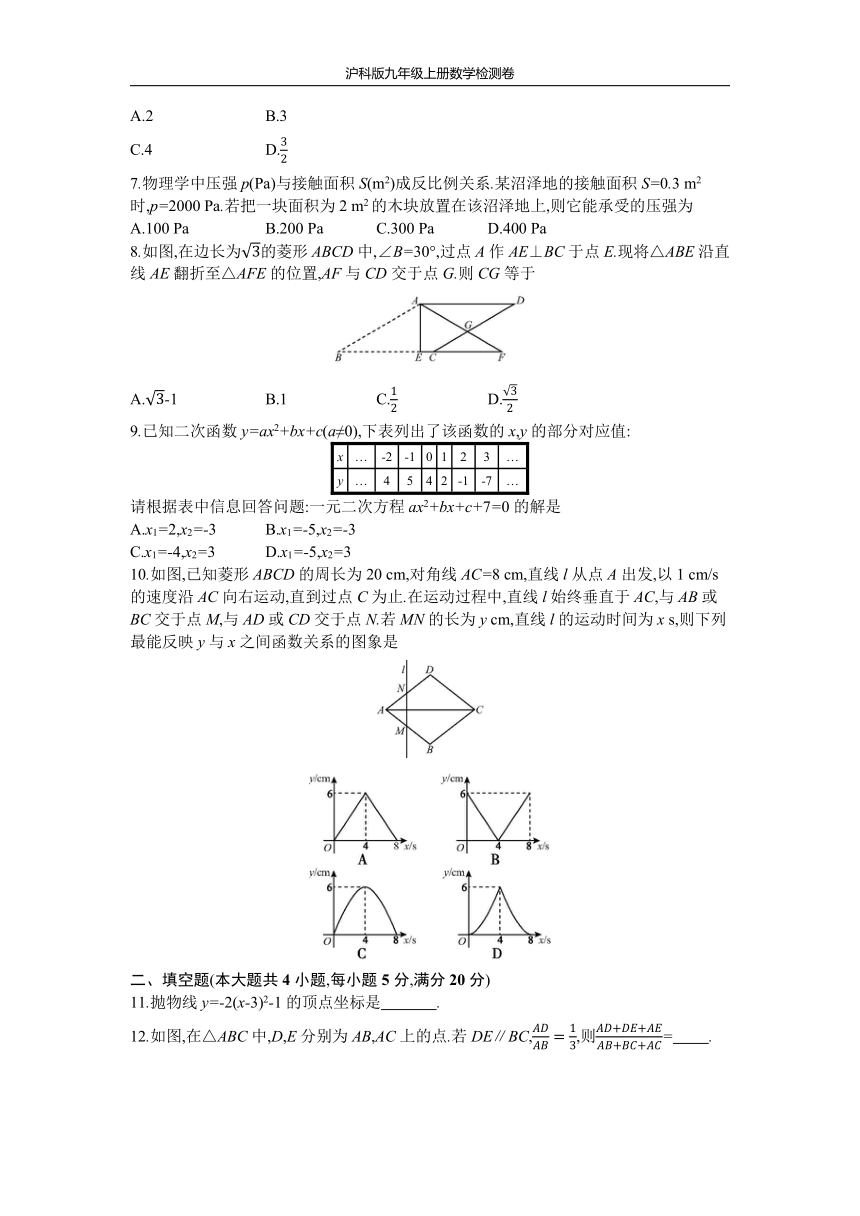
期中检测卷
(120分钟 150分)
题号
一
二
三
四
五
六
七
八
总分
得分
一、选择题(本大题共10小题,每小题4分,满分40分)
题 号
1
2
3
4
5
6
7
8
9
10
答 案
1.在比例尺是1∶40000的合肥市城区地图上,长江路的长度约为20
cm,则它的实际长度约为
A.8
km
B.4
km
C.2
km
D.800
m
2.如图,点P在反比例函数y=的图象上,过点P作PA⊥y轴于点A.若△OPA的面积为2,则k的值为
A.1
B.2
C.4
D.-4
3.若抛物线y=x2-4x-12与x轴交于点A,B,与y轴交于点C,则△ABC的面积为
A.24
B.36
C.48
D.96
4.为方便市民进行垃圾分类投放,某环保公司第一个月投放a个垃圾桶,计划第三个月投放垃圾桶y个.设该公司第二、三两个月投放垃圾桶数量的月平均增长率为x,那么y与x的函数关系是
A.y=a(1-x)2
B.y=a(1+x)2
C.y=(1-x)2+a
D.y=x2+a
5.如图,BD是四边形ABCD的对角线.若∠ABD=∠C=90°,则添加下列条件仍不能判定△ABD∽△DCB的是
A.AD∥BC
B.AD⊥CD
C.BD2=AD·BC
D.BD平分∠ADC
6.如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置.已知△ABC的面积为9,阴影部分三角形的面积为4.若AA'=1,则A'D等于
A.2
B.3
C.4
D.
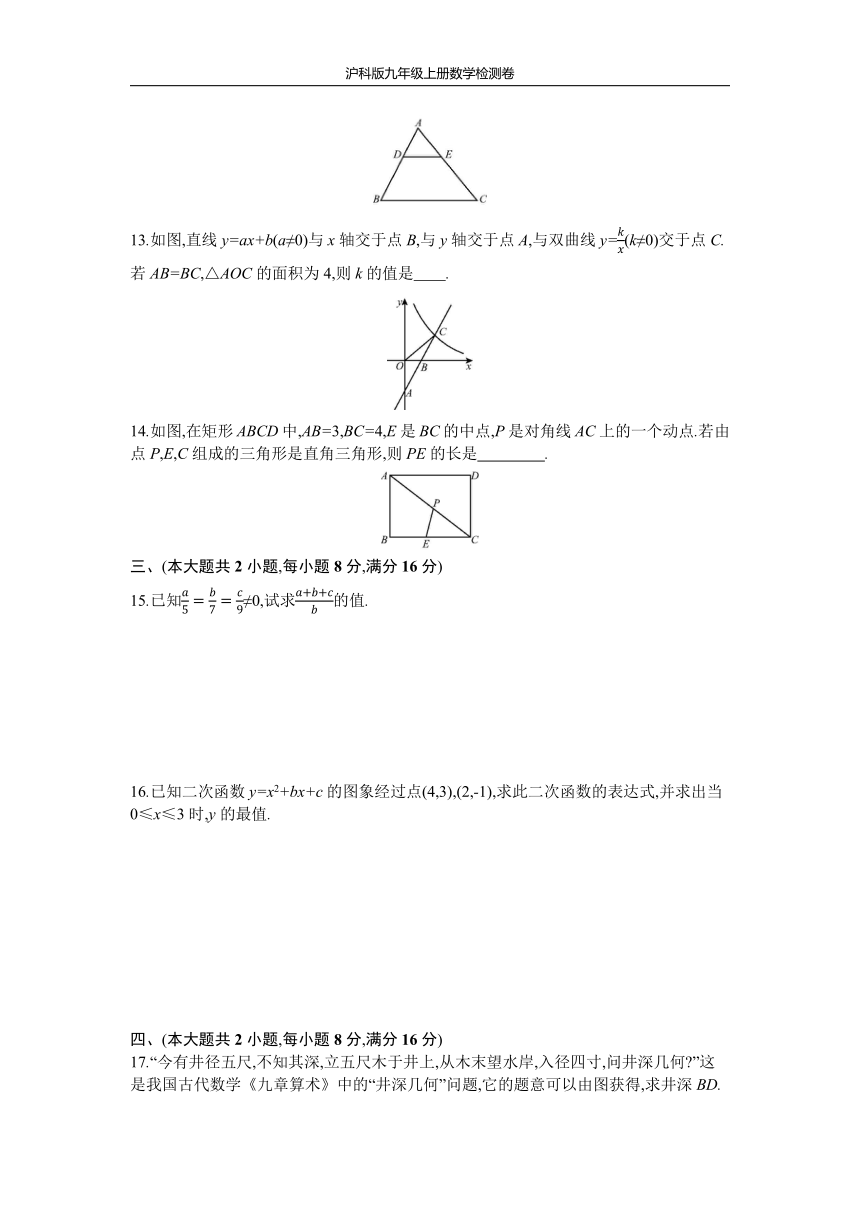
7.物理学中压强p(Pa)与接触面积S(m2)成反比例关系.某沼泽地的接触面积S=0.3
m2时,p=2000
Pa.若把一块面积为2
m2的木块放置在该沼泽地上,则它能承受的压强为
A.100
Pa
B.200
Pa
C.300
Pa
D.400
Pa
8.如图,在边长为的菱形ABCD中,∠B=30°,过点A作AE⊥BC于点E.现将△ABE沿直线AE翻折至△AFE的位置,AF与CD交于点G.则CG等于
A.-1
B.1
C.
D.
9.已知二次函数y=ax2+bx+c(a≠0),下表列出了该函数的x,y的部分对应值:
x
…
-2
-1
0
1
2
3
…
y
…
4
5
4
2
-1
-7
…
请根据表中信息回答问题:一元二次方程ax2+bx+c+7=0的解是
A.x1=2,x2=-3
B.x1=-5,x2=-3
C.x1=-4,x2=3
D.x1=-5,x2=3
10.如图,已知菱形ABCD的周长为20
cm,对角线AC=8
cm,直线l从点A出发,以1
cm/s的速度沿AC向右运动,直到过点C为止.在运动过程中,直线l始终垂直于AC,与AB或BC交于点M,与AD或CD交于点N.若MN的长为y
cm,直线l的运动时间为x
s,则下列最能反映y与x之间函数关系的图象是
二、填空题(本大题共4小题,每小题5分,满分20分)
11.抛物线y=-2(x-3)2-1的顶点坐标是
.?
12.如图,在△ABC中,D,E分别为AB,AC上的点.若DE∥BC,,则=?
.?
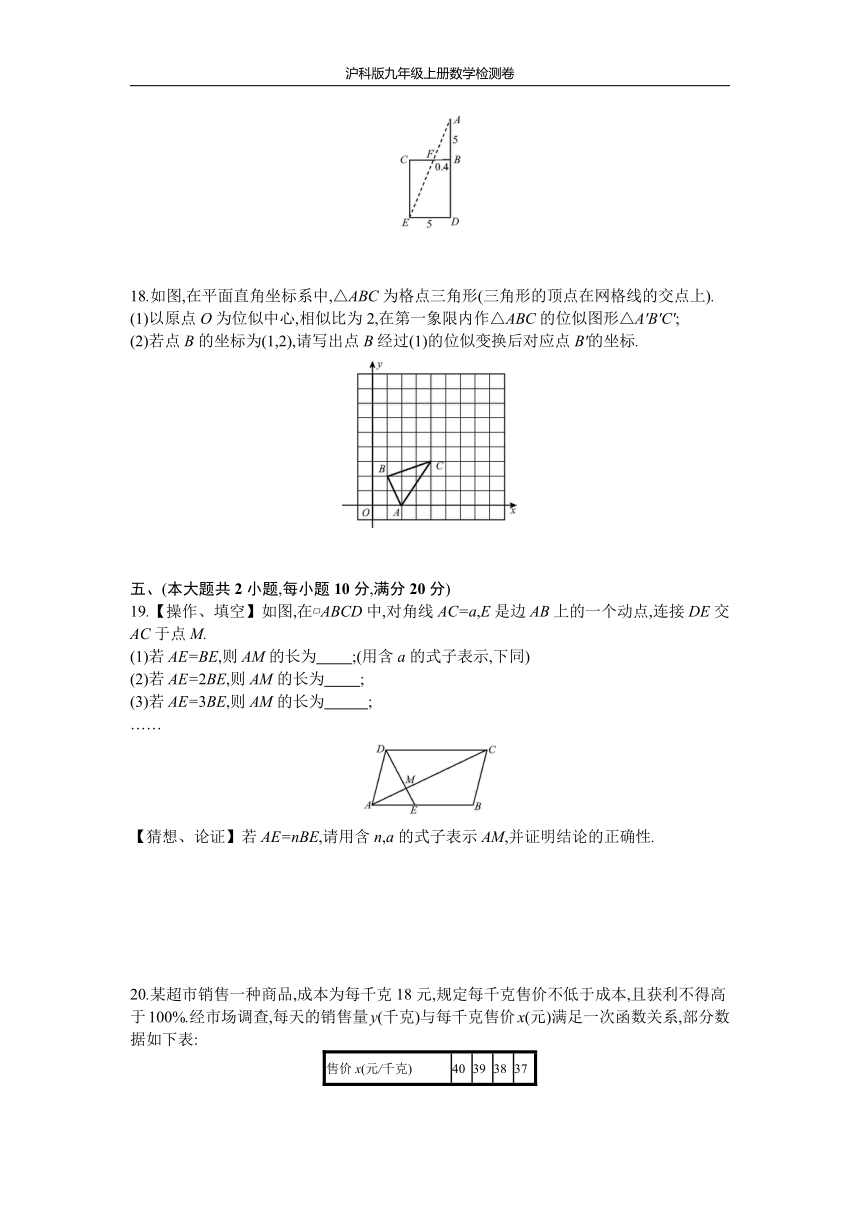
13.如图,直线y=ax+b(a≠0)与x轴交于点B,与y轴交于点A,与双曲线y=(k≠0)交于点C.若AB=BC,△AOC的面积为4,则k的值是 .?
14.如图,在矩形ABCD中,AB=3,BC=4,E是BC的中点,P是对角线AC上的一个动点.若由点P,E,C组成的三角形是直角三角形,则PE的长是?
.?
三、(本大题共2小题,每小题8分,满分16分)
15.已知≠0,试求的值.
16.已知二次函数y=x2+bx+c的图象经过点(4,3),(2,-1),求此二次函数的表达式,并求出当0≤x≤3时,y的最值.
四、(本大题共2小题,每小题8分,满分16分)
17.“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,求井深BD.
18.如图,在平面直角坐标系中,△ABC为格点三角形(三角形的顶点在网格线的交点上).
(1)以原点O为位似中心,相似比为2,在第一象限内作△ABC的位似图形△A'B'C';
(2)若点B的坐标为(1,2),请写出点B经过(1)的位似变换后对应点B'的坐标.
五、(本大题共2小题,每小题10分,满分20分)
19.【操作、填空】如图,在?ABCD中,对角线AC=a,E是边AB上的一个动点,连接DE交AC于点M.
(1)若AE=BE,则AM的长为?
;(用含a的式子表示,下同)?
(2)若AE=2BE,则AM的长为?
;?
(3)若AE=3BE,则AM的长为?
;?
……
【猜想、论证】若AE=nBE,请用含n,a的式子表示AM,并证明结论的正确性.
20.某超市销售一种商品,成本为每千克18元,规定每千克售价不低于成本,且获利不得高于100%.经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克)
40
39
38
37
销售量y(千克)
20
22
24
26
(1)求y与x之间的函数关系式;
(2)设该商品每天的总利润为W元,求W与x之间的函数关系式(利润=收入-成本),并指出售价为多少时获得最大利润,最大利润是多少?
六、(本题满分12分)
21.如图,在平面直角坐标系中,一次函数y=-3x+6的图象与x轴、y轴分别交于A,B两点.以AB为边在第一象限内作正方形ABCD,若反比例函数y=(k≠0)的图象经过顶点D.
(1)试确定k的值;
(2)若正方形ABCD向左平移n个单位后,顶点C恰好落在反比例函数y=的图象上,试确定n的值.
七、(本题满分12分)
22.如图,在Rt△ABC中,∠C=90°,∠ABC和∠BAC的平分线相交于点D,过点D作PQ∥AB交BC于点Q,交AC于点P.
(1)求证:PQ=AP+BQ;
(2)若∠CAB=45°,求证:BD2=BQ·BA;
(3)若AB=5,BC=4,求AP的长.
八、(本题满分14分)
23.已知抛物线y=2x2+8x+6与x轴交于点A,B(点A在点B的左侧),与y轴交于点C.
(1)求点A,C的坐标.
(2)我们规定对于直线l1:y=k1x+b1,直线l2:y=k2x+b2,若k1·k2=-1,则直线l1⊥l2;反过来也成立.请根据这个规定解决下列问题:
①直线y=-3x+与直线y=x-4是否垂直?并说明理由.
②若P是抛物线y=2x2+8x+6对称轴上的一个动点,是否存在点P与点A、点C构成以AC为直角边的直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
参考答案
一、选择题(本大题共10小题,每小题4分,满分40分)
题 号
1
2
3
4
5
6
7
8
9
10
答 案
A
C
C
B
D
A
C
A
D
A
二、填空题(本大题共4小题,每小题5分,满分20分)
11. (3,-1)
12.?
13. 8
14.?
三、(本大题共2小题,每小题8分,满分16分)
15.解:∵,∴,∴=3.
16.解:∵二次函数y=x2+bx+c的图象经过点(4,3),(2,-1),
∴解得
∴该函数的表达式为y=x2-4x+3.
∴在0≤x≤3范围内,当x=0时,y取得最大值3;当x=2时,y取得最小值-1.
四、(本大题共2小题,每小题8分,满分16分)
17.解:依题意可得△ABF∽△ADE,
∴AB∶AD=BF∶DE,即5∶AD=0.4∶5,解得AD=62.5,
∴BD=AD-AB=62.5-5=57.5(尺),
∴井深BD为57.5尺.
18.解:(1)图略.
(2)点B'的坐标为(2,4).
五、(本大题共2小题,每小题10分,满分20分)
19.解:
(1)?a ?(2)?a
(3)?a
【猜想、论证】AM=a.
证明:∵AE=nBE,∴.∵ABCD为平行四边形,∴AB=CD,∴.∵AB∥CD,∴△AEM∽△CDM,∴,∴AM=a=a,∴结论正确.
20.解:(1)设y与x之间的函数关系式为y=kx+b,
由题意得解得
∴y与x之间的函数关系式为y=-2x+100(18≤x≤36).
(2)由题意得W=(x-18)y=(x-18)(-2x+100)=-2x2+136x-1800=-2(x-34)2+512,
∴当x=34时利润最大,为512元.此时<100%,符合题意.
答:售价为34元/千克时获得最大利润,最大利润是512元.
六、(本题满分12分)
21.解:(1)易得点A的坐标为(2,0),点B的坐标为(0,6).
过点D作x轴的垂线,垂足为G,∴∠BOA=∠AGD=90°.
∵正方形ABCD中,AB=DA,∠BAD=90°,
∴∠BAO+∠DAG=90°.
∵∠ABO+∠BAO=90°,∴∠ABO=∠DAG,∴△ABO≌△DAG,
∴GD=OA=2,GA=OB=6,∴点D的坐标为(8,2).
∵反比例函数y=(k≠0)的图象经过顶点D,∴2=,∴k=16.
(2)过点C作y轴的垂线,垂足为E,交双曲线于点F.
由(1)易证△ABO≌△BCE,∴BE=OA=2,CE=OB=6,
∴C(6,8).
对于y=,当y=8时,x=2,∴点F的坐标为(2,8),
∴n=CF=CE-EF=6-2=4.
七、(本题满分12分)
22.解:(1)∵BD平分∠CBA,∴∠DBA=∠DBQ.
∵PQ∥AB,∴∠DBA=∠BDQ,∴∠DBQ=∠BDQ,∴BQ=DQ.
同理PD=AP,∴PQ=PD+DQ=AP+BQ.
(2)∵PQ∥AB,∴∠QPC=∠BAC=45°,∴∠BQD=90°+45°=135°.
∵BD平分∠CBA,AD平分∠CAB,∴∠DBA=∠CBA,∠DAB=∠CAB,∴∠DBA+∠DAB=(∠CBA+∠CAB)=45°,
∴∠BDA=135°,∴∠BQD=∠BDA.
∵∠DBA=∠DBQ,∴△BQD∽△BDA,∴,
∴BD2=BQ·BA.
(3)由(1)得PA=PD,DQ=BQ.
∵PQ∥AB,∴△CPQ∽△CAB,∴.
设AP=x,BQ=y,∴,解得x=,∴AP的长为.
八、(本题满分14分)
23.解:(1)点A的坐标为(-3,0),点C的坐标为(0,6).
(2)①∵-3×=-1,
∴直线y=-3x+与直线y=x-4相互垂直.
②存在.
∵-=-2,∴抛物线y=2x2+8x+6的对称轴为直线x=-2.
设直线AC:y=kx+b,根据题意得解得∴直线AC的函数表达式为y=2x+6.
分两种情况:当PA⊥AC时,根据新定义可设PA:y=-x+m.∵点A的坐标为(-3,0),∴0=-×(-3)+m,解得m=-,∴直线PA为y=-x-.当x=-2时,y=-×(-2)-=-,此时点P的坐标为;当PC⊥AC时,根据新定义可设PC:y=-x+n,∵点C的坐标为(0,6),∴6=-×0+m,解得m=6,∴直线PA为y=-x+6.当x=-2时,y=-×(-2)+6=7,此时点P的坐标为(-2,7).
综上,点P的坐标为或(-2,7).
期中检测卷
(120分钟 150分)
题号
一
二
三
四
五
六
七
八
总分
得分
一、选择题(本大题共10小题,每小题4分,满分40分)
题 号
1
2
3
4
5
6
7
8
9
10
答 案
1.在比例尺是1∶40000的合肥市城区地图上,长江路的长度约为20
cm,则它的实际长度约为
A.8
km
B.4
km
C.2
km
D.800
m
2.如图,点P在反比例函数y=的图象上,过点P作PA⊥y轴于点A.若△OPA的面积为2,则k的值为
A.1
B.2
C.4
D.-4
3.若抛物线y=x2-4x-12与x轴交于点A,B,与y轴交于点C,则△ABC的面积为
A.24
B.36
C.48
D.96
4.为方便市民进行垃圾分类投放,某环保公司第一个月投放a个垃圾桶,计划第三个月投放垃圾桶y个.设该公司第二、三两个月投放垃圾桶数量的月平均增长率为x,那么y与x的函数关系是
A.y=a(1-x)2
B.y=a(1+x)2
C.y=(1-x)2+a
D.y=x2+a
5.如图,BD是四边形ABCD的对角线.若∠ABD=∠C=90°,则添加下列条件仍不能判定△ABD∽△DCB的是
A.AD∥BC
B.AD⊥CD
C.BD2=AD·BC
D.BD平分∠ADC
6.如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置.已知△ABC的面积为9,阴影部分三角形的面积为4.若AA'=1,则A'D等于
A.2
B.3
C.4
D.
7.物理学中压强p(Pa)与接触面积S(m2)成反比例关系.某沼泽地的接触面积S=0.3
m2时,p=2000
Pa.若把一块面积为2
m2的木块放置在该沼泽地上,则它能承受的压强为
A.100
Pa
B.200
Pa
C.300
Pa
D.400
Pa
8.如图,在边长为的菱形ABCD中,∠B=30°,过点A作AE⊥BC于点E.现将△ABE沿直线AE翻折至△AFE的位置,AF与CD交于点G.则CG等于
A.-1
B.1
C.
D.
9.已知二次函数y=ax2+bx+c(a≠0),下表列出了该函数的x,y的部分对应值:
x
…
-2
-1
0
1
2
3
…
y
…
4
5
4
2
-1
-7
…
请根据表中信息回答问题:一元二次方程ax2+bx+c+7=0的解是
A.x1=2,x2=-3
B.x1=-5,x2=-3
C.x1=-4,x2=3
D.x1=-5,x2=3
10.如图,已知菱形ABCD的周长为20
cm,对角线AC=8
cm,直线l从点A出发,以1
cm/s的速度沿AC向右运动,直到过点C为止.在运动过程中,直线l始终垂直于AC,与AB或BC交于点M,与AD或CD交于点N.若MN的长为y
cm,直线l的运动时间为x
s,则下列最能反映y与x之间函数关系的图象是
二、填空题(本大题共4小题,每小题5分,满分20分)
11.抛物线y=-2(x-3)2-1的顶点坐标是
.?
12.如图,在△ABC中,D,E分别为AB,AC上的点.若DE∥BC,,则=?
.?
13.如图,直线y=ax+b(a≠0)与x轴交于点B,与y轴交于点A,与双曲线y=(k≠0)交于点C.若AB=BC,△AOC的面积为4,则k的值是 .?
14.如图,在矩形ABCD中,AB=3,BC=4,E是BC的中点,P是对角线AC上的一个动点.若由点P,E,C组成的三角形是直角三角形,则PE的长是?
.?
三、(本大题共2小题,每小题8分,满分16分)
15.已知≠0,试求的值.
16.已知二次函数y=x2+bx+c的图象经过点(4,3),(2,-1),求此二次函数的表达式,并求出当0≤x≤3时,y的最值.
四、(本大题共2小题,每小题8分,满分16分)
17.“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,求井深BD.
18.如图,在平面直角坐标系中,△ABC为格点三角形(三角形的顶点在网格线的交点上).
(1)以原点O为位似中心,相似比为2,在第一象限内作△ABC的位似图形△A'B'C';
(2)若点B的坐标为(1,2),请写出点B经过(1)的位似变换后对应点B'的坐标.
五、(本大题共2小题,每小题10分,满分20分)
19.【操作、填空】如图,在?ABCD中,对角线AC=a,E是边AB上的一个动点,连接DE交AC于点M.
(1)若AE=BE,则AM的长为?
;(用含a的式子表示,下同)?
(2)若AE=2BE,则AM的长为?
;?
(3)若AE=3BE,则AM的长为?
;?
……
【猜想、论证】若AE=nBE,请用含n,a的式子表示AM,并证明结论的正确性.
20.某超市销售一种商品,成本为每千克18元,规定每千克售价不低于成本,且获利不得高于100%.经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克)
40
39
38
37
销售量y(千克)
20
22
24
26
(1)求y与x之间的函数关系式;
(2)设该商品每天的总利润为W元,求W与x之间的函数关系式(利润=收入-成本),并指出售价为多少时获得最大利润,最大利润是多少?
六、(本题满分12分)
21.如图,在平面直角坐标系中,一次函数y=-3x+6的图象与x轴、y轴分别交于A,B两点.以AB为边在第一象限内作正方形ABCD,若反比例函数y=(k≠0)的图象经过顶点D.
(1)试确定k的值;
(2)若正方形ABCD向左平移n个单位后,顶点C恰好落在反比例函数y=的图象上,试确定n的值.
七、(本题满分12分)
22.如图,在Rt△ABC中,∠C=90°,∠ABC和∠BAC的平分线相交于点D,过点D作PQ∥AB交BC于点Q,交AC于点P.
(1)求证:PQ=AP+BQ;
(2)若∠CAB=45°,求证:BD2=BQ·BA;
(3)若AB=5,BC=4,求AP的长.
八、(本题满分14分)
23.已知抛物线y=2x2+8x+6与x轴交于点A,B(点A在点B的左侧),与y轴交于点C.
(1)求点A,C的坐标.
(2)我们规定对于直线l1:y=k1x+b1,直线l2:y=k2x+b2,若k1·k2=-1,则直线l1⊥l2;反过来也成立.请根据这个规定解决下列问题:
①直线y=-3x+与直线y=x-4是否垂直?并说明理由.
②若P是抛物线y=2x2+8x+6对称轴上的一个动点,是否存在点P与点A、点C构成以AC为直角边的直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
参考答案
一、选择题(本大题共10小题,每小题4分,满分40分)
题 号
1
2
3
4
5
6
7
8
9
10
答 案
A
C
C
B
D
A
C
A
D
A
二、填空题(本大题共4小题,每小题5分,满分20分)
11. (3,-1)
12.?
13. 8
14.?
三、(本大题共2小题,每小题8分,满分16分)
15.解:∵,∴,∴=3.
16.解:∵二次函数y=x2+bx+c的图象经过点(4,3),(2,-1),
∴解得
∴该函数的表达式为y=x2-4x+3.
∴在0≤x≤3范围内,当x=0时,y取得最大值3;当x=2时,y取得最小值-1.
四、(本大题共2小题,每小题8分,满分16分)
17.解:依题意可得△ABF∽△ADE,
∴AB∶AD=BF∶DE,即5∶AD=0.4∶5,解得AD=62.5,
∴BD=AD-AB=62.5-5=57.5(尺),
∴井深BD为57.5尺.
18.解:(1)图略.
(2)点B'的坐标为(2,4).
五、(本大题共2小题,每小题10分,满分20分)
19.解:
(1)?a ?(2)?a
(3)?a
【猜想、论证】AM=a.
证明:∵AE=nBE,∴.∵ABCD为平行四边形,∴AB=CD,∴.∵AB∥CD,∴△AEM∽△CDM,∴,∴AM=a=a,∴结论正确.
20.解:(1)设y与x之间的函数关系式为y=kx+b,
由题意得解得
∴y与x之间的函数关系式为y=-2x+100(18≤x≤36).
(2)由题意得W=(x-18)y=(x-18)(-2x+100)=-2x2+136x-1800=-2(x-34)2+512,
∴当x=34时利润最大,为512元.此时<100%,符合题意.
答:售价为34元/千克时获得最大利润,最大利润是512元.
六、(本题满分12分)
21.解:(1)易得点A的坐标为(2,0),点B的坐标为(0,6).
过点D作x轴的垂线,垂足为G,∴∠BOA=∠AGD=90°.
∵正方形ABCD中,AB=DA,∠BAD=90°,
∴∠BAO+∠DAG=90°.
∵∠ABO+∠BAO=90°,∴∠ABO=∠DAG,∴△ABO≌△DAG,
∴GD=OA=2,GA=OB=6,∴点D的坐标为(8,2).
∵反比例函数y=(k≠0)的图象经过顶点D,∴2=,∴k=16.
(2)过点C作y轴的垂线,垂足为E,交双曲线于点F.
由(1)易证△ABO≌△BCE,∴BE=OA=2,CE=OB=6,
∴C(6,8).
对于y=,当y=8时,x=2,∴点F的坐标为(2,8),
∴n=CF=CE-EF=6-2=4.
七、(本题满分12分)
22.解:(1)∵BD平分∠CBA,∴∠DBA=∠DBQ.
∵PQ∥AB,∴∠DBA=∠BDQ,∴∠DBQ=∠BDQ,∴BQ=DQ.
同理PD=AP,∴PQ=PD+DQ=AP+BQ.
(2)∵PQ∥AB,∴∠QPC=∠BAC=45°,∴∠BQD=90°+45°=135°.
∵BD平分∠CBA,AD平分∠CAB,∴∠DBA=∠CBA,∠DAB=∠CAB,∴∠DBA+∠DAB=(∠CBA+∠CAB)=45°,
∴∠BDA=135°,∴∠BQD=∠BDA.
∵∠DBA=∠DBQ,∴△BQD∽△BDA,∴,
∴BD2=BQ·BA.
(3)由(1)得PA=PD,DQ=BQ.
∵PQ∥AB,∴△CPQ∽△CAB,∴.
设AP=x,BQ=y,∴,解得x=,∴AP的长为.
八、(本题满分14分)
23.解:(1)点A的坐标为(-3,0),点C的坐标为(0,6).
(2)①∵-3×=-1,
∴直线y=-3x+与直线y=x-4相互垂直.
②存在.
∵-=-2,∴抛物线y=2x2+8x+6的对称轴为直线x=-2.
设直线AC:y=kx+b,根据题意得解得∴直线AC的函数表达式为y=2x+6.
分两种情况:当PA⊥AC时,根据新定义可设PA:y=-x+m.∵点A的坐标为(-3,0),∴0=-×(-3)+m,解得m=-,∴直线PA为y=-x-.当x=-2时,y=-×(-2)-=-,此时点P的坐标为;当PC⊥AC时,根据新定义可设PC:y=-x+n,∵点C的坐标为(0,6),∴6=-×0+m,解得m=6,∴直线PA为y=-x+6.当x=-2时,y=-×(-2)+6=7,此时点P的坐标为(-2,7).
综上,点P的坐标为或(-2,7).
同课章节目录
