2020年秋沪科版九年级上册数学 期末检测卷一(Word版 含答案)
文档属性
| 名称 | 2020年秋沪科版九年级上册数学 期末检测卷一(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 265.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-25 10:20:53 | ||
图片预览


文档简介
沪科版九年级上册数学检测卷
期末检测卷一
(120分钟 150分)
题号
一
二
三
四
五
六
七
八
总分
得分
一、选择题(本大题共10小题,每小题4分,满分40分)
题 号
1
2
3
4
5
6
7
8
9
10
答 案
1.若sin
(x-10)°=,则锐角x的度数是
A.20°
B.30°
C.40°
D.70°
2.反比例函数y=的图象分布在第二、四象限,则k的取值范围是
A.k<
B.k<
C.k>
D.k>
3.把二次函数y=x2-4x+3配方成y=a(x+h)2+m的形式,则h,m的值分别是
A.2,-1
B.-2,-1
C.-2,1
D.-1,-2
4.已知△ABC与△DEF相似,且面积的比为1∶4,则△ABC与△DEF对应中线的比为
A.1∶16
B.1∶4
C.1∶2
D.2∶1
5.若锐角α满足α<,则下列结论正确的是
A.0°<α<30°
B.30°<α<45°
C.45°<α<60°
D.0°<α<45°
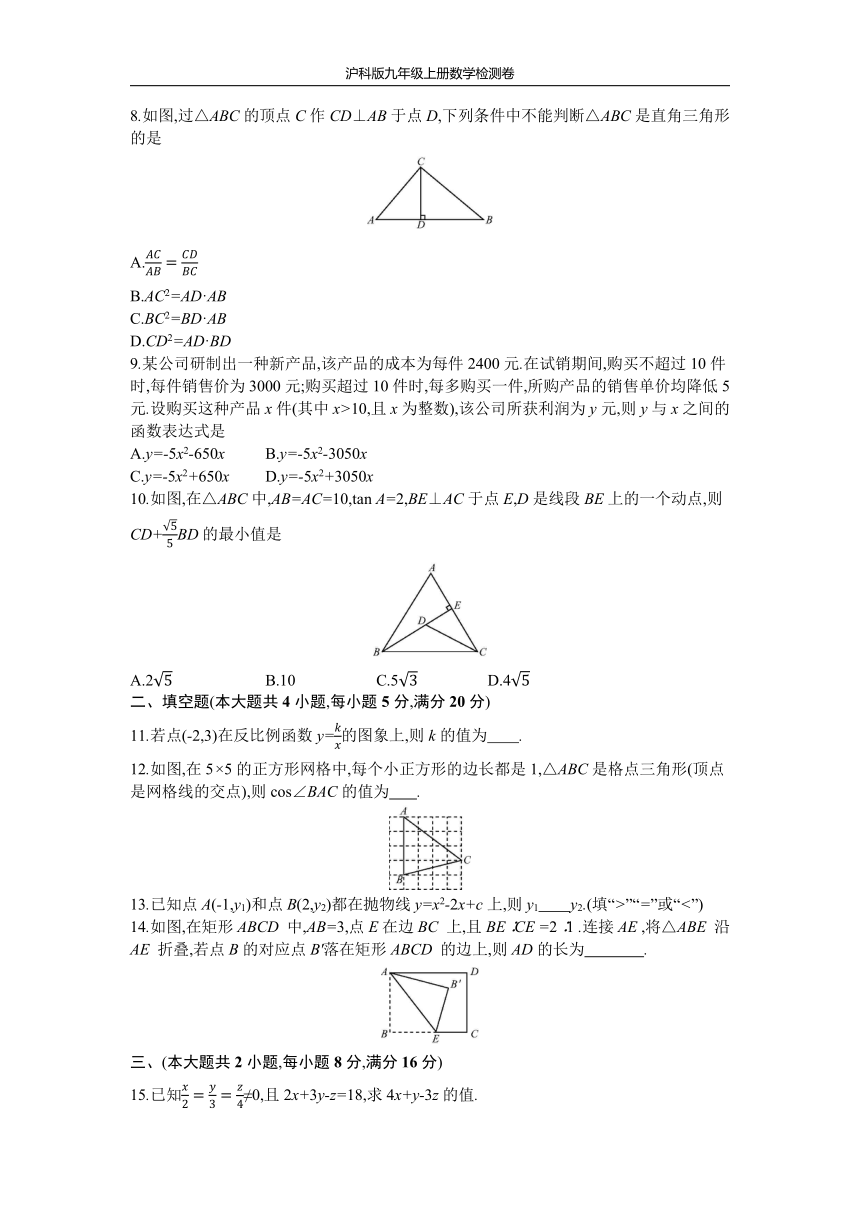
6.如图,线段AB两个端点的坐标分别为A(2.5,5)和B(5,0).以原点为位似中心,将线段AB缩小得到线段CD.若点D的坐标为(2,0),则点C的坐标为
A.(1,2)
B.(1,2.5)
C.(1.25,2.5)
D.(1.5,3)
7.已知二次函数y=ax2+bx+c与一次函数y=mx+n(a,m≠0)的图象如图所示,则关于x的一元二次方程ax2+(b-m)x+c-n=0的根的情况是
A.有两个相等的实数根
B.有两个不相等的实数根
C.没有实数根
D.无法确定
8.如图,过△ABC的顶点C作CD⊥AB于点D,下列条件中不能判断△ABC是直角三角形的是
A.
B.AC2=AD·AB
C.BC2=BD·AB
D.CD2=AD·BD
9.某公司研制出一种新产品,该产品的成本为每件2400元.在试销期间,购买不超过10件时,每件销售价为3000元;购买超过10件时,每多购买一件,所购产品的销售单价均降低5元.设购买这种产品x件(其中x>10,且x为整数),该公司所获利润为y元,则y与x之间的函数表达式是
A.y=-5x2-650x
B.y=-5x2-3050x
C.y=-5x2+650x
D.y=-5x2+3050x
10.如图,在△ABC中,AB=AC=10,tan
A=2,BE⊥AC于点E,D是线段BE上的一个动点,则CD+BD的最小值是
A.2
B.10
C.5
D.4
二、填空题(本大题共4小题,每小题5分,满分20分)
11.若点(-2,3)在反比例函数y=的图象上,则k的值为 .?
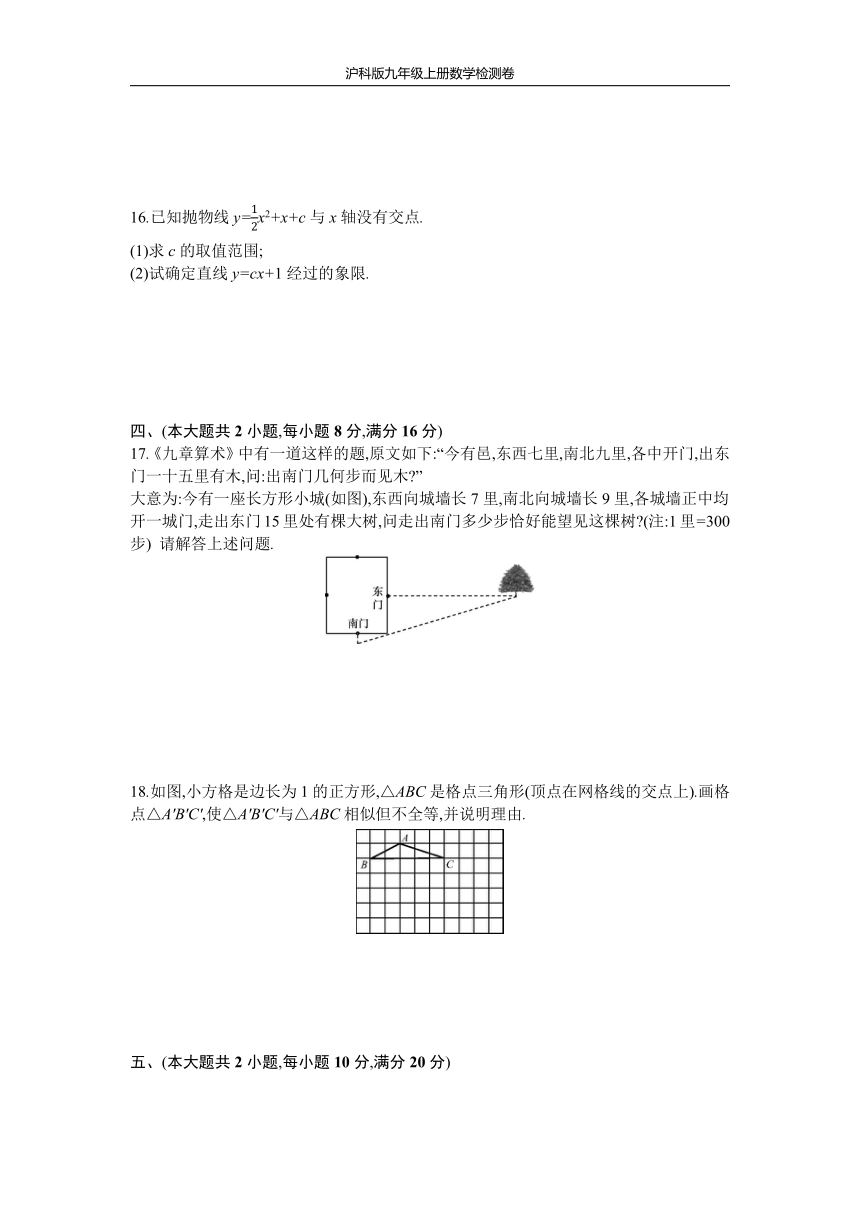
12.如图,在5×5的正方形网格中,每个小正方形的边长都是1,△ABC是格点三角形(顶点是网格线的交点),则cos∠BAC的值为?
.?
13.已知点A(-1,y1)和点B(2,y2)都在抛物线y=x2-2x+c上,则y1 y2.(填“>”“=”或“<”)?
14.如图,在矩形ABCD
中,AB=3,点E在边BC
上,且BE∶CE
=2∶1
.连接AE
,将△ABE
沿AE
折叠,若点B的对应点B'落在矩形ABCD
的边上,则AD的长为?
.?
三、(本大题共2小题,每小题8分,满分16分)
15.已知≠0,且2x+3y-z=18,求4x+y-3z的值.
16.已知抛物线y=x2+x+c与x轴没有交点.
(1)求c的取值范围;
(2)试确定直线y=cx+1经过的象限.
四、(本大题共2小题,每小题8分,满分16分)
17.《九章算术》中有一道这样的题,原文如下:“今有邑,东西七里,南北九里,各中开门,出东门一十五里有木,问:出南门几何步而见木?”
大意为:今有一座长方形小城(如图),东西向城墙长7里,南北向城墙长9里,各城墙正中均开一城门,走出东门15里处有棵大树,问走出南门多少步恰好能望见这棵树?(注:1里=300步)
请解答上述问题.
18.如图,小方格是边长为1的正方形,△ABC是格点三角形(顶点在网格线的交点上).画格点△A'B'C',使△A'B'C'与△ABC相似但不全等,并说明理由.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,游客从离水平地面1400米高的A处坐缆车出发,沿俯角为60°的方向滑行1000米到达D处,再沿俯角为30°的方向滑行到山脚C处,求水平距离BC的长.(结果保留整数,参考数据:≈1.73)
20.我们规定:对于锐角α,β有下列三角函数关系,sin
(α±β)=sin
αcos
β±cos
αsin
β;cos
(α±β)=cos
αcos
β?sin
αsin
β.根据这个规定,解答下列问题:
(1)求sin
105°的值;
(2)求cos
15°的值.(结果保留根号)
六、(本题满分12分)
21.如图,已知直线y=ax+b与x轴交于点A(-2,0),与y轴交于点B(0,1),与反比例函数y=(x>0)交于点C(1,m).
(1)求m的值,并确定一次函数与反比例函数的表达式;
(2)经过点D且垂直于x轴的直线与直线y=ax+b交于点P,与反比例函数y=(x>0)的图象交于点Q.若AB∶AP=1∶3,求△APQ的面积.
七、(本题满分12分)
22.如图,直线y=kx+b(k,b为常数)分别与x轴、y轴交于点C(-3,0),D(0,3),抛物线y=-x2+x+2与x轴交于点A和点B(点A在点B的左侧).
(1)求直线y=kx+b的表达式;
(2)求点A和点B的坐标;
(3)若直线l与x轴垂直,在点A与点B之间移动,且与直线y=kx+b(k,b为常数)交于点E,与抛物线y=-x2+x+2交于点F,求EF的最小值.
八、(本题满分14分)
23.已知四边形ABCD的一组对边AD,BC的延长线相交于点E.
(1)如图1,若∠ABC=∠ADC=90°,求证:ED·EA=EC·EB;
(2)如图2,若∠ABC=120°,cos
∠ADC=,CD=5,AB=12,△CDE的面积为6,求四边形ABCD的面积;
(3)如图3,另一组对边AB,DC的延长线相交于点F.若cos∠ABC=cos∠ADC=,CD=5,CF=ED=n,直接写出AD的长.(用含n的式子表示)
参考答案
一、选择题(本大题共10小题,每小题4分,满分40分)
题 号
1
2
3
4
5
6
7
8
9
10
答 案
C
D
B
C
B
A
B
A
C
D
10.【提示】作DH⊥AB于点H,
CM⊥AB于点M.∴易得AE=2,BE=4.∵AB=AC,BE⊥AC,
CM⊥AB,∴
CM=BE=4(等腰三角形两腰上的高相等).易知DH=BD,∴CD+BD=CD+DH.∵CD+DH≥CM,∴CD+BD≥4,∴CD+BD的最小值为4.
二、填空题(本大题共4小题,每小题5分,满分20分)
11. -6
12.?
13. >
14.?
【提示】设BC=AD=x,∵BE∶CE
=2∶1,∴BE=x,CE=x.由折叠的性质得,AB=A
B'=3,
∠B'=∠B=90°,BE=
B'E=x.由题意可得,点B'的位置有两种情况:①当点B'落在矩形的边AD上时,则四边形ABEB'为正方形,∴B'E=AB=BE=3,则x=3,∴x=;②当点B'落在边CD上时,由已知可得BE=B'E=x,EC=x.易得△AB'D∽△B'EC,∴,∴DB'=AB'=.在Rt△ADB'中,由勾股定理可得AD=.综上所述,AD的长为.
三、(本大题共2小题,每小题8分,满分16分)
15.解:设=k,可得x=2k,y=3k,z=4k,
代入2x+3y-z=18中,得4k+9k-4k=18,解得k=2,
所以x=4,y=6,z=8,
所以4x+y-3z=16+6-24=-2.
16.解:(1)c>.
(2)直线y=cx+1经过第一、二、三象限.
四、(本大题共2小题,每小题8分,满分16分)
17.解:由题意,得AB=15里,AC=4.5里,CD=3.5里,
∵DE⊥CD,AC⊥CD,∴AC∥DE,∴△ACB∽△DEC,
∴,即,解得DE=1.05(里)=315步,
∴走出南门315步恰好能望见这棵树.
18.
解:如图所示.(本题答案不唯一)
理由:由勾股定理得AB=,AC=,BC=5,A'B'=,B'C'=,A'C'=2,∴,∴△ABC∽△A'B'C'.
五、(本大题共2小题,每小题10分,满分20分)
19.解:过点D作DE⊥AB于点E,DF⊥BC于点F.
由题意知∠DAE=30°,∴DE=AD=×1000=500,在Rt△ADE中,AE==500,
∴DF=AB-AE=1400-500.
在Rt△DFC中,CF=(1400-500)=1400-1500,∴BC=DE+CF=500+1400-1500=1400-1000≈1422(米).
20.解:(1)sin
105°=sin
(45°+60°)=sin
45°cos
60°+cos
45°sin
60°=.
(2)cos
15°=cos
(45°-30°)=cos
45°cos
30°+sin
45°sin
30°=.
六、(本题满分12分)
21.解:(1)∵直线y=ax+b经过点A(-2,0),点B(0,1),
∴解得∴一次函数的表达式为y=x+1.
∵点C(1,m)在直线y=x+1上,∴m=+1=.
∵点C在反比例函数y=(k>0)的图象上,
∴k=,∴反比例函数的表达式为y=.
(2)∵BO⊥AD,PD⊥AD,∴BO∥PD,∴.
∵AB∶AP=1∶3,AO=2,∴OD=2AO=4,∴点D的坐标为(4,0),
∴点P的坐标为(4,3),点Q的坐标为(4,).
∴△APQ的面积=.
七、(本题满分12分)
22.解:(1)易得直线的表达式是y=x+3.
(2)点A的坐标为(-1,0),点B的坐标为(3,0).
(3)令点E,F的横坐标为a,EF=s,则点F的纵坐标为-a2+a+2,点E的纵坐标为a+3,所以s=(a+3)-a2-a+1(-10,所以抛物线的开口向上,又-1所以当a=时,s有最小值,且最小值为,即EF的最小值为.
八、(本题满分14分)
23.解:(1)略.
(2)过点C作CF⊥AD于点F,过点A作AG⊥EB交EB的延长线于点G.
在Rt△CDF中,cos
∠ADC=,又∵CD=5,∴DF=3,∴CF==4.
∵S△CDE=6,
∴ED·CF=6,∴ED=3,∴EF=ED+DF=6.
∵∠ABC=120°,∠G=90°,∴∠BAG=30°.
在Rt△ABG中,BG=AB=6,AG==6.
∵CF⊥AD,AG⊥EB,∴∠EFC=∠G=90°,
又∵∠E为公共角,∴△EFC∽△EGA,
∴,∴EG=9,∴BE=EG-BG=9-6,
∴S四边形ABCD=S△ABE-S△CDE=BE·AG-6=(9-6)×6-6=75-18.
(3)AD=.
期末检测卷一
(120分钟 150分)
题号
一
二
三
四
五
六
七
八
总分
得分
一、选择题(本大题共10小题,每小题4分,满分40分)
题 号
1
2
3
4
5
6
7
8
9
10
答 案
1.若sin
(x-10)°=,则锐角x的度数是
A.20°
B.30°
C.40°
D.70°
2.反比例函数y=的图象分布在第二、四象限,则k的取值范围是
A.k<
B.k<
C.k>
D.k>
3.把二次函数y=x2-4x+3配方成y=a(x+h)2+m的形式,则h,m的值分别是
A.2,-1
B.-2,-1
C.-2,1
D.-1,-2
4.已知△ABC与△DEF相似,且面积的比为1∶4,则△ABC与△DEF对应中线的比为
A.1∶16
B.1∶4
C.1∶2
D.2∶1
5.若锐角α满足
A.0°<α<30°
B.30°<α<45°
C.45°<α<60°
D.0°<α<45°
6.如图,线段AB两个端点的坐标分别为A(2.5,5)和B(5,0).以原点为位似中心,将线段AB缩小得到线段CD.若点D的坐标为(2,0),则点C的坐标为
A.(1,2)
B.(1,2.5)
C.(1.25,2.5)
D.(1.5,3)
7.已知二次函数y=ax2+bx+c与一次函数y=mx+n(a,m≠0)的图象如图所示,则关于x的一元二次方程ax2+(b-m)x+c-n=0的根的情况是
A.有两个相等的实数根
B.有两个不相等的实数根
C.没有实数根
D.无法确定
8.如图,过△ABC的顶点C作CD⊥AB于点D,下列条件中不能判断△ABC是直角三角形的是
A.
B.AC2=AD·AB
C.BC2=BD·AB
D.CD2=AD·BD
9.某公司研制出一种新产品,该产品的成本为每件2400元.在试销期间,购买不超过10件时,每件销售价为3000元;购买超过10件时,每多购买一件,所购产品的销售单价均降低5元.设购买这种产品x件(其中x>10,且x为整数),该公司所获利润为y元,则y与x之间的函数表达式是
A.y=-5x2-650x
B.y=-5x2-3050x
C.y=-5x2+650x
D.y=-5x2+3050x
10.如图,在△ABC中,AB=AC=10,tan
A=2,BE⊥AC于点E,D是线段BE上的一个动点,则CD+BD的最小值是
A.2
B.10
C.5
D.4
二、填空题(本大题共4小题,每小题5分,满分20分)
11.若点(-2,3)在反比例函数y=的图象上,则k的值为 .?
12.如图,在5×5的正方形网格中,每个小正方形的边长都是1,△ABC是格点三角形(顶点是网格线的交点),则cos∠BAC的值为?
.?
13.已知点A(-1,y1)和点B(2,y2)都在抛物线y=x2-2x+c上,则y1 y2.(填“>”“=”或“<”)?
14.如图,在矩形ABCD
中,AB=3,点E在边BC
上,且BE∶CE
=2∶1
.连接AE
,将△ABE
沿AE
折叠,若点B的对应点B'落在矩形ABCD
的边上,则AD的长为?
.?
三、(本大题共2小题,每小题8分,满分16分)
15.已知≠0,且2x+3y-z=18,求4x+y-3z的值.
16.已知抛物线y=x2+x+c与x轴没有交点.
(1)求c的取值范围;
(2)试确定直线y=cx+1经过的象限.
四、(本大题共2小题,每小题8分,满分16分)
17.《九章算术》中有一道这样的题,原文如下:“今有邑,东西七里,南北九里,各中开门,出东门一十五里有木,问:出南门几何步而见木?”
大意为:今有一座长方形小城(如图),东西向城墙长7里,南北向城墙长9里,各城墙正中均开一城门,走出东门15里处有棵大树,问走出南门多少步恰好能望见这棵树?(注:1里=300步)
请解答上述问题.
18.如图,小方格是边长为1的正方形,△ABC是格点三角形(顶点在网格线的交点上).画格点△A'B'C',使△A'B'C'与△ABC相似但不全等,并说明理由.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,游客从离水平地面1400米高的A处坐缆车出发,沿俯角为60°的方向滑行1000米到达D处,再沿俯角为30°的方向滑行到山脚C处,求水平距离BC的长.(结果保留整数,参考数据:≈1.73)
20.我们规定:对于锐角α,β有下列三角函数关系,sin
(α±β)=sin
αcos
β±cos
αsin
β;cos
(α±β)=cos
αcos
β?sin
αsin
β.根据这个规定,解答下列问题:
(1)求sin
105°的值;
(2)求cos
15°的值.(结果保留根号)
六、(本题满分12分)
21.如图,已知直线y=ax+b与x轴交于点A(-2,0),与y轴交于点B(0,1),与反比例函数y=(x>0)交于点C(1,m).
(1)求m的值,并确定一次函数与反比例函数的表达式;
(2)经过点D且垂直于x轴的直线与直线y=ax+b交于点P,与反比例函数y=(x>0)的图象交于点Q.若AB∶AP=1∶3,求△APQ的面积.
七、(本题满分12分)
22.如图,直线y=kx+b(k,b为常数)分别与x轴、y轴交于点C(-3,0),D(0,3),抛物线y=-x2+x+2与x轴交于点A和点B(点A在点B的左侧).
(1)求直线y=kx+b的表达式;
(2)求点A和点B的坐标;
(3)若直线l与x轴垂直,在点A与点B之间移动,且与直线y=kx+b(k,b为常数)交于点E,与抛物线y=-x2+x+2交于点F,求EF的最小值.
八、(本题满分14分)
23.已知四边形ABCD的一组对边AD,BC的延长线相交于点E.
(1)如图1,若∠ABC=∠ADC=90°,求证:ED·EA=EC·EB;
(2)如图2,若∠ABC=120°,cos
∠ADC=,CD=5,AB=12,△CDE的面积为6,求四边形ABCD的面积;
(3)如图3,另一组对边AB,DC的延长线相交于点F.若cos∠ABC=cos∠ADC=,CD=5,CF=ED=n,直接写出AD的长.(用含n的式子表示)
参考答案
一、选择题(本大题共10小题,每小题4分,满分40分)
题 号
1
2
3
4
5
6
7
8
9
10
答 案
C
D
B
C
B
A
B
A
C
D
10.【提示】作DH⊥AB于点H,
CM⊥AB于点M.∴易得AE=2,BE=4.∵AB=AC,BE⊥AC,
CM⊥AB,∴
CM=BE=4(等腰三角形两腰上的高相等).易知DH=BD,∴CD+BD=CD+DH.∵CD+DH≥CM,∴CD+BD≥4,∴CD+BD的最小值为4.
二、填空题(本大题共4小题,每小题5分,满分20分)
11. -6
12.?
13. >
14.?
【提示】设BC=AD=x,∵BE∶CE
=2∶1,∴BE=x,CE=x.由折叠的性质得,AB=A
B'=3,
∠B'=∠B=90°,BE=
B'E=x.由题意可得,点B'的位置有两种情况:①当点B'落在矩形的边AD上时,则四边形ABEB'为正方形,∴B'E=AB=BE=3,则x=3,∴x=;②当点B'落在边CD上时,由已知可得BE=B'E=x,EC=x.易得△AB'D∽△B'EC,∴,∴DB'=AB'=.在Rt△ADB'中,由勾股定理可得AD=.综上所述,AD的长为.
三、(本大题共2小题,每小题8分,满分16分)
15.解:设=k,可得x=2k,y=3k,z=4k,
代入2x+3y-z=18中,得4k+9k-4k=18,解得k=2,
所以x=4,y=6,z=8,
所以4x+y-3z=16+6-24=-2.
16.解:(1)c>.
(2)直线y=cx+1经过第一、二、三象限.
四、(本大题共2小题,每小题8分,满分16分)
17.解:由题意,得AB=15里,AC=4.5里,CD=3.5里,
∵DE⊥CD,AC⊥CD,∴AC∥DE,∴△ACB∽△DEC,
∴,即,解得DE=1.05(里)=315步,
∴走出南门315步恰好能望见这棵树.
18.
解:如图所示.(本题答案不唯一)
理由:由勾股定理得AB=,AC=,BC=5,A'B'=,B'C'=,A'C'=2,∴,∴△ABC∽△A'B'C'.
五、(本大题共2小题,每小题10分,满分20分)
19.解:过点D作DE⊥AB于点E,DF⊥BC于点F.
由题意知∠DAE=30°,∴DE=AD=×1000=500,在Rt△ADE中,AE==500,
∴DF=AB-AE=1400-500.
在Rt△DFC中,CF=(1400-500)=1400-1500,∴BC=DE+CF=500+1400-1500=1400-1000≈1422(米).
20.解:(1)sin
105°=sin
(45°+60°)=sin
45°cos
60°+cos
45°sin
60°=.
(2)cos
15°=cos
(45°-30°)=cos
45°cos
30°+sin
45°sin
30°=.
六、(本题满分12分)
21.解:(1)∵直线y=ax+b经过点A(-2,0),点B(0,1),
∴解得∴一次函数的表达式为y=x+1.
∵点C(1,m)在直线y=x+1上,∴m=+1=.
∵点C在反比例函数y=(k>0)的图象上,
∴k=,∴反比例函数的表达式为y=.
(2)∵BO⊥AD,PD⊥AD,∴BO∥PD,∴.
∵AB∶AP=1∶3,AO=2,∴OD=2AO=4,∴点D的坐标为(4,0),
∴点P的坐标为(4,3),点Q的坐标为(4,).
∴△APQ的面积=.
七、(本题满分12分)
22.解:(1)易得直线的表达式是y=x+3.
(2)点A的坐标为(-1,0),点B的坐标为(3,0).
(3)令点E,F的横坐标为a,EF=s,则点F的纵坐标为-a2+a+2,点E的纵坐标为a+3,所以s=(a+3)-a2-a+1(-1
八、(本题满分14分)
23.解:(1)略.
(2)过点C作CF⊥AD于点F,过点A作AG⊥EB交EB的延长线于点G.
在Rt△CDF中,cos
∠ADC=,又∵CD=5,∴DF=3,∴CF==4.
∵S△CDE=6,
∴ED·CF=6,∴ED=3,∴EF=ED+DF=6.
∵∠ABC=120°,∠G=90°,∴∠BAG=30°.
在Rt△ABG中,BG=AB=6,AG==6.
∵CF⊥AD,AG⊥EB,∴∠EFC=∠G=90°,
又∵∠E为公共角,∴△EFC∽△EGA,
∴,∴EG=9,∴BE=EG-BG=9-6,
∴S四边形ABCD=S△ABE-S△CDE=BE·AG-6=(9-6)×6-6=75-18.
(3)AD=.
同课章节目录
