2020年秋沪科版九年级上册数学 期末检测卷二(Word版 含答案)
文档属性
| 名称 | 2020年秋沪科版九年级上册数学 期末检测卷二(Word版 含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 222.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-25 00:00:00 | ||
图片预览




文档简介
沪科版九年级上册数学检测卷
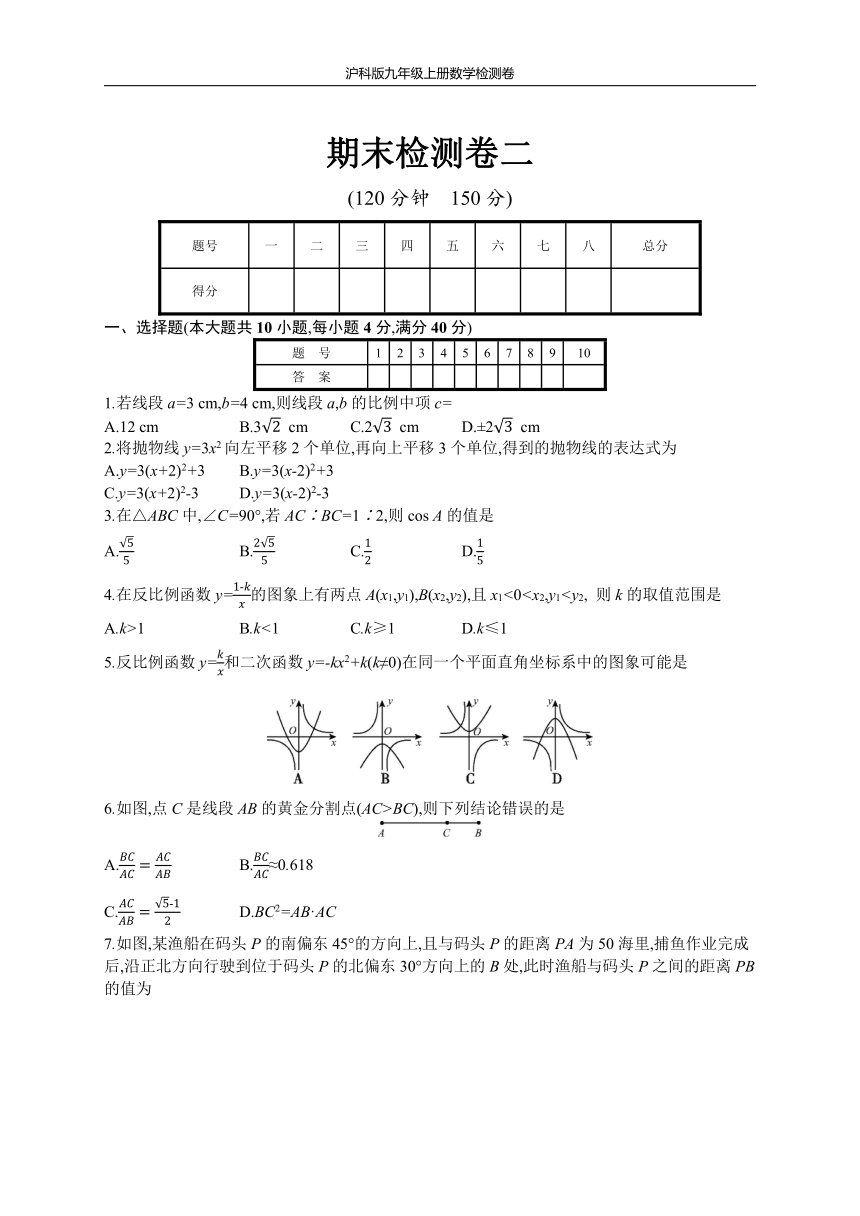
期末检测卷二
(120分钟 150分)
题号
一
二
三
四
五
六
七
八
总分
得分
一、选择题(本大题共10小题,每小题4分,满分40分)
题 号
1
2
3
4
5
6
7
8
9
10
答 案
1.若线段a=3
cm,b=4
cm,则线段a,b的比例中项c=
A.12
cm
B.3
cm
C.2
cm
D.±2
cm
2.将抛物线y=3x2向左平移2个单位,再向上平移3个单位,得到的抛物线的表达式为
A.y=3(x+2)2+3
B.y=3(x-2)2+3
C.y=3(x+2)2-3
D.y=3(x-2)2-3
3.在△ABC中,∠C=90°,若AC∶BC=1∶2,则cos
A的值是
A.
B.
C.
D.
4.在反比例函数y=的图象上有两点A(x1,y1),B(x2,y2),且x1<0则k的取值范围是
A.k>1
B.k<1
C.k≥1
D.k≤1
5.反比例函数y=和二次函数y=-kx2+k(k≠0)在同一个平面直角坐标系中的图象可能是
6.如图,点C是线段AB的黄金分割点(AC>BC),则下列结论错误的是
A.
B.≈0.618
C.
D.BC2=AB·AC
7.如图,某渔船在码头P的南偏东45°的方向上,且与码头P的距离PA为50海里,捕鱼作业完成后,沿正北方向行驶到位于码头P的北偏东30°方向上的B处,此时渔船与码头P之间的距离PB的值为
A.50
海里
B.100
海里
C.50
海里
D.100
海里
8.如图,在平行四边形ABCD中,AD=BD=5,AB=6,E为AB的中点,F为CD上一点,连接EF交BD于点G.若=2∶3,则EF的长是
A.
B.2
C.2
D.5
9.如图是二次函数y=ax2+bx+c(a≠0)的图象的一部分,已知它的对称轴是直线x=1,与x轴其中一个交点为(4,0).下列说法中:①abc<0;②2a+b=0;③a-b+c<0;④关于x的一元二次方程ax2+bx+c=0(a≠0)的解是x1=-2,x2=4.其中正确的说法有
A.①④
B.②③
C.①②④
D.①②③④
10.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,利用这个图形可求得tan
22.5°的值为
A.+1
B.-1
C.+1
D.-1
二、填空题(本大题共4小题,每小题5分,满分20分)
11.二次函数y=x2-2x-1的顶点坐标是
.?
12.如图,在平行四边形ABCD中,E是边AB的中点,连接DE交对角线AC于点F,则AF∶AC=
.?
13.如图,一次函数y=-x+b(a≠0)的图象与反比例函数y=(k≠0)的图象相交于点A(n-1,2m-6)和点B(9-m,5-2n).若OA=OB,则k的值为
.?
14.在平行四边形ABCD中,∠A=30°,AD=4,BD=4,则平行四边形ABCD的面积等于
.?
三、(本大题共2小题,每小题8分,满分16分)
15.计算:cos245°-2sin
60°-.
16.已知y=(2-a)x2-2(a-2)x+3是y关于x的二次函数.
(1)若该二次函数的图象开口向下,求a的取值范围.
(2)在(1)的条件下,求x满足什么条件时,y随x的增大而减小?
四、(本大题共2小题,每小题8分,满分16分)
17.【填空】(1)sin
30°=?
,cos
30°=?
,tan
30°=?
;?
(2)sin
45°=?
,cos
45°=?
,tan
45°=
;?
(3)sin
60°=?
,cos
60°=
,tan
60°=?
;?
【猜想】观察上述式子,猜想:若α是锐角,则sin
α,cos
α,tan
α之间的关系是
(不用说理);?
【应用】若sin
37°≈0.6,cos
37°≈0.8,则tan
37°≈
.?
18.如图,△ABC是格点三角形(顶点是网格线的交点),点O是格点.
(1)以点O为位似中心,作△ABC的位似图形△A1B1C1,使新图形与原图形的相似比为1∶2;
(2)若△ABC的面积是20
cm2,则△A1B1C1的面积为
.?
五、(本大题共2小题,每小题10分,满分20分)
19.我们知道叫作黄金数.阅读下列作图过程,解答后面的问题.
如图:(1)过点B作AB的垂线,并在垂线上取BC=AB;
(2)连接AC,以C为圆心,CB长为半径画弧,交AC于点E;
(3)以A为圆心,AE长为半径画弧,交AB于点P.
【说理】请运用所学知识说明点P是AB的黄金分割点;
【应用】已知BC=10
cm,M是BC的黄金分割点,求BM的长.
20.如图,一艘渔船从港口A沿北偏东60°方向AC航行,出发时测得灯塔D在港口A的北偏东30°方向上,当它航行10海里到达B点时,测得灯塔D在其正北方向上,当它继续航行到C港时,发现灯塔D在它的北偏西75°方向上(整个航行过程中航向始终保持不变).
(1)求出这次航行中离灯塔的最近距离;
(2)求C港与灯塔D之间的距离.
六、(本题满分12分)
21.为治理高速超速现象,确保行车安全.高速交警在距离高速路40米的地方设置了一个测速观察点A,现测得测速点的西北方向有一辆小型轿车从B处向正东方向行驶,2秒钟后到达测速点北偏东60°方向上的C处,如图.
(1)求该小型轿车在测速过程中的平均行驶速度约是多少千米/小时?(结果精确到1千米/小时,参考数据:≈1.4,≈1.7)
(2)我国交通法规定:小轿车在高速路行驶,时速超过限定时速10%以上不到50%的处200元罚款,扣3分;时速超过限定时速50%以上不到70%的处1500元罚款,扣12分;时速超过限定时速70%以上的处1500元罚款,扣12分.若该高速路段限速120千米/小时,你认为该小型轿车驾驶员会受到怎样的处罚?
七、(本题满分12分)
22.某商场经销一种成本价为20元/件的商品,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于成本价的1.8倍.在试销售过程中发现每天的销量y(件)与售价x(元/件)之间满足一次函数关系,对应关系如下表所示:
x(元/件)
20
24
28
32
36
y(件)
100
92
84
76
68
(1)求y与x之间的函数表达式,并写出自变量x的取值范围.
(2)该商场销售这种商品每天所获得的利润为w元,若每天销售这种商品需支付人员工资、管理费等各项费用共200元,求w与x之间的函数表达式,并求出这种商品的销售单价定为多少时,才能使商场每天获取的利润最大?最大利润是多少?
八、(本题满分14分)
23.在△ABC中,∠ACB=90°,BE是AC边上的中线,点D在射线BC上.小明进行了如下的探究:
探究1:如图1,点D在BC上,BD∶CD=3∶1,AD与BE相交于点P,求的值.
小明是这样解答的:“过点A作AF∥BC,交BE的延长线于点F,……”
请按照小明的思路,写出后面的说理过程.
探究2:如图2,点D在BC的延长线上,BC∶CD=3∶1,BE的延长线交AD于点P,求的值.
应用:在△ABC中,∠ACB=90°,AC=BC=4,BE是AC边上的中线,点D在射线BC上.请在探究1和探究2的条件下,分别求出BP的长.
参考答案
一、选择题(本大题共10小题,每小题4分,满分40分)
题 号
1
2
3
4
5
6
7
8
9
10
答 案
C
A
A
B
D
D
A
B
C
B
10.【提示】过点D作DE⊥AB于点E.令AC=BC=1,易证△CAD≌△EAD,∴AC=AE=1,易知AB=,BE=DE=DC=-1.在Rt△ACD中,tan
∠CAD=tan
22.5°=-1.
二、填空题(本大题共4小题,每小题5分,满分20分)
11. (1,-2)
12. 1∶3
13. 4
14.
16或8
三、(本大题共2小题,每小题8分,满分16分)
15.解:原式=-2×-[-(-2)]=-2=-.
16.解:(1)由题意,得2-a<0,解得a>2.
(2)该二次函数的对称轴是直线x=-=-1,由(1)得该二次函数的图象开口向下,∴当x>-1时,y随x的增大而减小.
四、(本大题共2小题,每小题8分,满分16分)
17.【填空】(1)? ? ?
(2)? ? 1
(3)? ? ?
【猜想】 tan
α=
【应用】 0.75
18.
解:(1)图略.
(2) 5
cm2
五、(本大题共2小题,每小题10分,满分20分)
19.解:【说理】设AB=a,由作法可知BC=CE=,根据勾股定理得AC=,所以AE=AP=a,所以P是AB的黄金分割点.
【应用】根据黄金分割点的概念,分两种情况:①当BM是较长线段时,BM=×10=(5-5)cm;②当BM是较短线段时,BM=10-(5-5)=(15-5)cm.
综上所述,BM的长是(5-5)cm或(15-5)cm.
20.解:(1)过D点作DE⊥AC于点E,则DE为最近距离.
在Rt△BDE中,∠DBE=60°,
∴BE=.
在Rt△ADE中,∠DAE=60°-30°=30°,
∴AE=DE.
又∵AE-BE=AB,即DE-=10,解得DE=5.
∴这次航行中离灯塔的最近距离为5
海里.
(2)在Rt△DEC中,∠ECD=180°-60°-75°=45°,
∴DC=DE=5(海里).
∴C港与灯塔D之间的距离为5
海里.
六、(本题满分12分)
21.解:(1)过点A作AD⊥BC于点D.
在Rt△ABD中,∵tan
45°=,
∴BD=40×1=40,
在Rt△ACD中,∵tan
60°=,
∴CD=40×≈68,
∴BC=BD+CD=108(米).
(108÷1000)÷(2÷3600)≈194(千米/小时).
答:该小型轿车在测速过程中的平均行驶速度约是194千米/小时.
(2)∵120×(1+10%)=132,120×(1+50%)=180,120×(1+70%)=204,而180<194<204,∴该小型轿车驾驶员会受到罚款1500元,扣12分的处罚.
七、(本题满分12分)
22.解:(1)y与x之间的函数表达式为y=-2x+140,自变量x的取值范围是20≤x≤36.
(2)由题意得w=(x-20)y-200=(x-20)(-2x+140)-200=-2x2+180x-3000=-2(x-45)2+1050,
∵-2<0,∴抛物线开口向下,当x<45时,w随x的增大而增大,又20≤x≤36,∴当x=36时,w取最大值,最大值为-2×(36-45)2+1050=888(元).
∴这种商品的销售单价定为36元/件时,才能使商场每天获取的利润最大,最大利润是888元.
八、(本题满分14分)
23.解:探究1:∵AF∥BC,∴∠AFE=∠CBE,∠FAE=∠BCE.∵AE=CE,∴△AFE≌△CBE,∴FE=BE,AF=BC.
∵BD∶CD=3∶1,∴AF∶BD=BC∶BD=4∶3.
∵AF∥BC,∴△AFP∽△DBP,∴.
探究2:过点A作AF∥BC,交BE的延长线于点F,∴∠AFE=∠CBE,∠FAE=∠BCE.∵AE=CE,∴△AFE≌△CBE,∴FE=BE,AF=CB.
∵BC∶CD=3∶1,∴AF∶BD=BC∶BD=3∶4.
∵AF∥BC,∴△AFP∽△DBP,∴.
应用:∵AC=BC=4,E是AC的中点,∴CE=2,根据勾股定理得BE==10,∴BF=20.
分两种情况:
(1)在探究1的条件下,∵AF∥BC,∴,∴BP=BF=×20=;
(2)在探究2的条件下,∵AF∥BC,∴,∴BP=BF=×20=.
综上所述,在探究1和探究2的条件下,BP的长分别为.
期末检测卷二
(120分钟 150分)
题号
一
二
三
四
五
六
七
八
总分
得分
一、选择题(本大题共10小题,每小题4分,满分40分)
题 号
1
2
3
4
5
6
7
8
9
10
答 案
1.若线段a=3
cm,b=4
cm,则线段a,b的比例中项c=
A.12
cm
B.3
cm
C.2
cm
D.±2
cm
2.将抛物线y=3x2向左平移2个单位,再向上平移3个单位,得到的抛物线的表达式为
A.y=3(x+2)2+3
B.y=3(x-2)2+3
C.y=3(x+2)2-3
D.y=3(x-2)2-3
3.在△ABC中,∠C=90°,若AC∶BC=1∶2,则cos
A的值是
A.
B.
C.
D.
4.在反比例函数y=的图象上有两点A(x1,y1),B(x2,y2),且x1<0
A.k>1
B.k<1
C.k≥1
D.k≤1
5.反比例函数y=和二次函数y=-kx2+k(k≠0)在同一个平面直角坐标系中的图象可能是
6.如图,点C是线段AB的黄金分割点(AC>BC),则下列结论错误的是
A.
B.≈0.618
C.
D.BC2=AB·AC
7.如图,某渔船在码头P的南偏东45°的方向上,且与码头P的距离PA为50海里,捕鱼作业完成后,沿正北方向行驶到位于码头P的北偏东30°方向上的B处,此时渔船与码头P之间的距离PB的值为
A.50
海里
B.100
海里
C.50
海里
D.100
海里
8.如图,在平行四边形ABCD中,AD=BD=5,AB=6,E为AB的中点,F为CD上一点,连接EF交BD于点G.若=2∶3,则EF的长是
A.
B.2
C.2
D.5
9.如图是二次函数y=ax2+bx+c(a≠0)的图象的一部分,已知它的对称轴是直线x=1,与x轴其中一个交点为(4,0).下列说法中:①abc<0;②2a+b=0;③a-b+c<0;④关于x的一元二次方程ax2+bx+c=0(a≠0)的解是x1=-2,x2=4.其中正确的说法有
A.①④
B.②③
C.①②④
D.①②③④
10.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,利用这个图形可求得tan
22.5°的值为
A.+1
B.-1
C.+1
D.-1
二、填空题(本大题共4小题,每小题5分,满分20分)
11.二次函数y=x2-2x-1的顶点坐标是
.?
12.如图,在平行四边形ABCD中,E是边AB的中点,连接DE交对角线AC于点F,则AF∶AC=
.?
13.如图,一次函数y=-x+b(a≠0)的图象与反比例函数y=(k≠0)的图象相交于点A(n-1,2m-6)和点B(9-m,5-2n).若OA=OB,则k的值为
.?
14.在平行四边形ABCD中,∠A=30°,AD=4,BD=4,则平行四边形ABCD的面积等于
.?
三、(本大题共2小题,每小题8分,满分16分)
15.计算:cos245°-2sin
60°-.
16.已知y=(2-a)x2-2(a-2)x+3是y关于x的二次函数.
(1)若该二次函数的图象开口向下,求a的取值范围.
(2)在(1)的条件下,求x满足什么条件时,y随x的增大而减小?
四、(本大题共2小题,每小题8分,满分16分)
17.【填空】(1)sin
30°=?
,cos
30°=?
,tan
30°=?
;?
(2)sin
45°=?
,cos
45°=?
,tan
45°=
;?
(3)sin
60°=?
,cos
60°=
,tan
60°=?
;?
【猜想】观察上述式子,猜想:若α是锐角,则sin
α,cos
α,tan
α之间的关系是
(不用说理);?
【应用】若sin
37°≈0.6,cos
37°≈0.8,则tan
37°≈
.?
18.如图,△ABC是格点三角形(顶点是网格线的交点),点O是格点.
(1)以点O为位似中心,作△ABC的位似图形△A1B1C1,使新图形与原图形的相似比为1∶2;
(2)若△ABC的面积是20
cm2,则△A1B1C1的面积为
.?
五、(本大题共2小题,每小题10分,满分20分)
19.我们知道叫作黄金数.阅读下列作图过程,解答后面的问题.
如图:(1)过点B作AB的垂线,并在垂线上取BC=AB;
(2)连接AC,以C为圆心,CB长为半径画弧,交AC于点E;
(3)以A为圆心,AE长为半径画弧,交AB于点P.
【说理】请运用所学知识说明点P是AB的黄金分割点;
【应用】已知BC=10
cm,M是BC的黄金分割点,求BM的长.
20.如图,一艘渔船从港口A沿北偏东60°方向AC航行,出发时测得灯塔D在港口A的北偏东30°方向上,当它航行10海里到达B点时,测得灯塔D在其正北方向上,当它继续航行到C港时,发现灯塔D在它的北偏西75°方向上(整个航行过程中航向始终保持不变).
(1)求出这次航行中离灯塔的最近距离;
(2)求C港与灯塔D之间的距离.
六、(本题满分12分)
21.为治理高速超速现象,确保行车安全.高速交警在距离高速路40米的地方设置了一个测速观察点A,现测得测速点的西北方向有一辆小型轿车从B处向正东方向行驶,2秒钟后到达测速点北偏东60°方向上的C处,如图.
(1)求该小型轿车在测速过程中的平均行驶速度约是多少千米/小时?(结果精确到1千米/小时,参考数据:≈1.4,≈1.7)
(2)我国交通法规定:小轿车在高速路行驶,时速超过限定时速10%以上不到50%的处200元罚款,扣3分;时速超过限定时速50%以上不到70%的处1500元罚款,扣12分;时速超过限定时速70%以上的处1500元罚款,扣12分.若该高速路段限速120千米/小时,你认为该小型轿车驾驶员会受到怎样的处罚?
七、(本题满分12分)
22.某商场经销一种成本价为20元/件的商品,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于成本价的1.8倍.在试销售过程中发现每天的销量y(件)与售价x(元/件)之间满足一次函数关系,对应关系如下表所示:
x(元/件)
20
24
28
32
36
y(件)
100
92
84
76
68
(1)求y与x之间的函数表达式,并写出自变量x的取值范围.
(2)该商场销售这种商品每天所获得的利润为w元,若每天销售这种商品需支付人员工资、管理费等各项费用共200元,求w与x之间的函数表达式,并求出这种商品的销售单价定为多少时,才能使商场每天获取的利润最大?最大利润是多少?
八、(本题满分14分)
23.在△ABC中,∠ACB=90°,BE是AC边上的中线,点D在射线BC上.小明进行了如下的探究:
探究1:如图1,点D在BC上,BD∶CD=3∶1,AD与BE相交于点P,求的值.
小明是这样解答的:“过点A作AF∥BC,交BE的延长线于点F,……”
请按照小明的思路,写出后面的说理过程.
探究2:如图2,点D在BC的延长线上,BC∶CD=3∶1,BE的延长线交AD于点P,求的值.
应用:在△ABC中,∠ACB=90°,AC=BC=4,BE是AC边上的中线,点D在射线BC上.请在探究1和探究2的条件下,分别求出BP的长.
参考答案
一、选择题(本大题共10小题,每小题4分,满分40分)
题 号
1
2
3
4
5
6
7
8
9
10
答 案
C
A
A
B
D
D
A
B
C
B
10.【提示】过点D作DE⊥AB于点E.令AC=BC=1,易证△CAD≌△EAD,∴AC=AE=1,易知AB=,BE=DE=DC=-1.在Rt△ACD中,tan
∠CAD=tan
22.5°=-1.
二、填空题(本大题共4小题,每小题5分,满分20分)
11. (1,-2)
12. 1∶3
13. 4
14.
16或8
三、(本大题共2小题,每小题8分,满分16分)
15.解:原式=-2×-[-(-2)]=-2=-.
16.解:(1)由题意,得2-a<0,解得a>2.
(2)该二次函数的对称轴是直线x=-=-1,由(1)得该二次函数的图象开口向下,∴当x>-1时,y随x的增大而减小.
四、(本大题共2小题,每小题8分,满分16分)
17.【填空】(1)? ? ?
(2)? ? 1
(3)? ? ?
【猜想】 tan
α=
【应用】 0.75
18.
解:(1)图略.
(2) 5
cm2
五、(本大题共2小题,每小题10分,满分20分)
19.解:【说理】设AB=a,由作法可知BC=CE=,根据勾股定理得AC=,所以AE=AP=a,所以P是AB的黄金分割点.
【应用】根据黄金分割点的概念,分两种情况:①当BM是较长线段时,BM=×10=(5-5)cm;②当BM是较短线段时,BM=10-(5-5)=(15-5)cm.
综上所述,BM的长是(5-5)cm或(15-5)cm.
20.解:(1)过D点作DE⊥AC于点E,则DE为最近距离.
在Rt△BDE中,∠DBE=60°,
∴BE=.
在Rt△ADE中,∠DAE=60°-30°=30°,
∴AE=DE.
又∵AE-BE=AB,即DE-=10,解得DE=5.
∴这次航行中离灯塔的最近距离为5
海里.
(2)在Rt△DEC中,∠ECD=180°-60°-75°=45°,
∴DC=DE=5(海里).
∴C港与灯塔D之间的距离为5
海里.
六、(本题满分12分)
21.解:(1)过点A作AD⊥BC于点D.
在Rt△ABD中,∵tan
45°=,
∴BD=40×1=40,
在Rt△ACD中,∵tan
60°=,
∴CD=40×≈68,
∴BC=BD+CD=108(米).
(108÷1000)÷(2÷3600)≈194(千米/小时).
答:该小型轿车在测速过程中的平均行驶速度约是194千米/小时.
(2)∵120×(1+10%)=132,120×(1+50%)=180,120×(1+70%)=204,而180<194<204,∴该小型轿车驾驶员会受到罚款1500元,扣12分的处罚.
七、(本题满分12分)
22.解:(1)y与x之间的函数表达式为y=-2x+140,自变量x的取值范围是20≤x≤36.
(2)由题意得w=(x-20)y-200=(x-20)(-2x+140)-200=-2x2+180x-3000=-2(x-45)2+1050,
∵-2<0,∴抛物线开口向下,当x<45时,w随x的增大而增大,又20≤x≤36,∴当x=36时,w取最大值,最大值为-2×(36-45)2+1050=888(元).
∴这种商品的销售单价定为36元/件时,才能使商场每天获取的利润最大,最大利润是888元.
八、(本题满分14分)
23.解:探究1:∵AF∥BC,∴∠AFE=∠CBE,∠FAE=∠BCE.∵AE=CE,∴△AFE≌△CBE,∴FE=BE,AF=BC.
∵BD∶CD=3∶1,∴AF∶BD=BC∶BD=4∶3.
∵AF∥BC,∴△AFP∽△DBP,∴.
探究2:过点A作AF∥BC,交BE的延长线于点F,∴∠AFE=∠CBE,∠FAE=∠BCE.∵AE=CE,∴△AFE≌△CBE,∴FE=BE,AF=CB.
∵BC∶CD=3∶1,∴AF∶BD=BC∶BD=3∶4.
∵AF∥BC,∴△AFP∽△DBP,∴.
应用:∵AC=BC=4,E是AC的中点,∴CE=2,根据勾股定理得BE==10,∴BF=20.
分两种情况:
(1)在探究1的条件下,∵AF∥BC,∴,∴BP=BF=×20=;
(2)在探究2的条件下,∵AF∥BC,∴,∴BP=BF=×20=.
综上所述,在探究1和探究2的条件下,BP的长分别为.
同课章节目录
