北师大版数学八年级上册 5.5 应用二元一次方程组——里程碑上的数课件(28张PPT)
文档属性
| 名称 | 北师大版数学八年级上册 5.5 应用二元一次方程组——里程碑上的数课件(28张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 725.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-25 13:10:27 | ||
图片预览








文档简介
第五章 二元一次方程组
5 应用二元一次方程组——里程碑上的数
名师导学
A. 应用二元一次方程组解决的常见实际问题还有:(1)数字问题:两位数=10×十位数字+个位数字;(2)行程问题:路程=速度×时间;
(3)工程问题:工作量=工作效率×时间;
(4)配套问题:总量各部分之间的比例=每一套各部分之间的比例;
(5)其他问题.
1. 根据题意列出二元一次方程组:
(1)有一个两位数,它的两个数字之和为11,把这个两位数的个位数字与十位数字对调,所得的新数比原数大63,设原两位数的个位数字为x,十位数字为y,根据题意可列方程组为
___________________________;
x+y=11,
10x+y-(10y+x)=63
{
(2)临沂至济南全长约338 km,一辆小汽车和一辆客车分别从临沂、济南两地同时相向开出,经过2 h相遇,相遇时,小汽车比客车多行驶32 km,设小汽车和客车的平均速度分别为x km/h和y km/h,则根
据题意可列方程组为_____________________.
课堂讲练
典型例题
新知1:数字问题
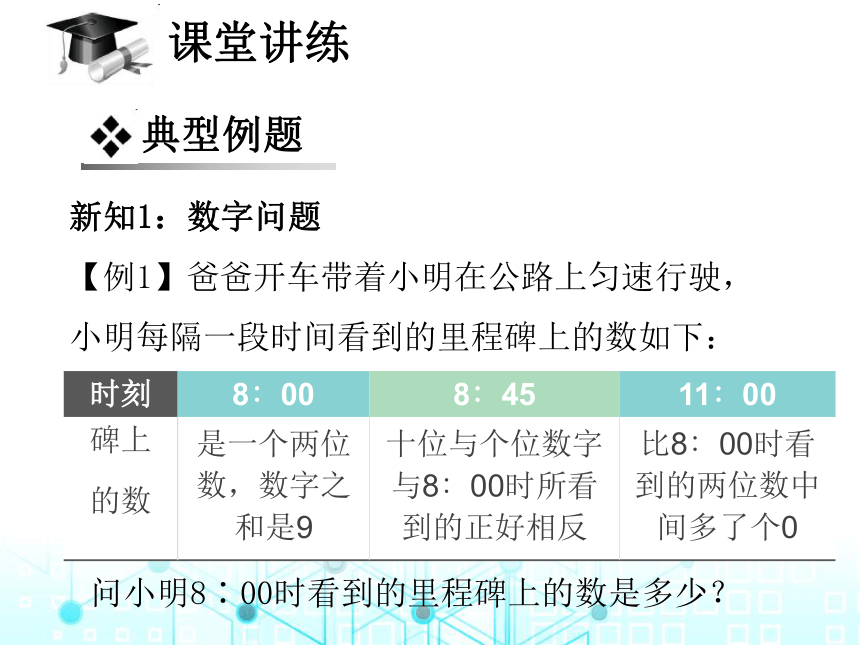
【例1】爸爸开车带着小明在公路上匀速行驶,小明每隔一段时间看到的里程碑上的数如下:
时刻
8∶00
8∶45
11∶00
碑上
的数
是一个两位数,数字之和是9
十位与个位数字与8∶00时所看到的正好相反
比8∶00时看到的两位数中间多了个0
问小明8∶00时看到的里程碑上的数是多少?
解:设小明8∶00看到的两位数,十位数
字为x,个位数字为y,即为10x+y;则8∶45时看到的两位数为x+10y,8∶00~8∶45时行驶的里程数为(10y+x)-(10x+y);则11∶00时看到的数为100x+y,8∶45~11∶00时行驶的里程数为
(100x+y)-(10y+x).由题意列方程组,得
解得 所以8∶00时看到的两位数是27.
答:8∶00时看到的里程碑上的两位数是27.
模拟演练
1. 有两个比40大的两位数,它们的差是20,大数的4倍与小数的和能被29整除,求这两个两位数.
解:设这两个两位数分别为x,y.
根据题意,得
解得
因为n为正整数,且两个两位数均大于40,
所以
答:这两个两位数分别为62,42或91,71.
典型例题
新知2:行程问题
【例2】从A地到B地全程290 km,前一路段为国道,其余路段为高速公路. 已知汽车在国道上行驶的速度为60 km/h,在高速公路上行驶的速度为100 km/h,一辆客车从A地开往B地一共行驶了3.5 h. 求A,B两地间国道和高速公路各多少千米.
解:设A,B两地间国道和高速公路分别是x km,y km.依题意,得
答:A,B两地间国道和高速公路分别是90 km和200 km.
模拟演练
2. 已知某江上游甲地到下游乙地相距360 km,一艘轮船往返于甲、乙两地之间. 此轮船现由甲地顺流而下到达乙地用18 h,由乙地逆流而上到达甲地用24 h. 求此轮船在静水中的速度以及此江水流的
速度.
解:设轮船在静水中的速度为x km/h,此江水流的速度为y km/h.根据题意,得
解得
答:此轮船在静水中的速度为17.5 km/h,此江水流的速度为2.5 km/h.
典型例题
新知3:其他问题
【例3】某工程队承包了一段全长1 957 m的隧道工程,甲、乙两个班组分别从南北两端同时掘进,已知甲组比乙组每天多掘进0.5 m,经过6天施工,甲、乙两组共掘进57 m,那么甲、乙两个班组平均每天各掘进多少米?
解:设甲班组平均每天掘进x m,乙班组平均每天掘进y m.根据题意,得
解得
答:甲班组平均每天掘进5 m,乙班组平均每天掘进4.5 m.
模拟演练
3. 某工厂车间生产甲、乙两种零部件. 已知1个甲零部件和2个乙零部件配套成一个完整产品,每个工人每天可生产14个甲零部件或20个乙零部件. 现有60名工人,则每天应安排多少个工人生产甲零部件,多少个工人生产乙零部件,才能使生产出来的两种零部件刚好配套?
解:设每天应安排x个工人生产甲零部件,y个工人生产乙零部件,才能使生产出来的两种零部件刚好配套.依题意,得
解得
答:每天应安排25个工人生产甲零部件,35个工人生产乙零部件,才能使生产出来的两种零部件刚好配套.
分层训练
【A组】
1. 一个两位数,十位上数字比个位上数字大2,且十位上数字与个位上数字之和为12,则这个两位数为 ( )
A. 46 B. 64 C. 57 D. 75
D
2. 小明的生日的月和日相加是36,月的2倍和日相加是44,则小明的生日是 ( )
A. 6月30日 B. 7月29日
C. 8月28日 D. 9月27日
C
3. 小明的爸爸骑着摩托车带着小明在公路上匀速行驶,小明每隔一段时间看到的里程碑上的数如下:12:00时是一个两位数,数字之和为7;13:00时十位数字与个位数字与12:00时所看到的正好互
换了;14:00时比12:00时看到的两位数中间多出一个0. 如果设小明在12:00时看到的数的十位数字是x,个位数字是y,根据题意可列方程组为
_______________________________________.
4. 如图5-5-1,10块相同的小长方形墙砖拼成一个大长方形,设小长方形墙砖的长和宽分别为
x cm和y cm,则可列方程组为
_______________.
【B组】
5. A,B两地相距36 km,甲从A地步行到B地,乙从B地步行到A地,两人同时相向出发,4 h后两人相遇;6 h后,甲剩余的路程是乙剩余路程的
2倍. 求两人的速度.
解:设甲、乙两人的速度分别为x km/h,y km/h.由题意,得
解得
答:甲、乙两人的速度分别为4 km/h和5 km/h.
6. 修建某一建筑时,若请甲、乙两个工程队同时施工,8天可以完成,需付两队费用共3520元;若先请甲队单独做6天,再请乙队单独做12天可以完成,需付两队费用共3 480元.问甲、乙两队每天费用各为多少?
解:设甲队每天费用为x元,乙队每天费用为y元,由题意,得
8x+8y=3 520,
6x+12y=3 480.
解得 x=300,
y=140.
答:甲队每天费用为300元,乙队每天费用为140元.
{
{
【C组】
7. 小明问李老师的年龄. 李老师回答:“当我的岁数是你现在的岁数时,你才1岁. ”小明想了想,说:“当我的岁数是你现在的岁数时,你已是40岁. ”听了他们的对话,你知道李老师和小明现在各是多少岁吗?
解:设现在李老师x岁,小明y岁.依题意,得
x-y=y-1,
40-x=x-y.
解得 x=27,
y=14.
答:现在李老师27岁,小明14岁.
{
{
8. 某个三位数是它各位数字和的27倍,已知百位数字与个位数字之和比十位数字大1,再把这个三位数的百位数字与个位数字交换位置,得到一个新的三位数,新的三位数比原来的三位数大99,求原来的三位数.
解:设原来的三位数的百位数字为x,个位数字为y,则十位数字为x+y-1.根据题意,得
100x+10(x+y-1)+y=27(x+y+x+y-1),
100y+10(x+y-1)+x=100x+10(x+y-1)+y+99.
化简,得 43y-56x=17,
y-x=1.
解得 x=2,
y=3.
所以x+y-1=4.
答:原来的三位数为243.
{
{
{
5 应用二元一次方程组——里程碑上的数
名师导学
A. 应用二元一次方程组解决的常见实际问题还有:(1)数字问题:两位数=10×十位数字+个位数字;(2)行程问题:路程=速度×时间;
(3)工程问题:工作量=工作效率×时间;
(4)配套问题:总量各部分之间的比例=每一套各部分之间的比例;
(5)其他问题.
1. 根据题意列出二元一次方程组:
(1)有一个两位数,它的两个数字之和为11,把这个两位数的个位数字与十位数字对调,所得的新数比原数大63,设原两位数的个位数字为x,十位数字为y,根据题意可列方程组为
___________________________;
x+y=11,
10x+y-(10y+x)=63
{
(2)临沂至济南全长约338 km,一辆小汽车和一辆客车分别从临沂、济南两地同时相向开出,经过2 h相遇,相遇时,小汽车比客车多行驶32 km,设小汽车和客车的平均速度分别为x km/h和y km/h,则根
据题意可列方程组为_____________________.
课堂讲练
典型例题
新知1:数字问题
【例1】爸爸开车带着小明在公路上匀速行驶,小明每隔一段时间看到的里程碑上的数如下:
时刻
8∶00
8∶45
11∶00
碑上
的数
是一个两位数,数字之和是9
十位与个位数字与8∶00时所看到的正好相反
比8∶00时看到的两位数中间多了个0
问小明8∶00时看到的里程碑上的数是多少?
解:设小明8∶00看到的两位数,十位数
字为x,个位数字为y,即为10x+y;则8∶45时看到的两位数为x+10y,8∶00~8∶45时行驶的里程数为(10y+x)-(10x+y);则11∶00时看到的数为100x+y,8∶45~11∶00时行驶的里程数为
(100x+y)-(10y+x).由题意列方程组,得
解得 所以8∶00时看到的两位数是27.
答:8∶00时看到的里程碑上的两位数是27.
模拟演练
1. 有两个比40大的两位数,它们的差是20,大数的4倍与小数的和能被29整除,求这两个两位数.
解:设这两个两位数分别为x,y.
根据题意,得
解得
因为n为正整数,且两个两位数均大于40,
所以
答:这两个两位数分别为62,42或91,71.
典型例题
新知2:行程问题
【例2】从A地到B地全程290 km,前一路段为国道,其余路段为高速公路. 已知汽车在国道上行驶的速度为60 km/h,在高速公路上行驶的速度为100 km/h,一辆客车从A地开往B地一共行驶了3.5 h. 求A,B两地间国道和高速公路各多少千米.
解:设A,B两地间国道和高速公路分别是x km,y km.依题意,得
答:A,B两地间国道和高速公路分别是90 km和200 km.
模拟演练
2. 已知某江上游甲地到下游乙地相距360 km,一艘轮船往返于甲、乙两地之间. 此轮船现由甲地顺流而下到达乙地用18 h,由乙地逆流而上到达甲地用24 h. 求此轮船在静水中的速度以及此江水流的
速度.
解:设轮船在静水中的速度为x km/h,此江水流的速度为y km/h.根据题意,得
解得
答:此轮船在静水中的速度为17.5 km/h,此江水流的速度为2.5 km/h.
典型例题
新知3:其他问题
【例3】某工程队承包了一段全长1 957 m的隧道工程,甲、乙两个班组分别从南北两端同时掘进,已知甲组比乙组每天多掘进0.5 m,经过6天施工,甲、乙两组共掘进57 m,那么甲、乙两个班组平均每天各掘进多少米?
解:设甲班组平均每天掘进x m,乙班组平均每天掘进y m.根据题意,得
解得
答:甲班组平均每天掘进5 m,乙班组平均每天掘进4.5 m.
模拟演练
3. 某工厂车间生产甲、乙两种零部件. 已知1个甲零部件和2个乙零部件配套成一个完整产品,每个工人每天可生产14个甲零部件或20个乙零部件. 现有60名工人,则每天应安排多少个工人生产甲零部件,多少个工人生产乙零部件,才能使生产出来的两种零部件刚好配套?
解:设每天应安排x个工人生产甲零部件,y个工人生产乙零部件,才能使生产出来的两种零部件刚好配套.依题意,得
解得
答:每天应安排25个工人生产甲零部件,35个工人生产乙零部件,才能使生产出来的两种零部件刚好配套.
分层训练
【A组】
1. 一个两位数,十位上数字比个位上数字大2,且十位上数字与个位上数字之和为12,则这个两位数为 ( )
A. 46 B. 64 C. 57 D. 75
D
2. 小明的生日的月和日相加是36,月的2倍和日相加是44,则小明的生日是 ( )
A. 6月30日 B. 7月29日
C. 8月28日 D. 9月27日
C
3. 小明的爸爸骑着摩托车带着小明在公路上匀速行驶,小明每隔一段时间看到的里程碑上的数如下:12:00时是一个两位数,数字之和为7;13:00时十位数字与个位数字与12:00时所看到的正好互
换了;14:00时比12:00时看到的两位数中间多出一个0. 如果设小明在12:00时看到的数的十位数字是x,个位数字是y,根据题意可列方程组为
_______________________________________.
4. 如图5-5-1,10块相同的小长方形墙砖拼成一个大长方形,设小长方形墙砖的长和宽分别为
x cm和y cm,则可列方程组为
_______________.
【B组】
5. A,B两地相距36 km,甲从A地步行到B地,乙从B地步行到A地,两人同时相向出发,4 h后两人相遇;6 h后,甲剩余的路程是乙剩余路程的
2倍. 求两人的速度.
解:设甲、乙两人的速度分别为x km/h,y km/h.由题意,得
解得
答:甲、乙两人的速度分别为4 km/h和5 km/h.
6. 修建某一建筑时,若请甲、乙两个工程队同时施工,8天可以完成,需付两队费用共3520元;若先请甲队单独做6天,再请乙队单独做12天可以完成,需付两队费用共3 480元.问甲、乙两队每天费用各为多少?
解:设甲队每天费用为x元,乙队每天费用为y元,由题意,得
8x+8y=3 520,
6x+12y=3 480.
解得 x=300,
y=140.
答:甲队每天费用为300元,乙队每天费用为140元.
{
{
【C组】
7. 小明问李老师的年龄. 李老师回答:“当我的岁数是你现在的岁数时,你才1岁. ”小明想了想,说:“当我的岁数是你现在的岁数时,你已是40岁. ”听了他们的对话,你知道李老师和小明现在各是多少岁吗?
解:设现在李老师x岁,小明y岁.依题意,得
x-y=y-1,
40-x=x-y.
解得 x=27,
y=14.
答:现在李老师27岁,小明14岁.
{
{
8. 某个三位数是它各位数字和的27倍,已知百位数字与个位数字之和比十位数字大1,再把这个三位数的百位数字与个位数字交换位置,得到一个新的三位数,新的三位数比原来的三位数大99,求原来的三位数.
解:设原来的三位数的百位数字为x,个位数字为y,则十位数字为x+y-1.根据题意,得
100x+10(x+y-1)+y=27(x+y+x+y-1),
100y+10(x+y-1)+x=100x+10(x+y-1)+y+99.
化简,得 43y-56x=17,
y-x=1.
解得 x=2,
y=3.
所以x+y-1=4.
答:原来的三位数为243.
{
{
{
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
