北师大版数学八年级上册 5.7 用二元一次方程组确定一次函数表达式课件(32张PPT)
文档属性
| 名称 | 北师大版数学八年级上册 5.7 用二元一次方程组确定一次函数表达式课件(32张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-25 13:10:04 | ||
图片预览









文档简介
第五章 二元一次方程组
7 用二元一次方程组确定一次函数表达式
名师导学
A. 先设出函数表达式,再根据所给条件确定表达式中_________________,从而得到函数表达式的方法,叫做待定系数法.
1. 一次函数y=kx+b,经过(1,1),(2,-4),则k与b的值为 ( )
未知的系数
C
课堂讲练
典型例题
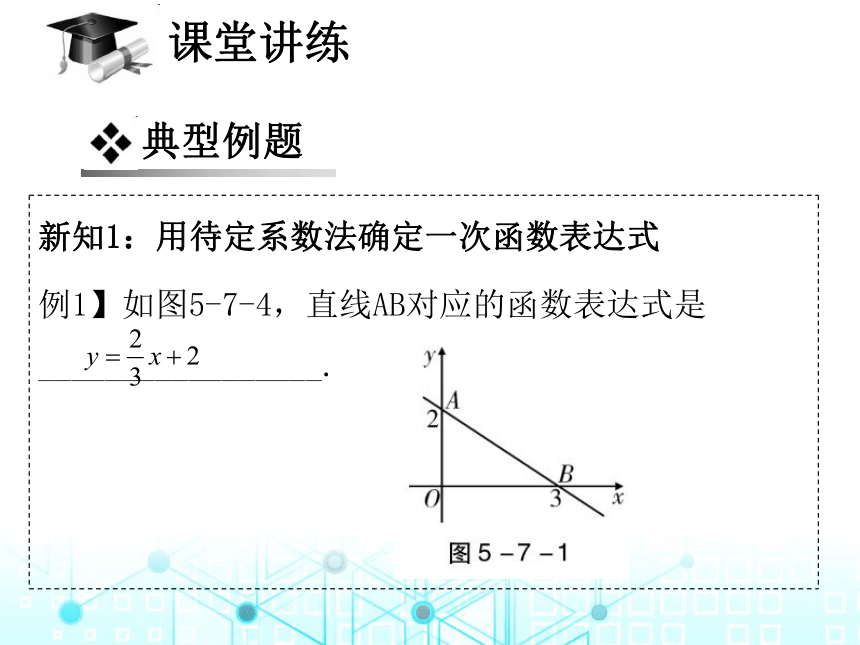
新知1:用待定系数法确定一次函数表达式
例1】如图5-7-4,直线AB对应的函数表达式是_________________.
模拟演练
1. 一次函数的图象经过点(2,1)和(-1,-3),则它的解析式为 ( )
D
典型例题
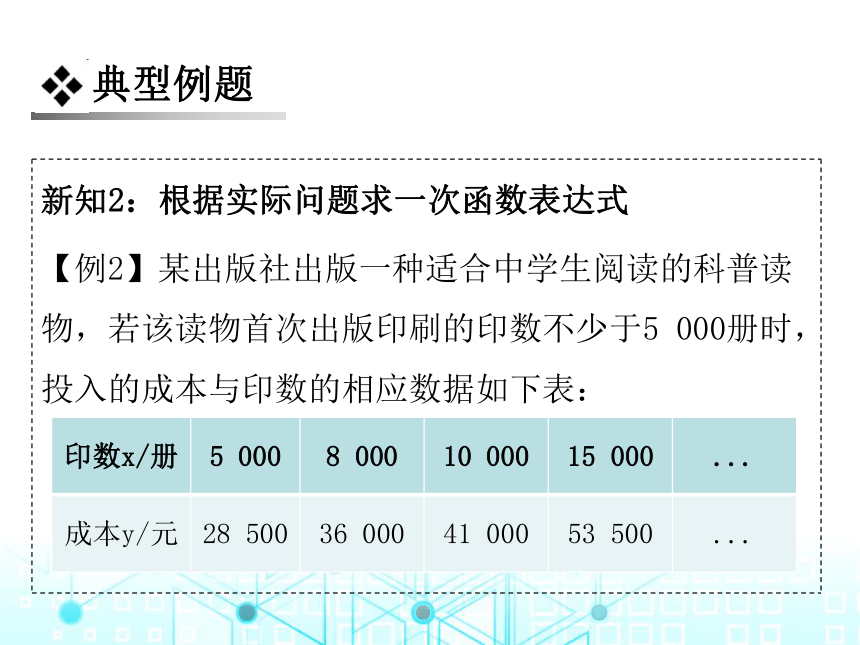
新知2:根据实际问题求一次函数表达式
【例2】某出版社出版一种适合中学生阅读的科普读物,若该读物首次出版印刷的印数不少于5 000册时,投入的成本与印数的相应数据如下表:
印数x/册
5 000
8 000
10 000
15 000
...
成本y/元
28 500
36 000
41 000
53 500
...
(1)经过对上表中数据的探究,发现这种读物的投入成本y(元)是印数x(册)的一次函数,求这个一次函数的解析式(不要求写出x的取值范围);
(2)如果出版社投入成本48 000元,那么能印该读物多少册?
解:(1)设所求一次函数的解析式为
y=kx+b(k≠0).由题意,
得 5 000k+b=28 500,
8 000k+b=36 000.
解得 k=52,
b=16 000.
所以这个一次函数的解析式为
y= x+16 000.
{
{
(2)将y=48 000代入y= x+16 000,
得48 000= x+16 000.解得x=12 800.答:能印该读物12 800册.
模拟演练
2. 某商场经营一批进价为2元的小商品,在市场营销中发现此商品的日销售单价x(元)与日销售量
y(件)之间有如下关系:
x/元
3
5
9
11
y/件
18
14
6
2
(1)求日销售量y与日销售单价x的函数关系式;
(2)根据(1)中所求的函数关系式计算当日销售单价为6元时,日销售量是多少件.
解:(1)设y与x的函数关系式为y=kx+b.
根据表中数据可得
所以y与x的函数关系式为y=-2x+24.
解得
(2)令x=6,则y=-2×6+24=12.
所以此时的日销售量为12件.
典型例题
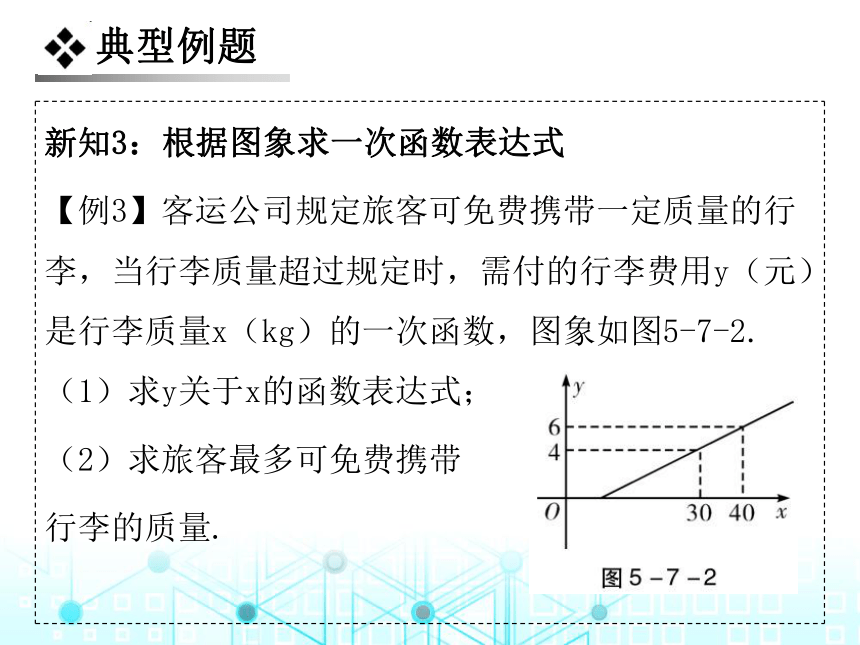
新知3:根据图象求一次函数表达式
【例3】客运公司规定旅客可免费携带一定质量的行李,当行李质量超过规定时,需付的行李费用y(元)是行李质量x(kg)的一次函数,图象如图5-7-2. (1)求y关于x的函数表达式;
(2)求旅客最多可免费携带
行李的质量.
解:(1)设y与x的函数表达式为y=kx+b,由图象得
解得
所以y与x的函数表达式为y= x-2.
(2)当y=0时, x-2=0,所以x=10. 所以旅客最多可免费携带行李的质量为10 kg.
3. 如图5-7-3,线段AB,CD分别是一辆轿车的油箱剩余油量y1(L)与一辆客车的油箱剩余油量y2(L)关于行驶路程x(km)的函数图象.
(1)分别求y1,y2关于x的函数解析式,并写出x的取值范围;
(2)如果两车同时出发,轿车的行驶速度为每小时100 km,客车的行驶速度为每小时80 km,当油箱的剩余油量相同时,两车行驶的时间相差多少分钟?
解:(1)根据图象,设AB,CD所表示的函数解析式分别为
结合图形可知
0=500k1+50,
0=400k2+80.
解得 k1=-0.1,
k2=-0.2.
所以 y1=-0.1x+50(0≤x≤500),
y2=-0.2x+80(0≤x≤400).
{
{
{
(2)令y1=y2,则有-0.1x+50=-0.2x+80.
解得x=300.
所以轿车行驶的时间为300÷100=3(h);
客车行驶的时间为300÷80= (h).
-3= (h)=45(min).
答:当油箱的剩余油量相同时,两车行驶的时间相差45 min.
分层训练
【A组】
1. 如图5-7-4,一次函数y=kx+b的图象经过点A,B,则它的解析式是 ( )
A. y=2x+3
B. y=-2x+3
C. y=- x+3
D. y=- x+3
C
2. 若点A(2,-3),B(4,3),C(5,a)在同一条直线上,则a的值是 ( )
A. 6或-6 B. 6
C. -6 D. 6或3
B
3. 生产某种产品所需的成本y(万元)与数量x(t)之间的关系如图5-7-5.
(1)y与x的函数关系式是__________;
(2)生产60 t这种产品,所需的成本为__________万元.
y= x+10
50
4. 如图5-7-6,矩形OABC的边OA在x轴上,O与原点重合,OA=1,OC=2,点D的坐标为(2,0),则直线BD的函数表达式为_________________.
y=-2x+4
【B组】
5. 儿童用药的剂量常常按他们的体重来计算. 某种药品,体重10 kg的儿童,每次正常服用量为110 mg;体重15 kg的儿童每次正常服用量为160 mg;体重在5~50 kg范围内时,每次正常服用量y(mg)是儿童体重x(kg)的一次函数. 求y与x之间的函数关系式,并写出自变量x的取值范围.
{
{
解:设y与x之间的函数关系式为y=kx+b(k≠0).依题意,得
10k+b=110,
15k+b=160.
解得 k=10,
b=10.
所以y与x之间的函数关系式为y=10x+10(5≤x≤50).
6. 某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作,已知该种水果的进价为8元/kg,下面是他们在活动结束后的对话.
小丽:如果以10元/kg的价格销售,那么每天可售出300 kg.
小强:如果以13元/kg的价格销售,那么每天可获取利润750元.
小红:通过调查验证,我发现每天的销售量y(kg)与销售单价x(元)之间存在一次函数关系.
求y(kg)与x(元)(x>0)之间的函数关系式.
解:由题意知当销售单价为13元/kg时,每天的销售数量为 =150(kg).
设y与x之间的一次函数关系式为y=kx+b,由题意,得
300=10k+b,
150=13k+b.
解得 k=-50,
b=800.
则y与x之间的函数关系式为y=-50x+800.
{
{
【C组】
7. 某网络公司推出了一系列上网包月业务,其中的一项业务是10M“40元包200 h”,且其中每月收取的费用y(元)与上网时间x(h)的函数关系如图5-7-7.
(1)当x≥200时,求y与x的函数关系式;
(2)若小明家10月份上网费
用为52元,则他家该月的
上网时间是多少小时?
解:(1)设当x≥200时,y与x的函数关系式为y=kx+b.
因为图象经过点(200,40),(220,70),
则有 40=200k+b,
70=220k+b.
解得 k= ,
b=-260.
所以y与x之间的函数关系式为y= x-260.
{
{
(2)把y=52代入y= -260,得x=208.
所以他家该月的上网时间是208 h.
8. 如图5-7-8表示两辆汽车的行驶路程s(km)与时间t(h)的关系(汽车B在汽车A后出发),试回答下列问题:
(1)图中l1,l2分别表示哪一辆汽车的路程与时间的关系?
(2)写出汽车A和汽车B的路程与时间的函数关系式,并写出汽车A和汽车B的速度各是多少;
(3)图中交点表示什么意思?
解:(1)因为汽车B在汽车A后出发,所以从图中可知l1表示汽车A的路程与时间的关系,l2表示汽车B的路程与时间的关系.
(2)汽车A的函数关系式是s= . 由题意,设汽车B的函数关系式即直线l2为s=kt+b,因为l2经过点(2,0)和(3,100),所以
0=2k+b,
100=3k+b. 解得 k=100,
b=-200.
所以汽车B的函数关系式是s=100t-200.
汽车A的速度是 km/h,
汽车B的速度是100 km/h.
{
{
(3)图中交点表示汽车A出发3 h(或汽车B出发1 h)后两车相遇,此时两车行驶路程都是100 km.
7 用二元一次方程组确定一次函数表达式
名师导学
A. 先设出函数表达式,再根据所给条件确定表达式中_________________,从而得到函数表达式的方法,叫做待定系数法.
1. 一次函数y=kx+b,经过(1,1),(2,-4),则k与b的值为 ( )
未知的系数
C
课堂讲练
典型例题
新知1:用待定系数法确定一次函数表达式
例1】如图5-7-4,直线AB对应的函数表达式是_________________.
模拟演练
1. 一次函数的图象经过点(2,1)和(-1,-3),则它的解析式为 ( )
D
典型例题
新知2:根据实际问题求一次函数表达式
【例2】某出版社出版一种适合中学生阅读的科普读物,若该读物首次出版印刷的印数不少于5 000册时,投入的成本与印数的相应数据如下表:
印数x/册
5 000
8 000
10 000
15 000
...
成本y/元
28 500
36 000
41 000
53 500
...
(1)经过对上表中数据的探究,发现这种读物的投入成本y(元)是印数x(册)的一次函数,求这个一次函数的解析式(不要求写出x的取值范围);
(2)如果出版社投入成本48 000元,那么能印该读物多少册?
解:(1)设所求一次函数的解析式为
y=kx+b(k≠0).由题意,
得 5 000k+b=28 500,
8 000k+b=36 000.
解得 k=52,
b=16 000.
所以这个一次函数的解析式为
y= x+16 000.
{
{
(2)将y=48 000代入y= x+16 000,
得48 000= x+16 000.解得x=12 800.答:能印该读物12 800册.
模拟演练
2. 某商场经营一批进价为2元的小商品,在市场营销中发现此商品的日销售单价x(元)与日销售量
y(件)之间有如下关系:
x/元
3
5
9
11
y/件
18
14
6
2
(1)求日销售量y与日销售单价x的函数关系式;
(2)根据(1)中所求的函数关系式计算当日销售单价为6元时,日销售量是多少件.
解:(1)设y与x的函数关系式为y=kx+b.
根据表中数据可得
所以y与x的函数关系式为y=-2x+24.
解得
(2)令x=6,则y=-2×6+24=12.
所以此时的日销售量为12件.
典型例题
新知3:根据图象求一次函数表达式
【例3】客运公司规定旅客可免费携带一定质量的行李,当行李质量超过规定时,需付的行李费用y(元)是行李质量x(kg)的一次函数,图象如图5-7-2. (1)求y关于x的函数表达式;
(2)求旅客最多可免费携带
行李的质量.
解:(1)设y与x的函数表达式为y=kx+b,由图象得
解得
所以y与x的函数表达式为y= x-2.
(2)当y=0时, x-2=0,所以x=10. 所以旅客最多可免费携带行李的质量为10 kg.
3. 如图5-7-3,线段AB,CD分别是一辆轿车的油箱剩余油量y1(L)与一辆客车的油箱剩余油量y2(L)关于行驶路程x(km)的函数图象.
(1)分别求y1,y2关于x的函数解析式,并写出x的取值范围;
(2)如果两车同时出发,轿车的行驶速度为每小时100 km,客车的行驶速度为每小时80 km,当油箱的剩余油量相同时,两车行驶的时间相差多少分钟?
解:(1)根据图象,设AB,CD所表示的函数解析式分别为
结合图形可知
0=500k1+50,
0=400k2+80.
解得 k1=-0.1,
k2=-0.2.
所以 y1=-0.1x+50(0≤x≤500),
y2=-0.2x+80(0≤x≤400).
{
{
{
(2)令y1=y2,则有-0.1x+50=-0.2x+80.
解得x=300.
所以轿车行驶的时间为300÷100=3(h);
客车行驶的时间为300÷80= (h).
-3= (h)=45(min).
答:当油箱的剩余油量相同时,两车行驶的时间相差45 min.
分层训练
【A组】
1. 如图5-7-4,一次函数y=kx+b的图象经过点A,B,则它的解析式是 ( )
A. y=2x+3
B. y=-2x+3
C. y=- x+3
D. y=- x+3
C
2. 若点A(2,-3),B(4,3),C(5,a)在同一条直线上,则a的值是 ( )
A. 6或-6 B. 6
C. -6 D. 6或3
B
3. 生产某种产品所需的成本y(万元)与数量x(t)之间的关系如图5-7-5.
(1)y与x的函数关系式是__________;
(2)生产60 t这种产品,所需的成本为__________万元.
y= x+10
50
4. 如图5-7-6,矩形OABC的边OA在x轴上,O与原点重合,OA=1,OC=2,点D的坐标为(2,0),则直线BD的函数表达式为_________________.
y=-2x+4
【B组】
5. 儿童用药的剂量常常按他们的体重来计算. 某种药品,体重10 kg的儿童,每次正常服用量为110 mg;体重15 kg的儿童每次正常服用量为160 mg;体重在5~50 kg范围内时,每次正常服用量y(mg)是儿童体重x(kg)的一次函数. 求y与x之间的函数关系式,并写出自变量x的取值范围.
{
{
解:设y与x之间的函数关系式为y=kx+b(k≠0).依题意,得
10k+b=110,
15k+b=160.
解得 k=10,
b=10.
所以y与x之间的函数关系式为y=10x+10(5≤x≤50).
6. 某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作,已知该种水果的进价为8元/kg,下面是他们在活动结束后的对话.
小丽:如果以10元/kg的价格销售,那么每天可售出300 kg.
小强:如果以13元/kg的价格销售,那么每天可获取利润750元.
小红:通过调查验证,我发现每天的销售量y(kg)与销售单价x(元)之间存在一次函数关系.
求y(kg)与x(元)(x>0)之间的函数关系式.
解:由题意知当销售单价为13元/kg时,每天的销售数量为 =150(kg).
设y与x之间的一次函数关系式为y=kx+b,由题意,得
300=10k+b,
150=13k+b.
解得 k=-50,
b=800.
则y与x之间的函数关系式为y=-50x+800.
{
{
【C组】
7. 某网络公司推出了一系列上网包月业务,其中的一项业务是10M“40元包200 h”,且其中每月收取的费用y(元)与上网时间x(h)的函数关系如图5-7-7.
(1)当x≥200时,求y与x的函数关系式;
(2)若小明家10月份上网费
用为52元,则他家该月的
上网时间是多少小时?
解:(1)设当x≥200时,y与x的函数关系式为y=kx+b.
因为图象经过点(200,40),(220,70),
则有 40=200k+b,
70=220k+b.
解得 k= ,
b=-260.
所以y与x之间的函数关系式为y= x-260.
{
{
(2)把y=52代入y= -260,得x=208.
所以他家该月的上网时间是208 h.
8. 如图5-7-8表示两辆汽车的行驶路程s(km)与时间t(h)的关系(汽车B在汽车A后出发),试回答下列问题:
(1)图中l1,l2分别表示哪一辆汽车的路程与时间的关系?
(2)写出汽车A和汽车B的路程与时间的函数关系式,并写出汽车A和汽车B的速度各是多少;
(3)图中交点表示什么意思?
解:(1)因为汽车B在汽车A后出发,所以从图中可知l1表示汽车A的路程与时间的关系,l2表示汽车B的路程与时间的关系.
(2)汽车A的函数关系式是s= . 由题意,设汽车B的函数关系式即直线l2为s=kt+b,因为l2经过点(2,0)和(3,100),所以
0=2k+b,
100=3k+b. 解得 k=100,
b=-200.
所以汽车B的函数关系式是s=100t-200.
汽车A的速度是 km/h,
汽车B的速度是100 km/h.
{
{
(3)图中交点表示汽车A出发3 h(或汽车B出发1 h)后两车相遇,此时两车行驶路程都是100 km.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
