北师大版数学八年级上册 5.4 应用二元一次方程组——增收节支 课件(30张PPT)
文档属性
| 名称 | 北师大版数学八年级上册 5.4 应用二元一次方程组——增收节支 课件(30张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 764.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-25 00:00:00 | ||
图片预览








文档简介
第五章 二元一次方程组
4 应用二元一次方程组——增收节支
名师导学
A. 应用二元一次方程组解决实际问题,可以利用__________的方式分析题中的已知量与未知量的关系.
列表
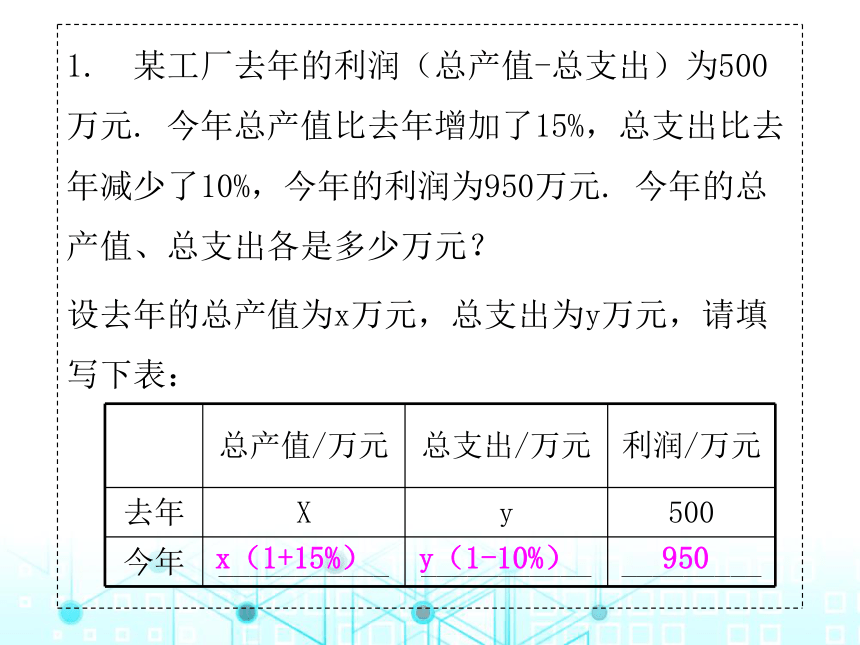
1. 某工厂去年的利润(总产值-总支出)为500万元. 今年总产值比去年增加了15%,总支出比去年减少了10%,今年的利润为950万元. 今年的总产值、总支出各是多少万元?
设去年的总产值为x万元,总支出为y万元,请填写下表:
总产值/万元
总支出/万元
利润/万元
去年
X
y
500
今年
___________
___________
_________
x(1+15%)
y(1-10%)
950
B. 应用二元一次方程组解决的常见实际问题有:(1)百分比问题;
(2)和差倍分问题;
(3)销售问题:利润=售价-进价(成本价)=利润率×进价(成本价).
2. 根据题意列出二元一次方程组:
某班有学生50人,其中男生比女生的2倍少7人. 如果设该班男生有x人,女生有y人,那么可列
方程组为______________________.
x+y=50,
x=2y-7
{
课堂讲练
典型例题
新知1:百分比问题
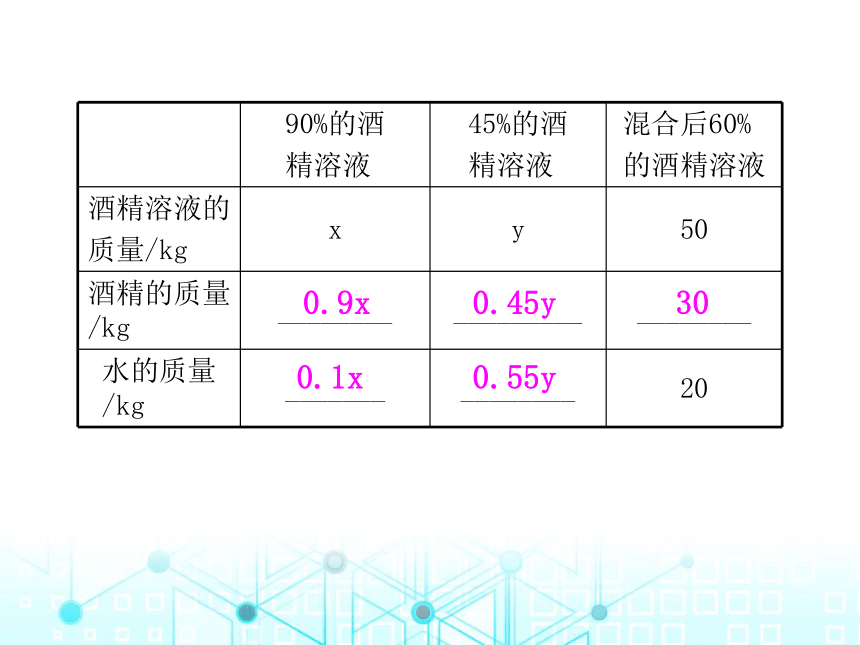
【例1】用质量分数为90%和45%的酒精溶液配制成质量分数为60%的酒精溶液,共50 kg. 设90%和45%的酒精溶液分别为x kg,y kg,填写下表并求x,y的值.
90%的酒
精溶液
45%的酒
精溶液
混合后60%
的酒精溶液
酒精溶液的
质量/kg
x
y
50
酒精的质量/kg
________
_________
________
水的质量/kg
_______
________
20
0.9x
0.45y
30
0.1x
0.55y
解:由题意,得
解得
答:质量分数为90%的酒精溶液质量为 kg,质量分数为45%的酒精溶液质量为 kg.
0.9x+0.45y=30,
0.1x+0.55y=20.
{
x= ,
y= .
{
模拟演练
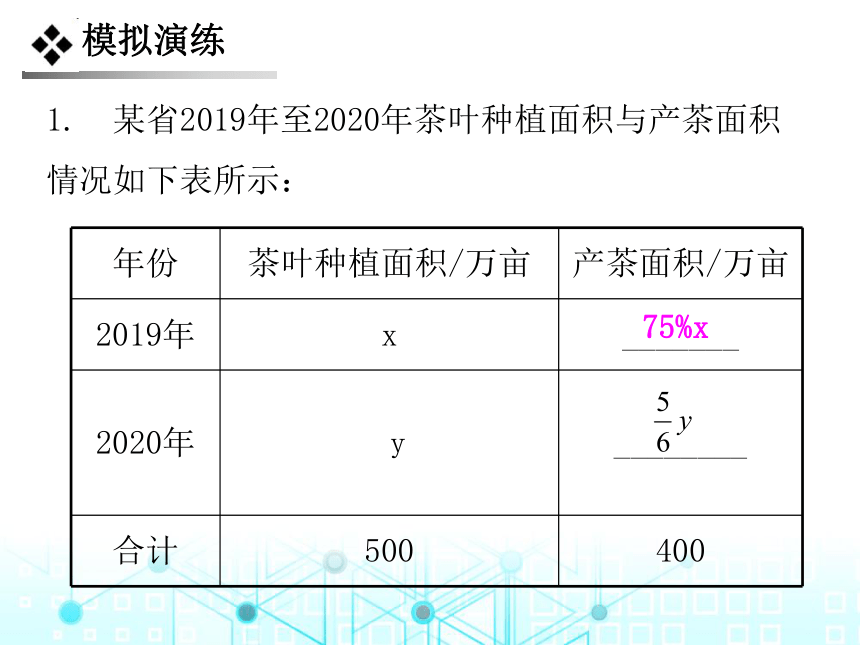
1. 某省2019年至2020年茶叶种植面积与产茶面积情况如下表所示:
年份
茶叶种植面积/万亩
产茶面积/万亩
2019年
x
_______
2020年
y
________
合计
500
400
75%x
其中2019年产茶面积占当年种植面积的75%,2020年产茶面积占当年种植面积的 .
请根据上面提供的信息,解答下列问题:
(1)用含x,y的式子填表;
(2)求2020年的产茶面积.
解:(2)根据题意,得
解得
则2020年的产茶面积为 ×300=250(万亩).
答:2020年的产茶面积为250万亩.
x+y=500,
75%x+ =400.
{
x=200,
y=300.
{
新知2:和差倍分问题
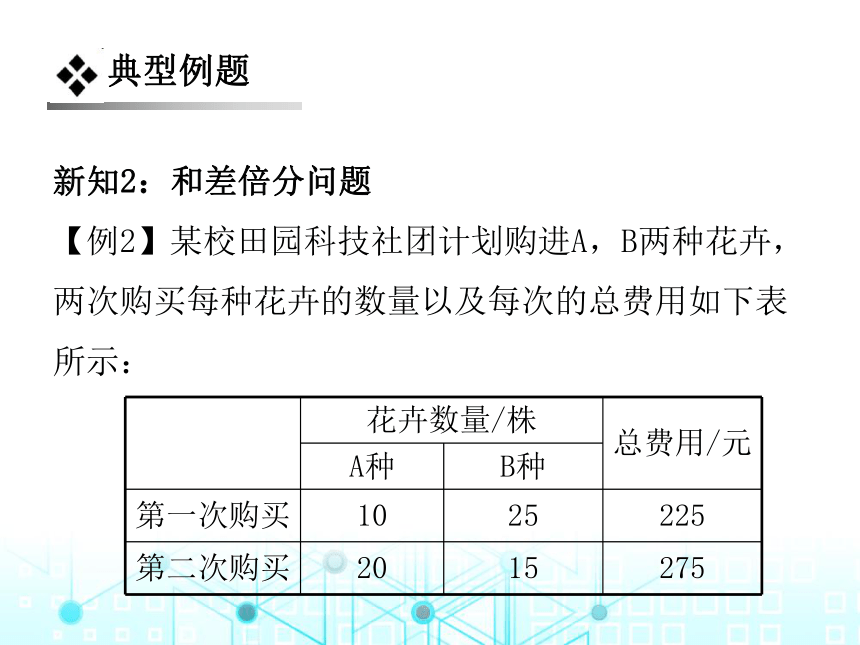
【例2】某校田园科技社团计划购进A,B两种花卉,两次购买每种花卉的数量以及每次的总费用如下表所示:
花卉数量/株
总费用/元
A种
B种
第一次购买
10
25
225
第二次购买
20
15
275
典型例题
则A,B两种花卉每株的价格各是多少元?
解:设A种花卉每株x元,B种花卉每株y元.
由题意,得
解得
答:A种花卉每株10元,B种花卉每株5元.
10x+25y=225,
20x+15y=275.
{
x=10,
y=5.
{
模拟演练
2. 某校订购了A,B两种笔记本,A种笔记本的单价为28元,B种笔记本的单价为24元. 若B种笔记本的订购数量比A种笔记本的2倍少20个,并且订购两种笔记本共用了2 560元,则该校分别订购了A,B两种笔记本多少个?
解:设该校订购了A种笔记本x个,B种笔记本y个.根据题意,得
答:该校订购了A种笔记本40个,B种笔记本60个.
y=2x-20,
28x+24y=2 560.
{
x=40,
y=60.
{
解得
典型例题
新知3:销售问题
【例3】甲、乙两件服装的成本共500元,商店老板为获取利润,决定将甲服装按55%的利润定价,乙服装按45%的利润定价. 在实际出售时,应顾客要求,两件服装均按八折出售,这样商店共获利104元. 甲、乙两件服装的成本各是多少元?
解:设甲服装的成本是x元,乙服装的成本是y元.
根据题意,得
答:甲服装的成本是300元,乙服装的成本是200元.
x+y=500,
x(1+55%)×0.8+y(1+45%)×0.8-x-y=104.
{
x=300,
y=200.
解得
{
模拟演练
3. 某商店购进一批衬衫,甲顾客以7折的优惠价格买了20件,乙顾客以8折的优惠价格买了5件,结果商店都获得利润200元,求这批衬衫的进价和标价各是多少元.
解:设这批衬衫的进价为x元,标价为y元.依题意,得
(0.7y-x)×20=200,
(0.8y-x)×5=200.
x=200,
y=300.
答:这批衬衫的进价为200元,标价为300元.
{
{
解得
分层训练
【A组】
1. 为了绿化校园,甲、乙两班共植树苗30棵,已知甲班植树数量是乙班的1.5倍,设甲班植树x棵,乙班植树y棵,根据题意,所列方程组正确的是 ( )
B
{
A.
x+y=30,
x=2.5y
{
A.
x+y=30,
x=1.5y
{
C.
x=y+30,
3y=2x
{
D.
x=y+30,
x=y+1.5
2. 某公司用30 000元购进两种货物,货物卖出后,一种货物的利润率是10%,另一种货物的利润率是11%,共获得利润3 150元. 设该两种货物的进价分别为x元,y元,根据题意列出方程组为
_____________________________.
x+y=30 000,
10%x+11%y=3 150
{
3. 甲、乙两种商品原来的单价和为100元,因市场变化,甲商品降价20%,乙商品提价60%,调整后两种商品的单价和比原来的单价和提高了50%,则购买调价后的3件甲商品和2件乙商品共需
__________元.
310
【B组】
4. 某地对居民家庭用电实行“阶梯电价”.电力公司规定:居民家庭每月用电量在80千瓦时以下(含80千瓦时,1千瓦时俗称1度)时,实行“基本电价”;当居民家庭月用电量超过80千瓦时时,超过部分实行“提高电价”. 小张家4月份用电100千瓦时,上缴电费68元;5月份用电120千瓦时,上缴电费88元. 求“基本电价”和“提高电价”分别为多少元/千瓦时.
解:设“基本电价”为x 元/千瓦时,“提高电价”为y元/千瓦时.根据题意,得
答:“基本电价”为0.6元/千瓦时,“提高电价”为1元/千瓦时.
80x+(100-80)y=68,
80x+(120-80)y=88.
{
x=0.6,
y=1.
{
解得
5. 为了提高农田利用效益,某地由每年种植双季稻改为先养殖小龙虾再种植一季水稻的“虾·稻”轮作模式. 某农户去年开始实施“虾·稻”轮作,去年出售小龙虾每千克获得的利润为32元. 由于开发成本下降和市场供求关系变化,现在每千克小龙虾的养殖成本下降25%,售价下降10%,出售小龙虾每千克获得的利润为30元. 求去年每千克小龙虾的养殖成本与售价.
解:设去年每千克小龙虾的养殖成本为x元,售价为y元.依题意,得
解得
答:去年每千克小龙虾的养殖成本为8元,售价为40元.
y-x=32,
(1-10%)y-(1-25%)x=30.
{
x=8,
y=40.
{
6. 某中学某班购买了35张电影票,共花250元,其中甲种票每张8元,乙种票每张6元,则甲、乙两种票各买了多少张?
设甲、乙两种票分别买了x张、y张,填写下表并求x,y的值.
甲
乙
总和
票数
x
y
______
钱数
______
______
______
35
8x
6y
250
解:根据题意,得
解得
答:甲种票买了20张,乙种票买了15张.
x+y=35,
8x+6y=250.
{
x=20,
y=15.
{
【C组】
7. 为了保护环境,某公交公司决定购买A,B两种型号的全新混合动力公交车共10辆,其中A种型号每辆价格为a万元,每年节省油量为2.4万升;B种型号每辆价格为b万元,每年节省油量为2.2万升. 经调查,购买一辆A型车比购买一辆B型车多20万元,购买2辆A型车比购买3辆B型车少60万元.
(1)请求出a和b的值;
(2)若购买这批混合动力公交车每年能节省22.4万升汽油,求购买这批混合动力公交车共需要多少万元.
a-b=20,
3b-2a=60.
解:(1)根据题意,得
解得
{
a=120,
b=100.
{
(2)设购买A型车x台,购买B型车y台.根据题意,得
解得
120×2+100×8=1 040(万元).
答:购买这批混合动力公交车共需要1 040万元.
x+y=10,
2.4x+2.2y=22.4.
{
x=2,
y=8.
{
4 应用二元一次方程组——增收节支
名师导学
A. 应用二元一次方程组解决实际问题,可以利用__________的方式分析题中的已知量与未知量的关系.
列表
1. 某工厂去年的利润(总产值-总支出)为500万元. 今年总产值比去年增加了15%,总支出比去年减少了10%,今年的利润为950万元. 今年的总产值、总支出各是多少万元?
设去年的总产值为x万元,总支出为y万元,请填写下表:
总产值/万元
总支出/万元
利润/万元
去年
X
y
500
今年
___________
___________
_________
x(1+15%)
y(1-10%)
950
B. 应用二元一次方程组解决的常见实际问题有:(1)百分比问题;
(2)和差倍分问题;
(3)销售问题:利润=售价-进价(成本价)=利润率×进价(成本价).
2. 根据题意列出二元一次方程组:
某班有学生50人,其中男生比女生的2倍少7人. 如果设该班男生有x人,女生有y人,那么可列
方程组为______________________.
x+y=50,
x=2y-7
{
课堂讲练
典型例题
新知1:百分比问题
【例1】用质量分数为90%和45%的酒精溶液配制成质量分数为60%的酒精溶液,共50 kg. 设90%和45%的酒精溶液分别为x kg,y kg,填写下表并求x,y的值.
90%的酒
精溶液
45%的酒
精溶液
混合后60%
的酒精溶液
酒精溶液的
质量/kg
x
y
50
酒精的质量/kg
________
_________
________
水的质量/kg
_______
________
20
0.9x
0.45y
30
0.1x
0.55y
解:由题意,得
解得
答:质量分数为90%的酒精溶液质量为 kg,质量分数为45%的酒精溶液质量为 kg.
0.9x+0.45y=30,
0.1x+0.55y=20.
{
x= ,
y= .
{
模拟演练
1. 某省2019年至2020年茶叶种植面积与产茶面积情况如下表所示:
年份
茶叶种植面积/万亩
产茶面积/万亩
2019年
x
_______
2020年
y
________
合计
500
400
75%x
其中2019年产茶面积占当年种植面积的75%,2020年产茶面积占当年种植面积的 .
请根据上面提供的信息,解答下列问题:
(1)用含x,y的式子填表;
(2)求2020年的产茶面积.
解:(2)根据题意,得
解得
则2020年的产茶面积为 ×300=250(万亩).
答:2020年的产茶面积为250万亩.
x+y=500,
75%x+ =400.
{
x=200,
y=300.
{
新知2:和差倍分问题
【例2】某校田园科技社团计划购进A,B两种花卉,两次购买每种花卉的数量以及每次的总费用如下表所示:
花卉数量/株
总费用/元
A种
B种
第一次购买
10
25
225
第二次购买
20
15
275
典型例题
则A,B两种花卉每株的价格各是多少元?
解:设A种花卉每株x元,B种花卉每株y元.
由题意,得
解得
答:A种花卉每株10元,B种花卉每株5元.
10x+25y=225,
20x+15y=275.
{
x=10,
y=5.
{
模拟演练
2. 某校订购了A,B两种笔记本,A种笔记本的单价为28元,B种笔记本的单价为24元. 若B种笔记本的订购数量比A种笔记本的2倍少20个,并且订购两种笔记本共用了2 560元,则该校分别订购了A,B两种笔记本多少个?
解:设该校订购了A种笔记本x个,B种笔记本y个.根据题意,得
答:该校订购了A种笔记本40个,B种笔记本60个.
y=2x-20,
28x+24y=2 560.
{
x=40,
y=60.
{
解得
典型例题
新知3:销售问题
【例3】甲、乙两件服装的成本共500元,商店老板为获取利润,决定将甲服装按55%的利润定价,乙服装按45%的利润定价. 在实际出售时,应顾客要求,两件服装均按八折出售,这样商店共获利104元. 甲、乙两件服装的成本各是多少元?
解:设甲服装的成本是x元,乙服装的成本是y元.
根据题意,得
答:甲服装的成本是300元,乙服装的成本是200元.
x+y=500,
x(1+55%)×0.8+y(1+45%)×0.8-x-y=104.
{
x=300,
y=200.
解得
{
模拟演练
3. 某商店购进一批衬衫,甲顾客以7折的优惠价格买了20件,乙顾客以8折的优惠价格买了5件,结果商店都获得利润200元,求这批衬衫的进价和标价各是多少元.
解:设这批衬衫的进价为x元,标价为y元.依题意,得
(0.7y-x)×20=200,
(0.8y-x)×5=200.
x=200,
y=300.
答:这批衬衫的进价为200元,标价为300元.
{
{
解得
分层训练
【A组】
1. 为了绿化校园,甲、乙两班共植树苗30棵,已知甲班植树数量是乙班的1.5倍,设甲班植树x棵,乙班植树y棵,根据题意,所列方程组正确的是 ( )
B
{
A.
x+y=30,
x=2.5y
{
A.
x+y=30,
x=1.5y
{
C.
x=y+30,
3y=2x
{
D.
x=y+30,
x=y+1.5
2. 某公司用30 000元购进两种货物,货物卖出后,一种货物的利润率是10%,另一种货物的利润率是11%,共获得利润3 150元. 设该两种货物的进价分别为x元,y元,根据题意列出方程组为
_____________________________.
x+y=30 000,
10%x+11%y=3 150
{
3. 甲、乙两种商品原来的单价和为100元,因市场变化,甲商品降价20%,乙商品提价60%,调整后两种商品的单价和比原来的单价和提高了50%,则购买调价后的3件甲商品和2件乙商品共需
__________元.
310
【B组】
4. 某地对居民家庭用电实行“阶梯电价”.电力公司规定:居民家庭每月用电量在80千瓦时以下(含80千瓦时,1千瓦时俗称1度)时,实行“基本电价”;当居民家庭月用电量超过80千瓦时时,超过部分实行“提高电价”. 小张家4月份用电100千瓦时,上缴电费68元;5月份用电120千瓦时,上缴电费88元. 求“基本电价”和“提高电价”分别为多少元/千瓦时.
解:设“基本电价”为x 元/千瓦时,“提高电价”为y元/千瓦时.根据题意,得
答:“基本电价”为0.6元/千瓦时,“提高电价”为1元/千瓦时.
80x+(100-80)y=68,
80x+(120-80)y=88.
{
x=0.6,
y=1.
{
解得
5. 为了提高农田利用效益,某地由每年种植双季稻改为先养殖小龙虾再种植一季水稻的“虾·稻”轮作模式. 某农户去年开始实施“虾·稻”轮作,去年出售小龙虾每千克获得的利润为32元. 由于开发成本下降和市场供求关系变化,现在每千克小龙虾的养殖成本下降25%,售价下降10%,出售小龙虾每千克获得的利润为30元. 求去年每千克小龙虾的养殖成本与售价.
解:设去年每千克小龙虾的养殖成本为x元,售价为y元.依题意,得
解得
答:去年每千克小龙虾的养殖成本为8元,售价为40元.
y-x=32,
(1-10%)y-(1-25%)x=30.
{
x=8,
y=40.
{
6. 某中学某班购买了35张电影票,共花250元,其中甲种票每张8元,乙种票每张6元,则甲、乙两种票各买了多少张?
设甲、乙两种票分别买了x张、y张,填写下表并求x,y的值.
甲
乙
总和
票数
x
y
______
钱数
______
______
______
35
8x
6y
250
解:根据题意,得
解得
答:甲种票买了20张,乙种票买了15张.
x+y=35,
8x+6y=250.
{
x=20,
y=15.
{
【C组】
7. 为了保护环境,某公交公司决定购买A,B两种型号的全新混合动力公交车共10辆,其中A种型号每辆价格为a万元,每年节省油量为2.4万升;B种型号每辆价格为b万元,每年节省油量为2.2万升. 经调查,购买一辆A型车比购买一辆B型车多20万元,购买2辆A型车比购买3辆B型车少60万元.
(1)请求出a和b的值;
(2)若购买这批混合动力公交车每年能节省22.4万升汽油,求购买这批混合动力公交车共需要多少万元.
a-b=20,
3b-2a=60.
解:(1)根据题意,得
解得
{
a=120,
b=100.
{
(2)设购买A型车x台,购买B型车y台.根据题意,得
解得
120×2+100×8=1 040(万元).
答:购买这批混合动力公交车共需要1 040万元.
x+y=10,
2.4x+2.2y=22.4.
{
x=2,
y=8.
{
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
