人教版数学七年级上册4.3.3 余角和补角练习课件(共31张PPT)
文档属性
| 名称 | 人教版数学七年级上册4.3.3 余角和补角练习课件(共31张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-26 15:46:38 | ||
图片预览










文档简介
4.3.3 余角和补角
1.掌握余角和补角的定义和性质,并能熟练应用.
2.正确地根据方位角确定方向.
1.互余和互补的概念:
余角:如果两个角的和等于___________,就说这两个角互为
余角(简称互余),其中一个角是另一个角的_____.
补角:如果两个角的和等于____________,就说这两个角互
为补角(简称互补),其中一个角是另一个角的_____.
90°(直角)
余角
180°(平角)
补角
2.余角和补角的性质:
如图,∠1与∠2互补,∠3与∠4互补,且∠1=∠3,∠2与∠4
有什么关系?
因为∠1与∠2互补,∠3与∠4互补,
所以∠1+∠2=______,∠3+∠4=______,
所以∠2=__________,∠4=__________,
又因为∠1=∠3,所以____=____.
180°
180°
180°-∠1
180°-∠3
∠2
∠4
【归纳】补角的性质:同角(等角)的补角_____.
余角的性质:同角(等角)的余角_____.
相等
相等
3.方位角:
方位角是以_____、_____方向为基准,描述物体运动方向的角.
正北
正南
(打“√”或“×”)
(1)互余的两角一定相等.( )
(2)两个小于90°的角一定互余.( )
(3)若∠1<90°,则∠1的补角大于90°( )
(4)相等且互补的两个角分别等于90°.( )
(5)东南方向在东和南之间的任意一条射线上.( )
×
×
√
√
×
知识点 1 余角和补角
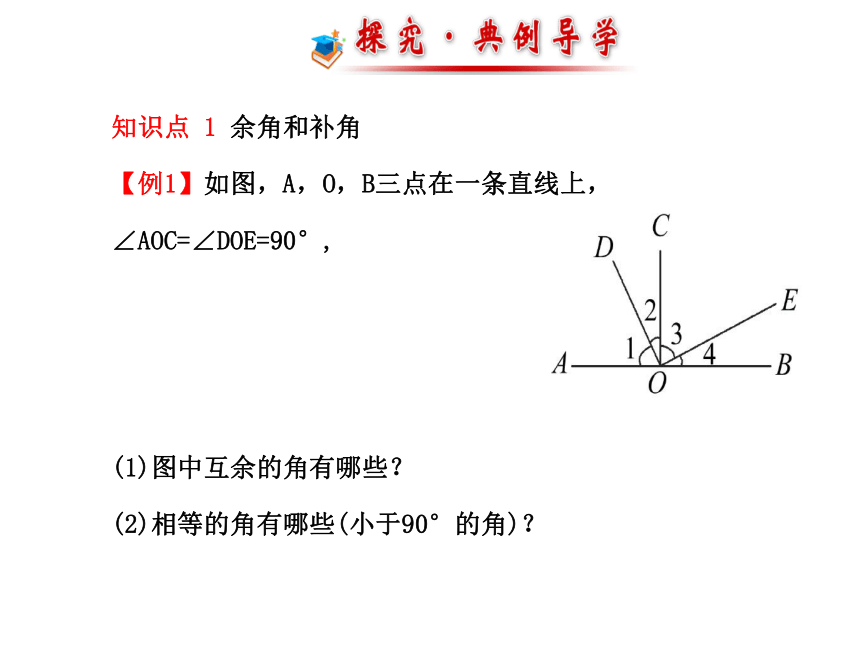
【例1】如图,A,O,B三点在一条直线上,∠AOC=∠DOE=90°,
(1)图中互余的角有哪些?
(2)相等的角有哪些(小于90°的角)?
【思路点拨】(1)找出图中所有90°的角→找出两角之和等于90°的角→答案
(2)利用余角的性质找相等的角
【自主解答】(1)因为∠AOC=∠DOE=90°,所以∠1+∠2=90°,∠3+∠2=90°,∠1+∠4=180°-∠DOE=90°.
又因为∠COB=180°-∠AOC=180°-90°=90°,
所以∠3+∠4=90°.
所以∠1与∠2互余、∠3与∠2互余、∠1与∠4互余、∠3与∠4互余.
(2)由同角的余角相等可得:∠1=∠3,∠2=∠4.
【总结提升】正确理解互余、互补
1.共同点:互余、互补都是反映两个角的数量关系,与角的位置无关,单独的一个角既不能互余也不能互补.
2.不同点:互余的两角之和等于90°,其中任何一角都小于90°;互补的两角之和等于180°,其中的两角不可能都小于90°,也不可能都大于90°.
知识点 2 方位角
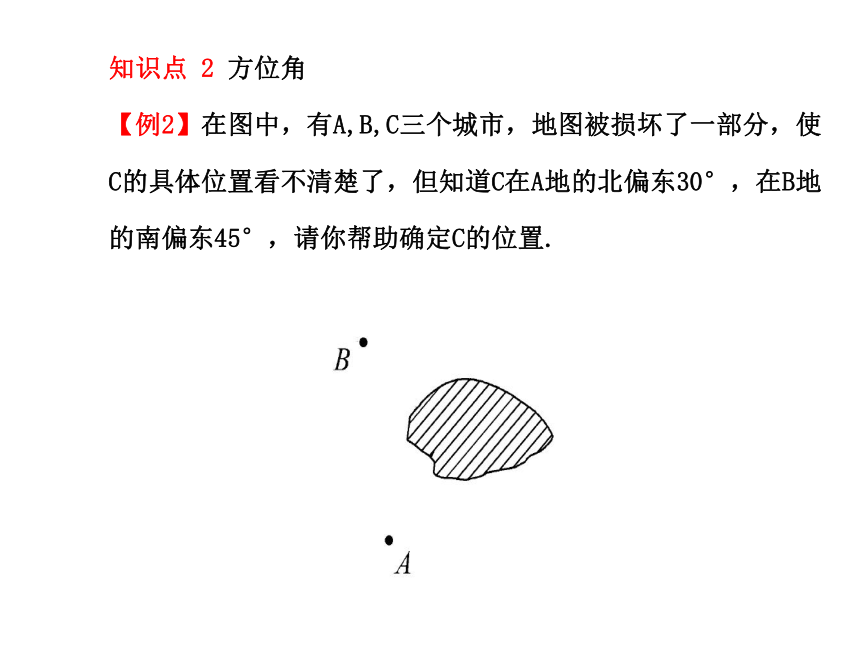
【例2】在图中,有A,B,C三个城市,地图被损坏了一部分,使C的具体位置看不清楚了,但知道C在A地的北偏东30°,在B地的南偏东45°,请你帮助确定C的位置.
【解题探究】1.C在A的北偏东30°是绕点A以什么方向为基准,沿什么方向旋转30°.
提示:以正北方向为基准,沿顺时针方向旋转30°.
2.C在B南偏东45°是绕点B以什么方向为基准,沿什么方向旋转45°.
提示:以正南方向为基准,沿逆时针方向旋转45°.
3.点C与以上两个方向线有什么关系?
提示:以上两个方向线的交点就是点C.如图:
【总结提升】应用方位角注意的几点
1.画方位角时,一般以正北或正南方向作角的始边.
2.一定要分清东、南、西、北.
3.书写方位角时,先写北或南,再写偏东或偏西,如“北偏东”不要写成“东偏北”.
4.“东北”方向指正北与正东方向的角平分线,“西北”“东南”“西南”依此类推.
题组一:余角和补角
1.(2012·长沙中考)下列四个角中,最有可能与70°角互补的是( )
【解析】选D.因为互补的两角之和是180°,所以70°角的补角应大于90°,故选D.
2.下列图形中,∠1和∠2互为余角的是( )
【解析】选D.选项A中的两角和的度数不能确定,选项B中∠1和∠2互补,选项C中∠1和∠2相等,选项D中∠1和∠2互余.
3.(2011·广州中考)已知∠α=26°,则∠α的补角是____度.
【解析】因为∠α=26°,所以∠α的补角是180°-26°=154°.
答案:154
【变式备选】一个角是35°39′,则它的余角为_______,补角为_______.
【解析】90°-35°39′=54°21′,
180°-35°39′=144°21′.
答案:54°21′ 144°21′
4.∠A与∠B互补,∠B与∠C互补,∠C=80°,则∠A的度数是________.
【解析】因为同角的补角相等,所以∠A=∠C=80°.
答案:80°
5.如图,O是直线AB上的点,OC是∠AOB的平分线,OD是一条射线,
∠AOD的补角是 ,余角是_______.
【解析】因为OC是∠AOB的平分线,
所以∠AOC=∠BOC=90°,
则∠AOD的补角是∠BOD,余角是∠COD.
答案:∠BOD ∠COD
6.∠A的余角和它的补角之比是1∶3,求∠A的度数.
【解析】设∠A的度数为x°,则180-x=3(90-x),
解得x=45.所以∠A的度数是45°.
题组二:方位角
1.在点O北偏西60°的某处有一点A,在点O南偏西20°的某处有一点B,则∠AOB的度数是( )
A.100° B.70° C.180° D.140°
【解析】选A.如图,∠AOB=180°-20°-60°=100°.
2.从A看B的方向是北偏东21°,那么从B看A的方向是( )
A.南偏东69° B.南偏西69°
C.南偏东21° D.南偏西21°
【解析】选D.如图,可知A点在B点的南偏西21°.
3.如图,点A,B在点O的方向分别是________.
【解析】由图可知点A在点O的北偏东30°,点B在点O的南偏东15°.
答案:北偏东30°,南偏东15°
4.画出射线OA,使射线OA在北偏西45°的方向上.
【解析】如图所示.
5.如图,一只蚂蚁从O点出发,沿东北方向爬行2.5 cm碰到障碍物B后,折向北偏西60°的方向爬行3 cm到C.
(1)画出蚂蚁的爬行路线.
(2)求出∠OBC的度数.
【解析】(1)先以O为顶点,表示正北方向的射线为角的一边,画45°的角,使它的一边OB′落在东与北之间,在射线OB′上取OB等于2.5 cm,同理以B点为顶点,画出BC=3 cm,则OB,BC是蚂蚁所爬行的路线.
如图所示:
(2)由题意知,点O在点B的西南方向,
所以∠DBO=45°,
因为∠CBE=60°,所以∠CBD=30°,
所以∠OBC=∠CBD+∠DBO
=30°+45°=75°.
【想一想错在哪?】如图,O是直线AB
上一点,OC为任意一条射线,OD平分
∠BOC,OE平分∠AOC.
(1)指出图中∠AOD与∠BOE的补角.
(2)试说明∠COD与∠COE具有怎样的数量关系.
提示:(1)本题找补角不全,互补的两个角与位置没有关系,不能只考虑图形中和是平角的两个角互补,还应该考虑和是180°的两个角也互补.(2)补角的性质是等角的补角相等,应用的条件是要考虑已知的两个角是不是相等.
1.掌握余角和补角的定义和性质,并能熟练应用.
2.正确地根据方位角确定方向.
1.互余和互补的概念:
余角:如果两个角的和等于___________,就说这两个角互为
余角(简称互余),其中一个角是另一个角的_____.
补角:如果两个角的和等于____________,就说这两个角互
为补角(简称互补),其中一个角是另一个角的_____.
90°(直角)
余角
180°(平角)
补角
2.余角和补角的性质:
如图,∠1与∠2互补,∠3与∠4互补,且∠1=∠3,∠2与∠4
有什么关系?
因为∠1与∠2互补,∠3与∠4互补,
所以∠1+∠2=______,∠3+∠4=______,
所以∠2=__________,∠4=__________,
又因为∠1=∠3,所以____=____.
180°
180°
180°-∠1
180°-∠3
∠2
∠4
【归纳】补角的性质:同角(等角)的补角_____.
余角的性质:同角(等角)的余角_____.
相等
相等
3.方位角:
方位角是以_____、_____方向为基准,描述物体运动方向的角.
正北
正南
(打“√”或“×”)
(1)互余的两角一定相等.( )
(2)两个小于90°的角一定互余.( )
(3)若∠1<90°,则∠1的补角大于90°( )
(4)相等且互补的两个角分别等于90°.( )
(5)东南方向在东和南之间的任意一条射线上.( )
×
×
√
√
×
知识点 1 余角和补角
【例1】如图,A,O,B三点在一条直线上,∠AOC=∠DOE=90°,
(1)图中互余的角有哪些?
(2)相等的角有哪些(小于90°的角)?
【思路点拨】(1)找出图中所有90°的角→找出两角之和等于90°的角→答案
(2)利用余角的性质找相等的角
【自主解答】(1)因为∠AOC=∠DOE=90°,所以∠1+∠2=90°,∠3+∠2=90°,∠1+∠4=180°-∠DOE=90°.
又因为∠COB=180°-∠AOC=180°-90°=90°,
所以∠3+∠4=90°.
所以∠1与∠2互余、∠3与∠2互余、∠1与∠4互余、∠3与∠4互余.
(2)由同角的余角相等可得:∠1=∠3,∠2=∠4.
【总结提升】正确理解互余、互补
1.共同点:互余、互补都是反映两个角的数量关系,与角的位置无关,单独的一个角既不能互余也不能互补.
2.不同点:互余的两角之和等于90°,其中任何一角都小于90°;互补的两角之和等于180°,其中的两角不可能都小于90°,也不可能都大于90°.
知识点 2 方位角
【例2】在图中,有A,B,C三个城市,地图被损坏了一部分,使C的具体位置看不清楚了,但知道C在A地的北偏东30°,在B地的南偏东45°,请你帮助确定C的位置.
【解题探究】1.C在A的北偏东30°是绕点A以什么方向为基准,沿什么方向旋转30°.
提示:以正北方向为基准,沿顺时针方向旋转30°.
2.C在B南偏东45°是绕点B以什么方向为基准,沿什么方向旋转45°.
提示:以正南方向为基准,沿逆时针方向旋转45°.
3.点C与以上两个方向线有什么关系?
提示:以上两个方向线的交点就是点C.如图:
【总结提升】应用方位角注意的几点
1.画方位角时,一般以正北或正南方向作角的始边.
2.一定要分清东、南、西、北.
3.书写方位角时,先写北或南,再写偏东或偏西,如“北偏东”不要写成“东偏北”.
4.“东北”方向指正北与正东方向的角平分线,“西北”“东南”“西南”依此类推.
题组一:余角和补角
1.(2012·长沙中考)下列四个角中,最有可能与70°角互补的是( )
【解析】选D.因为互补的两角之和是180°,所以70°角的补角应大于90°,故选D.
2.下列图形中,∠1和∠2互为余角的是( )
【解析】选D.选项A中的两角和的度数不能确定,选项B中∠1和∠2互补,选项C中∠1和∠2相等,选项D中∠1和∠2互余.
3.(2011·广州中考)已知∠α=26°,则∠α的补角是____度.
【解析】因为∠α=26°,所以∠α的补角是180°-26°=154°.
答案:154
【变式备选】一个角是35°39′,则它的余角为_______,补角为_______.
【解析】90°-35°39′=54°21′,
180°-35°39′=144°21′.
答案:54°21′ 144°21′
4.∠A与∠B互补,∠B与∠C互补,∠C=80°,则∠A的度数是________.
【解析】因为同角的补角相等,所以∠A=∠C=80°.
答案:80°
5.如图,O是直线AB上的点,OC是∠AOB的平分线,OD是一条射线,
∠AOD的补角是 ,余角是_______.
【解析】因为OC是∠AOB的平分线,
所以∠AOC=∠BOC=90°,
则∠AOD的补角是∠BOD,余角是∠COD.
答案:∠BOD ∠COD
6.∠A的余角和它的补角之比是1∶3,求∠A的度数.
【解析】设∠A的度数为x°,则180-x=3(90-x),
解得x=45.所以∠A的度数是45°.
题组二:方位角
1.在点O北偏西60°的某处有一点A,在点O南偏西20°的某处有一点B,则∠AOB的度数是( )
A.100° B.70° C.180° D.140°
【解析】选A.如图,∠AOB=180°-20°-60°=100°.
2.从A看B的方向是北偏东21°,那么从B看A的方向是( )
A.南偏东69° B.南偏西69°
C.南偏东21° D.南偏西21°
【解析】选D.如图,可知A点在B点的南偏西21°.
3.如图,点A,B在点O的方向分别是________.
【解析】由图可知点A在点O的北偏东30°,点B在点O的南偏东15°.
答案:北偏东30°,南偏东15°
4.画出射线OA,使射线OA在北偏西45°的方向上.
【解析】如图所示.
5.如图,一只蚂蚁从O点出发,沿东北方向爬行2.5 cm碰到障碍物B后,折向北偏西60°的方向爬行3 cm到C.
(1)画出蚂蚁的爬行路线.
(2)求出∠OBC的度数.
【解析】(1)先以O为顶点,表示正北方向的射线为角的一边,画45°的角,使它的一边OB′落在东与北之间,在射线OB′上取OB等于2.5 cm,同理以B点为顶点,画出BC=3 cm,则OB,BC是蚂蚁所爬行的路线.
如图所示:
(2)由题意知,点O在点B的西南方向,
所以∠DBO=45°,
因为∠CBE=60°,所以∠CBD=30°,
所以∠OBC=∠CBD+∠DBO
=30°+45°=75°.
【想一想错在哪?】如图,O是直线AB
上一点,OC为任意一条射线,OD平分
∠BOC,OE平分∠AOC.
(1)指出图中∠AOD与∠BOE的补角.
(2)试说明∠COD与∠COE具有怎样的数量关系.
提示:(1)本题找补角不全,互补的两个角与位置没有关系,不能只考虑图形中和是平角的两个角互补,还应该考虑和是180°的两个角也互补.(2)补角的性质是等角的补角相等,应用的条件是要考虑已知的两个角是不是相等.
