2020秋沪科版九年级数学上册第21章二次函数与反比例函数单元培优测试卷(Word版 含解析)
文档属性
| 名称 | 2020秋沪科版九年级数学上册第21章二次函数与反比例函数单元培优测试卷(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 294.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-25 12:10:01 | ||
图片预览



文档简介
2020秋沪科版九年级数学上册第21章二次函数与反比例函数单元培优测试卷
一、选择题(共10题;共40分)
1.反比例函数
经过点
,则下列说法错误的是(???
)
A.????
B.?函数图象分布在第一、三象限
C.?当
时,
随
的增大而增大???D.?当
时,
随
的增大而减小
2.在同一平面直角坐标系中,先将抛物线A:y=x2﹣2通过左右平移得到抛物线B,再将抛物线B通过上下平移得到抛物线C:y=x2﹣2x+2,则抛物线B的顶点坐标为(??
)
A.?(﹣1,2)??B.?(1,2)????C.?(1,﹣2)????D.?(﹣1,﹣2)
3.二次函数y=ax2+bx+c
图象如图所示,反比例函数y=
与一次函数y=bx+c在同一坐标系中大致图象是(??
)
A.??B.??C.?D.?
4.如图,点A是反比例函数
图象上的一点,过点A作
轴,垂足为点C
,
D为AC的中点,若
的面积为1,则k的值为(???
)
A.?????B.??????C.?3?????D.?4
5.如图,函数
与函数
的图象相交于点
.若
,则x的取值范围是(??
)
A.?
或
?????B.?
或
C.?
或
???D.?
或
6.如图,抛物线
交x轴于点A,B,交
轴于点C.若点A坐标为
,对称轴为直线
,则下列结论错误的是(???
)
A.二次函数的最大值为
?B.??C.?D.
7.某商人将单价为8元的商品按每件10元出售,每天可销售100件,已知这种商品每提高2元,其销量就要减少10件,为了使每天所赚利润最多,该商人应将销售价(为偶数)提高(??
)
A.?8元或10元???B.?12元???C.?8元????D.?10元
8.已知二次函数
,当x取互为相反数的任意两个实数值时,对应的函数值y总相等,则关于x的一元二次方程
的两根之积为(???
)
A.?0???B.?????C.??????D.?
9.如图,点A在反比例函数
的图象上,过点A作
轴,垂足为B,交反比例函数
的图象于点C.P为y轴上一点,连接
,
.则
的面积为(???
)
A.?5?????B.?6?????C.?11???????D.?12
10.关于二次函数
的三个结论:①对任意实数m,都有
与
对应的函数值相等;②若3≤x≤4,对应的y的整数值有4个,则
或
;③若抛物线与x轴交于不同两点A,B,且AB≤6,则
或
.其中正确的结论是(??
)
A.?①②???????B.?①③????????C.?②③??????D.?①②③
二、填空题(共4题;共20分)
11.如图,点A是反比例函数
图象上的一点,
垂直于x轴,垂足为B.
的面积为6.若点
也在此函数的图象上,则
________.
12.在平面直角坐标系中,点A(﹣2,1),B(3,2),C(﹣6,m)分别在三个不同的象限.若反比例函数y=
(k≠0)的图象经过其中两点,则m的值为________.
13.如图,抛物线y=ax2+bx+c(a>0)的对称轴是直线x=1,且经过点P(3,0),则a﹣b+c的值为________.
14.二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论:
①4a+b=0;②9a+c>3b;③,3a+c>0;④当x>﹣1时,y的值随x值的增大而增大.⑤
(m为任意实数)其中正确的结论有________.(填序号)
三、解答题(共2题;共16分)
15.已知抛物线
的对称轴为
,
是抛物线上一点,求该抛物线的解析式.
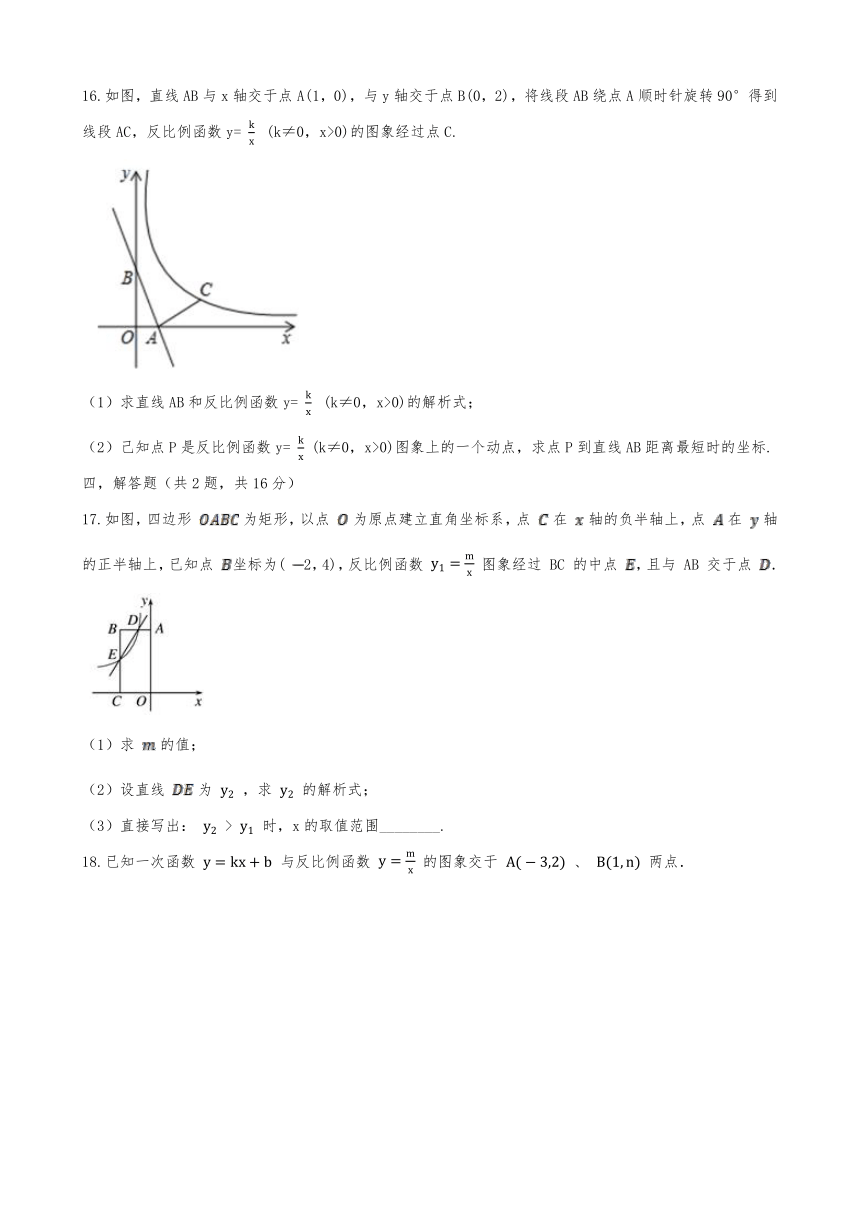
16.如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,2),将线段AB绕点A顺时针旋转90°得到线段AC,反比例函数y=
?(k≠0,x>0)的图象经过点C.
(1)求直线AB和反比例函数y=
?(k≠0,x>0)的解析式;
(2)己知点P是反比例函数y=
(k≠0,x>0)图象上的一个动点,求点P到直线AB距离最短时的坐标.
四,解答题(共2题,共16分)
17.如图,四边形
?为矩形,以点
?为原点建立直角坐标系,点
?在
?轴的负半轴上,点
?在
?轴的正半轴上,已知点
坐标为(
2,4),反比例函数
图象经过
BC
的中点
,且与
AB
交于点
.
(1)求
?的值;
(2)设直线
?为
,求
的解析式;
(3)直接写出:
>
时,x的取值范围________.
18.已知一次函数
与反比例函数
的图象交于
、
两点.
(1)求一次函数和反比例函数的表达式;
(2)求
的面积;
(3)点P在x轴上,当
为等腰三角形时,直接写出点P的坐标.
五、解答题(共2题,共20分)
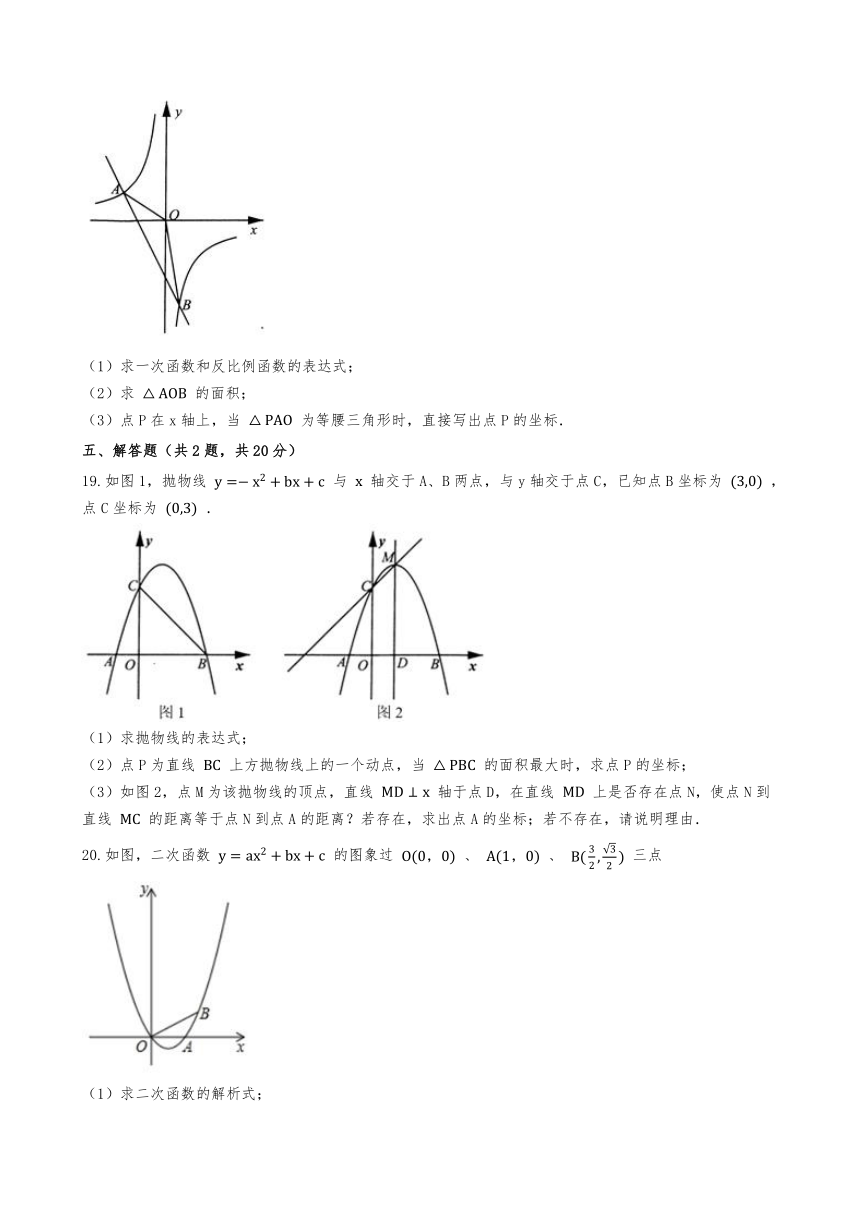
19.如图1,抛物线
与
轴交于A、B两点,与y轴交于点C,已知点B坐标为
,点C坐标为
.
(1)求抛物线的表达式;
(2)点P为直线
上方抛物线上的一个动点,当
的面积最大时,求点P的坐标;
(3)如图2,点M为该抛物线的顶点,直线
轴于点D,在直线
上是否存在点N,使点N到直线
的距离等于点N到点A的距离?若存在,求出点A的坐标;若不存在,请说明理由.
20.如图,二次函数
的图象过
、
、
三点
(1)求二次函数的解析式;
(2)若线段OB的垂直平分线与y轴交于点C,与二次函数的图象在x轴上方的部分相交于点D,求直线CD的解析式;
(3)在直线CD下方的二次函数的图象上有一动点P,过点P作
轴,交直线CD于Q,当线段PQ的长最大时,求点P的坐标.
六、解答题(共12分)
21.如图,在平面直角坐标系
中,反比例函数
的图像经过点
,点B在y轴的负半轴上,
交x轴于点C,C为线段
的中点.
(1)
________,点
的坐标为________;
(2)若点D为线段
上的一个动点,过点D作
轴,交反比例函数图像于点E,求
面积的最大值.
七、解答题(共12分)
22.已知二次函数
的图象与x轴交于
两点,与y轴交于点
,
(1)求二次函数的表达式及A点坐标;
(2)D是二次函数图象上位于第三象限内的点,求点D到直线
的距离取得最大值时点D的坐标;
(3)M是二次函数图象对称轴上的点,在二次函数图象上是否存在点N.使以
为顶点的四边形是平行四边形?若有,请写出点N的坐标(不写求解过程).
八、解答题(共14分)
23.如图,在平面直角坐标系中,已知抛物线y=x2+bx+c与直线AB相交于A,B两点,其中A(﹣3,﹣4),B(0,﹣1).
(1)求该抛物线的函数表达式;
(2)点P为直线AB下方抛物线上的任意一点,连接PA,PB,求△PAB面积的最大值;
(3)将该抛物线向右平移2个单位长度得到抛物线y=a1x2+b1x+c1(a1≠0),平移后的抛物线与原抛物线相交于点C,点D为原抛物线对称轴上的一点,在平面直角坐标系中是否存在点E,使以点B,C,D,E为顶点的四边形为菱形,若存在,请直接写出点E的坐标;若不存在,请说明理由.
答案
一、选择题
1.将点(2,1)代入
中,解得:k=2,A.k=2,不符合题意;
B.k=2﹥0,反比例函数图象分布在第一、三象限,不符合题意;
C.k=2﹥0且x﹥0,函数图象位于第一象限,且y随x的增大而减小,符合题意;
D.k=2﹥0且x﹥0,函数图象位于第一象限,且y随x的增大而减小,不符合题意;
故答案为:C.
2.解:抛物线A:y=x2﹣2的顶点坐标是(0,﹣2),抛物线C:y=x2﹣2x+2=(x﹣1)2+1的顶点坐标是(1,1).
则将抛物线A向右平移1个单位,再向上平移3个单位得到抛物线C.
所以抛物线B是将抛物线A向右平移1个单位得到的,其解析式为y=(x﹣1)2﹣2,
所以其顶点坐标是(1,﹣2).
故答案为:C.
3.解:由题意,得:a>0,b<0,c>0,
∴y=
的图象在第一、三象限,y=bx+c的图象经过第一、二、四象限,
观察各选项可知:只有C选项符合题意.
故答案为:C.
4.点A的坐标为(m,2n),
∴
,
∵D为AC的中点,
∴D(m,n),
∵AC⊥
轴,△ADO的面积为1,
∴
,
∴
,
∴
,
故答案为:D.
5.解:如图所示,直线图象在反比例函数图象之上的x的取值范围为
或
,
故答案为:
或
.
故答案为:D
6.解:抛物线y=ax2+bx+c过点A(?4,0),对称轴为直线x=?1,
因此有:x=?1=?
,即2a?b=0,因此选项D不符合题意;
当x=?1时,y=a?b+c的值最大,选项A符合题意;
由抛物线的对称性可知,抛物线与x轴的另一个交点为(2,0),
当x=1时,y=a+b+c>0,因此选项B符合题意;
抛物线与x轴有两个不同交点,因此b2?4ac>0,C符合题意;
故答案为:D.
7.解:(1)依题意,得y=(x﹣8)?(100﹣10×
)=﹣x2+190x﹣1200
=﹣5(x﹣19)2+605,﹣5<0,
∴抛物线开口向下,函数有最大值,
即当x=19时,y的最大值为605,
∵售价为偶数,
∴x为18或20,
当x=18时,y=600,
当x=20时,y=600,
∴x为18或20时y的值相同,
∴商品提高了18﹣10=8(元)或20﹣10=10(元)
故答案为:A.
8.解:∵二次函数
,
当x取互为相反数的任意两个实数值时,对应的函数值y总相等,
可知二次函数图像的对称轴为直线x=0,即y轴,
则
,
解得:a=-2,
则关于x的一元二次方程
为
,
则两根之积为
,
故答案为:D.
9.解:连接OA和OC,
∵点P在y轴上,则△AOC和△APC面积相等,
∵A在
上,C在
上,AB⊥x轴,
∴S△AOC=S△OAB-S△OBC=6,
∴△APC的面积为6,
故答案为:B.
10.解:∵抛物线的对称轴为
,
∴x1=2+m与x2=2-m关于直线x=2对称,
∴对任意实数m,都有x1=2+m与x2=2-m对应的函数值相等;
故①符合题意;
当x=3时,y=-3a-5,当x=4时,y=-5,
若a>0时,当3≤x≤4时,-3a-5<y≤-5,
∵当3≤x≤4时,对应的y的整数值有4个,
∴
,
若a<0时,当3≤x≤4时,-5≤y<-3a-5,
∵当3≤x≤4时,对应的y的整数值有4个,
∴
,
故②符合题意;
若a>0,抛物线与x轴交于不同两点A,B,且AB≤6,
∴△>0,25a-20a-5≥0,
∴
,
∴
;
若a<0,抛物线与x轴交于不同两点A,B,且AB≤6,
∴△>0,25a-20a-5≤0,
∴
∴a<
,
综上所述:当a<
或a≥1时,抛物线与x轴交于不同两点A,B,且AB≤6.
故③符合题意;
故答案为:D.
二、填空题
11.解:
的面积为6.
?
>
,
?
?
把
代入
?
?
经检验:
符合题意.
故答案为:
12.解:
点
,
,
分别在三个不同的象限,点
在第二象限,
点
一定在第三象限,
在第一象限,反比例函数
的图象经过其中两点,
反比例函数
的图象经过
,
,
,
,
故答案为:-1.
13.
0
由题意可知,抛物线的对称轴为x=1,且经过点P(3,0),
∴抛物线与x轴的另一个交点是(-1,0),
代入抛物线解析式y=ax2+bx+c中,得a-b+c=0.
故答案为:0.
14.
①③⑤
解:∵抛物线的对称轴为直线x=
=2,
∴b=?4a,即4a+b=0,所以①正确;
∵x=?3时,y<0,
∴9a?3b+c<0,即9a+c<3b,所以②错误;
∵抛物线与x轴的一个交点为(?1,0),
∴x=?1时,a?b+c=0,
∴a+4a+c=0,
∴3a+c=-2a,
∵a<0,
∴3a+c=-2a>0,所以③正确;
∵抛物线的对称轴为直线x=2,开口向下,
∴当-1<x<2时,函数值随x增大而增大,所以④错误;
∵b=?4a,
∴
=
,
∴
,∴⑤正确.
故答案为:①③⑤.
解答题
15.解:因为
的对称轴为
,
所以
.解得
.
又因为
是抛物线上一点,
所以
.
解得
.
所以抛物线的解析式为
.
16.
(1)解:将点A(1,0),点B(0,2),代入y=mx+b,
?
∴b=2,m=-2,
?
∴y=-2x+2;
?
∵过点C作CD⊥x轴,
∵线段AB绕点A顺时针旋转90°得到线段AC,
∴△ABO≌△CAD(AAS),
∴AD=AB=2,CD=OA=1,
∴C(3,1),
∴k=3,
∴y=
;
(2)解:设与AB平行的直线y=-2x+h,
联立-2x+b=
,
∴-2x2+bx-3=0,
当△=b2-24=0时,b=±2
,此时点P到直线AB距离最短;
∴P(
,
)
17.
(1)解:∵四边形
?为矩形
点
?坐标为(
2,4)
为
BC
的中点
∴点E坐标(-2,2)
∴
即
?
(2)(2)由题意得,点D坐标为(-1,4),
点E坐标(-2,2)
设
因为
,
,
设直线
?的解析式为
?,
所以
?
解得
?
所以
(3)
解:(3)反比例函数与直线y=2x+6相交于点D(-1,4)
,
E(-2,2)
,
根据图象可知:当-2<x<-1时,直线y=2x+6的图象在反比例函数的上边,
∴当-2<x<-1时,y2>y1.
18.
(1)解:将
代入
中,得
,
反比例函数的表达式为
在
的图象上,
,即
将
、
坐标代入
得
,解得:
.
一次函数表达式为:
(2)解:设直线
与
轴交于点C,则点
为
,
.
(3)解:
,
设P(x,0).
当AO=OP=
时,点
在
轴上,
点
为
或
当AO=AP=
时,
?,
x=-6或0(舍去)
点
为
,
当OP=AP时,
,
;
点
为
综上所述,符合条件的点P的坐标是
,
,
,
.
19.
(1)解:由题意得:
,
解得
,
抛物线的解析式为
(2)解:设点P的坐标为
,过点
作
轴于点H,交
于点G,
点
,
,
直线
的解析式为:
,
点G为
,
.
,
当
时,
最大,此时点
坐标为
.
(3)解:存在点N满足要求.
,
顶点M为
,
直线
的表达式为:
.设直线
与x轴交于点E,则点E为
,
,
.
设满足要求的点N坐标为
,则
.
过点N作
于点G,则
,
,
,而
,
,
整理得
,
解得
.
存在点N满足要求,点N坐标为
或
.
20.
(1)解:把
、
、
代入
得
解得
∴二次函数的解析式为
;
(2)解:如图,∵
,
∴其中点E的坐标为
设直线OB的解析式为y=kx
把
代入得
解得k=
∴直线OB的解析式为y=
x,
∵直线CD垂直平分OB,
∴可设直线CD的解析式为y=-
x+m,
把E
代入得
解得m=
∴直线CD的解析式为y=-
x+
;
(3)解:联立
得到
解得x1=-
,x2=1,
设P的横坐标为t,则P(t,
),
∵过点P作
轴,交直线CD于Q,
∴Q(t,-
t+
)
∴PQ=(-
t+
)-(
)=-
故当t=-
时PQ有最大值
此时P的坐标为(-
,
).
21.
(1)6;(2,0)
(2)解:设直线
对应的函数表达式为
.
将
,
代入得
,解得
.
所以直线
对应的函数表达式为
.
因为点
在线段
上,可设
,
因为
轴,交反比例函数图像于点E.所以
.
所以
.
所以当a=1时,
面积的最大值为
.
解:把点
代入反比例函数
,得:
,
解得:m=6,
∵A点横坐标为:4,B点横坐标为0,故C点横坐标为:
,
故答案为:6,
;
22.
(1)解:∵二次函数
图像与
轴的交点为B(1,0),与
轴交于点
,
∴将C代入,得:c=-3,则
,
∴方程
对应的两根之积为-3,
又B(1,0),
可得A(-3,0),将A,B两点代入二次函数,得:
,
解得:
,
∴二次函数表达式为:
;
(2)解:当点D到直线
的距离取得最大值时,
∵A(-3,0),
,
设直线AC的表达式为:y=kx+n,,将A和C代入,
,解得:
,
∴直线AC的表达式为y=-x-3,将直线AC向下平移m(m>0)个单位,得到直线l,
当直线l与二次函数图像只有一个交点时,该交点为点D,此时点D到直线AC的距离最大,
此时直线l的表达式为y=-x-3-m,
联立:
,得:
,
令△=
,解得:m=
,
则解方程:
,得x=
,
∴点D的坐标为(
,
)
(3)解:∵M在抛物线对称轴上,设M坐标为(-1,t),
当OB为平行四边形的边时,
如图1,可知MN和OB平行且相等,
∴点N(-2,t)或(0,t),代入抛物线表达式得:
解得:t=-3,
∴N(-2,-3)或(0,-3);
当OB为平行四边形对角线时,
线段OB的中点为(
,0),对角线MN的中点也为(
,0),
∵M坐标为(-1,t),
可得点N(2,-t),代入抛物线表达式得:
4+4-3=-t,
解得:t=-5,
∴点N的坐标为(2,-5),
综上:以
为顶点的四边形是平行四边形时,点N的坐标为(-2,-3)或(0,-3)或(2,-5).
23.
(1)解:将点A、B的坐标代入抛物线表达式得
,解得
,
故抛物线的表达式为:y=x2+4x﹣1;
(2)解:设直线AB的表达式为:y=kx+t,则
,解得
,
故直线AB的表达式为:y=x﹣1,
过点P作y轴的平行线交AB于点H,
设点P(x,x2+4x﹣1),则H(x,x﹣1),
△PAB面积S=
×PH×(xB﹣xA)=
(x﹣1﹣x2﹣4x+1)×(0+3)=﹣
x2﹣
x,
∵
<0,故S有最大值,当x=﹣
时,S的最大值为
;
(3)解:抛物线的表达式为:y=x2+4x﹣1=(x+2)2﹣5,
则平移后的抛物线表达式为:y=x2﹣5,
联立上述两式并解得:
,故点C(﹣1,﹣4);
设点D(﹣2,m)、点E(s,t),而点B、C的坐标分别为(0,﹣1)、(﹣1,﹣4);
①当BC为菱形的边时,
点C向右平移1个单位向上平移3个单位得到B,同样D(E)向右平移1个单位向上平移3个单位得到E(D),
即﹣2+1=s且m+3=t①或﹣2﹣1=s且m﹣3=t②,
当点D在E的下方时,则BE=BC,即s2+(t+1)2=12+32③,
当点D在E的上方时,则BD=BC,即22+(m+1)2=12+32④,
联立①③并解得:s=﹣1,t=2或﹣4(舍去﹣4),故点E(﹣1,3);
联立②④并解得:s=1,t=﹣4±
,故点E(1,﹣4
)或(1,﹣4﹣
);
②当BC为菱形的的对角线时,
则由中点公式得:﹣1=s﹣2且﹣4﹣1=m+t⑤,
此时,BD=BE,即22+(m+1)2=s2+(t+1)2⑥,
联立⑤⑥并解得:s=1,t=﹣3,
故点E(1,﹣3),
综上,点E的坐标为:(﹣1,2)或(1,﹣4
)或(1,﹣4﹣
)或(1,﹣3).
一、选择题(共10题;共40分)
1.反比例函数
经过点
,则下列说法错误的是(???
)
A.????
B.?函数图象分布在第一、三象限
C.?当
时,
随
的增大而增大???D.?当
时,
随
的增大而减小
2.在同一平面直角坐标系中,先将抛物线A:y=x2﹣2通过左右平移得到抛物线B,再将抛物线B通过上下平移得到抛物线C:y=x2﹣2x+2,则抛物线B的顶点坐标为(??
)
A.?(﹣1,2)??B.?(1,2)????C.?(1,﹣2)????D.?(﹣1,﹣2)
3.二次函数y=ax2+bx+c
图象如图所示,反比例函数y=
与一次函数y=bx+c在同一坐标系中大致图象是(??
)
A.??B.??C.?D.?
4.如图,点A是反比例函数
图象上的一点,过点A作
轴,垂足为点C
,
D为AC的中点,若
的面积为1,则k的值为(???
)
A.?????B.??????C.?3?????D.?4
5.如图,函数
与函数
的图象相交于点
.若
,则x的取值范围是(??
)
A.?
或
?????B.?
或
C.?
或
???D.?
或
6.如图,抛物线
交x轴于点A,B,交
轴于点C.若点A坐标为
,对称轴为直线
,则下列结论错误的是(???
)
A.二次函数的最大值为
?B.??C.?D.
7.某商人将单价为8元的商品按每件10元出售,每天可销售100件,已知这种商品每提高2元,其销量就要减少10件,为了使每天所赚利润最多,该商人应将销售价(为偶数)提高(??
)
A.?8元或10元???B.?12元???C.?8元????D.?10元
8.已知二次函数
,当x取互为相反数的任意两个实数值时,对应的函数值y总相等,则关于x的一元二次方程
的两根之积为(???
)
A.?0???B.?????C.??????D.?
9.如图,点A在反比例函数
的图象上,过点A作
轴,垂足为B,交反比例函数
的图象于点C.P为y轴上一点,连接
,
.则
的面积为(???
)
A.?5?????B.?6?????C.?11???????D.?12
10.关于二次函数
的三个结论:①对任意实数m,都有
与
对应的函数值相等;②若3≤x≤4,对应的y的整数值有4个,则
或
;③若抛物线与x轴交于不同两点A,B,且AB≤6,则
或
.其中正确的结论是(??
)
A.?①②???????B.?①③????????C.?②③??????D.?①②③
二、填空题(共4题;共20分)
11.如图,点A是反比例函数
图象上的一点,
垂直于x轴,垂足为B.
的面积为6.若点
也在此函数的图象上,则
________.
12.在平面直角坐标系中,点A(﹣2,1),B(3,2),C(﹣6,m)分别在三个不同的象限.若反比例函数y=
(k≠0)的图象经过其中两点,则m的值为________.
13.如图,抛物线y=ax2+bx+c(a>0)的对称轴是直线x=1,且经过点P(3,0),则a﹣b+c的值为________.
14.二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论:
①4a+b=0;②9a+c>3b;③,3a+c>0;④当x>﹣1时,y的值随x值的增大而增大.⑤
(m为任意实数)其中正确的结论有________.(填序号)
三、解答题(共2题;共16分)
15.已知抛物线
的对称轴为
,
是抛物线上一点,求该抛物线的解析式.
16.如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,2),将线段AB绕点A顺时针旋转90°得到线段AC,反比例函数y=
?(k≠0,x>0)的图象经过点C.
(1)求直线AB和反比例函数y=
?(k≠0,x>0)的解析式;
(2)己知点P是反比例函数y=
(k≠0,x>0)图象上的一个动点,求点P到直线AB距离最短时的坐标.
四,解答题(共2题,共16分)
17.如图,四边形
?为矩形,以点
?为原点建立直角坐标系,点
?在
?轴的负半轴上,点
?在
?轴的正半轴上,已知点
坐标为(
2,4),反比例函数
图象经过
BC
的中点
,且与
AB
交于点
.
(1)求
?的值;
(2)设直线
?为
,求
的解析式;
(3)直接写出:
>
时,x的取值范围________.
18.已知一次函数
与反比例函数
的图象交于
、
两点.
(1)求一次函数和反比例函数的表达式;
(2)求
的面积;
(3)点P在x轴上,当
为等腰三角形时,直接写出点P的坐标.
五、解答题(共2题,共20分)
19.如图1,抛物线
与
轴交于A、B两点,与y轴交于点C,已知点B坐标为
,点C坐标为
.
(1)求抛物线的表达式;
(2)点P为直线
上方抛物线上的一个动点,当
的面积最大时,求点P的坐标;
(3)如图2,点M为该抛物线的顶点,直线
轴于点D,在直线
上是否存在点N,使点N到直线
的距离等于点N到点A的距离?若存在,求出点A的坐标;若不存在,请说明理由.
20.如图,二次函数
的图象过
、
、
三点
(1)求二次函数的解析式;
(2)若线段OB的垂直平分线与y轴交于点C,与二次函数的图象在x轴上方的部分相交于点D,求直线CD的解析式;
(3)在直线CD下方的二次函数的图象上有一动点P,过点P作
轴,交直线CD于Q,当线段PQ的长最大时,求点P的坐标.
六、解答题(共12分)
21.如图,在平面直角坐标系
中,反比例函数
的图像经过点
,点B在y轴的负半轴上,
交x轴于点C,C为线段
的中点.
(1)
________,点
的坐标为________;
(2)若点D为线段
上的一个动点,过点D作
轴,交反比例函数图像于点E,求
面积的最大值.
七、解答题(共12分)
22.已知二次函数
的图象与x轴交于
两点,与y轴交于点
,
(1)求二次函数的表达式及A点坐标;
(2)D是二次函数图象上位于第三象限内的点,求点D到直线
的距离取得最大值时点D的坐标;
(3)M是二次函数图象对称轴上的点,在二次函数图象上是否存在点N.使以
为顶点的四边形是平行四边形?若有,请写出点N的坐标(不写求解过程).
八、解答题(共14分)
23.如图,在平面直角坐标系中,已知抛物线y=x2+bx+c与直线AB相交于A,B两点,其中A(﹣3,﹣4),B(0,﹣1).
(1)求该抛物线的函数表达式;
(2)点P为直线AB下方抛物线上的任意一点,连接PA,PB,求△PAB面积的最大值;
(3)将该抛物线向右平移2个单位长度得到抛物线y=a1x2+b1x+c1(a1≠0),平移后的抛物线与原抛物线相交于点C,点D为原抛物线对称轴上的一点,在平面直角坐标系中是否存在点E,使以点B,C,D,E为顶点的四边形为菱形,若存在,请直接写出点E的坐标;若不存在,请说明理由.
答案
一、选择题
1.将点(2,1)代入
中,解得:k=2,A.k=2,不符合题意;
B.k=2﹥0,反比例函数图象分布在第一、三象限,不符合题意;
C.k=2﹥0且x﹥0,函数图象位于第一象限,且y随x的增大而减小,符合题意;
D.k=2﹥0且x﹥0,函数图象位于第一象限,且y随x的增大而减小,不符合题意;
故答案为:C.
2.解:抛物线A:y=x2﹣2的顶点坐标是(0,﹣2),抛物线C:y=x2﹣2x+2=(x﹣1)2+1的顶点坐标是(1,1).
则将抛物线A向右平移1个单位,再向上平移3个单位得到抛物线C.
所以抛物线B是将抛物线A向右平移1个单位得到的,其解析式为y=(x﹣1)2﹣2,
所以其顶点坐标是(1,﹣2).
故答案为:C.
3.解:由题意,得:a>0,b<0,c>0,
∴y=
的图象在第一、三象限,y=bx+c的图象经过第一、二、四象限,
观察各选项可知:只有C选项符合题意.
故答案为:C.
4.点A的坐标为(m,2n),
∴
,
∵D为AC的中点,
∴D(m,n),
∵AC⊥
轴,△ADO的面积为1,
∴
,
∴
,
∴
,
故答案为:D.
5.解:如图所示,直线图象在反比例函数图象之上的x的取值范围为
或
,
故答案为:
或
.
故答案为:D
6.解:抛物线y=ax2+bx+c过点A(?4,0),对称轴为直线x=?1,
因此有:x=?1=?
,即2a?b=0,因此选项D不符合题意;
当x=?1时,y=a?b+c的值最大,选项A符合题意;
由抛物线的对称性可知,抛物线与x轴的另一个交点为(2,0),
当x=1时,y=a+b+c>0,因此选项B符合题意;
抛物线与x轴有两个不同交点,因此b2?4ac>0,C符合题意;
故答案为:D.
7.解:(1)依题意,得y=(x﹣8)?(100﹣10×
)=﹣x2+190x﹣1200
=﹣5(x﹣19)2+605,﹣5<0,
∴抛物线开口向下,函数有最大值,
即当x=19时,y的最大值为605,
∵售价为偶数,
∴x为18或20,
当x=18时,y=600,
当x=20时,y=600,
∴x为18或20时y的值相同,
∴商品提高了18﹣10=8(元)或20﹣10=10(元)
故答案为:A.
8.解:∵二次函数
,
当x取互为相反数的任意两个实数值时,对应的函数值y总相等,
可知二次函数图像的对称轴为直线x=0,即y轴,
则
,
解得:a=-2,
则关于x的一元二次方程
为
,
则两根之积为
,
故答案为:D.
9.解:连接OA和OC,
∵点P在y轴上,则△AOC和△APC面积相等,
∵A在
上,C在
上,AB⊥x轴,
∴S△AOC=S△OAB-S△OBC=6,
∴△APC的面积为6,
故答案为:B.
10.解:∵抛物线的对称轴为
,
∴x1=2+m与x2=2-m关于直线x=2对称,
∴对任意实数m,都有x1=2+m与x2=2-m对应的函数值相等;
故①符合题意;
当x=3时,y=-3a-5,当x=4时,y=-5,
若a>0时,当3≤x≤4时,-3a-5<y≤-5,
∵当3≤x≤4时,对应的y的整数值有4个,
∴
,
若a<0时,当3≤x≤4时,-5≤y<-3a-5,
∵当3≤x≤4时,对应的y的整数值有4个,
∴
,
故②符合题意;
若a>0,抛物线与x轴交于不同两点A,B,且AB≤6,
∴△>0,25a-20a-5≥0,
∴
,
∴
;
若a<0,抛物线与x轴交于不同两点A,B,且AB≤6,
∴△>0,25a-20a-5≤0,
∴
∴a<
,
综上所述:当a<
或a≥1时,抛物线与x轴交于不同两点A,B,且AB≤6.
故③符合题意;
故答案为:D.
二、填空题
11.解:
的面积为6.
?
>
,
?
?
把
代入
?
?
经检验:
符合题意.
故答案为:
12.解:
点
,
,
分别在三个不同的象限,点
在第二象限,
点
一定在第三象限,
在第一象限,反比例函数
的图象经过其中两点,
反比例函数
的图象经过
,
,
,
,
故答案为:-1.
13.
0
由题意可知,抛物线的对称轴为x=1,且经过点P(3,0),
∴抛物线与x轴的另一个交点是(-1,0),
代入抛物线解析式y=ax2+bx+c中,得a-b+c=0.
故答案为:0.
14.
①③⑤
解:∵抛物线的对称轴为直线x=
=2,
∴b=?4a,即4a+b=0,所以①正确;
∵x=?3时,y<0,
∴9a?3b+c<0,即9a+c<3b,所以②错误;
∵抛物线与x轴的一个交点为(?1,0),
∴x=?1时,a?b+c=0,
∴a+4a+c=0,
∴3a+c=-2a,
∵a<0,
∴3a+c=-2a>0,所以③正确;
∵抛物线的对称轴为直线x=2,开口向下,
∴当-1<x<2时,函数值随x增大而增大,所以④错误;
∵b=?4a,
∴
=
,
∴
,∴⑤正确.
故答案为:①③⑤.
解答题
15.解:因为
的对称轴为
,
所以
.解得
.
又因为
是抛物线上一点,
所以
.
解得
.
所以抛物线的解析式为
.
16.
(1)解:将点A(1,0),点B(0,2),代入y=mx+b,
?
∴b=2,m=-2,
?
∴y=-2x+2;
?
∵过点C作CD⊥x轴,
∵线段AB绕点A顺时针旋转90°得到线段AC,
∴△ABO≌△CAD(AAS),
∴AD=AB=2,CD=OA=1,
∴C(3,1),
∴k=3,
∴y=
;
(2)解:设与AB平行的直线y=-2x+h,
联立-2x+b=
,
∴-2x2+bx-3=0,
当△=b2-24=0时,b=±2
,此时点P到直线AB距离最短;
∴P(
,
)
17.
(1)解:∵四边形
?为矩形
点
?坐标为(
2,4)
为
BC
的中点
∴点E坐标(-2,2)
∴
即
?
(2)(2)由题意得,点D坐标为(-1,4),
点E坐标(-2,2)
设
因为
,
,
设直线
?的解析式为
?,
所以
?
解得
?
所以
(3)
解:(3)反比例函数与直线y=2x+6相交于点D(-1,4)
,
E(-2,2)
,
根据图象可知:当-2<x<-1时,直线y=2x+6的图象在反比例函数的上边,
∴当-2<x<-1时,y2>y1.
18.
(1)解:将
代入
中,得
,
反比例函数的表达式为
在
的图象上,
,即
将
、
坐标代入
得
,解得:
.
一次函数表达式为:
(2)解:设直线
与
轴交于点C,则点
为
,
.
(3)解:
,
设P(x,0).
当AO=OP=
时,点
在
轴上,
点
为
或
当AO=AP=
时,
?,
x=-6或0(舍去)
点
为
,
当OP=AP时,
,
;
点
为
综上所述,符合条件的点P的坐标是
,
,
,
.
19.
(1)解:由题意得:
,
解得
,
抛物线的解析式为
(2)解:设点P的坐标为
,过点
作
轴于点H,交
于点G,
点
,
,
直线
的解析式为:
,
点G为
,
.
,
当
时,
最大,此时点
坐标为
.
(3)解:存在点N满足要求.
,
顶点M为
,
直线
的表达式为:
.设直线
与x轴交于点E,则点E为
,
,
.
设满足要求的点N坐标为
,则
.
过点N作
于点G,则
,
,
,而
,
,
整理得
,
解得
.
存在点N满足要求,点N坐标为
或
.
20.
(1)解:把
、
、
代入
得
解得
∴二次函数的解析式为
;
(2)解:如图,∵
,
∴其中点E的坐标为
设直线OB的解析式为y=kx
把
代入得
解得k=
∴直线OB的解析式为y=
x,
∵直线CD垂直平分OB,
∴可设直线CD的解析式为y=-
x+m,
把E
代入得
解得m=
∴直线CD的解析式为y=-
x+
;
(3)解:联立
得到
解得x1=-
,x2=1,
设P的横坐标为t,则P(t,
),
∵过点P作
轴,交直线CD于Q,
∴Q(t,-
t+
)
∴PQ=(-
t+
)-(
)=-
故当t=-
时PQ有最大值
此时P的坐标为(-
,
).
21.
(1)6;(2,0)
(2)解:设直线
对应的函数表达式为
.
将
,
代入得
,解得
.
所以直线
对应的函数表达式为
.
因为点
在线段
上,可设
,
因为
轴,交反比例函数图像于点E.所以
.
所以
.
所以当a=1时,
面积的最大值为
.
解:把点
代入反比例函数
,得:
,
解得:m=6,
∵A点横坐标为:4,B点横坐标为0,故C点横坐标为:
,
故答案为:6,
;
22.
(1)解:∵二次函数
图像与
轴的交点为B(1,0),与
轴交于点
,
∴将C代入,得:c=-3,则
,
∴方程
对应的两根之积为-3,
又B(1,0),
可得A(-3,0),将A,B两点代入二次函数,得:
,
解得:
,
∴二次函数表达式为:
;
(2)解:当点D到直线
的距离取得最大值时,
∵A(-3,0),
,
设直线AC的表达式为:y=kx+n,,将A和C代入,
,解得:
,
∴直线AC的表达式为y=-x-3,将直线AC向下平移m(m>0)个单位,得到直线l,
当直线l与二次函数图像只有一个交点时,该交点为点D,此时点D到直线AC的距离最大,
此时直线l的表达式为y=-x-3-m,
联立:
,得:
,
令△=
,解得:m=
,
则解方程:
,得x=
,
∴点D的坐标为(
,
)
(3)解:∵M在抛物线对称轴上,设M坐标为(-1,t),
当OB为平行四边形的边时,
如图1,可知MN和OB平行且相等,
∴点N(-2,t)或(0,t),代入抛物线表达式得:
解得:t=-3,
∴N(-2,-3)或(0,-3);
当OB为平行四边形对角线时,
线段OB的中点为(
,0),对角线MN的中点也为(
,0),
∵M坐标为(-1,t),
可得点N(2,-t),代入抛物线表达式得:
4+4-3=-t,
解得:t=-5,
∴点N的坐标为(2,-5),
综上:以
为顶点的四边形是平行四边形时,点N的坐标为(-2,-3)或(0,-3)或(2,-5).
23.
(1)解:将点A、B的坐标代入抛物线表达式得
,解得
,
故抛物线的表达式为:y=x2+4x﹣1;
(2)解:设直线AB的表达式为:y=kx+t,则
,解得
,
故直线AB的表达式为:y=x﹣1,
过点P作y轴的平行线交AB于点H,
设点P(x,x2+4x﹣1),则H(x,x﹣1),
△PAB面积S=
×PH×(xB﹣xA)=
(x﹣1﹣x2﹣4x+1)×(0+3)=﹣
x2﹣
x,
∵
<0,故S有最大值,当x=﹣
时,S的最大值为
;
(3)解:抛物线的表达式为:y=x2+4x﹣1=(x+2)2﹣5,
则平移后的抛物线表达式为:y=x2﹣5,
联立上述两式并解得:
,故点C(﹣1,﹣4);
设点D(﹣2,m)、点E(s,t),而点B、C的坐标分别为(0,﹣1)、(﹣1,﹣4);
①当BC为菱形的边时,
点C向右平移1个单位向上平移3个单位得到B,同样D(E)向右平移1个单位向上平移3个单位得到E(D),
即﹣2+1=s且m+3=t①或﹣2﹣1=s且m﹣3=t②,
当点D在E的下方时,则BE=BC,即s2+(t+1)2=12+32③,
当点D在E的上方时,则BD=BC,即22+(m+1)2=12+32④,
联立①③并解得:s=﹣1,t=2或﹣4(舍去﹣4),故点E(﹣1,3);
联立②④并解得:s=1,t=﹣4±
,故点E(1,﹣4
)或(1,﹣4﹣
);
②当BC为菱形的的对角线时,
则由中点公式得:﹣1=s﹣2且﹣4﹣1=m+t⑤,
此时,BD=BE,即22+(m+1)2=s2+(t+1)2⑥,
联立⑤⑥并解得:s=1,t=﹣3,
故点E(1,﹣3),
综上,点E的坐标为:(﹣1,2)或(1,﹣4
)或(1,﹣4﹣
)或(1,﹣3).
