北师大版数学八年级上册6.2 中位数与众数习题课件(33张)
文档属性
| 名称 | 北师大版数学八年级上册6.2 中位数与众数习题课件(33张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-25 00:00:00 | ||
图片预览









文档简介
名师导学
A. 一般地,n个数据按大小顺序排列,处于__________位置的一个数据(或最中间两个数据的__________)叫做这组数据的中位数.
1. 已知一组数据:2,1,7,4,5,这组数据的中位数是__________.
最中间
平均数
4
B. 一组数据中出现次数__________的那个数据叫做这组数据的众数. 一组数据的众数可能不止一个.
2. 已知一组数据:3,4,5,5,6,6,6,这组数据的众数是__________.
最多
6
课堂讲练
典型例题
新知1:中位数
【例1】已知数据:2,1,4,6,9,8,6,1,则这组数据的中位数是 ( )
A. 4 B. 6
C. 5 D. 4和6
C
模拟演练
1. 一组数据按从小到大排列为2,4,8,x,10,14. 若这组数据的中位数为9,则x是 ( )
A. 6 B. 8
C. 9 D. 10
D
典型例题
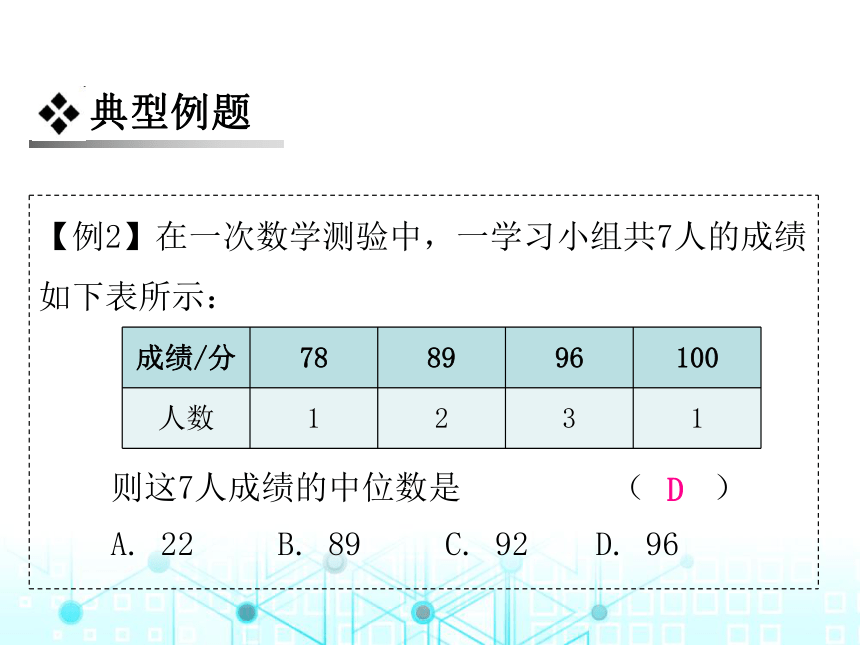
【例2】在一次数学测验中,一学习小组共7人的成绩如下表所示:
成绩/分
78
89
96
100
人数
1
2
3
1
则这7人成绩的中位数是 ( )
A. 22 B. 89 C. 92 D. 96
D
模拟演练
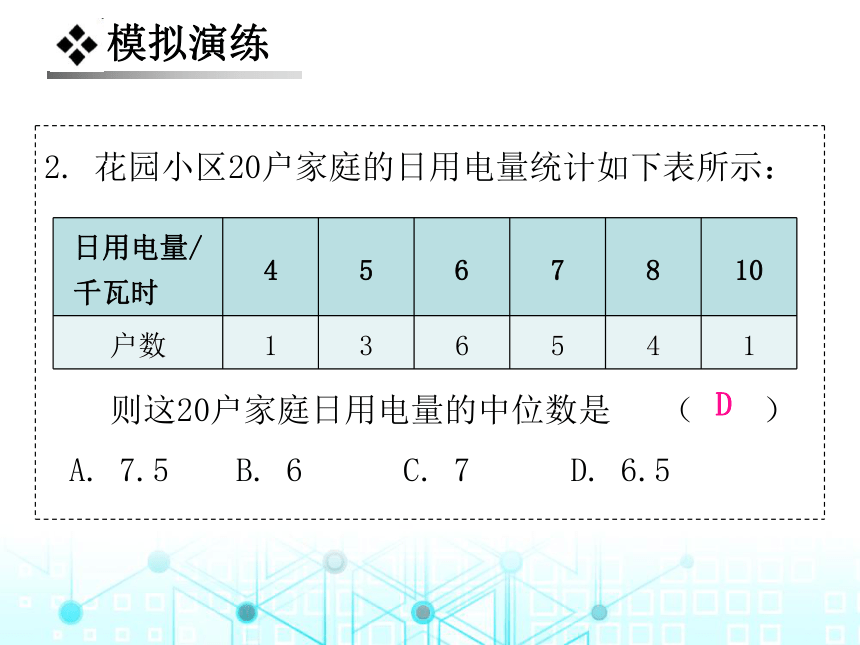
2. 花园小区20户家庭的日用电量统计如下表所示:
日用电量/千瓦时
4
5
6
7
8
10
户数
1
3
6
5
4
1
则这20户家庭日用电量的中位数是 ( )
A. 7.5 B. 6 C. 7 D. 6.5
D
典型例题
新知2:众数
【例3】某同学一周中每天完成家庭作业所花时间(单位:分钟)分别为:35,40,45,40,55,40,48,则这组数据的众数是 ( )
A. 35 B. 40 C. 45 D. 55
B
模拟演练
3. 已知一组数据6,3,x,4,4,5,6的众数是6,则x的值是__________.
6
【例4】九年级某班40位同学的年龄如下表所示:
年龄/岁
13
14
15
16
人数
3
16
19
2
则该班40名同学年龄的众数是__________岁.
15
典型例题
模拟演练
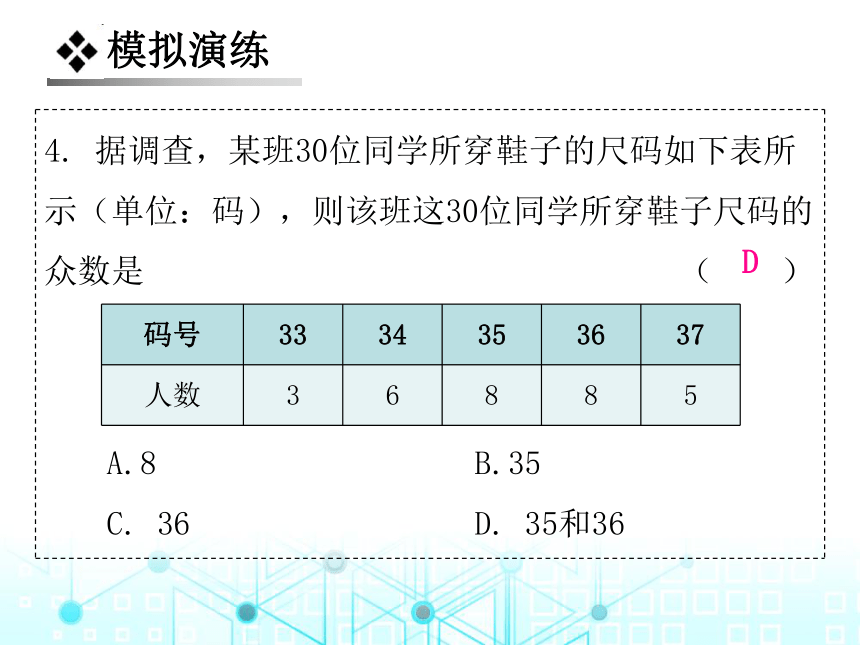
4. 据调查,某班30位同学所穿鞋子的尺码如下表所示(单位:码),则该班这30位同学所穿鞋子尺码的众数是 ( )
D
码号
33
34
35
36
37
人数
3
6
8
8
5
A.8 B.35
C. 36 D. 35和36
新知3:运用众数、中位数、平均数分析数据的集中趋势
【例5】某中学举办了一次以“我的中国梦”为主题的演讲比赛. 最后确定7名同学参加决赛,他们的决赛成绩各不相同,其中李华已经知道自己的成绩,但能否进前四名,他还必须清楚这7名同学成绩的__________(填“平均数”“众数”或“中位数”).
中位数
典型例题
5. 某商场为了统计某品牌运动鞋哪个尺码卖得最好,则应关注该品牌运动鞋各尺码销售数据的平均数、众数、中位数这三个数据中的__________.
模拟演练
众数
【例6】某学习兴趣小组参加一次单元测验,成绩统计情况如下表(单位:分):
分数
73
74
75
76
77
78
79
82
83
84
86
88
90
92
人数
1
1
5
4
3
2
3
1
1
1
2
3
1
2
典型例题
(1)该兴趣小组共有多少人?
(2)兴趣小组本次单元测试成绩的平均数、中位数、众数各是多少?
(3)老师打算为兴趣小组下单元考试设定一个新目标,学生达到或超过目标给予奖励,并希望小组三分之一左右的优秀学生得到奖励.请你帮老师从平均数、中位数、众数三个数中选择一个比较恰当的目标数.如果计划让一半左右的人都得到奖励,确定哪个数作为目标恰当些?
解:(1)该兴趣小组的总人数为1+1+5+4+3+2+3+1+1+1+2+3+1+2=30(人).
(2)本次单元测试成绩的平均数为
×73+74+75×5+76×4+77×3+78×2+79×3+82
+83+84+86×2+88×3+90+92×2)=80.3(分).表格中数据已经按照从小到大的顺序排列,一共有30个数,位于第15,第16的数都是78,所以中位数是(78+78)÷2=78(分).75出现了5次,次数最多,所以众数是75分.
(3)由(2)可知,平均数为80.3分,中位数为78分,众数为75分,如果希望小组三分之一左右的优秀学生得到奖励,老师可以选择平均数.如果计划让一半左右的人都得到奖励,确定中位数作为目标恰当些,因为中位数以上的人数占总人数的一半左右.
6. 某中学数学活动小组为了调查居民的用水情况,从某社区的1 500户家庭中随机抽取了30户家庭的月用水量,结果如下表所示:
模拟演练
月用水量/t
3
4
5
7
8
9
40
户数
4
3
5
11
4
2
1
(1)求这30户家庭月用水量的平均数、众数和中位数;
(2)根据上述数据,试估计该社区的月用水量;
(3)由于我国水资源缺乏,许多城市常利用分段计费的方法引导人们节约用水,即规定每个家庭的月基本用水量为m(t),家庭月用水量不超过m(t)的部分按原价收费,超过m(t)的部分加倍收费. 你认为上述问题中的平均数、众数和中位数中哪一个量作为月基本用水量比较合适?简述理由.
解:(1)这30户家庭月用水量的平均数为
×(3×4+4×3+5×5+7×11+8×4+9×2+ 40×1)=7.2(t).
因为7出现了11次,出现的次数最多,所以众数是7 t.
因为共有30个数,所以中位数是第15,第16个数的平均数,即中位数是(7+7)÷2=7(t).
(2)因为该社区共1 500户家庭,所以该社区的月用水量约为7.2×1 500=10 800(t).
(3)用众数或中位数作为月基本用水量比较合适,因为满足大多数家庭用水量的需求,而抽样的30户家庭的用水量存在较大数据,影响了平均数,故不宜采用平均数.
分层训练
【A组】
1. 在一组数据3,4,4,6,8中,下列说法错误的是
( )
A. 它的众数是4
B. 它的平均数是5
C. 它的中位数是5
D. 它的众数等于中位数
C
2. 某篮球兴趣小组7名学生参加投篮比赛,每人投10个,投中的个数分别为:8,5,7,5,8,6,8,则这组数据的众数和中位数分别为 ( )
A. 5,7 B. 6,7
C. 8,6 D. 8,7
D
3.广州市春季某一周的最高气温统计如下表:
则这组数据的中位数与众数分别是 ( )
A. 27,28 B. 27.5,28
C. 28,27 D. 26.5,27
最高气温/℃
25
26
27
28
天数
1
1
2
3
A
4. 已知数据x1,x2,x3,x4,…,xn的平均数是m,中位数是n,众数是t,则数据3x1+7,3x2+7,3x3+7,…,3xn+7的平均数是__________,中位数是__________,众数是__________.
3m+7
3n+7
3t+7
【B组】
5. 小强在最近的5场篮球赛中,得分分别为10,13,9,8,10分. 若小强下一场球赛得分是16分,则小强得分的平均数、中位数和众数中,发生改变的是__________.
平均数
6. 某服装店为调动营业员的积极性,决定实行目标管理,根据每月销售目标完成情况发放奖金. 该店统计了每位营业员前半年的月均销售额,并算出所得数据的平均数、众数、中位数,分别为22,15,18(单位:万元). 若想让一半左右的营业员都能达到月销售目标,则月销售额定为__________万元较为合适.
18
7. 某鞋店一周内销售了某种品牌的男鞋60双,各种尺码的销量统计如下:
由此你能给这家鞋店提供的进货建议是__________
_____________________________________________.
尺码/cm
23.5
24
24.5
25
25.5
26
26.5
销量/双
3
7
6
18
18
7
2
25 cm和
25.5 cm尺码的鞋子多进一些(合理即可)
【C组】
8. 甲、乙、丙三个家电厂家在广告中都声称,他们的某种电子产品在正常情况下的使用寿命都是8年,经质量检测部门对这三家销售的产品的使用寿命进行跟踪调查,统计结果如下(单位:年).
甲厂:4,5,5,5,5,7,9,12,13,15;
乙厂:6,6,8,8,8,9,10,12,14,15;
丙厂:4,4,4,6,7,9,13,15,16,16.
请回答下列问题.
(1)填空:
(2)这三个厂家的销售广告分别利用了哪一种数据表示集中趋势的特征数?
(3)如果你是顾客,你会买三家中哪一家的电子产品?为什么?
厂家
平均数
众数
中位数
甲厂
________
_______
6
乙厂
9.6
________
8.5
丙厂
9.4
4
_______
解:(1)
厂家
平均数
众数
中位数
甲厂
________
_______
6
乙厂
9.6
________
8.5
丙厂
9.4
4
_______
8
5
8
8
(2)甲厂家的销售广告利用了平均数“8”表示集中趋势的特征数;
乙厂家的销售广告利用了众数“8”表示集中趋势的特征数;
丙厂家的销售广告利用了中位数“8”表示集中趋势的特征数.
(3)通过(1)中表格可知平均数为乙>丙>甲;众数为乙>甲>丙;中位数为乙>丙>甲.
顾客在选购产品时,一般以平均数为依据,选平均数大的厂家的产品,因此应选乙厂家的产品.
A. 一般地,n个数据按大小顺序排列,处于__________位置的一个数据(或最中间两个数据的__________)叫做这组数据的中位数.
1. 已知一组数据:2,1,7,4,5,这组数据的中位数是__________.
最中间
平均数
4
B. 一组数据中出现次数__________的那个数据叫做这组数据的众数. 一组数据的众数可能不止一个.
2. 已知一组数据:3,4,5,5,6,6,6,这组数据的众数是__________.
最多
6
课堂讲练
典型例题
新知1:中位数
【例1】已知数据:2,1,4,6,9,8,6,1,则这组数据的中位数是 ( )
A. 4 B. 6
C. 5 D. 4和6
C
模拟演练
1. 一组数据按从小到大排列为2,4,8,x,10,14. 若这组数据的中位数为9,则x是 ( )
A. 6 B. 8
C. 9 D. 10
D
典型例题
【例2】在一次数学测验中,一学习小组共7人的成绩如下表所示:
成绩/分
78
89
96
100
人数
1
2
3
1
则这7人成绩的中位数是 ( )
A. 22 B. 89 C. 92 D. 96
D
模拟演练
2. 花园小区20户家庭的日用电量统计如下表所示:
日用电量/千瓦时
4
5
6
7
8
10
户数
1
3
6
5
4
1
则这20户家庭日用电量的中位数是 ( )
A. 7.5 B. 6 C. 7 D. 6.5
D
典型例题
新知2:众数
【例3】某同学一周中每天完成家庭作业所花时间(单位:分钟)分别为:35,40,45,40,55,40,48,则这组数据的众数是 ( )
A. 35 B. 40 C. 45 D. 55
B
模拟演练
3. 已知一组数据6,3,x,4,4,5,6的众数是6,则x的值是__________.
6
【例4】九年级某班40位同学的年龄如下表所示:
年龄/岁
13
14
15
16
人数
3
16
19
2
则该班40名同学年龄的众数是__________岁.
15
典型例题
模拟演练
4. 据调查,某班30位同学所穿鞋子的尺码如下表所示(单位:码),则该班这30位同学所穿鞋子尺码的众数是 ( )
D
码号
33
34
35
36
37
人数
3
6
8
8
5
A.8 B.35
C. 36 D. 35和36
新知3:运用众数、中位数、平均数分析数据的集中趋势
【例5】某中学举办了一次以“我的中国梦”为主题的演讲比赛. 最后确定7名同学参加决赛,他们的决赛成绩各不相同,其中李华已经知道自己的成绩,但能否进前四名,他还必须清楚这7名同学成绩的__________(填“平均数”“众数”或“中位数”).
中位数
典型例题
5. 某商场为了统计某品牌运动鞋哪个尺码卖得最好,则应关注该品牌运动鞋各尺码销售数据的平均数、众数、中位数这三个数据中的__________.
模拟演练
众数
【例6】某学习兴趣小组参加一次单元测验,成绩统计情况如下表(单位:分):
分数
73
74
75
76
77
78
79
82
83
84
86
88
90
92
人数
1
1
5
4
3
2
3
1
1
1
2
3
1
2
典型例题
(1)该兴趣小组共有多少人?
(2)兴趣小组本次单元测试成绩的平均数、中位数、众数各是多少?
(3)老师打算为兴趣小组下单元考试设定一个新目标,学生达到或超过目标给予奖励,并希望小组三分之一左右的优秀学生得到奖励.请你帮老师从平均数、中位数、众数三个数中选择一个比较恰当的目标数.如果计划让一半左右的人都得到奖励,确定哪个数作为目标恰当些?
解:(1)该兴趣小组的总人数为1+1+5+4+3+2+3+1+1+1+2+3+1+2=30(人).
(2)本次单元测试成绩的平均数为
×73+74+75×5+76×4+77×3+78×2+79×3+82
+83+84+86×2+88×3+90+92×2)=80.3(分).表格中数据已经按照从小到大的顺序排列,一共有30个数,位于第15,第16的数都是78,所以中位数是(78+78)÷2=78(分).75出现了5次,次数最多,所以众数是75分.
(3)由(2)可知,平均数为80.3分,中位数为78分,众数为75分,如果希望小组三分之一左右的优秀学生得到奖励,老师可以选择平均数.如果计划让一半左右的人都得到奖励,确定中位数作为目标恰当些,因为中位数以上的人数占总人数的一半左右.
6. 某中学数学活动小组为了调查居民的用水情况,从某社区的1 500户家庭中随机抽取了30户家庭的月用水量,结果如下表所示:
模拟演练
月用水量/t
3
4
5
7
8
9
40
户数
4
3
5
11
4
2
1
(1)求这30户家庭月用水量的平均数、众数和中位数;
(2)根据上述数据,试估计该社区的月用水量;
(3)由于我国水资源缺乏,许多城市常利用分段计费的方法引导人们节约用水,即规定每个家庭的月基本用水量为m(t),家庭月用水量不超过m(t)的部分按原价收费,超过m(t)的部分加倍收费. 你认为上述问题中的平均数、众数和中位数中哪一个量作为月基本用水量比较合适?简述理由.
解:(1)这30户家庭月用水量的平均数为
×(3×4+4×3+5×5+7×11+8×4+9×2+ 40×1)=7.2(t).
因为7出现了11次,出现的次数最多,所以众数是7 t.
因为共有30个数,所以中位数是第15,第16个数的平均数,即中位数是(7+7)÷2=7(t).
(2)因为该社区共1 500户家庭,所以该社区的月用水量约为7.2×1 500=10 800(t).
(3)用众数或中位数作为月基本用水量比较合适,因为满足大多数家庭用水量的需求,而抽样的30户家庭的用水量存在较大数据,影响了平均数,故不宜采用平均数.
分层训练
【A组】
1. 在一组数据3,4,4,6,8中,下列说法错误的是
( )
A. 它的众数是4
B. 它的平均数是5
C. 它的中位数是5
D. 它的众数等于中位数
C
2. 某篮球兴趣小组7名学生参加投篮比赛,每人投10个,投中的个数分别为:8,5,7,5,8,6,8,则这组数据的众数和中位数分别为 ( )
A. 5,7 B. 6,7
C. 8,6 D. 8,7
D
3.广州市春季某一周的最高气温统计如下表:
则这组数据的中位数与众数分别是 ( )
A. 27,28 B. 27.5,28
C. 28,27 D. 26.5,27
最高气温/℃
25
26
27
28
天数
1
1
2
3
A
4. 已知数据x1,x2,x3,x4,…,xn的平均数是m,中位数是n,众数是t,则数据3x1+7,3x2+7,3x3+7,…,3xn+7的平均数是__________,中位数是__________,众数是__________.
3m+7
3n+7
3t+7
【B组】
5. 小强在最近的5场篮球赛中,得分分别为10,13,9,8,10分. 若小强下一场球赛得分是16分,则小强得分的平均数、中位数和众数中,发生改变的是__________.
平均数
6. 某服装店为调动营业员的积极性,决定实行目标管理,根据每月销售目标完成情况发放奖金. 该店统计了每位营业员前半年的月均销售额,并算出所得数据的平均数、众数、中位数,分别为22,15,18(单位:万元). 若想让一半左右的营业员都能达到月销售目标,则月销售额定为__________万元较为合适.
18
7. 某鞋店一周内销售了某种品牌的男鞋60双,各种尺码的销量统计如下:
由此你能给这家鞋店提供的进货建议是__________
_____________________________________________.
尺码/cm
23.5
24
24.5
25
25.5
26
26.5
销量/双
3
7
6
18
18
7
2
25 cm和
25.5 cm尺码的鞋子多进一些(合理即可)
【C组】
8. 甲、乙、丙三个家电厂家在广告中都声称,他们的某种电子产品在正常情况下的使用寿命都是8年,经质量检测部门对这三家销售的产品的使用寿命进行跟踪调查,统计结果如下(单位:年).
甲厂:4,5,5,5,5,7,9,12,13,15;
乙厂:6,6,8,8,8,9,10,12,14,15;
丙厂:4,4,4,6,7,9,13,15,16,16.
请回答下列问题.
(1)填空:
(2)这三个厂家的销售广告分别利用了哪一种数据表示集中趋势的特征数?
(3)如果你是顾客,你会买三家中哪一家的电子产品?为什么?
厂家
平均数
众数
中位数
甲厂
________
_______
6
乙厂
9.6
________
8.5
丙厂
9.4
4
_______
解:(1)
厂家
平均数
众数
中位数
甲厂
________
_______
6
乙厂
9.6
________
8.5
丙厂
9.4
4
_______
8
5
8
8
(2)甲厂家的销售广告利用了平均数“8”表示集中趋势的特征数;
乙厂家的销售广告利用了众数“8”表示集中趋势的特征数;
丙厂家的销售广告利用了中位数“8”表示集中趋势的特征数.
(3)通过(1)中表格可知平均数为乙>丙>甲;众数为乙>甲>丙;中位数为乙>丙>甲.
顾客在选购产品时,一般以平均数为依据,选平均数大的厂家的产品,因此应选乙厂家的产品.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
