北师大版数学八年级上册7.3 平行线的判定习题课件(26张)
文档属性
| 名称 | 北师大版数学八年级上册7.3 平行线的判定习题课件(26张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-25 14:08:49 | ||
图片预览





文档简介
名师导学
A. (1)判定定理1:同位角__________,两直线平行;
(2)判定定理2:内错角__________,两直线平行.
(3)判定定理3:同旁内角__________,两直线平行.
相等
相等
互补
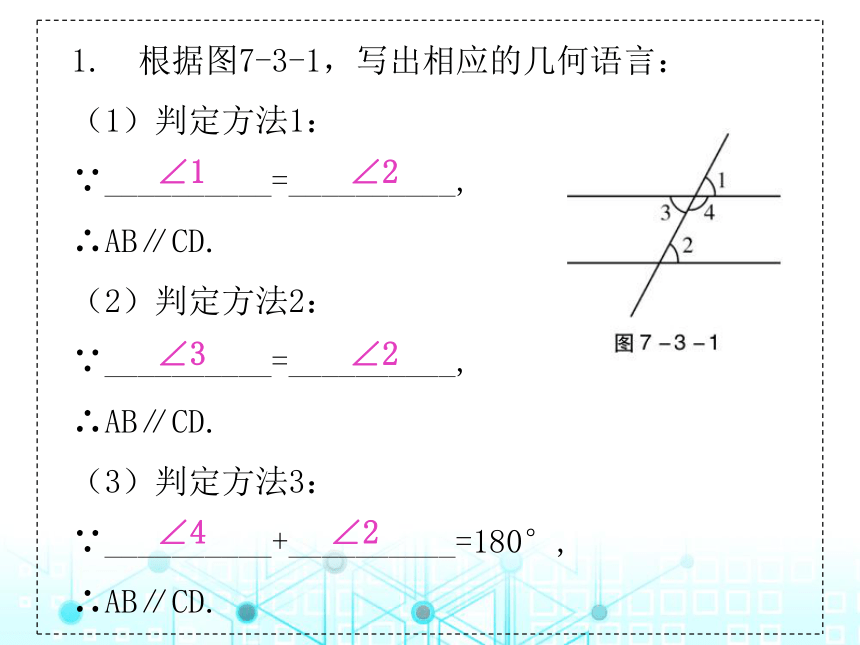
1. 根据图7-3-1,写出相应的几何语言:
(1)判定方法1:
∵__________=__________,
∴AB∥CD.
(2)判定方法2:
∵__________=__________,
∴AB∥CD.
(3)判定方法3:
∵__________+__________=180°,
∴AB∥CD.
∠1
∠2
∠3
∠2
∠4
∠2
课堂讲练
典型例题
新知1:同位角相等,两直线平行
【例1】如图7-3-2,已知∠1=∠2. 求证:a∥b. 证明:∵∠1=∠2(已知),
∠2=∠3(______________),
∴∠1=________(______________).
∴a∥b(________________________).
对顶角相等
∠3
等量代换
同位角相等,两直线平行
模拟演练
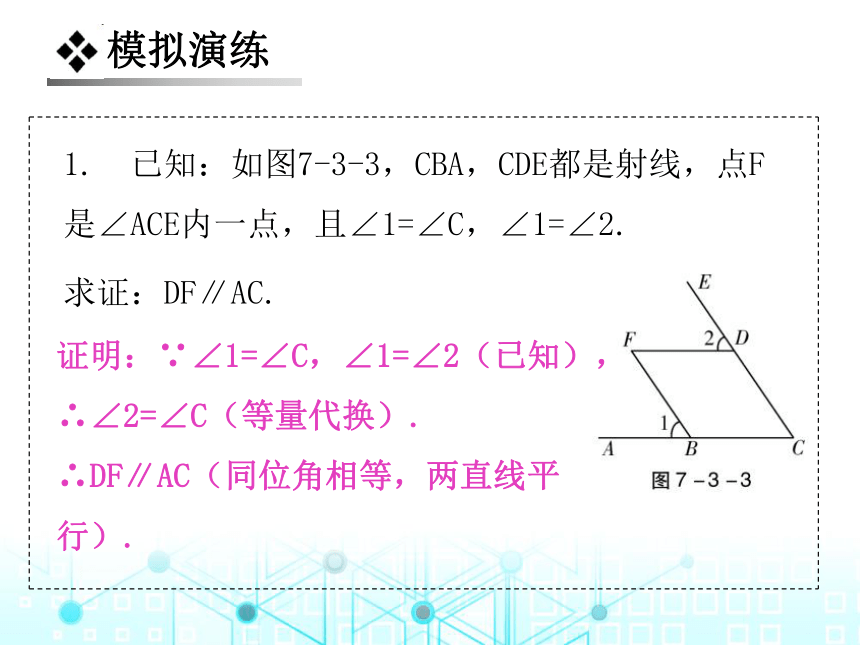
1. 已知:如图7-3-3,CBA,CDE都是射线,点F是∠ACE内一点,且∠1=∠C,∠1=∠2.
求证:DF∥AC.
证明:∵∠1=∠C,∠1=∠2(已知),
∴∠2=∠C(等量代换).
∴DF∥AC(同位角相等,两直线平行).
新知2:内错角相等,两直线平行
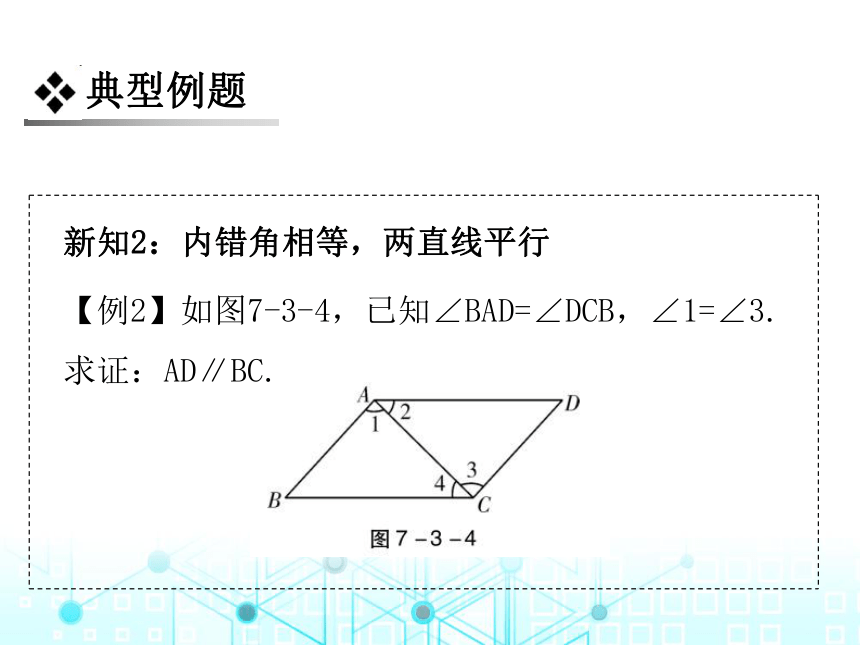
【例2】如图7-3-4,已知∠BAD=∠DCB,∠1=∠3. 求证:AD∥BC.
典型例题
证明:∵∠BAD=∠DCB,∠1=∠3(__________),∴∠BAD-__________=∠DCB-__________(等式的性质),即__________=__________.
∴AD∥BC(_______________________________).
已知
∠1
∠3
∠2
∠4
内错角相等,两直线平行
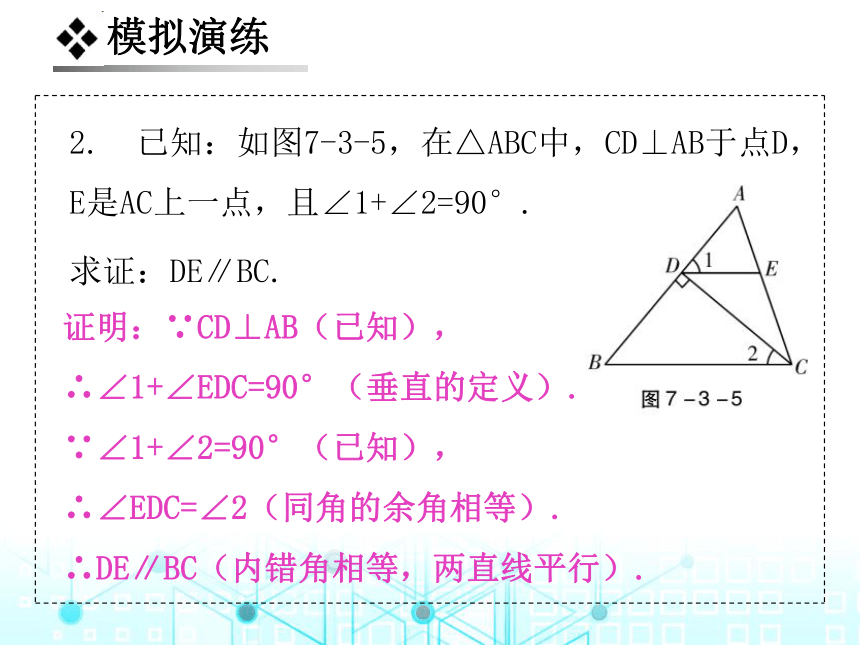
2. 已知:如图7-3-5,在△ABC中,CD⊥AB于点D,E是AC上一点,且∠1+∠2=90°.
求证:DE∥BC.
证明:∵CD⊥AB(已知),
∴∠1+∠EDC=90°(垂直的定义).
∵∠1+∠2=90°(已知),
∴∠EDC=∠2(同角的余角相等).
∴DE∥BC(内错角相等,两直线平行).
模拟演练
新知3:同旁内角互补,两直线平行
【例3】如图7-3-6,已知∠1=110°,∠2=70°. 求证:a∥b.
证明:∵∠1=110°(已知),∠3=∠1(______________),
∴∠3=110°(_____________).
又∵__________(已知),
∴∠2+∠3=180°(平角的定义).
∴a∥b(____________________________).
对顶角相等
等量代换
∠2=70°
同旁内角互补,两直线平行
典型例题
模拟演练
3. 如图7-3-7,一个弯形管道ABCD的拐角∠ABC=115°,∠BCD=65°,这时管道所在的直线AB,CD平行吗?说明理由.
解:AB与CD平行.
理由如下.
∵∠ABC=115°,∠BCD=65°(已知),
∴∠ABC+∠BCD=180°(平角的定义).
∴AB∥CD(同旁内角互补,两直线平行).
分层训练
【A组】
1.如图7-3-8,∠1=∠2,下列结论正确的是
( )
A. AB∥CD B. AD∥BC
C. AD∥EF D. EF∥BC
C
2.如图7-3-9,下列条件能够判断EG∥HC的是
( )
A. ∠FEB=∠ECD
B. ∠AEG=∠DCH
C. ∠GEC=∠HCF
D. ∠CEB+∠ECD=180°
C
3. 如图7-3-10,在四边形ABCD中,点E在BC上,连接DE. 下列说法正确的是 ( )
A. 因为∠A=∠B,所以AD∥BC
B. 因为∠B=∠EDC,所以AB∥DE
C. 因为∠B+∠DEB=180°,所以AB∥DE
D. 因为∠B=∠DEC,所以AD∥BC
C
4. 如图7-3-11,下列条件能判断AB∥CD的是
( )
A. ∠FEC=∠EFB
B. ∠BFC+∠C=180°
C. ∠BEF=∠EFC
D. ∠C=∠BFD
C
5. 如图7-3-12,下列条件不能判断直线a∥b的是
( )
A. ∠1+∠3=180°
B. ∠2=∠3
C. ∠4=∠5
D. ∠4=∠6
C
6. 平面上五条直线l1,l2,l3,l4和l5相交的情形如图7-3-13,根据图中标出的角度,下列叙述正确的是 ( )
A. l1和l3不平行,l2和l3平行
B. l1和l3不平行,l2和l3不平行
C. l1和l3平行,l2和l3平行
D. l1和l3平行,l2和l3不平行
A
【B组】
7. 如图7-3-14,下列条件:①∠1=∠2,②∠3+∠4=180°,③∠5+∠6=180°,④∠2=∠3中,能判断直线a∥b的有 ( )
A. 1个
B. 2个
C. 3个
D. 4个
C
8. 如图7-3-15,已知直线EF⊥MN,垂足为点F,且∠1=140°,则当∠2等于__________时,AB∥CD.
50°
9. 已知:如图7-3-16,∠ABC=∠ADC,BF和DE分别平分∠ABC和∠ADC,∠AED=∠EDC.
求证:ED∥BF.
证明:∵BF和DE分别平分∠ABC和∠ADC(已知),
∴∠EDC=__________∠ADC,
∠FBA=__________∠ABC(角平分线的定义).
∵∠ADC=∠ABC(已知),
∴∠__________=∠FBA(等量代换).
∵∠AED=∠EDC(已知),
∴∠__________=∠__________(等量代换).
∴ED∥BF(_______________________________).
12
12
EDC
FBA
AED
同位角相等,两直线平行
10. 如图7-3-17,CD平分∠ECF,∠B=∠ACB.
求证:AB∥CE.
证明:∵CD平分∠ECF(已知),
∴∠ECD=∠DCF(角平分线的定义).
∵∠ACB=∠DCF(对顶角相等),
∴∠ECD=∠ACB(等量代换).
又∵∠B=∠ACB(已知),
∴∠B=∠ECD(等量代换).
∴AB∥CE(同位角相等,两直线平行).
【C组】
11. 如图7-3-18,已知CE⊥DG,垂足为点C,∠BAF=50°,∠ACE=140°.
求证:AB∥CD.
证明:∵CE⊥DG(已知),
∴∠ECG=90°(垂直的定义).
∵∠ACE=140°(已知),
∴∠ACG=∠ACE-∠ECG=50°(等式的性质).
∵∠BAF=50°(已知),
∴∠BAF=∠ACG(等量代换).
∴AB∥CD(同位角相等,两直线平行).
12. 如图7-3-19,直线a,b被直线c所截,∠1+∠2=180°,试用三种方法证明a∥b.
证明:(方法一)
∵∠1+∠2=180°(已知),
∠2+∠5=180°(平角的定义),
∴∠1=∠5(等量代换).
∴a∥b(同位角相等,两直线平行).
(方法二)∵∠1+∠2=180°(已知),
∠1=∠3(对顶角相等),
∴∠2+∠3=180°(等量代换).
∴a∥b(同旁内角互补,两直线平行).
(方法三)∵∠1+∠2=180°(已知),
∠2+∠5=180°(平角的定义),
∠1=∠3(对顶角相等),
∴∠1=∠5=∠3(等量代换).
∴a∥b(内错角相等,两直线平行).
A. (1)判定定理1:同位角__________,两直线平行;
(2)判定定理2:内错角__________,两直线平行.
(3)判定定理3:同旁内角__________,两直线平行.
相等
相等
互补
1. 根据图7-3-1,写出相应的几何语言:
(1)判定方法1:
∵__________=__________,
∴AB∥CD.
(2)判定方法2:
∵__________=__________,
∴AB∥CD.
(3)判定方法3:
∵__________+__________=180°,
∴AB∥CD.
∠1
∠2
∠3
∠2
∠4
∠2
课堂讲练
典型例题
新知1:同位角相等,两直线平行
【例1】如图7-3-2,已知∠1=∠2. 求证:a∥b. 证明:∵∠1=∠2(已知),
∠2=∠3(______________),
∴∠1=________(______________).
∴a∥b(________________________).
对顶角相等
∠3
等量代换
同位角相等,两直线平行
模拟演练
1. 已知:如图7-3-3,CBA,CDE都是射线,点F是∠ACE内一点,且∠1=∠C,∠1=∠2.
求证:DF∥AC.
证明:∵∠1=∠C,∠1=∠2(已知),
∴∠2=∠C(等量代换).
∴DF∥AC(同位角相等,两直线平行).
新知2:内错角相等,两直线平行
【例2】如图7-3-4,已知∠BAD=∠DCB,∠1=∠3. 求证:AD∥BC.
典型例题
证明:∵∠BAD=∠DCB,∠1=∠3(__________),∴∠BAD-__________=∠DCB-__________(等式的性质),即__________=__________.
∴AD∥BC(_______________________________).
已知
∠1
∠3
∠2
∠4
内错角相等,两直线平行
2. 已知:如图7-3-5,在△ABC中,CD⊥AB于点D,E是AC上一点,且∠1+∠2=90°.
求证:DE∥BC.
证明:∵CD⊥AB(已知),
∴∠1+∠EDC=90°(垂直的定义).
∵∠1+∠2=90°(已知),
∴∠EDC=∠2(同角的余角相等).
∴DE∥BC(内错角相等,两直线平行).
模拟演练
新知3:同旁内角互补,两直线平行
【例3】如图7-3-6,已知∠1=110°,∠2=70°. 求证:a∥b.
证明:∵∠1=110°(已知),∠3=∠1(______________),
∴∠3=110°(_____________).
又∵__________(已知),
∴∠2+∠3=180°(平角的定义).
∴a∥b(____________________________).
对顶角相等
等量代换
∠2=70°
同旁内角互补,两直线平行
典型例题
模拟演练
3. 如图7-3-7,一个弯形管道ABCD的拐角∠ABC=115°,∠BCD=65°,这时管道所在的直线AB,CD平行吗?说明理由.
解:AB与CD平行.
理由如下.
∵∠ABC=115°,∠BCD=65°(已知),
∴∠ABC+∠BCD=180°(平角的定义).
∴AB∥CD(同旁内角互补,两直线平行).
分层训练
【A组】
1.如图7-3-8,∠1=∠2,下列结论正确的是
( )
A. AB∥CD B. AD∥BC
C. AD∥EF D. EF∥BC
C
2.如图7-3-9,下列条件能够判断EG∥HC的是
( )
A. ∠FEB=∠ECD
B. ∠AEG=∠DCH
C. ∠GEC=∠HCF
D. ∠CEB+∠ECD=180°
C
3. 如图7-3-10,在四边形ABCD中,点E在BC上,连接DE. 下列说法正确的是 ( )
A. 因为∠A=∠B,所以AD∥BC
B. 因为∠B=∠EDC,所以AB∥DE
C. 因为∠B+∠DEB=180°,所以AB∥DE
D. 因为∠B=∠DEC,所以AD∥BC
C
4. 如图7-3-11,下列条件能判断AB∥CD的是
( )
A. ∠FEC=∠EFB
B. ∠BFC+∠C=180°
C. ∠BEF=∠EFC
D. ∠C=∠BFD
C
5. 如图7-3-12,下列条件不能判断直线a∥b的是
( )
A. ∠1+∠3=180°
B. ∠2=∠3
C. ∠4=∠5
D. ∠4=∠6
C
6. 平面上五条直线l1,l2,l3,l4和l5相交的情形如图7-3-13,根据图中标出的角度,下列叙述正确的是 ( )
A. l1和l3不平行,l2和l3平行
B. l1和l3不平行,l2和l3不平行
C. l1和l3平行,l2和l3平行
D. l1和l3平行,l2和l3不平行
A
【B组】
7. 如图7-3-14,下列条件:①∠1=∠2,②∠3+∠4=180°,③∠5+∠6=180°,④∠2=∠3中,能判断直线a∥b的有 ( )
A. 1个
B. 2个
C. 3个
D. 4个
C
8. 如图7-3-15,已知直线EF⊥MN,垂足为点F,且∠1=140°,则当∠2等于__________时,AB∥CD.
50°
9. 已知:如图7-3-16,∠ABC=∠ADC,BF和DE分别平分∠ABC和∠ADC,∠AED=∠EDC.
求证:ED∥BF.
证明:∵BF和DE分别平分∠ABC和∠ADC(已知),
∴∠EDC=__________∠ADC,
∠FBA=__________∠ABC(角平分线的定义).
∵∠ADC=∠ABC(已知),
∴∠__________=∠FBA(等量代换).
∵∠AED=∠EDC(已知),
∴∠__________=∠__________(等量代换).
∴ED∥BF(_______________________________).
12
12
EDC
FBA
AED
同位角相等,两直线平行
10. 如图7-3-17,CD平分∠ECF,∠B=∠ACB.
求证:AB∥CE.
证明:∵CD平分∠ECF(已知),
∴∠ECD=∠DCF(角平分线的定义).
∵∠ACB=∠DCF(对顶角相等),
∴∠ECD=∠ACB(等量代换).
又∵∠B=∠ACB(已知),
∴∠B=∠ECD(等量代换).
∴AB∥CE(同位角相等,两直线平行).
【C组】
11. 如图7-3-18,已知CE⊥DG,垂足为点C,∠BAF=50°,∠ACE=140°.
求证:AB∥CD.
证明:∵CE⊥DG(已知),
∴∠ECG=90°(垂直的定义).
∵∠ACE=140°(已知),
∴∠ACG=∠ACE-∠ECG=50°(等式的性质).
∵∠BAF=50°(已知),
∴∠BAF=∠ACG(等量代换).
∴AB∥CD(同位角相等,两直线平行).
12. 如图7-3-19,直线a,b被直线c所截,∠1+∠2=180°,试用三种方法证明a∥b.
证明:(方法一)
∵∠1+∠2=180°(已知),
∠2+∠5=180°(平角的定义),
∴∠1=∠5(等量代换).
∴a∥b(同位角相等,两直线平行).
(方法二)∵∠1+∠2=180°(已知),
∠1=∠3(对顶角相等),
∴∠2+∠3=180°(等量代换).
∴a∥b(同旁内角互补,两直线平行).
(方法三)∵∠1+∠2=180°(已知),
∠2+∠5=180°(平角的定义),
∠1=∠3(对顶角相等),
∴∠1=∠5=∠3(等量代换).
∴a∥b(内错角相等,两直线平行).
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
