北师大版数学七年级上册第五章 一元一次方程 达标检测卷(word版含答案)
文档属性
| 名称 | 北师大版数学七年级上册第五章 一元一次方程 达标检测卷(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 443.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-25 15:19:50 | ||
图片预览


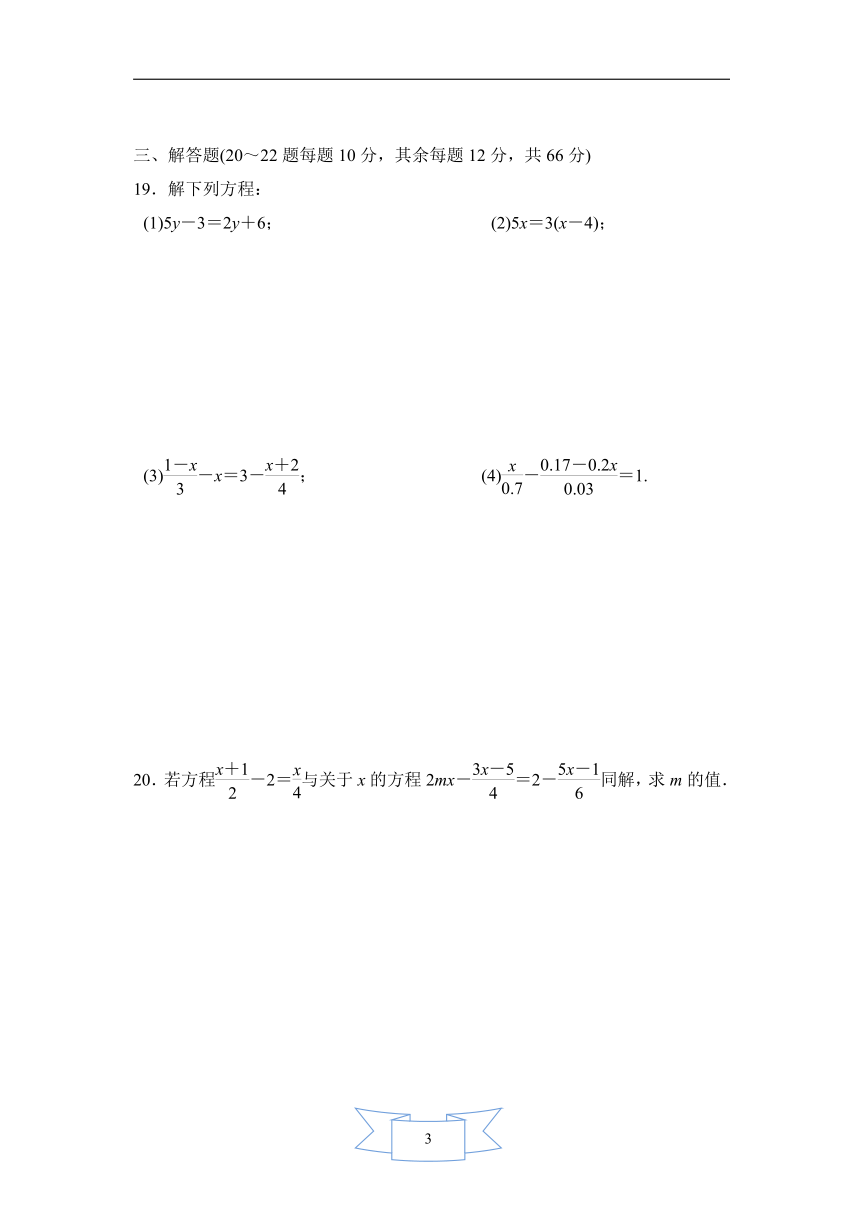

文档简介
第五章达标检测卷
一、选择题(每题3分,共30分)
1.下列等式是一元一次方程的是( )
A.x-2=3 B.1+5=6
C.x2+x=1 D.x-3y=0
2.下列等式变形正确的是( )
A.若a=b,则a-3=3-b B.若x=y,则=
C.若a=b,则ac=bc D.若=,则b=d
3.方程2x-3=7的解是( )
A.x=5 B.x=4 C.x=3.5 D.x=2
4.将方程+1=去分母后正确的是( )
A.3(x+2)+1=4x B.12(x+2)+12=12x
C.4(x+2)+12=3x D.3(x+2)+12=4x
5.若2(a+3)的值与4互为相反数,则a的值为( )
A.-1 B.- C.-5 D.
6.若x=-3是方程2(x-m)=6的解,则m的值为( )
A.6 B.-6 C.12 D.-12
7.已知方程7x+2=3x-6与关于x的方程x-1=k的解相同,则3k2-1的值为( )
A.18 B.20 C.26 D.-26
8.甲、乙两人练习赛跑,甲每秒跑7 m,乙每秒跑6.5 m,甲让乙先跑5 m,设甲跑x s后可追上乙,则下列四个方程中不正确的是( )
A.7x=6.5x+5 B.7x+5=6.5x
C.(7-6.5)x=5 D.6.5x=7x-5
9.小马虎在做作业,不小心将方程中的一个常数污染了,被污染的方程是2(x-3)-■=x+1,怎么办呢?他想了想便翻看书后的答案,方程的解是x=9,请问这个被污染的常数是( )
A.1 B.2 C.3 D.4
10.有m辆客车及n人,若每辆客车乘40人,则还有10人不能上车;若每辆客车乘43人,则只有1人不能上车.有下列四个等式:①40m+10=43m-1;②=;③=;④40m+10=43m+1.其中正确的是( )
A.①② B.②④ C.②③ D.③④
二、填空题(每题3分,共24分)
11.方程(m+1)x|m|-2=1是关于x的一元一次方程,则m=________.
12.已知x-2y+3=0,则代数式-2x+4y+2 021的值为________.
13.若3x3ym-1与-xn+2y4是同类项,则m+n=________.
14.美术馆举办的一次画展中,展出的油画作品和国画作品共有100幅,其中油画作品数量比国画作品数量的2倍多7幅,则展出的油画作品有_____幅.
15.一个两位数,个位上的数字是十位上的数字的2倍,如果把十位上与个位上的数字对调,那么所得的两位数比原两位数大27,求原两位数.若设原两位数个位上的数字为x,则可列方程为____________________;若设原两位数十位上的数字为y,则可列方程为______________________.
16.甲、乙两个足球队连续进行对抗赛,规定胜一场得3分,平一场得1分,负一场得0分,共赛10场,甲队保持不败,得22分,甲队胜________场.
17. 一台空调标价2 000元,若按六折销售仍可获利20%,则这台空调的进价是________元.
18.如图,两根铁棒直立于桶底水平的木桶中,在木桶中加入水后,一根露出水面的长度是它的,另一根露出水面的长度是它的,两根铁棒长度之和为55 cm,此时木桶中水的深度是________.
三、解答题(20~22题每题10分,其余每题12分,共66分)
19.解下列方程:
(1)5y-3=2y+6; (2)5x=3(x-4);
(3)-x=3-; (4)-=1.
20.若方程-2=与关于x的方程2mx-=2-同解,求m的值.
21.下面是小红解方程-=1的过程.
解:去分母,得2(2x+1)-5x-1=1.①
去括号,得4x+2-5x-1=1.②
移项,得4x-5x=1-2+1.③
合并同类项,得-x=0.④
系数化为1,得x=0.⑤
上述解方程的过程中,是否有错误?
答:________(填“有”或者“没有”);如果有错误,则开始出错的一步是________(填序号).如果上述解方程有错误,请你给出正确的解题过程.
22.某市为更有效地利用水资源,制定了居民用水收费标准:如果一户每月用水量不超过15 m3,按每立方米1.8元收费;如果超过15 m3,超过部分按每立方米2.3元收费,其余仍按每立方米1.8元收费.另外,每立方米加收污水处理费1元.若某户1月共支付水费58.5元,求该户1月的用水量.
23.微商琪琪计划购进A,B两款果汁机共12台在朋友圈进行销售,这两款果汁机的进价、售价如下表:
进价/(元/台) 售价/(元/台)
A款 250 350
B款 450 600
(1)如何进货才能使进货款恰好为4 000元?
(2)如何进货才能使销售完这批果汁机时获得的利润恰好为1 550元?
24.某市居民生活用电基本价格为每千瓦时0.60元,若每月用电量超过a kW·h,超出部分按基本电价的120%收费.
(1)某用户6月用电150 kW·h,共交电费93.6元,求a的值.
(2)若该用户7月的电费平均每千瓦时为0.66元,则7月用电多少千瓦时?应交电费多少元?
答案
一、1.A 2.C 3.A 4.D 5.C 6.B
7.C 8.B 9.B 10.D
二、11.1 12.2 027
13.6 点拨:由题意得m-1=4,n+2=3,解得m=5,n=1.所以m+n=6.
14.69
15.10×+x=10x+-27;
10y+2y=10×2y+y-27
16.6 17.1 000 18.20 cm
三、19.解:(1)移项,得5y-2y=6+3.
合并同类项,得3y=9.
系数化为1,得y=3.
(2)去括号,得5x=3x-12.
移项,得5x-3x=-12.
合并同类项,得2x=-12.
系数化为1,得x=-6.
(3)去分母,得4(1-x)-12x=36-3(x+2).
去括号,得4-4x-12x=36-3x-6.
移项,得3x-4x-12x=36-6-4.
合并同类项,得-13x=26.
系数化为1,得x=-2.
(4)原方程可化为-=1.
去分母,得30x-7(17-20x)=21.
去括号,得30x-119+140x=21.
移项、合并同类项,得170x=140.
系数化为1,得x=.
20.解:解方程-2=,得x=6,
将x=6代入2mx-=2-,
得12m-=2-,
解得m=.
21.解:有;①
正确的解题过程:
去分母,得2(2x+1)-(5x-1)=6.
去括号,得4x+2-5x+1=6.
移项,得4x-5x=6-2-1.
合并同类项,得-x=3.
系数化为1,得x=-3.
22.解:若该户1月的用水量为15 m3,则需支付水费15×(1.8+1)=42(元),而42<58.5,所以该户1月的用水量超过15 m3.
设该户1月的用水量为x m3,则列方程为42+(2.3+1)(x-15)=58.5,解得x=20.
答:该户1月的用水量为20 m3.
23.解:(1)设微商琪琪购进A款果汁机x台,则购进B款果汁机(12-x)台,
由题意,得250x+450(12-x)=4 000,
解得x=7.
12-7=5(台),
答:微商琪琪购进A款果汁机7台,B款果汁机5台,才能使进货款恰好为4 000元.
(2)设微商琪琪购进A款果汁机a台,则购进B款果汁机(12-a)台,
由题意,得(350-250)a+(600-450)(12-a)=1 550.
解得a=5.
12-5=7(台),
答:微商琪琪购进A款果汁机5台,B款果汁机7台,才能使销售完这批果汁机时获得的利润恰好为1 550元.
24.解:(1)因为0.60×150=90(元)<93.6元,所以a<150.
由题意,得0.60a+(150-a)×0.60×120%=93.6,
解得a=120.
(2)设7月用电x kW·h.
由题意,得0.66x=0.60×120+0.60×(x-120)×120%,解得x=240.
所以0.66x=0.66×240=158.4.
答:7月用电240 kW·h,应交电费158.4元.
一、选择题(每题3分,共30分)
1.下列等式是一元一次方程的是( )
A.x-2=3 B.1+5=6
C.x2+x=1 D.x-3y=0
2.下列等式变形正确的是( )
A.若a=b,则a-3=3-b B.若x=y,则=
C.若a=b,则ac=bc D.若=,则b=d
3.方程2x-3=7的解是( )
A.x=5 B.x=4 C.x=3.5 D.x=2
4.将方程+1=去分母后正确的是( )
A.3(x+2)+1=4x B.12(x+2)+12=12x
C.4(x+2)+12=3x D.3(x+2)+12=4x
5.若2(a+3)的值与4互为相反数,则a的值为( )
A.-1 B.- C.-5 D.
6.若x=-3是方程2(x-m)=6的解,则m的值为( )
A.6 B.-6 C.12 D.-12
7.已知方程7x+2=3x-6与关于x的方程x-1=k的解相同,则3k2-1的值为( )
A.18 B.20 C.26 D.-26
8.甲、乙两人练习赛跑,甲每秒跑7 m,乙每秒跑6.5 m,甲让乙先跑5 m,设甲跑x s后可追上乙,则下列四个方程中不正确的是( )
A.7x=6.5x+5 B.7x+5=6.5x
C.(7-6.5)x=5 D.6.5x=7x-5
9.小马虎在做作业,不小心将方程中的一个常数污染了,被污染的方程是2(x-3)-■=x+1,怎么办呢?他想了想便翻看书后的答案,方程的解是x=9,请问这个被污染的常数是( )
A.1 B.2 C.3 D.4
10.有m辆客车及n人,若每辆客车乘40人,则还有10人不能上车;若每辆客车乘43人,则只有1人不能上车.有下列四个等式:①40m+10=43m-1;②=;③=;④40m+10=43m+1.其中正确的是( )
A.①② B.②④ C.②③ D.③④
二、填空题(每题3分,共24分)
11.方程(m+1)x|m|-2=1是关于x的一元一次方程,则m=________.
12.已知x-2y+3=0,则代数式-2x+4y+2 021的值为________.
13.若3x3ym-1与-xn+2y4是同类项,则m+n=________.
14.美术馆举办的一次画展中,展出的油画作品和国画作品共有100幅,其中油画作品数量比国画作品数量的2倍多7幅,则展出的油画作品有_____幅.
15.一个两位数,个位上的数字是十位上的数字的2倍,如果把十位上与个位上的数字对调,那么所得的两位数比原两位数大27,求原两位数.若设原两位数个位上的数字为x,则可列方程为____________________;若设原两位数十位上的数字为y,则可列方程为______________________.
16.甲、乙两个足球队连续进行对抗赛,规定胜一场得3分,平一场得1分,负一场得0分,共赛10场,甲队保持不败,得22分,甲队胜________场.
17. 一台空调标价2 000元,若按六折销售仍可获利20%,则这台空调的进价是________元.
18.如图,两根铁棒直立于桶底水平的木桶中,在木桶中加入水后,一根露出水面的长度是它的,另一根露出水面的长度是它的,两根铁棒长度之和为55 cm,此时木桶中水的深度是________.
三、解答题(20~22题每题10分,其余每题12分,共66分)
19.解下列方程:
(1)5y-3=2y+6; (2)5x=3(x-4);
(3)-x=3-; (4)-=1.
20.若方程-2=与关于x的方程2mx-=2-同解,求m的值.
21.下面是小红解方程-=1的过程.
解:去分母,得2(2x+1)-5x-1=1.①
去括号,得4x+2-5x-1=1.②
移项,得4x-5x=1-2+1.③
合并同类项,得-x=0.④
系数化为1,得x=0.⑤
上述解方程的过程中,是否有错误?
答:________(填“有”或者“没有”);如果有错误,则开始出错的一步是________(填序号).如果上述解方程有错误,请你给出正确的解题过程.
22.某市为更有效地利用水资源,制定了居民用水收费标准:如果一户每月用水量不超过15 m3,按每立方米1.8元收费;如果超过15 m3,超过部分按每立方米2.3元收费,其余仍按每立方米1.8元收费.另外,每立方米加收污水处理费1元.若某户1月共支付水费58.5元,求该户1月的用水量.
23.微商琪琪计划购进A,B两款果汁机共12台在朋友圈进行销售,这两款果汁机的进价、售价如下表:
进价/(元/台) 售价/(元/台)
A款 250 350
B款 450 600
(1)如何进货才能使进货款恰好为4 000元?
(2)如何进货才能使销售完这批果汁机时获得的利润恰好为1 550元?
24.某市居民生活用电基本价格为每千瓦时0.60元,若每月用电量超过a kW·h,超出部分按基本电价的120%收费.
(1)某用户6月用电150 kW·h,共交电费93.6元,求a的值.
(2)若该用户7月的电费平均每千瓦时为0.66元,则7月用电多少千瓦时?应交电费多少元?
答案
一、1.A 2.C 3.A 4.D 5.C 6.B
7.C 8.B 9.B 10.D
二、11.1 12.2 027
13.6 点拨:由题意得m-1=4,n+2=3,解得m=5,n=1.所以m+n=6.
14.69
15.10×+x=10x+-27;
10y+2y=10×2y+y-27
16.6 17.1 000 18.20 cm
三、19.解:(1)移项,得5y-2y=6+3.
合并同类项,得3y=9.
系数化为1,得y=3.
(2)去括号,得5x=3x-12.
移项,得5x-3x=-12.
合并同类项,得2x=-12.
系数化为1,得x=-6.
(3)去分母,得4(1-x)-12x=36-3(x+2).
去括号,得4-4x-12x=36-3x-6.
移项,得3x-4x-12x=36-6-4.
合并同类项,得-13x=26.
系数化为1,得x=-2.
(4)原方程可化为-=1.
去分母,得30x-7(17-20x)=21.
去括号,得30x-119+140x=21.
移项、合并同类项,得170x=140.
系数化为1,得x=.
20.解:解方程-2=,得x=6,
将x=6代入2mx-=2-,
得12m-=2-,
解得m=.
21.解:有;①
正确的解题过程:
去分母,得2(2x+1)-(5x-1)=6.
去括号,得4x+2-5x+1=6.
移项,得4x-5x=6-2-1.
合并同类项,得-x=3.
系数化为1,得x=-3.
22.解:若该户1月的用水量为15 m3,则需支付水费15×(1.8+1)=42(元),而42<58.5,所以该户1月的用水量超过15 m3.
设该户1月的用水量为x m3,则列方程为42+(2.3+1)(x-15)=58.5,解得x=20.
答:该户1月的用水量为20 m3.
23.解:(1)设微商琪琪购进A款果汁机x台,则购进B款果汁机(12-x)台,
由题意,得250x+450(12-x)=4 000,
解得x=7.
12-7=5(台),
答:微商琪琪购进A款果汁机7台,B款果汁机5台,才能使进货款恰好为4 000元.
(2)设微商琪琪购进A款果汁机a台,则购进B款果汁机(12-a)台,
由题意,得(350-250)a+(600-450)(12-a)=1 550.
解得a=5.
12-5=7(台),
答:微商琪琪购进A款果汁机5台,B款果汁机7台,才能使销售完这批果汁机时获得的利润恰好为1 550元.
24.解:(1)因为0.60×150=90(元)<93.6元,所以a<150.
由题意,得0.60a+(150-a)×0.60×120%=93.6,
解得a=120.
(2)设7月用电x kW·h.
由题意,得0.66x=0.60×120+0.60×(x-120)×120%,解得x=240.
所以0.66x=0.66×240=158.4.
答:7月用电240 kW·h,应交电费158.4元.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
