人教版数学八年级上册11.2.1三角形的内角1课件(共20张)
文档属性
| 名称 | 人教版数学八年级上册11.2.1三角形的内角1课件(共20张) |  | |
| 格式 | ppt | ||
| 文件大小 | 455.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-26 21:53:17 | ||
图片预览






文档简介
1、掌握三角形的内角和定理并能利用其解决实际问题。
2、明确一个完整的证明题是由哪些部分组成;提高学生用数学语言叙述问题的意识和能力。
3、经历添加辅助线的过程,帮助学生树立解题遇到困难时添加辅助线的意识。
4、经历动手实验得到结论,激发学生学习数学的兴趣。
揭示目标:
预习检测:
1、三角形的内角和定理:
三角形三个内角的和是180 °
即:如图:在△ABC中,
∠A +∠B +∠C=180 °
A
B
C
三角形的三个内角和是多少?如何用数学语言叙述这个定理
把三个角拼在一起试试看?
从刚才拼角的过程你能想出证明的办法吗?
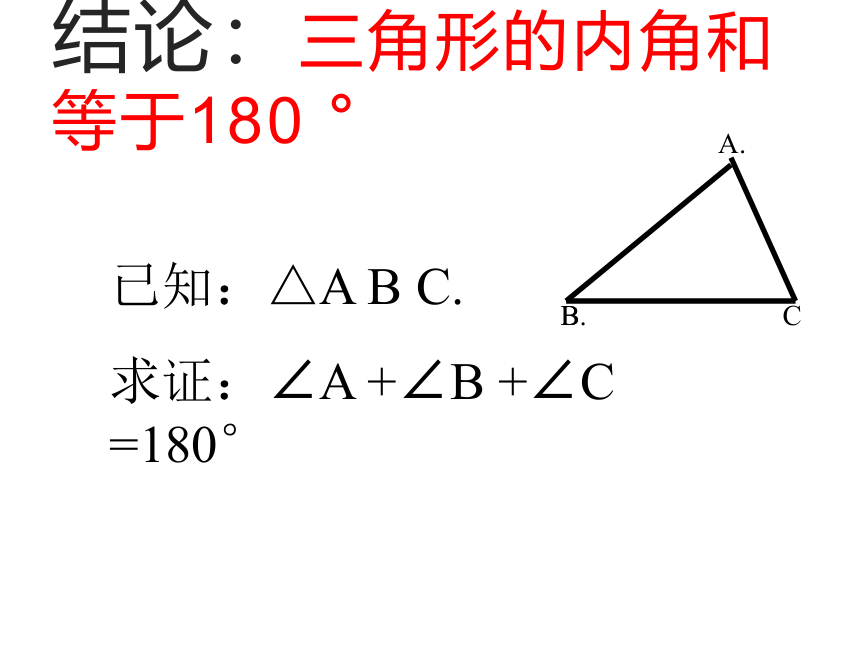
结论:三角形的内角和等于180 °
已知:△A B C.
求证:∠A +∠B +∠C =180°
A.
B
C
B.
E
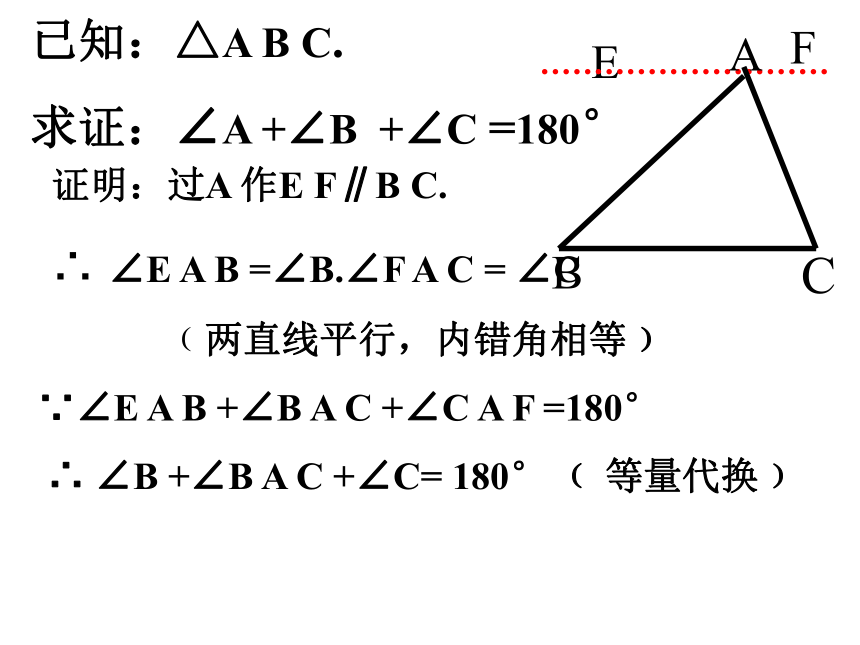
证明:过A 作E F∥B C.
∴ ∠E A B =∠B.∠F A C = ∠C
﹙两直线平行,内错角相等﹚
∵∠E A B +∠B A C +∠C A F =180°
∴ ∠B +∠B A C +∠C= 180° ﹙ 等量代换﹚
F
已知:△A B C.
求证:∠A +∠B +∠C =180°
A
B
C
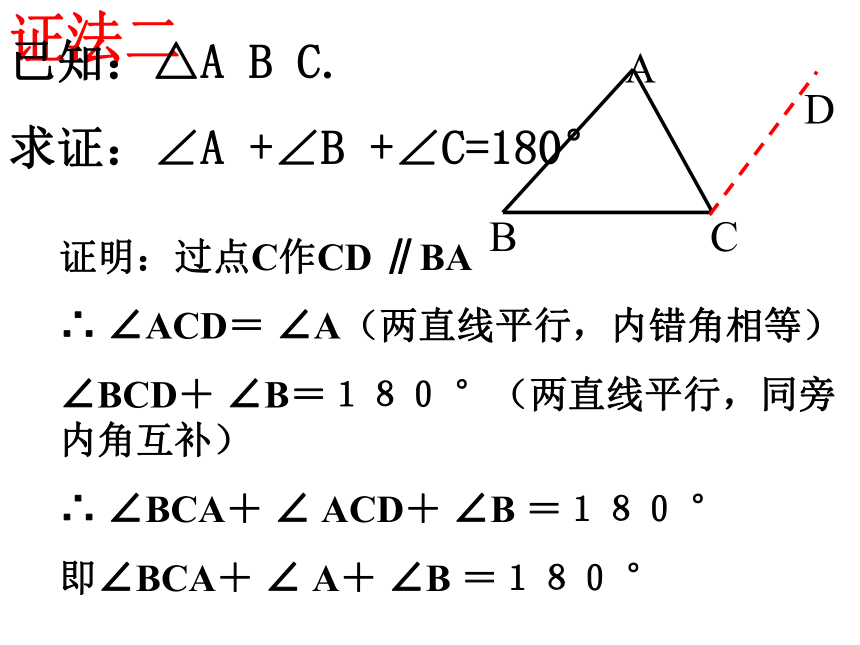
证法二
已知:△A B C.
求证:∠A +∠B +∠C=180°
A
B
C
D
证明:过点C作CD ∥BA
∴ ∠ACD= ∠A(两直线平行,内错角相等)
∠BCD+ ∠B=180 °(两直线平行,同旁内角互补)
∴ ∠BCA+ ∠ ACD+ ∠B =180 °
即∠BCA+ ∠ A+ ∠B =180 °
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线。在平面几何里,辅助线通常画成虚线。
思路总结
为了证明三个角的和为1800,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.
一个完整的证明题应具备哪些部分
证明过程
已知求证
图形
(1)在△ABC中,∠A=35°,
∠ B=43 °则∠C= .
(2)在△ABC中∠A :∠B:∠C
=2:3:4则∠A = ∠ B= ∠ C= .
1、 (1)一个三角形中最多有 个直角? 为什么?
(2)一个三角形中最多有 个钝角? 为什么?
(3)一个三角形中至少有 个锐角?为什么?
(4)任意 一个三角形中,最大的一个角的度数至少为 .
当堂训练
2、已知:三角形三个内角的度数之比为1:3:5,求这三个内角的度数。
解:设三个内角度数分别为:x、3x、5x,
x+3x+5x=180°
解得 x=20°
所以三个内角度数分别为 :20°,60°,100°。
由三角形内角和为180°得
当堂训练 小试牛刀
方程思想在数学计算中地位显著
解:在△ACD中 ∠CAD =30 ° ∠D =90 °
D
A
B
C
∴ ∠ACD =180 ° -30 ° -90 °=6 0 °
在△BCD中 ∠CBD = 45 ° ∠D =90 °
∴ ∠BCD = 180 °- 90°-45 °=45 °
∴ ∠ACB = ∠ACD - ∠BCD = 6 0 °- 45 °=150
3、如图,从A处观测C处时∠CAD=30°,从B处观测C处时∠CBD=45°.从C处观测A、B两处∠ACB是多少?
当堂训练 小试牛刀
A
B
C
D
E
北
北
4、如图,C岛在A岛的北偏东50°方向
B岛在A岛的北偏东80 °方
向,C岛在B岛的北偏西
40 °方向,从C岛看A、B
两岛的视角∠ACB是多少度?
.△A B C中,∠A =∠B +∠C,问△A B C是什么三角形?
. △A B C 中,∠C =2 (∠B+∠A ),求∠C 的度数。
5.在△ABC中:
①∠A=35°, ∠C=90 °,则∠B=?
②∠A=50°,∠B=∠C,则∠B=?
③ ∠A : ∠B :∠C=3:2:1,问 △ABC
是什么三角形?
④ ∠A -∠C =35 °,∠B -∠C =10 °, 则∠B =?
1、一个三角形最多有 个直角,
最多有 个钝角。
2、在△ABC中,若∠A+∠B=2∠C,则∠C= 。
3、若一个三角形的三个内角之比为2:3:4,
则这三个内角的度数为 。
1
1
600
400,600,800
完全达标检测:
A
B
C
D
F
4.如图,AF、AD分别是△ ABC的高
和角平分线,且∠B=36 ° ,
∠C=76 °求∠DAF的度数。
解:在△ABC中,
∠BAC + ∠ B+ ∠ C=180
∵ ∠B=36 ° , ∠C=76 °
课堂小结:
1.三角形内角和定理及其的证明。
2.三角形内角和定理与推论的运用。
3明确一个完整的证明题是由已知求证、图形、证明过程三部分组成;
4三角形内角和的定理证明中,添加辅助线的实质是通过平行线来移动角。
习题1、2①②、3、4、7
布置作业:
2、明确一个完整的证明题是由哪些部分组成;提高学生用数学语言叙述问题的意识和能力。
3、经历添加辅助线的过程,帮助学生树立解题遇到困难时添加辅助线的意识。
4、经历动手实验得到结论,激发学生学习数学的兴趣。
揭示目标:
预习检测:
1、三角形的内角和定理:
三角形三个内角的和是180 °
即:如图:在△ABC中,
∠A +∠B +∠C=180 °
A
B
C
三角形的三个内角和是多少?如何用数学语言叙述这个定理
把三个角拼在一起试试看?
从刚才拼角的过程你能想出证明的办法吗?
结论:三角形的内角和等于180 °
已知:△A B C.
求证:∠A +∠B +∠C =180°
A.
B
C
B.
E
证明:过A 作E F∥B C.
∴ ∠E A B =∠B.∠F A C = ∠C
﹙两直线平行,内错角相等﹚
∵∠E A B +∠B A C +∠C A F =180°
∴ ∠B +∠B A C +∠C= 180° ﹙ 等量代换﹚
F
已知:△A B C.
求证:∠A +∠B +∠C =180°
A
B
C
证法二
已知:△A B C.
求证:∠A +∠B +∠C=180°
A
B
C
D
证明:过点C作CD ∥BA
∴ ∠ACD= ∠A(两直线平行,内错角相等)
∠BCD+ ∠B=180 °(两直线平行,同旁内角互补)
∴ ∠BCA+ ∠ ACD+ ∠B =180 °
即∠BCA+ ∠ A+ ∠B =180 °
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线。在平面几何里,辅助线通常画成虚线。
思路总结
为了证明三个角的和为1800,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.
一个完整的证明题应具备哪些部分
证明过程
已知求证
图形
(1)在△ABC中,∠A=35°,
∠ B=43 °则∠C= .
(2)在△ABC中∠A :∠B:∠C
=2:3:4则∠A = ∠ B= ∠ C= .
1、 (1)一个三角形中最多有 个直角? 为什么?
(2)一个三角形中最多有 个钝角? 为什么?
(3)一个三角形中至少有 个锐角?为什么?
(4)任意 一个三角形中,最大的一个角的度数至少为 .
当堂训练
2、已知:三角形三个内角的度数之比为1:3:5,求这三个内角的度数。
解:设三个内角度数分别为:x、3x、5x,
x+3x+5x=180°
解得 x=20°
所以三个内角度数分别为 :20°,60°,100°。
由三角形内角和为180°得
当堂训练 小试牛刀
方程思想在数学计算中地位显著
解:在△ACD中 ∠CAD =30 ° ∠D =90 °
D
A
B
C
∴ ∠ACD =180 ° -30 ° -90 °=6 0 °
在△BCD中 ∠CBD = 45 ° ∠D =90 °
∴ ∠BCD = 180 °- 90°-45 °=45 °
∴ ∠ACB = ∠ACD - ∠BCD = 6 0 °- 45 °=150
3、如图,从A处观测C处时∠CAD=30°,从B处观测C处时∠CBD=45°.从C处观测A、B两处∠ACB是多少?
当堂训练 小试牛刀
A
B
C
D
E
北
北
4、如图,C岛在A岛的北偏东50°方向
B岛在A岛的北偏东80 °方
向,C岛在B岛的北偏西
40 °方向,从C岛看A、B
两岛的视角∠ACB是多少度?
.△A B C中,∠A =∠B +∠C,问△A B C是什么三角形?
. △A B C 中,∠C =2 (∠B+∠A ),求∠C 的度数。
5.在△ABC中:
①∠A=35°, ∠C=90 °,则∠B=?
②∠A=50°,∠B=∠C,则∠B=?
③ ∠A : ∠B :∠C=3:2:1,问 △ABC
是什么三角形?
④ ∠A -∠C =35 °,∠B -∠C =10 °, 则∠B =?
1、一个三角形最多有 个直角,
最多有 个钝角。
2、在△ABC中,若∠A+∠B=2∠C,则∠C= 。
3、若一个三角形的三个内角之比为2:3:4,
则这三个内角的度数为 。
1
1
600
400,600,800
完全达标检测:
A
B
C
D
F
4.如图,AF、AD分别是△ ABC的高
和角平分线,且∠B=36 ° ,
∠C=76 °求∠DAF的度数。
解:在△ABC中,
∠BAC + ∠ B+ ∠ C=180
∵ ∠B=36 ° , ∠C=76 °
课堂小结:
1.三角形内角和定理及其的证明。
2.三角形内角和定理与推论的运用。
3明确一个完整的证明题是由已知求证、图形、证明过程三部分组成;
4三角形内角和的定理证明中,添加辅助线的实质是通过平行线来移动角。
习题1、2①②、3、4、7
布置作业:
