人教版数学八年级上册第十一章 三角形复习课件(共34张PPT)
文档属性
| 名称 | 人教版数学八年级上册第十一章 三角形复习课件(共34张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 600.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-25 16:11:32 | ||
图片预览







文档简介
三角形
会说出并应用以下知识点:
1、三角形的概念及三角形的边角关系.
2、三角形中的重要线段及三角形的分类.
3、全等的图形、三角形全等的条件及全等三角形的特征.
4、尺规作图的意义,画三角形的基本方法.
5、应用三角形的有关知识解决某些简单的测量问题.
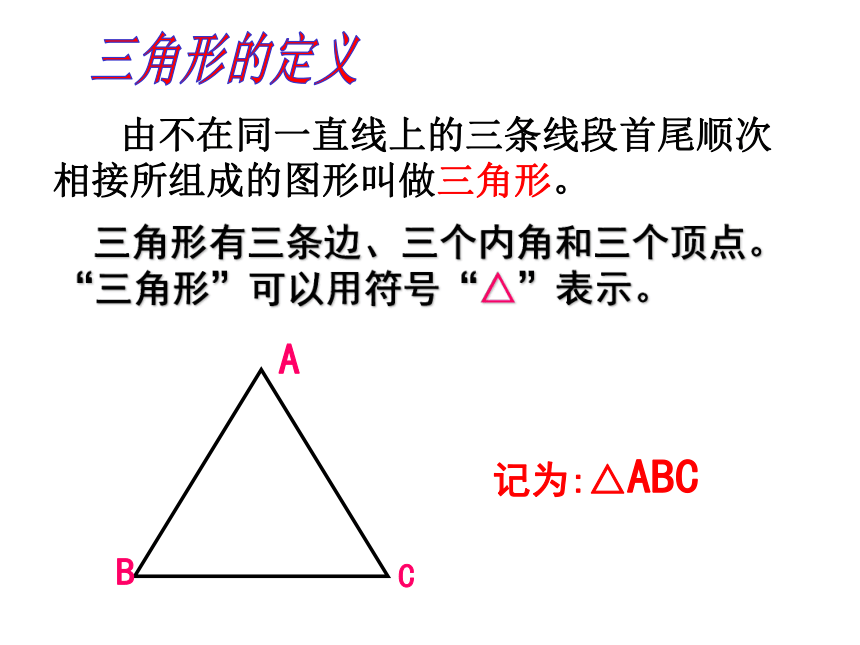
由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
A
B
C
记为:△ABC
三角形有三条边、三个内角和三个顶点。
“三角形”可以用符号“△”表示。
1、三角形任意两边之和大于第三边。
2、三角形任意两边之差小于第三边。
3、三角形三个内角的和等于180度。
4、直角三角形的两个锐角互余。
5、三角形的三条角平分线交于一点,
三条中线交于一点。
6、三角形的三条高所在的直线交于一点。
7、全等图形的形状和大小都相同。(两三角形完全重合)
8、全等三角形的对应边相等,对应角相等。
三角形
三角形
的边
三角形
的角
三角形
的线段
三角形的全等
全等性质
全等条件
SSS
SAS
ASA
AAS
HL
1、两个能够重合的三角形称为全等三角形。
SSS SAS ASA AAS HL
SSS SAS(两边夹角) ASA (两角夹边) AAS
2、两个三角形全等的条件:
3、两个直角三角形全等的条件:
1、三角形两条边分别是2cm,7cm,则第三边c的范围为 。
2、等腰三角形的一边长为6cm,另一边长为12cm,则其周长( )
A、24cm B、30cm
C、24cM或30cm D、18cm
3、用7根火柴首尾顺次连结摆成一个三角形,能摆成不同的三角形的个数为 。
5<c<9
B
2
(3,3,1;2,2,3)
x
3x
5x
1、如图,求△ABC各内角的度数。
2、已知三角形三个内角的度数比为1:3:5,求这三个内角的度数。
解:3x + 2x + x = 180
6x=180 X=30
∴三角形各内角的度数分别为:30°,60°,90°
解:设三个内角分别为x,3x,5x
则x + 3x + 5x = 180 x=20
∴三角形三个内角分别为:20°,60°,100°
2x
3x
x
A
B
C
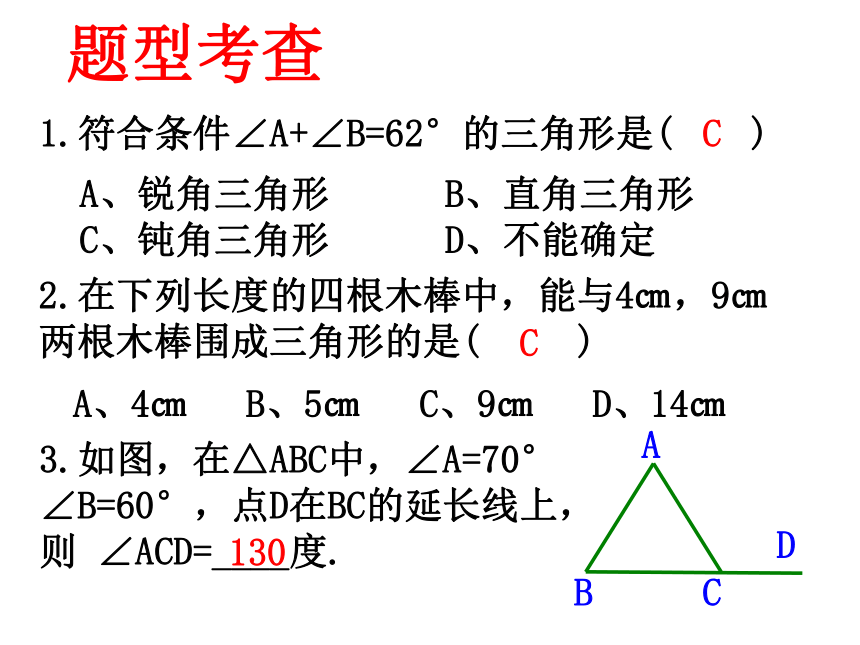
1.符合条件∠A+∠B=62°的三角形是( )
A、4㎝ B、5㎝ C、9㎝ D、14㎝
C
3.如图,在△ABC中,∠A=70° ∠B=60°,点D在BC的延长线上,则 ∠ACD=____度.
130
A
B
C
D
2.在下列长度的四根木棒中,能与4㎝,9㎝两根木棒围成三角形的是( )
A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定
C
题型考查
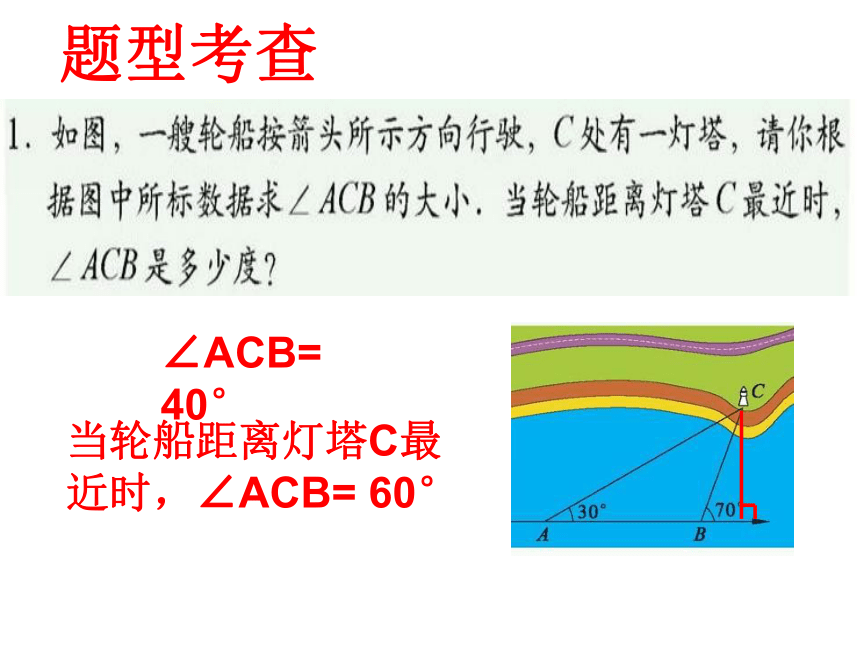
题型考查
∠ACB= 40°
当轮船距离灯塔C最近时,∠ACB= 60°
1、在△ABC中,已知∠A=30°,∠B=70°,则∠C的度数是 。
2、在Rt△ABC中,一个锐角为30°,则另一个锐角为 度。
3、按三角形内角的大小可以把三角形分为: 三角形、 三角形、 三角形。
4、已知一个三角形的三条边长为2、7、x,则x 的取值范围是 。
5、等腰三角形一边的长是4,另一边的长是8,则它的周长是 。
学习考查
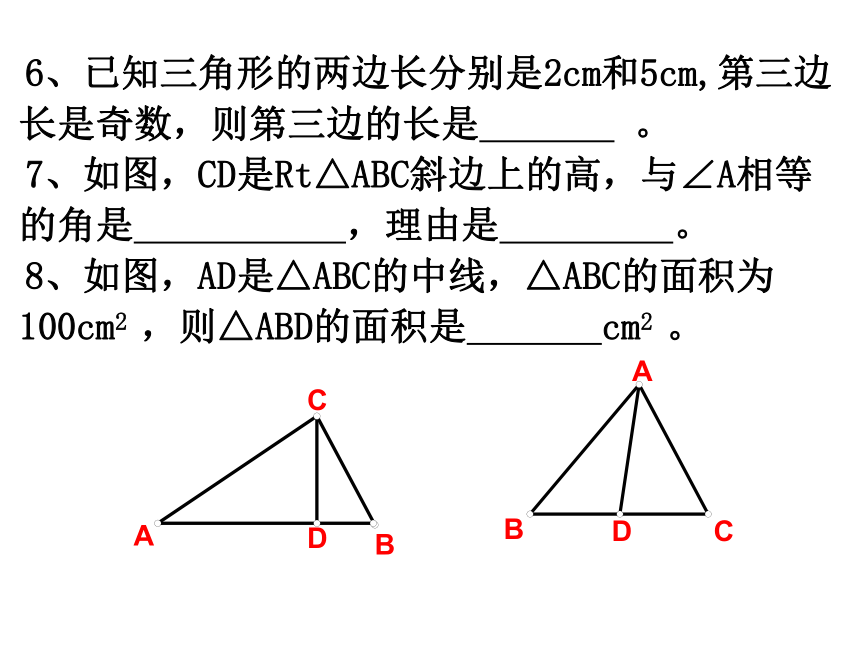
6、已知三角形的两边长分别是2cm和5cm,第三边长是奇数,则第三边的长是 。
7、如图,CD是Rt△ABC斜边上的高,与∠A相等的角是 ,理由是 。
8、如图,AD是△ABC的中线,△ABC的面积为100cm2 ,则△ABD的面积是 cm2 。
A
B
C
D
A
B
C
D
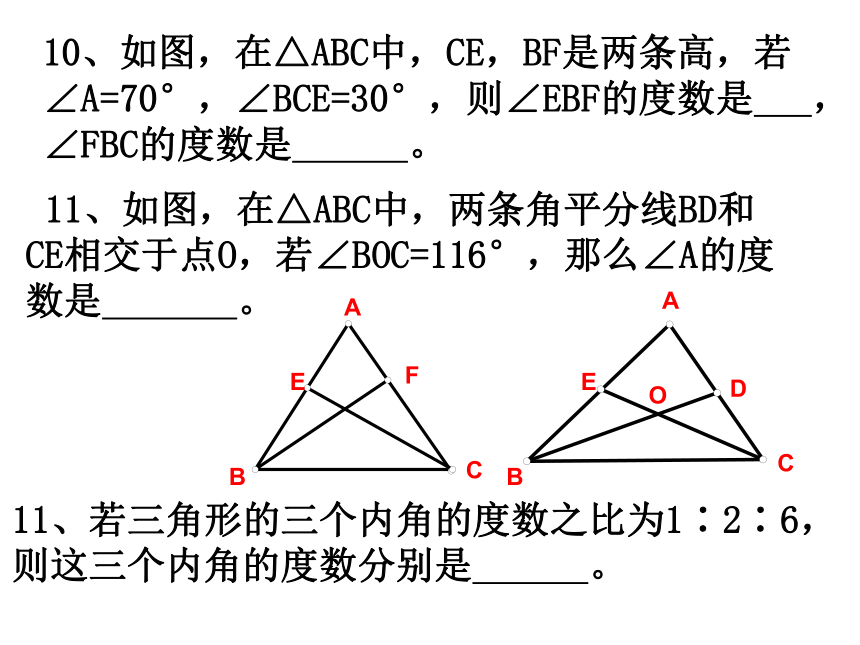
10、如图,在△ABC中,CE,BF是两条高,若∠A=70°,∠BCE=30°,则∠EBF的度数是 ,∠FBC的度数是 。
11、如图,在△ABC中,两条角平分线BD和CE相交于点O,若∠BOC=116°,那么∠A的度数是 。
A
B
C
E
F
A
B
C
D
E
O
11、若三角形的三个内角的度数之比为1∶2∶6,则这三个内角的度数分别是 。
1、下列各组数中不可能是一个三角形的边长的是( )
A 、5,12,13 B、5,7,7 C 、5,7,12 D、101,102,103
2、三角形中至少有一个角大于或等于( )
A、45° B、55° C、60° D、65°
3、如果直角三角形的一个锐角是另一个锐角的4倍,那么这个直角三角形中一个锐角的度数是( )
A、9° B、18° C、27° D、36°
学习考查
4、下列说法正确的是( )
A 两个周长相等的长方形全等
B 两个周长相等的三角形全等
C 两个面积相等的长方形全等
D 两个周长相等的圆全等
5、判定两个三角形全等,给出如下四组条件: ①两边和一角对应相等;②两角和一边对应相等; ③两个直角三角形中斜边和一条直角边对应相等;④三个角对应相等;其中能判定这两个三角形全等的条件是( )
A、①和② B、 ①和④
C、②和③ D、③和④
1、如图AB=CD,AC=BD,则△ABC≌△DCB吗?说明理由。
解:△ABC≌△DCB
在△ABC与△DCB中
∵ AB=CD(已知)
AC=BD (已知)
BC=CB(公共边)
∴△ABC≌△DCB(SSS)
{
A
B
C
D
1、已知:如图 ∠ABC=∠DCB, AB=DC,
求证: (1)AC=BD; (2)S△AOB = S△DOC
A
B
D
C
O
变式训练
A
B
D
C
O
2、如图,已知∠ABC=∠DCB,要使△ABC≌△DCB,只需添加一个条件是 _____________。(只需添加一个你认为适合的条件)
AB=DC
∠A=∠D
∠1=∠2
1
2
隐含条件:BC=CB
SAS
AAS
ASA
2.已知:∠B=∠DEF,BC=EF,现要证明△ABC≌△DEF,
若要以“SAS”为依据,还缺条件______;
若要以“ASA”为依据,还缺条件______ _;
若要以“AAS”为依据,还缺条件_______,
并说明理由.
AB=DE
∠ACB=∠F
∠A=∠D
已知条件:
∠B=∠DEF,
BC=EF
A
B
C
D
E
F
在△ABC与△ADC中
∵ ∠1=∠2(已知)
∠B=∠D(已知)
AC=AC(公共边)
∴ △ABC≌△ADC(AAS)
3、已知:如图,∠1=∠2,∠B=∠D。
求证:△ABC≌△ADC
A
B
C
D
1
2
4、如图,已知AB=AC,BD=CE。
求证:△ABE≌△ACD。
在△ABE与△ACD中
∵ AB=AC(已知)
AD=AE(已证)
∠A=∠A(公共角)
∴ △ABE≌△ACD(SAS)
证明:∵ AB=AC,BD=CE(已知)
∴AD=AE(等式性质)
B
A
C
D
E
5、如图,AB,CD交于点E,且AE=DE,EC=EB,试说明:BD=AC
解:在△AEC与△DEB中
∵ AE=DE(已知)
EC=EB已知)
∠BED=∠CEA(对顶角相等)
∴ △AEC≌△DEB(SAS)
∴ BD=AC(全等三角形的对应边相等)
A
B
C
D
E
补充练习:
D
C
B
A
1、在△ABC中,AB=AC,AD是边BC上的中线,证明:∠BAD=∠CAD
证明:∵AD是BC边上的中线
∴BD=CD(三角形中线的定义)
在△ABD和△ACD中
∴ △ABD≌△ACD(SSS)
∴ ∠BAD=∠CAB(全等三角形对应角相等)
解: △ABC和△ADE全等。 ∵∠1=∠2(已知) ∴∠1+∠DAC=∠2+∠DAC 即∠BAC=∠DAE 在△ABC和△ADC 中
A
B
C
D
E
1
2
2.如图,已知∠C=∠E,∠1=∠2,AB=AD,△ABC和△ADE全等吗?为什么?
∴ △ABC≌△ADE
(AAS)
B
C
D
E
A
3、如图:已知AB=AC,∠B=∠C,△ABD与△ACE全等吗?为什么?
∴△ABD≌△ACE(ASA)
B
C
D
E
A
如图,已知AB=AC,AD=AE。∠B与∠C是否相等?
解:在△ABD和△ACE中
∴△ABD≌△ACE(SAS)
∴∠B=∠C(全等三角形对应角相等)
如图线段AB是一个池塘的长,现在想测量这个池塘的长度,在水上测量不方便,你有什么好的方法较方便地把池塘的长度测量出来吗?想想看。
B
A
小莉的设计方案:先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结CD,用米尺测出DE的长,这个长度就等于A,B两点的距离。请你说明理由。
AC=DC?
∠ACB=∠DCE
BC=EC
△ACB≌△DCE(SAS)
AB=DE
E
C
B
A
D
解:
B
C
D
E
A
如图,已知AB=AC,AD=AE。
求证:∠B=∠C
B
A
D
C
E
A
证明:在△ABD和△ACE中
∴△ABD≌△ACE(SAS)
∴∠B=∠C(全等三角形
对应角相等)
AC∥FD吗?为什么?
如图,∠B=∠E,AB=EF,BD=EC,那么△ABC与 △FED全等吗?为什么?
F
E
D
C
B
A
4
3
2
1
思考练习
1.如图,已知AC=BD,AD=BC,则△ABC和△BAD全等吗?说明理由。
A
B
C
D
2.如图,已知O是AB的中点,∠A= ∠B,则△AOC和△BOD全等吗?为什么?
A
O
B
C
D
3.如图, ∠1= ∠2 ,∠C= ∠D,那么AC=AD吗?
4.如图,已知AC=AD,AB平分∠CAD,试说明△ABC≌△ABD.
A
1
B
C
D
2
A
1
B
C
D
2
中考点睛
1.如图,线段AC与BD交于点O,且OA=OC,请添加一个条件,使△AOB≌△COD,这个条件是____。
A
B
C
D
O
答案:OD=OB,
或∠C=∠A,
或DC∥AB。
注:答案不唯一。
2.如图,E是BC的中点,∠1=∠2,AE=DE,试求AB=DC。
1
2
A
B
C
D
E
简解:∵E是BC的中点,∴BE=EC。又∴ ∠1=∠2,AE=DE,△ABE≌△DCE(SAS),∴AB=DC。
3.如图,已知BE⊥AD,CF⊥AD,且BE=CF,请你判断AD是△ABC的中线还是角平分线?请说明你判断的理由。
简解:∵BE=EC。∠BDE=∠CDF,BE=CF,△BDE≌△CDF(AAS),∴BD=CD。
A
B
C
D
E
F
会说出并应用以下知识点:
1、三角形的概念及三角形的边角关系.
2、三角形中的重要线段及三角形的分类.
3、全等的图形、三角形全等的条件及全等三角形的特征.
4、尺规作图的意义,画三角形的基本方法.
5、应用三角形的有关知识解决某些简单的测量问题.
由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
A
B
C
记为:△ABC
三角形有三条边、三个内角和三个顶点。
“三角形”可以用符号“△”表示。
1、三角形任意两边之和大于第三边。
2、三角形任意两边之差小于第三边。
3、三角形三个内角的和等于180度。
4、直角三角形的两个锐角互余。
5、三角形的三条角平分线交于一点,
三条中线交于一点。
6、三角形的三条高所在的直线交于一点。
7、全等图形的形状和大小都相同。(两三角形完全重合)
8、全等三角形的对应边相等,对应角相等。
三角形
三角形
的边
三角形
的角
三角形
的线段
三角形的全等
全等性质
全等条件
SSS
SAS
ASA
AAS
HL
1、两个能够重合的三角形称为全等三角形。
SSS SAS ASA AAS HL
SSS SAS(两边夹角) ASA (两角夹边) AAS
2、两个三角形全等的条件:
3、两个直角三角形全等的条件:
1、三角形两条边分别是2cm,7cm,则第三边c的范围为 。
2、等腰三角形的一边长为6cm,另一边长为12cm,则其周长( )
A、24cm B、30cm
C、24cM或30cm D、18cm
3、用7根火柴首尾顺次连结摆成一个三角形,能摆成不同的三角形的个数为 。
5<c<9
B
2
(3,3,1;2,2,3)
x
3x
5x
1、如图,求△ABC各内角的度数。
2、已知三角形三个内角的度数比为1:3:5,求这三个内角的度数。
解:3x + 2x + x = 180
6x=180 X=30
∴三角形各内角的度数分别为:30°,60°,90°
解:设三个内角分别为x,3x,5x
则x + 3x + 5x = 180 x=20
∴三角形三个内角分别为:20°,60°,100°
2x
3x
x
A
B
C
1.符合条件∠A+∠B=62°的三角形是( )
A、4㎝ B、5㎝ C、9㎝ D、14㎝
C
3.如图,在△ABC中,∠A=70° ∠B=60°,点D在BC的延长线上,则 ∠ACD=____度.
130
A
B
C
D
2.在下列长度的四根木棒中,能与4㎝,9㎝两根木棒围成三角形的是( )
A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定
C
题型考查
题型考查
∠ACB= 40°
当轮船距离灯塔C最近时,∠ACB= 60°
1、在△ABC中,已知∠A=30°,∠B=70°,则∠C的度数是 。
2、在Rt△ABC中,一个锐角为30°,则另一个锐角为 度。
3、按三角形内角的大小可以把三角形分为: 三角形、 三角形、 三角形。
4、已知一个三角形的三条边长为2、7、x,则x 的取值范围是 。
5、等腰三角形一边的长是4,另一边的长是8,则它的周长是 。
学习考查
6、已知三角形的两边长分别是2cm和5cm,第三边长是奇数,则第三边的长是 。
7、如图,CD是Rt△ABC斜边上的高,与∠A相等的角是 ,理由是 。
8、如图,AD是△ABC的中线,△ABC的面积为100cm2 ,则△ABD的面积是 cm2 。
A
B
C
D
A
B
C
D
10、如图,在△ABC中,CE,BF是两条高,若∠A=70°,∠BCE=30°,则∠EBF的度数是 ,∠FBC的度数是 。
11、如图,在△ABC中,两条角平分线BD和CE相交于点O,若∠BOC=116°,那么∠A的度数是 。
A
B
C
E
F
A
B
C
D
E
O
11、若三角形的三个内角的度数之比为1∶2∶6,则这三个内角的度数分别是 。
1、下列各组数中不可能是一个三角形的边长的是( )
A 、5,12,13 B、5,7,7 C 、5,7,12 D、101,102,103
2、三角形中至少有一个角大于或等于( )
A、45° B、55° C、60° D、65°
3、如果直角三角形的一个锐角是另一个锐角的4倍,那么这个直角三角形中一个锐角的度数是( )
A、9° B、18° C、27° D、36°
学习考查
4、下列说法正确的是( )
A 两个周长相等的长方形全等
B 两个周长相等的三角形全等
C 两个面积相等的长方形全等
D 两个周长相等的圆全等
5、判定两个三角形全等,给出如下四组条件: ①两边和一角对应相等;②两角和一边对应相等; ③两个直角三角形中斜边和一条直角边对应相等;④三个角对应相等;其中能判定这两个三角形全等的条件是( )
A、①和② B、 ①和④
C、②和③ D、③和④
1、如图AB=CD,AC=BD,则△ABC≌△DCB吗?说明理由。
解:△ABC≌△DCB
在△ABC与△DCB中
∵ AB=CD(已知)
AC=BD (已知)
BC=CB(公共边)
∴△ABC≌△DCB(SSS)
{
A
B
C
D
1、已知:如图 ∠ABC=∠DCB, AB=DC,
求证: (1)AC=BD; (2)S△AOB = S△DOC
A
B
D
C
O
变式训练
A
B
D
C
O
2、如图,已知∠ABC=∠DCB,要使△ABC≌△DCB,只需添加一个条件是 _____________。(只需添加一个你认为适合的条件)
AB=DC
∠A=∠D
∠1=∠2
1
2
隐含条件:BC=CB
SAS
AAS
ASA
2.已知:∠B=∠DEF,BC=EF,现要证明△ABC≌△DEF,
若要以“SAS”为依据,还缺条件______;
若要以“ASA”为依据,还缺条件______ _;
若要以“AAS”为依据,还缺条件_______,
并说明理由.
AB=DE
∠ACB=∠F
∠A=∠D
已知条件:
∠B=∠DEF,
BC=EF
A
B
C
D
E
F
在△ABC与△ADC中
∵ ∠1=∠2(已知)
∠B=∠D(已知)
AC=AC(公共边)
∴ △ABC≌△ADC(AAS)
3、已知:如图,∠1=∠2,∠B=∠D。
求证:△ABC≌△ADC
A
B
C
D
1
2
4、如图,已知AB=AC,BD=CE。
求证:△ABE≌△ACD。
在△ABE与△ACD中
∵ AB=AC(已知)
AD=AE(已证)
∠A=∠A(公共角)
∴ △ABE≌△ACD(SAS)
证明:∵ AB=AC,BD=CE(已知)
∴AD=AE(等式性质)
B
A
C
D
E
5、如图,AB,CD交于点E,且AE=DE,EC=EB,试说明:BD=AC
解:在△AEC与△DEB中
∵ AE=DE(已知)
EC=EB已知)
∠BED=∠CEA(对顶角相等)
∴ △AEC≌△DEB(SAS)
∴ BD=AC(全等三角形的对应边相等)
A
B
C
D
E
补充练习:
D
C
B
A
1、在△ABC中,AB=AC,AD是边BC上的中线,证明:∠BAD=∠CAD
证明:∵AD是BC边上的中线
∴BD=CD(三角形中线的定义)
在△ABD和△ACD中
∴ △ABD≌△ACD(SSS)
∴ ∠BAD=∠CAB(全等三角形对应角相等)
解: △ABC和△ADE全等。 ∵∠1=∠2(已知) ∴∠1+∠DAC=∠2+∠DAC 即∠BAC=∠DAE 在△ABC和△ADC 中
A
B
C
D
E
1
2
2.如图,已知∠C=∠E,∠1=∠2,AB=AD,△ABC和△ADE全等吗?为什么?
∴ △ABC≌△ADE
(AAS)
B
C
D
E
A
3、如图:已知AB=AC,∠B=∠C,△ABD与△ACE全等吗?为什么?
∴△ABD≌△ACE(ASA)
B
C
D
E
A
如图,已知AB=AC,AD=AE。∠B与∠C是否相等?
解:在△ABD和△ACE中
∴△ABD≌△ACE(SAS)
∴∠B=∠C(全等三角形对应角相等)
如图线段AB是一个池塘的长,现在想测量这个池塘的长度,在水上测量不方便,你有什么好的方法较方便地把池塘的长度测量出来吗?想想看。
B
A
小莉的设计方案:先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结CD,用米尺测出DE的长,这个长度就等于A,B两点的距离。请你说明理由。
AC=DC?
∠ACB=∠DCE
BC=EC
△ACB≌△DCE(SAS)
AB=DE
E
C
B
A
D
解:
B
C
D
E
A
如图,已知AB=AC,AD=AE。
求证:∠B=∠C
B
A
D
C
E
A
证明:在△ABD和△ACE中
∴△ABD≌△ACE(SAS)
∴∠B=∠C(全等三角形
对应角相等)
AC∥FD吗?为什么?
如图,∠B=∠E,AB=EF,BD=EC,那么△ABC与 △FED全等吗?为什么?
F
E
D
C
B
A
4
3
2
1
思考练习
1.如图,已知AC=BD,AD=BC,则△ABC和△BAD全等吗?说明理由。
A
B
C
D
2.如图,已知O是AB的中点,∠A= ∠B,则△AOC和△BOD全等吗?为什么?
A
O
B
C
D
3.如图, ∠1= ∠2 ,∠C= ∠D,那么AC=AD吗?
4.如图,已知AC=AD,AB平分∠CAD,试说明△ABC≌△ABD.
A
1
B
C
D
2
A
1
B
C
D
2
中考点睛
1.如图,线段AC与BD交于点O,且OA=OC,请添加一个条件,使△AOB≌△COD,这个条件是____。
A
B
C
D
O
答案:OD=OB,
或∠C=∠A,
或DC∥AB。
注:答案不唯一。
2.如图,E是BC的中点,∠1=∠2,AE=DE,试求AB=DC。
1
2
A
B
C
D
E
简解:∵E是BC的中点,∴BE=EC。又∴ ∠1=∠2,AE=DE,△ABE≌△DCE(SAS),∴AB=DC。
3.如图,已知BE⊥AD,CF⊥AD,且BE=CF,请你判断AD是△ABC的中线还是角平分线?请说明你判断的理由。
简解:∵BE=EC。∠BDE=∠CDF,BE=CF,△BDE≌△CDF(AAS),∴BD=CD。
A
B
C
D
E
F
