人教版数学八年级上册11.3.2多边形及其内角和课件(29张)
文档属性
| 名称 | 人教版数学八年级上册11.3.2多边形及其内角和课件(29张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 685.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-26 22:20:14 | ||
图片预览




文档简介
1、n边形的内角和等于__________,
九边形的内角和等于______________。
2、一个多边形的内角和等于1440°,那么它是___边形.
3、正五边形的每一个内角的度数是_____,每个外角度数为__。
4、从六边形的一个顶点出发可画_____条对角线,这些对角线把六边形分成_____个三角形。
一个六边形共有_____条对角线。
(n - 2) ? 180°
1260°
十
108°
三
四
9
预习检测
720
学习目标:
1.经历多边形的内角和与外角和的探究过程,掌握多边形的内角和与外角和,能运用它们进行计算与证明。
2.能运用多边形的内角和与外角和解决实际问题。
1、三角形的内角和是_____.
2、你能够利用三角形的内角和求四边形的内角和吗?试试看?
A
B
C
D
思路:多边形问题转化为三角形问题来解决.
四边形的内角和为3600
1800
问题引导下的再学习
A
C
B
如图,三角形ABC的内角和是多少度?
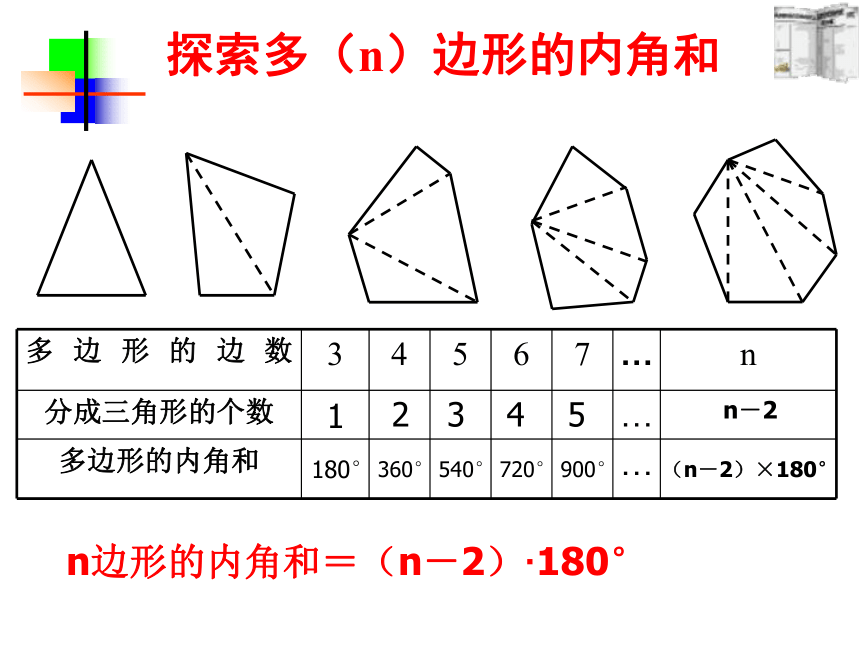
探索多边形的内角和
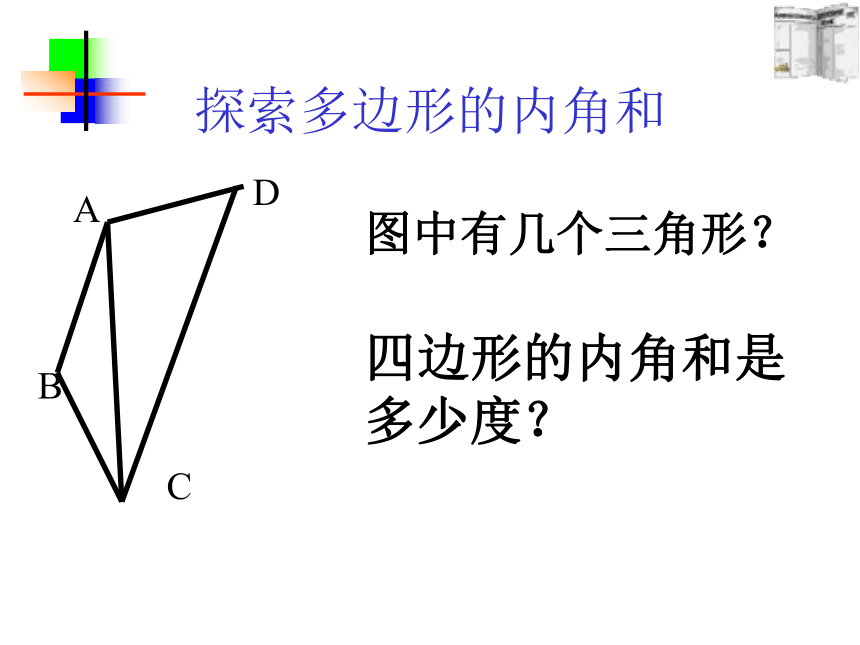
探索多边形的内角和
A
B
C
D
四边形的内角和是多少度?
图中有几个三角形?
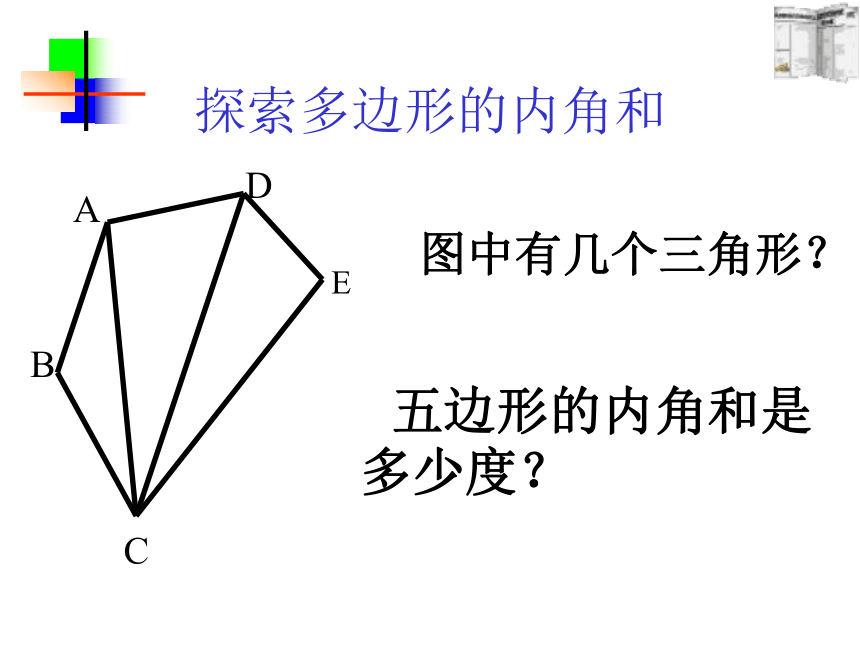
探索多边形的内角和
A
B
D
C
E
五边形的内角和是多少度?
图中有几个三角形?
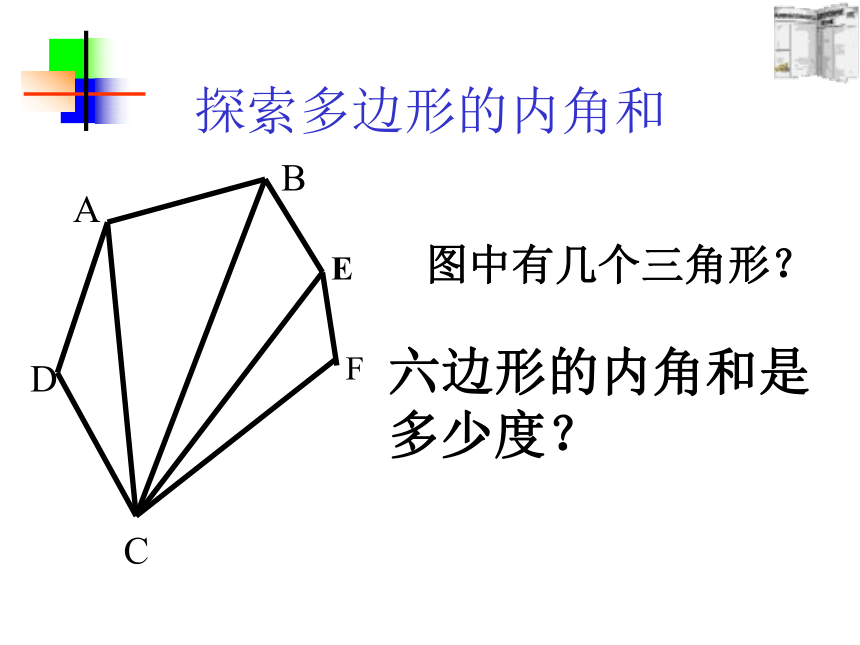
探索多边形的内角和
A
B
D
C
F
E
六边形的内角和是多少度?
图中有几个三角形?
多边形的边数
3
4
5
6
7
…
n
分成三角形的个数
…
多边形的内角和
…
1
180°
2
3
4
5
360°
540°
720°
900°
n-2
(n-2)×180°
n边形的内角和=(n-2)·180°
探索多(n)边形的内角和
除了上述我们利用对角线,将一个多边形分割成几个三角形外,还有其它的分割方法吗?
想一想:
多了什么?如何处理?
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
这种分割方式,将多边形分成n-1个三角形,故所有三角形的内角和为(n-1)×180 °,边上一点周围所形成的平角不是多边形的内角,因此n边形的内角和为
(n-1)×180 °- 180 °= (n-2)×180 °
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
该图中n边形共有n个三角形,故所有三角形内角和为n×180 °,但每个图中都有一个以红圈圈住的点,它是一个圆周角360 °,因此n边形的内角和为
n×180 °- 360 °= (n-2)×180 °
多了什么?如何处理?
得到定理:
n边形的内角和等于(n-2)·180?.
说明:
(1)多边形的内角和仅与边数有关,与多边形的大小、形状无关;
(2)强调凸多边形的内角?的范围:0?结论:
例1:求八边形的内角和的度数。
解:(n-2)×180°=(8-2)×180°
=1080°
答:八边形的内角和为1080°。
例2:一个正多边形的一个内角为150°,
你知道它是几边形吗?
解:设 这个多边形为n边形,根据题意得:
(n-2)×180=150n
n=12
答:这个多边形是12边形。
另解:由于多边形外角和等于360°
而这个正多边形的每个外角都等于
180°-150°=30°,
所以这个正 多边形的边数等于
360°÷30°=12。
巩固练习:
3、多边形内角和为1080°则它是
( )边形。
4、多边形内角和为1800°则它是
( )边形。
1、七边形内角和为( )
2、十边形内角和为( )
5、有一个正多边形的外角是60°,那么该正多边形是正( )边形。
问题
大家清晨跑步吗?小明就有每天坚持跑步的好习惯,他怎样跑步呢?右图就是小明清晨沿一个五边形广场周围的小跑,按逆时针方向跑步的效果图. 请你观察并思考如下几个问题:
(1)小明每从一条街道转到下一条街道时,身体转过的角是哪个角?在图中标出它们.
A
B
C
D
E
1
2
3
4
5
(2)他每跑完一圈,身体转过的角度之和是多少?
(3)在上图中,你能求出1+∠2+∠3+∠4+∠5的大小吗?你是怎样得到的?
猜想与说理:
n边形的外角和是多少度呢?
答:都是360°.因为多边形的外角与它相邻的内角是邻补角,所以n边形的外角和加内角和等于n·180°,内角和为(n-2)·180°,因此,外角和为:n·180°-(n-2)·180°= 360°.
结论:多边形的外角和都等于360°.
探索:分别求出下列多边形的外角和的度数.
360°
360°
360°
360°
360°
例3:一个多边形的内角和等
于它的外角和的3倍,它
是几边形?
解:设它是n边形,则
(n-2).180=3×360
解得:n=8
答:它是8边形
例4:一个正多边形的每个内角比相邻外角大36°求这个多边形的边数。
解:设一个外角为x°,
则内角为(x+36)°
根据题意得:
x+x+36=180
x=72
360÷72=5
答:这个正多边形为正五边形。
1、一个十边形的每一个内角都相等,
那么这个十边形的每一外角等于( )
A、144° B、 72 ° C、 36° D 、18°
2、一个多边形每一个外角都等于45°,
则这个多边形的内角和等于( )
A、 720° B、 675° C、 1080°D、945°
C
C
巩固练习:
课堂练习:
1.一个多边形的外角都等于60°,这个多边形是n边形?
解:因为多边形的外角和等于360°,所以根据题意,可知道这个多边形的边数是:
360÷60=6 .答:这个多边形是六边形.
2.下图是三个完全相同的正多边形拼成的无缝隙不重叠的图形的一部分,这种多边形是几边形?为什么?
解:设:这个正多边形的一个内角为x°,
则由题图得:3x=360°. x=120°.
再根据多边形的内角和公式得:
n×120°=(n-2)×180°. 解得n=6 . 答:(略)
4、两个多边形的边数比是1:2,两个多边形的内角和为1440度,求这两个多边形的边数,
3、一个多边形的每个内角都比相邻的外角3倍多20度,求这个多边形的边数,
2、四边形的四个内角的比是8:6:3:7,求它的四个内角,
1、一个多边形的内角和是外角和的4倍,这是几边形
如图,四边形风筝的四个内角∠A、
∠B、∠C、∠D的度数之比为1∶1∶0.6∶1,
求它的四个内角的度数.
A
B
C
D
解∵ ∠A+∠B+∠C+∠D=360 ° (四边形的内角和等360 °)
又∵∠A,∠B,∠C,∠D的度数之比为1:1:0.6:1
设∠A=x度,则x+x+0.6x+x=360,
解得x=100.
∴∠A=∠B=∠D=100 °
∠C=100 °×0.6=60 °
1.已知四边形ABCD中, ∠A=80 °, ∠B=60°, ∠C=70°则∠D=_____.
2.已知四边形ABCD中, ∠A与∠C互补,∠B=80 °,则∠D= .
150 °
100°
3.四边形最多有_____个直角?最多有_____个钝角?
4
3
4. 如图,在四边形ABCD中, ∠A=85 °,∠D=110 °, ∠1的外角是71 °,则∠1=____,∠2=____.
B
85 °
A
D
C
110 °
2
71 °
1
1090
560
小结:
我们通过把多边形划分为若干个三角形,用三角形内角和去求多边形内角和,从而得到多边形的内角和公式为(n-2)× 180°。这种化未知为已知的转化方法,必须在学习中逐渐掌握。由于多边形外角和为360°,与边数无关,所以常把多边形内角和的问题转化为外角和来处理。
作 业:
课时练:21—22页达标检测,基础巩固。
鸟儿因为翅膀而飞翔
风筝因为风儿而飞翔
人类因为思考而飞翔
让我们一起想象,
让我们一起飞翔!
九边形的内角和等于______________。
2、一个多边形的内角和等于1440°,那么它是___边形.
3、正五边形的每一个内角的度数是_____,每个外角度数为__。
4、从六边形的一个顶点出发可画_____条对角线,这些对角线把六边形分成_____个三角形。
一个六边形共有_____条对角线。
(n - 2) ? 180°
1260°
十
108°
三
四
9
预习检测
720
学习目标:
1.经历多边形的内角和与外角和的探究过程,掌握多边形的内角和与外角和,能运用它们进行计算与证明。
2.能运用多边形的内角和与外角和解决实际问题。
1、三角形的内角和是_____.
2、你能够利用三角形的内角和求四边形的内角和吗?试试看?
A
B
C
D
思路:多边形问题转化为三角形问题来解决.
四边形的内角和为3600
1800
问题引导下的再学习
A
C
B
如图,三角形ABC的内角和是多少度?
探索多边形的内角和
探索多边形的内角和
A
B
C
D
四边形的内角和是多少度?
图中有几个三角形?
探索多边形的内角和
A
B
D
C
E
五边形的内角和是多少度?
图中有几个三角形?
探索多边形的内角和
A
B
D
C
F
E
六边形的内角和是多少度?
图中有几个三角形?
多边形的边数
3
4
5
6
7
…
n
分成三角形的个数
…
多边形的内角和
…
1
180°
2
3
4
5
360°
540°
720°
900°
n-2
(n-2)×180°
n边形的内角和=(n-2)·180°
探索多(n)边形的内角和
除了上述我们利用对角线,将一个多边形分割成几个三角形外,还有其它的分割方法吗?
想一想:
多了什么?如何处理?
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
这种分割方式,将多边形分成n-1个三角形,故所有三角形的内角和为(n-1)×180 °,边上一点周围所形成的平角不是多边形的内角,因此n边形的内角和为
(n-1)×180 °- 180 °= (n-2)×180 °
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
该图中n边形共有n个三角形,故所有三角形内角和为n×180 °,但每个图中都有一个以红圈圈住的点,它是一个圆周角360 °,因此n边形的内角和为
n×180 °- 360 °= (n-2)×180 °
多了什么?如何处理?
得到定理:
n边形的内角和等于(n-2)·180?.
说明:
(1)多边形的内角和仅与边数有关,与多边形的大小、形状无关;
(2)强调凸多边形的内角?的范围:0?结论:
例1:求八边形的内角和的度数。
解:(n-2)×180°=(8-2)×180°
=1080°
答:八边形的内角和为1080°。
例2:一个正多边形的一个内角为150°,
你知道它是几边形吗?
解:设 这个多边形为n边形,根据题意得:
(n-2)×180=150n
n=12
答:这个多边形是12边形。
另解:由于多边形外角和等于360°
而这个正多边形的每个外角都等于
180°-150°=30°,
所以这个正 多边形的边数等于
360°÷30°=12。
巩固练习:
3、多边形内角和为1080°则它是
( )边形。
4、多边形内角和为1800°则它是
( )边形。
1、七边形内角和为( )
2、十边形内角和为( )
5、有一个正多边形的外角是60°,那么该正多边形是正( )边形。
问题
大家清晨跑步吗?小明就有每天坚持跑步的好习惯,他怎样跑步呢?右图就是小明清晨沿一个五边形广场周围的小跑,按逆时针方向跑步的效果图. 请你观察并思考如下几个问题:
(1)小明每从一条街道转到下一条街道时,身体转过的角是哪个角?在图中标出它们.
A
B
C
D
E
1
2
3
4
5
(2)他每跑完一圈,身体转过的角度之和是多少?
(3)在上图中,你能求出1+∠2+∠3+∠4+∠5的大小吗?你是怎样得到的?
猜想与说理:
n边形的外角和是多少度呢?
答:都是360°.因为多边形的外角与它相邻的内角是邻补角,所以n边形的外角和加内角和等于n·180°,内角和为(n-2)·180°,因此,外角和为:n·180°-(n-2)·180°= 360°.
结论:多边形的外角和都等于360°.
探索:分别求出下列多边形的外角和的度数.
360°
360°
360°
360°
360°
例3:一个多边形的内角和等
于它的外角和的3倍,它
是几边形?
解:设它是n边形,则
(n-2).180=3×360
解得:n=8
答:它是8边形
例4:一个正多边形的每个内角比相邻外角大36°求这个多边形的边数。
解:设一个外角为x°,
则内角为(x+36)°
根据题意得:
x+x+36=180
x=72
360÷72=5
答:这个正多边形为正五边形。
1、一个十边形的每一个内角都相等,
那么这个十边形的每一外角等于( )
A、144° B、 72 ° C、 36° D 、18°
2、一个多边形每一个外角都等于45°,
则这个多边形的内角和等于( )
A、 720° B、 675° C、 1080°D、945°
C
C
巩固练习:
课堂练习:
1.一个多边形的外角都等于60°,这个多边形是n边形?
解:因为多边形的外角和等于360°,所以根据题意,可知道这个多边形的边数是:
360÷60=6 .答:这个多边形是六边形.
2.下图是三个完全相同的正多边形拼成的无缝隙不重叠的图形的一部分,这种多边形是几边形?为什么?
解:设:这个正多边形的一个内角为x°,
则由题图得:3x=360°. x=120°.
再根据多边形的内角和公式得:
n×120°=(n-2)×180°. 解得n=6 . 答:(略)
4、两个多边形的边数比是1:2,两个多边形的内角和为1440度,求这两个多边形的边数,
3、一个多边形的每个内角都比相邻的外角3倍多20度,求这个多边形的边数,
2、四边形的四个内角的比是8:6:3:7,求它的四个内角,
1、一个多边形的内角和是外角和的4倍,这是几边形
如图,四边形风筝的四个内角∠A、
∠B、∠C、∠D的度数之比为1∶1∶0.6∶1,
求它的四个内角的度数.
A
B
C
D
解∵ ∠A+∠B+∠C+∠D=360 ° (四边形的内角和等360 °)
又∵∠A,∠B,∠C,∠D的度数之比为1:1:0.6:1
设∠A=x度,则x+x+0.6x+x=360,
解得x=100.
∴∠A=∠B=∠D=100 °
∠C=100 °×0.6=60 °
1.已知四边形ABCD中, ∠A=80 °, ∠B=60°, ∠C=70°则∠D=_____.
2.已知四边形ABCD中, ∠A与∠C互补,∠B=80 °,则∠D= .
150 °
100°
3.四边形最多有_____个直角?最多有_____个钝角?
4
3
4. 如图,在四边形ABCD中, ∠A=85 °,∠D=110 °, ∠1的外角是71 °,则∠1=____,∠2=____.
B
85 °
A
D
C
110 °
2
71 °
1
1090
560
小结:
我们通过把多边形划分为若干个三角形,用三角形内角和去求多边形内角和,从而得到多边形的内角和公式为(n-2)× 180°。这种化未知为已知的转化方法,必须在学习中逐渐掌握。由于多边形外角和为360°,与边数无关,所以常把多边形内角和的问题转化为外角和来处理。
作 业:
课时练:21—22页达标检测,基础巩固。
鸟儿因为翅膀而飞翔
风筝因为风儿而飞翔
人类因为思考而飞翔
让我们一起想象,
让我们一起飞翔!
